Общее уравнение прямой у= кх+в. Найдём уравнение прямой проходящей через точки А и С. А(-1;-3) тогда -3=-к+в (просто подставляем вместо х (-1), а вместо у (-3)). Аналогично для С(5;2) 2=5к+в. Решаем систему
5=6к, к=5/6, в= -3+5/6=-2цел1/6
значит у=5/6х- 2цел1/6
Так как у точек В(3;5) и D(3;-5) абсциссы одинаковые, то уравнение прямой х=3
Подставим в первое уравнение х = 3 и найдём у
у=(5/6)*3 – 2цел1/6=15/6 – 13/6=2/6=1/3
Тогда точка пересечения диагоналей О(3;1/3)
В четырехугольнике с вершинами $%A(5,6), B(8,-1), C(-7,2), D(-1,8)$% найти точку пересечения диагоналей $%AC$% и $%BD$%.
Нашел координаты $%AC$% и $%BD$%, составил уравнения (исходя из того, что диагонали перпендикулярны). Подставив в первое точку $%C$%, а во второе точку $%D$% составил полные уравнения. Решил систему из двух уравнений и получил неверные ответы.
Может быть дело в том, что диагонали необязательно перпендикулярны и надо по-другому составлять уравнения?
задан 11 Июн ’12 8:41
AlexeyVorobyev
85 ● 2 ● 6 ● 13
100% принятых
Зачем попарно – не нужно это. Пусть p1,p2,p3,p4 – это точки с указанными координатами. Берем точку p1. Нужно найти какая из точек p2,p3,p4 является противоположной. Перебираем 3 варианта.Вариант 1. Строим прямую через p1 и p2. Определяем лежат ли точки p3 и p4 относительно этой прямой по разные стороны или по одну сторону. Если по разные стороны, то прямая через p1 и p2 и есть диагональ ! А раз это диагональ, то нужно построить вторую диагональ через p3 и p4. Потом найти их пересечение.Если у нас получилось что p3 или p4 лежит на прямой через p1 и p2, то это значит у нас кривой четырехугольник Если первый вариант не подошел, то перебираем два других варианта.Программу сам напиши.
- Найти точку О пересечения диагоналей четырехугольника АВСD, если известны координаты его вершин А В С D ( — 1 ; — 3) (3 ; 5) (5 ; 2) (3 ; — 5)?
- Отметьте на координатной плоскости точку А( — 1 ; 3) и точки M, N, P координаты которых равны или противоположны точке А?
- В параллелепипеде ABCDA1B1C1D1 вершины B( — 4 ; 2 ; 3) и D1(2 ; — 8 ; 1) Определите координаты точки пересечения его диагоналей ?
- 2. Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8)?
- По известным координатам трех вершин параллелограмма найти координаты четвертой вершины и точки пересечения диагоналей, если А(1 ; 0 ; 3), В(4 ; 5 ; 0), С(5 ; 4 ; 3)?
- Записать координаты вершин А, В, С параллелограмма ABCD, найти координаты вершины D и точки О (пересечения диагоналей параллелограмма)?
- Даны координаты двух вершин треугольника ( — 18, 14), (22, 34) и точки пересечения высот ( — 2, 10)?
- Найдите координаты вершины и координаты точки пересечения диагоналей параллелограмма АВСД А(0, 0, 0) В(1, 2, 3) С ( — 1, 1, — 2)?
- Постройте четырехугольник АВСD по координатам точек А( — 6 ; 2), В(6 ; 5), С1 ; — 3)D( — 7 ; 1)?
- ! СРОЧНО?
- В параллелограмме ABCD известны координаты точки пересечения диагоналей Е (1 ; — 2) и двух верршин А ( — 4 ; — 3) и В ( — 2 ; 5)?
- Четырехугольники
- теория по математике 📈 планиметрия
- Выпуклый четырехугольник
- Виды и свойства выпуклых четырехугольников
- Прямоугольник
- Квадрат
- Параллелограмм
- Трапеция
- Виды трапеций
- Средняя линия трапеции
- 🎥 Видео
Видео:Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать

Найти точку О пересечения диагоналей четырехугольника АВСD, если известны координаты его вершин А В С D ( — 1 ; — 3) (3 ; 5) (5 ; 2) (3 ; — 5)?
Математика | 10 — 11 классы
Найти точку О пересечения диагоналей четырехугольника АВСD, если известны координаты его вершин А В С D ( — 1 ; — 3) (3 ; 5) (5 ; 2) (3 ; — 5).
Общее уравнение прямой у = кх + в.
Найдём уравнение прямой проходящей через точки А и С.
А( — 1 ; — 3) тогда — 3 = — к + в (просто подставляем вместо х ( — 1), а вместо у ( — 3)).
Аналогично для С(5 ; 2) 2 = 5к + в.
Решаем систему — 3 = — к + в
2 = 5к + в Отсюда
5 = 6к, к = 5 / 6, в = — 3 + 5 / 6 = — 2цел1 / 6
значит у = 5 / 6х — 2цел1 / 6
Так как у точек В(3 ; 5) и D(3 ; — 5) абсциссы одинаковые, то уравнение прямой х = 3
Подставим в первое уравнение х = 3 и найдём у
у = (5 / 6) * 3 — 2цел1 / 6 = 15 / 6 — 13 / 6 = 2 / 6 = 1 / 3
Тогда точка пересечения диагоналей О(3 ; 1 / 3).
Видео:Уравнения стороны треугольника и медианыСкачать

Отметьте на координатной плоскости точку А( — 1 ; 3) и точки M, N, P координаты которых равны или противоположны точке А?
Отметьте на координатной плоскости точку А( — 1 ; 3) и точки M, N, P координаты которых равны или противоположны точке А.
Найдите координаты точки пересечения диагоналей четырехугольника AMNP.
Видео:Вычисляем высоту через координаты вершин 1Скачать

В параллелепипеде ABCDA1B1C1D1 вершины B( — 4 ; 2 ; 3) и D1(2 ; — 8 ; 1) Определите координаты точки пересечения его диагоналей ?
В параллелепипеде ABCDA1B1C1D1 вершины B( — 4 ; 2 ; 3) и D1(2 ; — 8 ; 1) Определите координаты точки пересечения его диагоналей ?
Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

2. Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8)?
2. Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8).
Докажите, что ABCD – прямоугольник, и найдите координаты точки пересечения его диагоналей.
Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

По известным координатам трех вершин параллелограмма найти координаты четвертой вершины и точки пересечения диагоналей, если А(1 ; 0 ; 3), В(4 ; 5 ; 0), С(5 ; 4 ; 3)?
По известным координатам трех вершин параллелограмма найти координаты четвертой вершины и точки пересечения диагоналей, если А(1 ; 0 ; 3), В(4 ; 5 ; 0), С(5 ; 4 ; 3).
Видео:Точка пересечения медиан в треугольникеСкачать

Записать координаты вершин А, В, С параллелограмма ABCD, найти координаты вершины D и точки О (пересечения диагоналей параллелограмма)?
Записать координаты вершин А, В, С параллелограмма ABCD, найти координаты вершины D и точки О (пересечения диагоналей параллелограмма).
Записать уравнение стороны АВ и высоты СН.
Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Даны координаты двух вершин треугольника ( — 18, 14), (22, 34) и точки пересечения высот ( — 2, 10)?
Даны координаты двух вершин треугольника ( — 18, 14), (22, 34) и точки пересечения высот ( — 2, 10).
Найти координаты третьей вершины треугольника.
Видео:Найти точку пересечения прямой и плоскостиСкачать

Найдите координаты вершины и координаты точки пересечения диагоналей параллелограмма АВСД А(0, 0, 0) В(1, 2, 3) С ( — 1, 1, — 2)?
Найдите координаты вершины и координаты точки пересечения диагоналей параллелограмма АВСД А(0, 0, 0) В(1, 2, 3) С ( — 1, 1, — 2).
Видео:Точка пересечения высот треугольника.Скачать

Постройте четырехугольник АВСD по координатам точек А( — 6 ; 2), В(6 ; 5), С1 ; — 3)D( — 7 ; 1)?
Постройте четырехугольник АВСD по координатам точек А( — 6 ; 2), В(6 ; 5), С1 ; — 3)D( — 7 ; 1).
Найдите координаты точки пересечения отрезков АС BD.
Видео:координаты центра тяжести треугольникаСкачать

! СРОЧНО?
В параллелограмме ABCD известны координаты точки пересечения диагоналей Е (1 ; — 2) и двух верршин А ( — 4 ; — 3) и В ( — 2 ; 5).
Найдите координаты двух других вершин параллелограмма.
Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать

В параллелограмме ABCD известны координаты точки пересечения диагоналей Е (1 ; — 2) и двух верршин А ( — 4 ; — 3) и В ( — 2 ; 5)?
В параллелограмме ABCD известны координаты точки пересечения диагоналей Е (1 ; — 2) и двух верршин А ( — 4 ; — 3) и В ( — 2 ; 5).
Найдите координаты двух других вершин параллелограмма.
На этой странице находится ответ на вопрос Найти точку О пересечения диагоналей четырехугольника АВСD, если известны координаты его вершин А В С D ( — 1 ; — 3) (3 ; 5) (5 ; 2) (3 ; — 5)?, из категории Математика, соответствующий программе для 10 — 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.
600 * 3 = 1800км пролетел 1 самолет за 3 часа 900 * 3 = 2700км пролетел 2 самолет за 3 часа 1800 + 2700 = 4500км расстояние между аэродромами 2способ 600 + 900 = 1500км / час общая скорость сближения 1500 * 3 = 4500км.
3 * 600 = 1800 км 3 * 900 = 2700 2700 + 1800 = 4500км.
1 2 4 8 16 делители числа 16.
2400 : 30 = 80 80 + 20 = 100 2400 : 100 = 24 30 — 24 = 6 Ответ : на 6 дней раньше срока.
X — стоимость тетради в линейку 8(х + 10) — 40 = 10х 8х + 80 — 40 = 10х 8х + 40 = 10х 2х = 40 х = 20 20 + 10 = 30(к) — тетрадь в клетку Ответ : тетрадь в линейку — 20 копеек, тетрадь в клетку — 30 копеек.
Числа относятся как 7 : 8 = > можно найти наименьшую часть, 7 + 8 = 15 45 / 15 = 3. Теперь можно найти сами числа : 3 * 7 = 21 3 * 8 = 24.
Второе третье и четвёртое.
Пусть 1 поле = а, второе б, тогда согласно условию составим уравнение а = 6b или a = b + 155 (а = 6b) = (a = b + 155) 6b = b + 155 5b = 155 b = 31 Следовательно на 2 луге 31ц, а на первом 31 + 155 = 186ц.
Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Четырехугольники
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
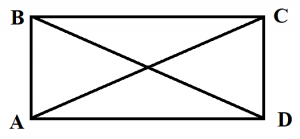
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Видео:Найти точку пересечения 3х плоскостейСкачать

Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.

- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
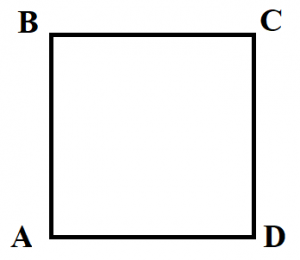
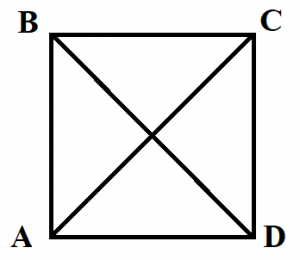
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб – это параллелограмм, у которого все стороны равны.
Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.
Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.
углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.
Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.
Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.
Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.
Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.
Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить
На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).
Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).
Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
🎥 Видео
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

8 класс, 37 урок, Теорема о пересечении высот треугольникаСкачать

Найди точку пересечения высот.Геометрия.Повторение.Скачать