Этот онлайн калькулятор позволит вам очень просто найти значение координат вектора по двум точкам (зная его начальную и конечную точку) для плоских и пространственных задач.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на определение координат вектора по двум точкам и закрепить пройденый материал.
- Калькулятор для вычисления координат вектора по двум точкам
- Инструкция использования калькулятора для вычисления координат вектора по двум точкам
- Ввод даных в калькулятор для вычисления координат вектора по двум точкам
- Дополнительные возможности калькулятора для вычисления координат вектора по двум точкам
- Теория. Координаты вектора по двум точкам
- Начертите попарно неколлинеарные векторы а, b и с. Постройте векторы: а) 2а + 3b — 4с; б) 1/2а-b + 1/3с.
- Ваш ответ
- решение вопроса
- Похожие вопросы
- 3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»
- 💥 Видео
Видео:Даны векторы a(1; 2), b( −3; 6) и c(4; -2). Найдите длину вектора a- b + с.Скачать

Калькулятор для вычисления координат вектора по двум точкам
Инструкция использования калькулятора для вычисления координат вектора по двум точкам
Ввод даных в калькулятор для вычисления координат вектора по двум точкам
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления координат вектора по двум точкам
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Видео:Вычитание векторов. 9 класс.Скачать

Теория. Координаты вектора по двум точкам
Например, вектор AB , заданный в пространстве координатами точек A(A x , A y , A z ) и B(B x , B y , B z ) можно найти использовав формулу:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Начертите попарно неколлинеарные векторы а, b и с. Постройте векторы: а) 2а + 3b — 4с; б) 1/2а-b + 1/3с.
Видео:ВЕКТОРЫ. Контрольная № 4 Геометрия 9 класс.Скачать

Ваш ответ
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

решение вопроса
Видео:Как построить точки в системе координат OXYZСкачать

Похожие вопросы
- Все категории
- экономические 43,280
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,971
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:№776. Начертите два неколлинеарных вектора х и у и постройте векторы: a) x+2y; б) ½y + х; в) 3x+½yСкачать

3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»
Даны векторы А = (-2; 3; 5) и B = (4; -1; 7). Найти координаты вектора
При умножении вектора на число все его координаты
Умножаются на это число, при сложении векторов складываются их соответствующие координаты.
Координаты коллинеарных векторов пропорциональны.
Если A || B, то 
Ответ: 
Найти направляющие косинусы вектора А = .
Направляющие косинусы являются координатами орта (единичного вектора) данного направления.
Найдем модуль вектора А:
Разделив все координаты вектора А на его модуль, получим координаты орта:
Ответ:
Тогда AA + BB + GC = <2A + B— 3G; —A + B+ G; 3A — B+ 2G>, причем координаты этого вектора должны равняться соответствующим координатам вектора D. Приравнивая эти координаты, получаем систему уравнений для определения A, B, G:
Для векторов A = , B = , C = , D = найти такие числа A, B, G, чтобы векторы AA, BB, GC и D образовали замкнутую ломаную линию, если начало каждого последующего вектора совместить с концом предыдущего.
C = линейно зависимой или линейно независимой.
Система векторов называется линейно независимой, если равенство
Вычислим главный определитель Δ системы уравнений
По правилу Крамера система имеет единственное решение, но для однородной системы всегда существует нулевое решение (A = B = G = 0).
Поскольку других решений нет, данная система векторов линейно независима.
Ответ: Система векторов линейно независима.
Найти координаты какого-либо вектора, направленного по биссектрисе угла между векторами А = (-4; 3; 0) и B = (12; -15; 16).
Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.
Вектор A + B направлен по диагонали параллелограмма, построенного на векторах А и B как на смежных сторонах и выходящей из общего начала векторов А и B.
Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.
Следовательно, |5A| = |B|. Значит, параллелограмм со сторонами, совпадающими с векторами 5A и B, является ромбом, поэтому вектор 5A + B будет иметь заданное направление.
При каких значениях X, Y, Z точки А(Х; -1; 3), В(5; -4; Z), C(-2; Y; 9), D(-5; 1; 7) являются вершинами параллелограмма?
Для выполнения условия задачи требуется коллинеарность векторов 



Для выполнения условия задачи требуется коллинеарность векторов 



Найдем координаты этих векторов:
Из последней пропорции получаем, что Z = 1 – 2Y. Тогда
Но при этих значениях неизвестных
Условие задачи выполнено.
Используйте определение скалярного произведения:
Используем свойства скалярного произведения:
По определению скалярного произведения
Сложим левые и правые части полученных равенств:
Даны векторы А = и B = . Найти скалярное произведение
Найдите координаты векторов 3А – B и A + 2B или используйте свойства скалярного произведения.
Используем свойства скалярного произведения:
Используйте формулу, выражающую косинус угла между векторами через их скалярное произведение.
Ответ: 
Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = <2K; -2K; 3K>.
Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = <2K; -2K; 3K>.
Известно, что |A| = 2, |B| = 7. Найти значения K, при которых векторы
Если векторы перпендикулярны, то их скалярное произведение равно нулю.
Если векторы перпендикулярны, то их скалярное произведение равно нулю.
Ответ: K = 
Найти проекцию вектора А = на ось, образующую с координатными осями Ох и Оу углы 60о и 45о, а с осью Oz – тупой угол γ.
Используйте свойство направляющих косинусов:
Найдем cosγ: cos260o + cos245o + cos2γ = 1,
Тогда проекция А на заданную ось равна:
💥 Видео
№925. Даны векторы а {2; 4}, b {-2; 0}, с {0; 0}, d {-2; -3}, е {2; -3}, fСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Умножение вектора на число. 9 класс.Скачать

Координаты вектора. 9 класс.Скачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Скалярное произведение векторов. 9 класс.Скачать

Сложение векторов. 9 класс.Скачать

№778. Начертите попарно неколлинеарные векторы а, b и c. Постройте векторы:Скачать

Координаты точки и координаты вектора 1.Скачать

№928. Даны векторы а {3; 7}, b {-2; 1}, с {6; 14}, d {2; -1}, е {2; 4}.Скачать

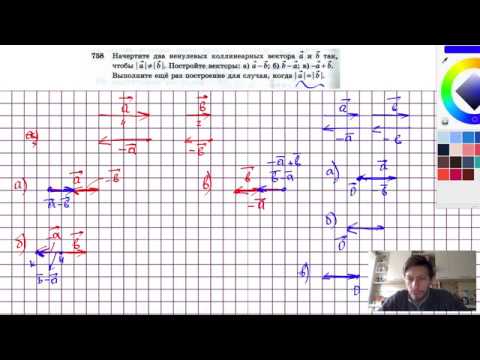
№758. Начертите два ненулевых коллинеарных вектора а и b так, чтобы | а |≠| b |. Постройте векторыСкачать