Даны множества трапеции прямоугольники четырехугольники (4 видео)

Лекция 2. Отношение между множествами.

Содержание

«Управление общеобразовательной организацией: новые тенденции и современные технологии»
(Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6?
В — МНОЖЕСТВО ТРЕУГОЛЬНИКОВ С — МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ Д — МНОЖЕСТВО ПРЯМОУГОЛЬНИКОВ Е — МНОЖЕСТВО КВАДРАТОВ А — МНОЖЕСТВО МНОГОУГОЛЬНИКОВ?
ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ?
Как может называться множество квадрат ромб круг?
Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты?
Решите систему неравенств?
Какой четырехугольник не имеет оси симметрии?
Какие из данных четырехугольников не являются параллелограммами 1 квадрат 2 прямоугольник 3 ромб 4 трапеция?
Построй диаграмму Венна для множества А, В, С, Д, где А — множество всех четырехугольников, В — множество ромбов, С — множество квадратов, д — множество прямоугольников?
Запиши множество острых , множество прямых и множество тупых углов на рисунке ?
Запиши множества острых, множество прямых и множество тупых углов на рисунке?
Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
📸 Видео

Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Лекция 2. Отношения между множествами.

Между двумя множествами существует пять видов отношений.

Если множества А и В не имеют общих элементов, то говорят, что эти множества не пересекаются и записывают этот факт в виде А∩В = ∅ . Например, А = < a , c , k >, В = < d , e , m , n >, общих элементов у этих множеств нет, поэтому множества не пересекаются.

Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются и записывают А∩В≠ ∅ . Например, множества А = < a , c , k > и В = < c , k , m , n > пересекаются, т. к. у них есть общие элементы c , k .

Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. (пишут В ⊂ А)

Пустое множество и само множество называют несобственными подмножествами . Остальные подмножества множества А называются собственными. Для каждого множества, состоящего из n элементов можно образовать 2 n подмножеств. Если рассматривают лишь подмножества некоторого множества U, то U называют универсальным множеством.

Если множества А и В состоят из одних и тех же элементов, то они называются равными.

Например, А = < a , c , k , m , n > и В = < m , n , a , c , k >, А = В.

Существует пять случаев отношений между двумя множествами. Их можно наглядно представить при помощи особых чертежей, которые называются кругами или диаграммами Эйлера-Венна.

Разбиение множества на классы называют классификацией.

Классификацию можно выполнять при помощи свойств элементов множества. Если выбирается только одно свойство, то такую классификацию называют дихотомической . Например, натуральные числа можно разбить на четные и нечетные. Буквы русского языка можно разбить на гласные и не гласные. Вообще, если на множестве Х задано одно свойство А, то это множество разбивается на два класса: первый класс – объекты, обладающие свойством А, второй класс – объекты, не обладающие свойством А.

Если элементы множества обладают двумя независимыми свойствами, то все множество разбивается на 4 класса. Например, на множестве натуральных чисел заданы два свойства: «быть кратным 2» и «быть кратным 3». При помощи этих свойств в множестве N можно выделить два подмножества А и В. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 6). Тогда в первый класс войдут числа, кратные 2 и 3, во второй – кратные 2, но не кратные 3, в третий – кратные 3, но не кратные 2, в четвертый – не кратные 2 и не кратные 3.

П р и м е р 1. Пусть Х – множество четырехугольников, А, В и С – его подмножества. Можно ли говорить о разбиении множества Х на классы А, В и С, если:

а) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, противоположные стороны которых не параллельны;

б) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, имеющих прямой угол?

Р е ш е н и е. а) Множества А, В и С попарно не пересекаются. Действительно, если у четырехугольника, противоположные стороны не параллельны, то он не может быть параллелограммом или трапецией. В параллелограмме противоположные стороны попарно параллельны, поэтому он не может принадлежать ни множеству В, ни множеству С. Наконец, в трапеции две противоположные стороны параллельны, а две другие не параллельны, поэтому трапеция не может принадлежать ни множеству А, ни множеству С. Объединение множеств А, В и С даст все множество четырехугольников. Условия классификации выполнены, множество всех четырехугольников можно разбить на параллелограммы, трапеции и четырехугольники, противоположные стороны которых не параллельны.

б) Множества А и В не пересекаются, но множества А и С имеют общие элементы, примером может служить прямоугольник, множества В и С тоже пересекаются: общим элементом является прямоугольная трапеция. Следовательно, нарушено первое условие классификации. Не выполняется и второе условие, так как некоторые четырехугольники не попадают ни в одно из подмножеств А, В или С, таким является четырехугольник с непараллельными сторонами и непрямыми углами. В этом случае множество Х на классы А, В и С не разбивается.

Задания для самостоятельной работы по теме:

Приведите примеры множеств А, В, С, если отношения между ними таковы:

2. Образуйте все подмножества множества букв в слове «крот». Сколько подмножеств получилось?

3 . Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 5. Постройте круги Эйлера для множеств N , A , B ; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N ; укажите характеристические свойства этих множеств.

5. Имеется множество блоков, различающихся по цвету (красные, желтые, зеленые), форме (круглые, треугольные, прямоугольные), размеру (большие, маленькие). На сколько классов разбивается множество, если в нем выделены подмножества: А – круглые блоки, В – зеленые блоки, С – маленькие блоки? Сделайте диаграмму Эйлера и охарактеризуйте каждый класс.

6. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) А ∩В=Ø

7. Пусть Х= < x N/ 1 x 15>. Задайте с помощью перечисления следующие его подмножества:

А – подмножество всех четных чисел;

В – подмножество всех нечетных чисел;

С – подмножество всех чисел, кратных 3;

D – подмножество всех чисел, являющихся квадратами;

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

(Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6?

Математика | 10 — 11 классы

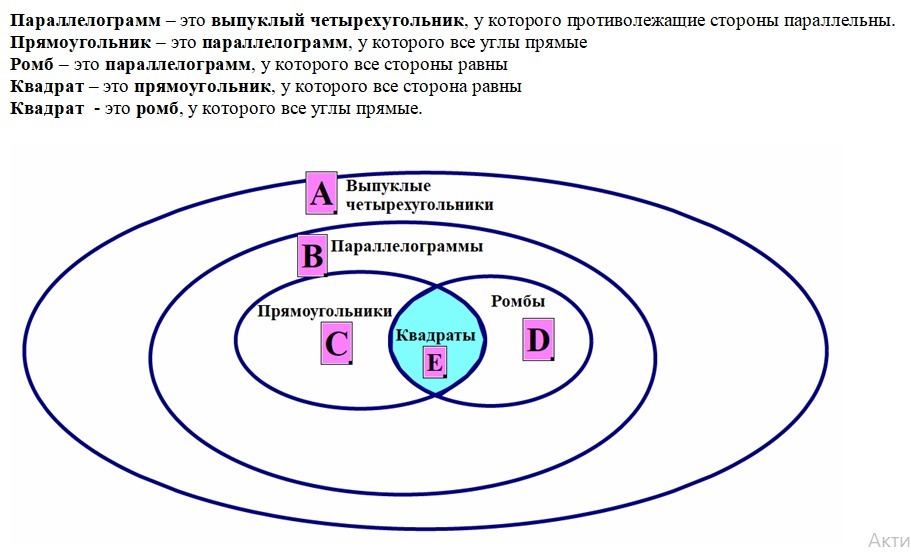
(Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6.

Покажите каждое из множеств.

Параллелограмм – это выпуклый четырехугольник, у которого противолежащие стороны параллельны.

Прямоугольник – это параллелограмм, у которого все углы прямые

Ромб – это параллелограмм, у которого все стороны равны

Квадрат – это прямоугольник, у которого все сторона равны

Квадрат — это ромб, у которого все углы прямые.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

В — МНОЖЕСТВО ТРЕУГОЛЬНИКОВ С — МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ Д — МНОЖЕСТВО ПРЯМОУГОЛЬНИКОВ Е — МНОЖЕСТВО КВАДРАТОВ А — МНОЖЕСТВО МНОГОУГОЛЬНИКОВ?

В — МНОЖЕСТВО ТРЕУГОЛЬНИКОВ С — МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ Д — МНОЖЕСТВО ПРЯМОУГОЛЬНИКОВ Е — МНОЖЕСТВО КВАДРАТОВ А — МНОЖЕСТВО МНОГОУГОЛЬНИКОВ.

Какие из этих множеств являются подмножествами других множеств?

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ?

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ!

Даны множества А, В, С.

Изобразите отношения между ними.

Укажите характеристическое свойство множеств АUВ, А∩С, А В, А ∩ (В С) : № 11.

А – множество учащихся в школе ;

В – множество девочек в школе ;

С – множество учащихся третьих классов в этой школе.

А – множество натуральных чисел ;

В – множество натуральных чисел, кратных 5 ;

С – множество натуральных чисел, кратных 4.

А – множество параллелограммов ;

В – множество четырехугольников ;

С – множество прямоугольников.

А – множество прямоугольников ;

В – множество четырехугольников ;

С – множество квадратов.

А – множество треугольников ;

В – множество прямоугольных треугольников ;

С – множество равнобедренных треугольников.

А – множество трапеций ;

В – множество параллелограммов ;

С – множество четырехугольников, имеющих прямой угол.

А – множество прямоугольных треугольников ;

В – множество равносторонних треугольников ;

С – множество равнобедренных треугольников.

А – множество натуральных чисел, кратных 5 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 4.

А – множество натуральных чисел, кратных 2 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 5.

А – множество параллелограммов ;

В – множество квадратов ;

С – множество ромбов.

Видео:Задача, которую боятсяСкачать

Как может называться множество квадрат ромб круг?

Видео:Четырехугольники. Вебинар | МатематикаСкачать

Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты?

Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты!

Видео:Геометрия 8 класс за 1 час | Математика | УмскулСкачать

Решите систему неравенств?

Решите систему неравенств.

На каком из рисунков изображено множество ее решений?

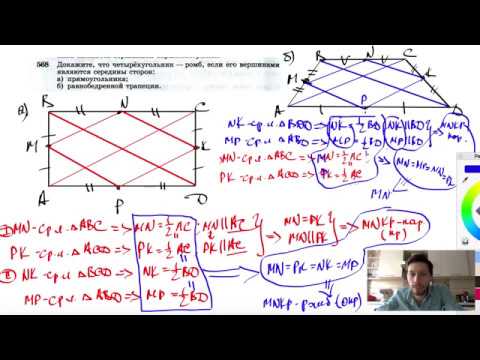
Видео:№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать

Какой четырехугольник не имеет оси симметрии?

A) ромб б) прямоугольник в) параллелограмм г) квадрат.

Видео:Свойства диагоналей прямоугольника. Геометрия 8 класс. Тесты. Четырехугольники. Математика.Скачать

Какие из данных четырехугольников не являются параллелограммами 1 квадрат 2 прямоугольник 3 ромб 4 трапеция?

Какие из данных четырехугольников не являются параллелограммами 1 квадрат 2 прямоугольник 3 ромб 4 трапеция.

Видео:Множества и операции над нимиСкачать

Построй диаграмму Венна для множества А, В, С, Д, где А — множество всех четырехугольников, В — множество ромбов, С — множество квадратов, д — множество прямоугольников?

Построй диаграмму Венна для множества А, В, С, Д, где А — множество всех четырехугольников, В — множество ромбов, С — множество квадратов, д — множество прямоугольников.

Видео:Параллелограмм. 8 класс.Скачать

Запиши множество острых , множество прямых и множество тупых углов на рисунке ?

Запиши множество острых , множество прямых и множество тупых углов на рисунке .

Есть ли среди данных фигур прямоугольники .

Из букв входящих в каждой множество составь слова.

Видео:8 класс, 6 урок, ТрапецияСкачать

Запиши множества острых, множество прямых и множество тупых углов на рисунке?

Запиши множества острых, множество прямых и множество тупых углов на рисунке.

Есть ли среди данных фигур прямоугольники?

На этой странице находится ответ на вопрос (Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6?, из категории Математика, соответствующий программе для 10 — 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Видео:9 класс, 2 урок, Множества и операции над нимиСкачать

Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы

Название	Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
Анкор	Praktikum_po_mat.doc
Дата	02.05.2017
Размер	7.87 Mb.
Формат файла
Имя файла	Praktikum_po_mat.doc
Тип	Контрольные вопросы #6276
страница	5 из 19

Подборка по базе: Answer 1 Вопросы к зачету АЭВМиВС_2021.docx, контрольные вопросы.docx, Контрольные вопросы.docx, А.1_новые вопросы.docx, ответы на вопросы .doc, Ответы на вопросы по астрономии.doc, Контрольные Вопросы.pdf, 2021 Контрольные работы для заочки маркетинг(Маркетинг).docx, Экзаменационные вопросы, задания-1631558497119.docx, Примерные вопросы для тестирования по теме лекций 2 и 3_.doc

Можно говорить о разбиении данного множества на попарно непересекающиеся подмножества или классы тогда, когда одновременно выполняются следующие условия:

Все подмножества, образующие разбиение, не пусты.
Любые два таких подмножества не пересекаются.

Объединение всех подмножеств есть данное множество. Условие 1 иногда опускают.

Символическая запись этого определения следующая.

Совокупность подмножеств А₁, А₂, . А_пназывается разбиением множества А на классы, а сами подмножества – классами, если выполняются условия:

А_i , i = 1, 2,…, n.
A_iA_j = , i, j = 1, 2, …,n; i  j.
A₁A₂…A_n = A

Рассмотрим задачи, связанные с оценкой правильности разбиения множества на классы и с самостоятельным разбиением множества на классы при использовании двух свойств.

Учащийся из множества четырехугольников выделил подмножества трапеций, параллелограммов и прямоугольников. Произошло ли разбиение множества на классы?

Пусть А – множество четырехугольников. А₁ – множество трапеций А₂ – множество параллелограммов, А₃ – множество прямоугольников.

Разбиение множества А на классы произойдет, если будут выполнены условия (1, 2, 3).

1. А_i, где i = 1, 2, 3, т.к. каждое множество содержит хотя бы по oдной фигуре.

Второе условие не выполняется, значит разбиения множества на классы не произошло.

На какие классы разбивается множество натуральных чисел, если использовать такие свойства: «делится на 2» и «быть однозначным»?

Обозначим через А множество четных натуральных чисел, В – множество однозначных чисел, N–множество натуральных чисел. Заметим, то А  В , т.к. некоторые четные числа являются однозначными, а некоторые однозначные числа – четными. Далее с помощью кругов Эйлера изобразим множества А, В, Nи выделим классы разбиения. Из рисунка видим, что их 4. Охарактеризуем каждый из них.

I – множество четных однозначных натуральных чисел.

II – множество четных неоднозначных натуральных чисел.

III – множество нечетных однозначных натуральных чисел.

IV – множество нечетных неоднозначных натуральных чисел.
Упражнения

93. Из множества Р = выделили подмножества А, В и С. Выясните, в каком случае произошло разбиение множества Р на классы:

94. Множество А состоит из 3, 4, 5, 6, 7, 8, 9; множество В – его подмножество, состоящее из чисел, которые делятся на 3; множество С – подмножество, состоящее из чисел, которые при делении на 3 дают в остатке 1; множество D – подмножество, состоящее из чисел, которые при делении на 3 дают в остатке 2. Можно ли утверждать, что множество А разбивается в этом случае на попарно непересекающиеся подмножества В, С и D? Произошло ли разбиение множества на классы, если да, то сколько классов?

95. На координатной прямой выделены два множества: (–;2) и (2; +). Можно ли утверждать, что множество действительных чисел разбито на два класса? Можно ли разбить множество точек координатной прямой на 3 класса? на 4 класса? Ответ проиллюстрируйте на примере.

96. Выясните, в каких случаях классификация выполнена верно:

а) треугольники делятся на прямоугольные, тупоугольные и равнобедренные;

б) углы классифицируются на острые, прямые и развернутые;

в) целые числа можно разбить на натуральные числа, число 0 и отрицательные целые числа;

г) глаголы русского языка делятся на глаголы настоящего, прошедшего и будущего времени;

д) члены предложения бывают главные и второстепенные.

97. Из множества Т треугольников выделили два подмножества: X– подмножество прямоугольных треугольников и Y – подмножество равнобедренных треугольников. Постройте для данных множеств круги Эйлера; установите, на сколько непересекающихся областей разбился круг, изображающий множество Т, и все множества, изображенные этими областями, задайте описанием характеристического свойства. При помощи скольких свойств произведено разбиение множества треугольников на классы?

98. Разбейте множество четырехугольников на классы: а) по какому-либо одному свойству; б) по двум свойствам. Укажите эти свойства, для каждого случая постройте круги Эйлера, установите число непересекающихся областей и выясните, какие множества изображаются этими областями.

99. Множества Р ромбов, Т треугольников и К многоугольников, имеющих угол 30°, являются подмножествами множества М многоугольников. Постройте круги Эйлера для данных множеств, установите, на сколько непересекающихся областей разбился круг, изображающий множество М, и для всех множеств, изображенных этими областями, укажите характеристическое свойство.

100. Из множества треугольников выделены подмножества прямоугольных, равнобедренных и тупоугольных треугольников. Произошло ли разбиение множества на классы?

101. Произведите разбиение на классы множества целых чисел, используя свойства «быть кратным 4» и «быть кратным 5».

102. Укажите классы разбиения множества треугольников, которые получаются при рассмотрении таких свойств, как «иметь хотя две равные стороны» и «иметь прямой угол».

103. Из множества четырехугольников выделили следующие подмножества: а) прямоугольников, не являющихся ромбами; б) ромбов не являющихся прямоугольниками; в) квадратов; г) четырехугольников, не являющихся ни ромбами, ни прямоугольника. Произошло ли разбиение множества на классы?

104. Истинно ли высказывание: «Параллелограммы делятся на прямоугольники, ромбы и квадраты»? Почему?

105. На множестве геометрических фигур плоскости выделены множества фигур, имеющих: а) центр симметрии; б) ось симметрии; в) не имеющих ни центра, ни оси симметрии. Можно ли считать, что произошло разбиение множества на классы?

106. Произведите разбиение множества целых чисел на классы используя такие свойства: «быть однозначным числом» и «быть двузначным числом».

107. Укажите, какие классы разбиения получаются при рассмотрении на множестве треугольников таких свойств: «иметь тупой угол» и «все углы острые».

108. Произошло ли разбиение множества натуральных чисел на классы, если из него выделены подмножества чисел, делящихся на три чисел, которые при делении на 3 дают остаток 1?

109. Установите, правильны ли следующие классификации:

а) натуральные числа делятся на однозначные, двузначные и трехзначные;

б) параллелограммы могут быть прямоугольниками, квадратами и ромбами;

в) треугольники бывают равносторонними и неравносторонними;

г) четырехугольники делятся на параллелограммы и трапеции.

110. Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 4. Постройте круги Эйлера для множеств N, А и В; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N; укажите характеристические свойства этих множеств.

111. Из множества параллелограммов выделили подмножество прямоугольников и подмножество квадратов. Постройте круги Эйлера для данных множеств. Можно ли утверждать в данном случае, что множество параллелограммов разбито на 3 попарно непересекающихся подмножества: квадраты; прямоугольники, не являющиеся квадратами; параллелограммы, не являющиеся прямоугольниками?
6. ДЕКАРТОВО УМНОЖЕНИЕ МНОЖЕСТВ

Определение 9. Декартовым произведением множеств А и В называют множество АВ, элементами которого являются все пары(х,у), такие, что х  А, уВ, т.е. АВ = .

Найдем, например, декартово произведение множеств А = <1,3> и В =.

Операцию, при помощи которой находят декартово произведение, называют декартовым умножением множеств.

Декартово умножение множеств не обладает ни свойством коммутативности, ни свойством ассоциативности, но связано с операциями объединения и вычитания множеств дистрибутивными свойствами:

для любых множеств А, В, С имеют место равенства:

Для наглядного представления декартова произведения числовых множеств часто используют прямоугольную систему координат.

Пусть А и В – числовые множества. Тогда элементами декартова произведения этих множеств будут упорядоченные пары чисел. Изобразив каждую пару чисел точкой на координатной плоскости, получим фигуру, которая и будет наглядно представлять декартово произведение множеств А и В.

Изобразим на координатной плоскости декартово произведение множеств А и В, если:

В случае а) данные множества конечны и можно перечислить элементы декартова произведения.

АВ = . Построим оси координат и на оси ОХ отметим элементы множества А, а на оси ОУ – элементы множества В. Затем изобразим каждую пару чисел множества АВ точкам на координатной плоскости (рис.7). Полученная фигура из четыре точек и будет наглядно представлять декартово произведение данных множеств А и В.

В случае б) перечислить все элементы декартова произведения множеств невозможно, т.к. множество В – бесконечное, но можно представить процесс образования этого декартова произведения: в каждой паре первая компонента либо 2, либо 6, а вторая компонента – действительное число из промежутка [1,4].

Все пары, первая компонента которых есть число 2, а вторая пробегает значение от 1 до 4 включительно, изображаются точками отрезка СД, а пары, первая компонента которых есть число 6, а вторая – любое действительное число из промежутка [1,4], – точками отрезка РS(рис.8). Таким образом, в случае б) декартово произведение множеств А и В на координатной плоскости изображается в виде отрезка СД и РS.

Рис. 7 Рис. 8 Рис. 9
Случай в) отличается от случая б) тем, что здесь бесконечно не только множество В, но и множество А, поэтому,первой компонентой пар, принадлежащих множеству АВ, является любое число из промежутка [2, 6]. Точки, изображающие элементы декартова произведения множеств А и В, образуют квадрат СДЕL(рис. 9). Чтобы подчеркнуть, что элементы декартова произведения изображаются точками квадрата, его можно заштриховать.
Контрольные вопросы

Покажите, что решение следующих задач приводит к образованию декартова произведения множеств:

а) Запишите все дроби, числителем которых является число из множества А =, а знаменателем – число из множества В = <5,6, 7>.

б) Запишите различные двузначные числа, используя числа 1, 2, 3, 4.

Докажите, что для любых множеств А, В, С справедливо равенство (АВ)С = (АС)(ВС). Проиллюстрируйте его выполнимость для множеств А= ,В=, С = .
Какую фигуру образуют точки на координатной плоскости, если их координаты являются элементами декартова произведения множеств А = и В = R
Определите, декартово произведение каких множеств А и В изображено на рисунке 10.

112. Запишите все двузначные числа, цифры десятков которых принадлежат множеству А = , а цифры единиц – множеству В = .

113. Напишите все дроби, числители которых выбираются из множества А= <3, 5, 7>, а знаменатель – из множества В= .

114. Напишите все правильные дроби, числители которых выбираются из множества А = , а знаменатель – из множества В= <4, 6,8>.

116.Известно, что АВ = . Установите, из каких элементов состоят множества А и В.

119. Известно, что АВ = . Установите, из каких элементов состоят множества А и В.

120. Найдите декартово произведение множеств А = и В = и выделите из него подмножество пар, в которых:

а) первая компонента больше второй; б) первая компонента равна 5; в) вторая компонента равна 7.

121. Перечислите элементы, принадлежащие декартову произведению множеств А, В и С, если:

122. Изобразите на координатной плоскости элементы декартова про
изведения множеств А и В, если:

125. Фигуры, приведенные на рис. 14, являются результатом изображения на координатной плоскости декартова произведения множеств X и Y. Укажите для каждой фигуры эти множества.

126. Выясните, декартово произведение каких двух множеств изображается на координатной плоскости в виде полуплоскости. Рассмотрите все случаи.

127. Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде прямого угла, который образуется при пересечении координатных осей.

128. На координатной плоскости постройте прямую, параллельную оси ОХ и проходящую через точку Р (–2, 3). Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде этой прямой.

129. На координатной плоскости постройте прямую, параллельную оси ОY и проходящую через точку Р (–2, 3). Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде этой прямой.

130. На координатной плоскости постройте полосу, ограниченную прямыми, проходящими через точки (–2, 0) и (2, 0) и параллельными оси ОY. Опишите множество точек, принадлежащих этой полосе.

131. На координатной плоскости постройте прямоугольник, вершинами которого служат точки А (–3, 5), В (–3, 8), С (7, 5), D(7, 8). Опишите множество точек этого прямоугольника.

132. Постройте на координатной плоскости множество точек, координаты которых удовлетворяют условию:

133. На координатной плоскости изобразите элементы декартова произведения множеств XиY, если:

а) X = R, Y = ; б) X = R, Y = [–3; 3]; в) X = [0; ), Y = (, 0].

134. На координатной плоскости постройте фигуру F, если

135. Постройте прямоугольник с вершинами в точках (–3, 4), (–3, –3), (1, –3), (1, 4). Укажите характеристическое свойство точек, принадлежащих этому прямоугольнику.

136. На координатной плоскости постройте прямые, параллельные оси ОХ и проходящие через точки (2, 3) и (2, –1). Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде полосы, заключенной между построенными прямыми.

137. На координатной плоскости постройте прямые, параллельные оси ОY и проходящие через точки (2, 3) и (–2, 3). Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде полосы, заключенной между построенными прямыми.

138. Изобразите в прямоугольной системе координат множество XY, если:

📸 Видео

Множества. Операции над множествами. 10 класс алгебраСкачать

ЧЕТЫРЕХУГОЛЬНИКИ ПАРАЛЛЕЛОГРАММ ПРЯМОУГОЛЬНИК РОМБ КВАДРАТ ТРАПЕЦИЯ МНЕМОСТИХИ ЗАГАДКИСкачать

Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебраСкачать

Найдите площадь четырёхугольникаСкачать

Множество. Элементы множества. 5 класс.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Симедиана. Гармонические четырехугольники. | Олимпиадная математикаСкачать

Даны множества трапеции прямоугольники четырехугольники

«Управление общеобразовательной организацией: новые тенденции и современные технологии»