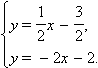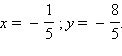Задачи с решениями

Установить, пересекаются, параллельны или совпадают данные пары прямых; в случае пересечения прямых найти координаты точки их пересечения:

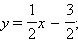
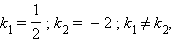
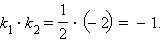
а) Найдем угловые коэффициенты прямых. Первое уравнение имеет вид второе уравнение Отсюда но Следовательно (см теорему 11.13) прямые перпендикулярны и пересекаются. Для нахождения точки пересечения (общей точки) прямых решим совместно два уравнения

Отсюда получим

б) Умножим первое уравнение на (-2) и получим Это уравнение совпадает с уравнением второй прямой, т. е. прямые совпадают.

в) Умножим первое уравнение на (-3) и получим Второе уравнение имеет вид Коэффициенты при одинаковых переменных равно, но свободные члены при этом различны. Следовательно (см теорему 11.14) прямые параллельны.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Точка пересечения прямых в пространстве онлайн

С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Точка пересечения прямых в пространстве − теория, примеры и решения

• Содержание
• 1. Точка пересечения прямых, заданных в каноническом виде.
• 2. Точка пересечения прямых, заданных в параметрическом виде.
• 3. Точка пересечения прямых, заданных в разных видах.
• 4. Примеры нахождения точки пересечения прямых в пространстве.

1. Точка пересечения прямых в пространстве, заданных в каноническом виде.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L₁ и L₂:

,

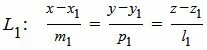(1)

,

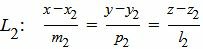(2)

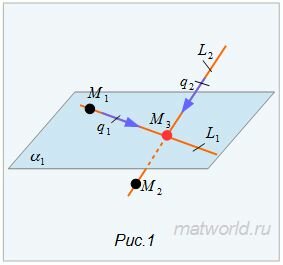
Найти точку пересечения прямых L₁ и L₂ (Рис.1).

Запишем уравнение (1) в виде системы двух линейных уравнений:

,

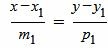(3)

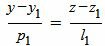(4)

Сделаем перекрестное умножение в уравнениях (3) и (4):

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

Аналогичным образом преобразуем уравнение (2):

Запишем уравнение (2) в виде системы двух линейных уравнений:

,

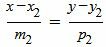(7)

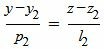(8)

Сделаем перекрестное умножение в уравнениях (7) и (8):

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:

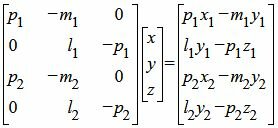(11)

Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L₁ и L₂ не пересекаются. Если система (11) имеет множество решений, то прямые L₁ и L₂ совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L₁ и L₂ .

2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L₁ и L₂ в параметрическом виде:

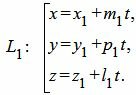(12)

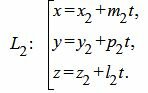(13)

Задачу нахождения нахождения точки пересечения прямых L₁ и L₂ можно решить разными методами.

Метод 1. Приведем уравнения прямых L₁ и L₂ к каноническому виду.

Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:

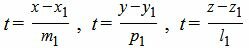(14)

Так как левые части уравнений (14) равны, то можем записать:

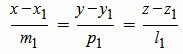(15)

Аналогичным образом приведем уравнение прямой L₂ к каноническому виду:

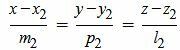(16)

Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.

Метод 2. Для нахождения точки пересечения прямых L₁ и L₂ решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:

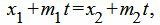(17)

(18)

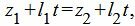(19)

Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).

3. Точка пересечения прямых в пространстве, заданных в разных видах.

Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.

4. Примеры нахождения точки пересечения прямых в пространстве.

Пример 1. Найти точку пересечения прямых L₁ и L₂:

(20)

(21)

Представим уравнение (20) в виде двух уравнений:

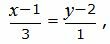(22)

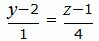(23)

Сделаем перекрестное умножение в уравнениях (22) и (23):

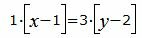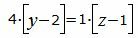Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

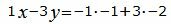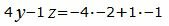Аналогичным образом поступим и с уравнением (2).

Представим уравнение (2) в виде двух уравнений:

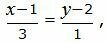(26)

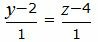(27)

Сделаем перекрестное умножение в уравнениях (7) и (8)

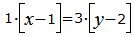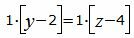Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

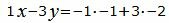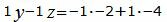Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:

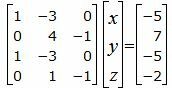(30)

Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

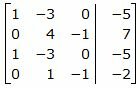Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строку 3 со строкой 1, умноженной на −1:

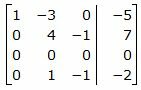Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:

Сделаем перестановку строк 3 и 4.

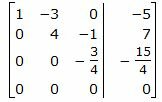Второй этап. Обратный ход Гаусса.

Исключим элементы 3-го столбца матрицы выше элемента a₃₃. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:

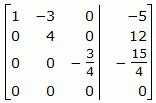Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:

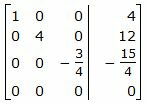Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

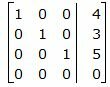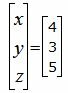Ответ. Точка пересечения прямых L₁ и L₂ имеет следующие координаты:

Пример 2. Найти точку пересечения прямых L₁ и L₂:

(31)

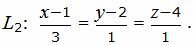(32)

Приведем параметрическое уравнение прямой L₁ к каноническому виду. Выразим параметр t через остальные переменные:

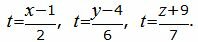Из равентсв выше получим каноническое уравнение прямой:

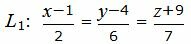(33)

Представим уравнение (33) в виде двух уравнений:

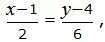(34)

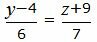(35)

Сделаем перекрестное умножение в уравнениях (34 и (35):

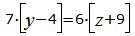Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

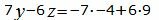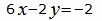(36)

.

(37)

Аналогичным образом поступим и с уравнением (2).

Представим уравнение (2) в виде двух уравнений:

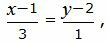(38)

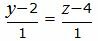(39)

Сделаем перекрестное умножение в уравнениях (38) и (39)

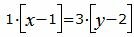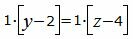Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

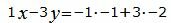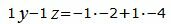Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:

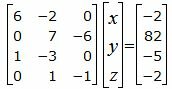(42)

Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:

Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:

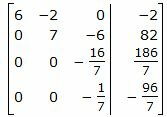Исключим элементы 3-го столбца матрицы ниже элементаa₃₃. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:

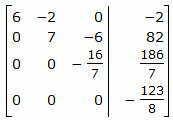Из расширенной матрицы восстановим последнюю систему линейных уравнений:

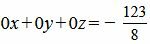(43)

Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L₁ и L₂ не пересекаются. То есть они или параллельны, или скрещиваются.

Прямая L₁ имеет направляющий вектор q₁=, а прямая L₂ имеет направляющий вектор q₂=. Эти векторы не коллинеарны. Следовательно прямые L₁ и L₂ скрещиваются .

Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

Точка пересечения двух прямых на плоскости

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Пересечение прямых

Для создания компьютерных игр, программ математических графиков, расчетов движения объектов и т.п. очень часто требуется найти точку пресечения прямых. Сначала необходимо на бумаге вывести и упростить формулы вычисления и далее эти формулы перевести в программный код.

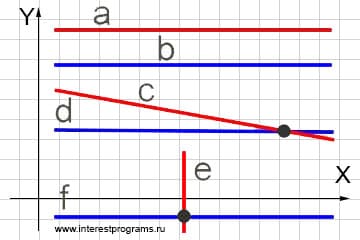
Прямые это бесконечные линии, поэтому на плоскости они всегда пересекаются. Если прямые не пересекаются значит они параллельны. Частные случаи поведения прямых на плоскости: прямые неопределенны, прямые параллельны, прямые совпадают, одна из прямых параллельна оси X или Y. Общие случаи «нормального» пересечения прямых и частные случаи учитываются в программном коде класса Intersections прикрепленного исходника.

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Прямые пересекаются

Даны две прямые AB и CD расположенные на одной плоскости. Они пересекаются и необходимо найти точку пересечения. За основу берем классическое уравнение прямой и подставляя данные получаем систему уравнений для двух прямых.

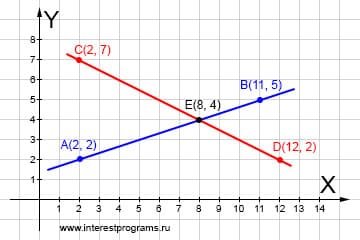
Точку пересечения можно найти, решая совместно уравнения прямых. Два уравнения — две неизвестных величины. Если количество уравнений больше или равно количеству неизвестных, то система решаема. Точка пересечения двух прямых это такая точка, которая принадлежит обеим прямым.

Классическое уравнение прямой: Запишем уравнение в одну строчку: Вычислим коэффициенты и свободные члены: В итоге получаем уравнение прямой с коэффициентами:

Уравнение с линейными коэффициентами отличается от уравнения с угловым коэффициентом отсутствием операции деления. Минимум операций деления упрощает создание устойчивого программного кода.

Видео:16. Показать что прямые пересекаются и найти точку их пересечения в пространствеСкачать

Точка пересечения прямых

Координаты точки пересечения это числа которые являются решением для каждого из уравнений прямых. Решая систему из двух уравнений находим в какой точке пересекаются прямые AB и CD.

Подставляем известные данные: Получаем два уравнения: Решаем систему уравнений: Найдено, прямые пересекаются в точке с координатами:

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Прямые параллельны

Если прямые параллельны и лежат друг от друга на расстоянии, то у них нет общих точек. Совместная система уравнений не имеет решений. Эти уравнения существуют как бы сами по себе. В точности как их параллельные прямые.

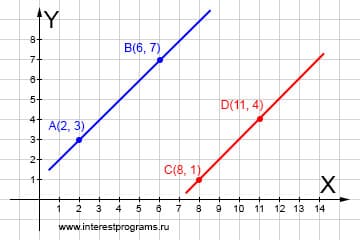
Две прямые могут полностью совпадать, в таком случае у них бесконечное количество общих точек. Совпадение прямых означает равность коэффициентов и свободных членов уравнений. Совпадающие прямые имеют идентичные уравнения.

Применяя формулу у.2 выведем уравнения прямых: Получаем систему уравнений:

Итог: система уравнений параллельных прямых не имеет решений.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Уравнение в программный код

На бумаге всё славненько, надо также сделать и в программном коде. Но программы не разбираются в уравнениях, им подавай переменные, постоянные и функции. Программный код не терпит неопределенности, он требует точные данные. Очень желательно строить выражения без операций деления. Преобразуем в программный код уравнение с коэффициентами (у.3) описанное выше. Для каждой прямой своё уравнение и переменные.

Точки определяющие прямые запишем в структуры Point. У каждой прямой две точки и они являются входными данными:
Определяем коэффициенты и свободные члены уравнений. Записываем их в соответствующие переменные:
Точка пересечения также будет храниться в структуре Point:

Видео:Стереометрия для ЕГЭ: 2 - параллельные и скрещивающиеся прямыеСкачать

Вывод результата

В выражениях присутствует деление. Но знаменатель только тогда и только тогда будет равен нулю, когда обе прямые будут параллельны или оси X или оси Y. В этом случае они не пересекаются или совпадают. Это отслеживаемые состояния в классе Intersections , и вывод информации заканчивается до выбрасывания исключения при делении на ноль.

Видео:7. Скрещивающиеся прямыеСкачать

Проверка параллельности и совпадения

Видео:10 класс - Геометрия - Скрещивающиеся прямыеСкачать

Проверка на перпендикулярность

Видео:Параллельность прямых. 10 класс.Скачать

Класс Intersections

Исходник представляет собой два класса: класс вычисления точки пересечения прямых и информационный класс выдающий множество дополнительных сведений о свойствах исследуемых прямых.

Краткий листинг исходника дающий представление о структуре классов:

Видео:15. Взаимное расположение прямых в пространствеСкачать

Применение класса Intersections

Класс class Intersections легко встраивается в любой исходный код. Точки определяющие прямые являются входными данными. На выходе получаем результат пересечения, координаты точки пересечения. Для дальнейшей обработки результатов можно использовать идентификатор свойства пересечения и дополнительную текстовую информацию.

Видео:Параллельность прямых. Практическая часть. 10 класс.Скачать

Прикрепленный файл

Прикрепленный файл архива содержит исходник классов Intersections, Info и программу демонстрирующую работу класса Intersections в режиме вычисления точки пересечения прямых на плоскости. Исходный код написан на языке C#, но его легко можно преобразовать в код на другом языке программирования. Для работы демонстрационной программы необходима установка платформы. .NET Core 3.1.

Скачать исходник

• Файл: IntersectionsLineLine.zip
• Размер: 84 Кбайт
• Загрузки: 505

Похожая тематика

Пересечение луча и прямой на плоскости »

📹 Видео

Взаимное расположение прямых в пространстве. Видеоурок 3. Геометрия 10 классСкачать

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Взаимное расположение прямых на плоскости. 7 класс.Скачать

Угол между прямыми в пространстве. 10 класс.Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать