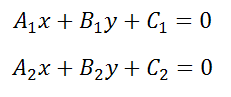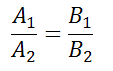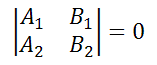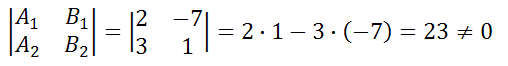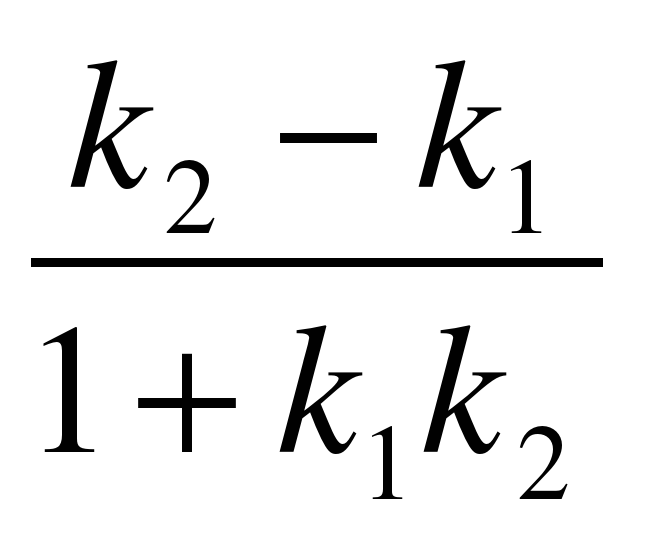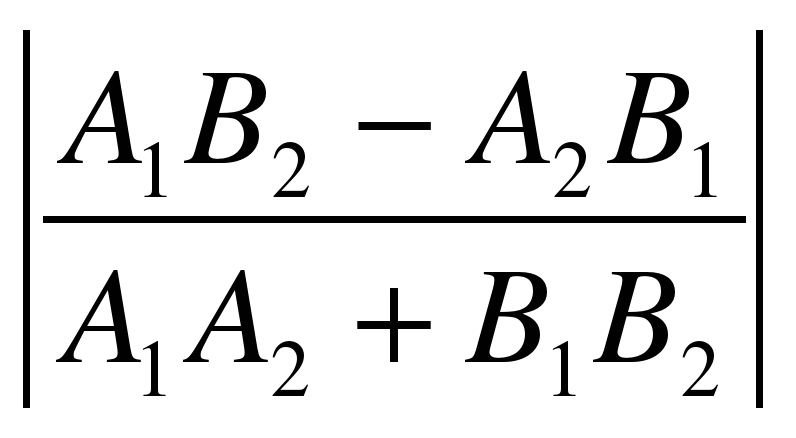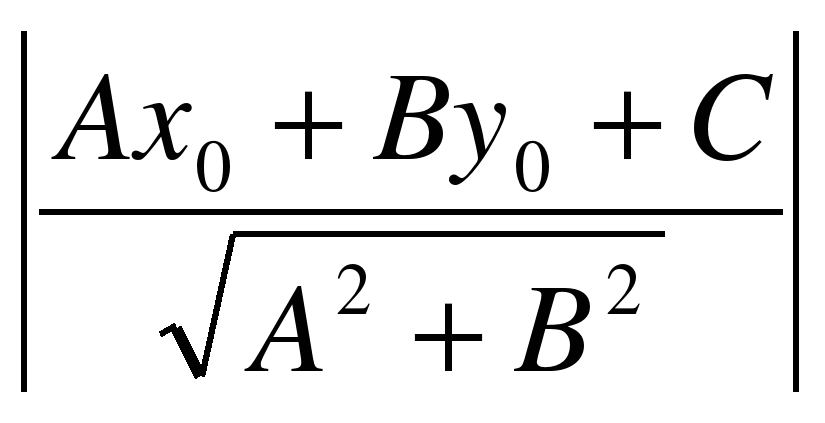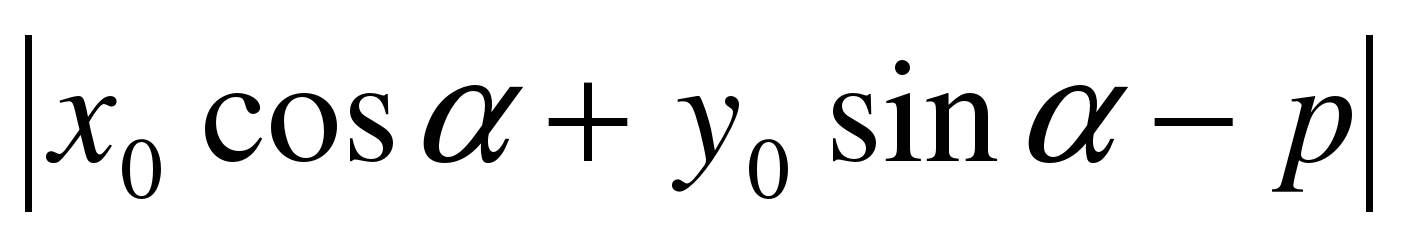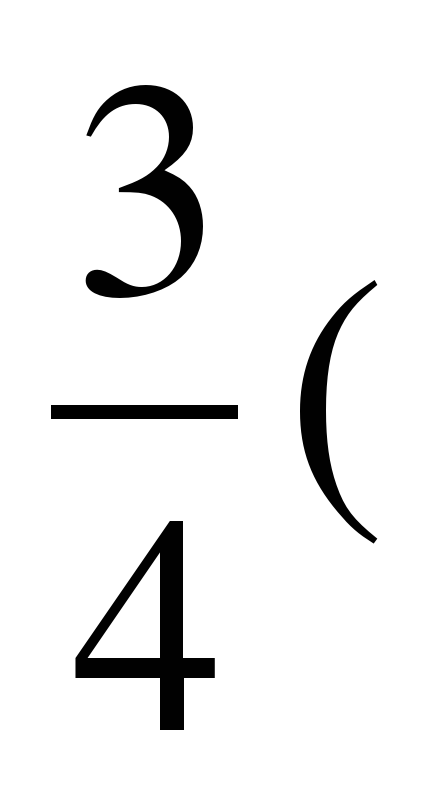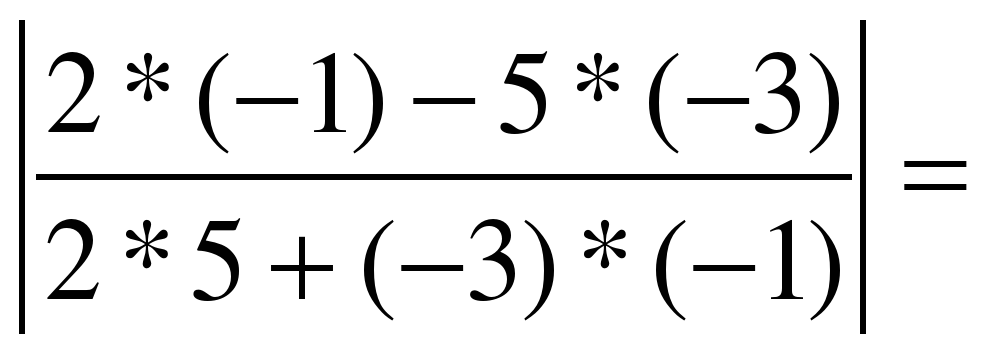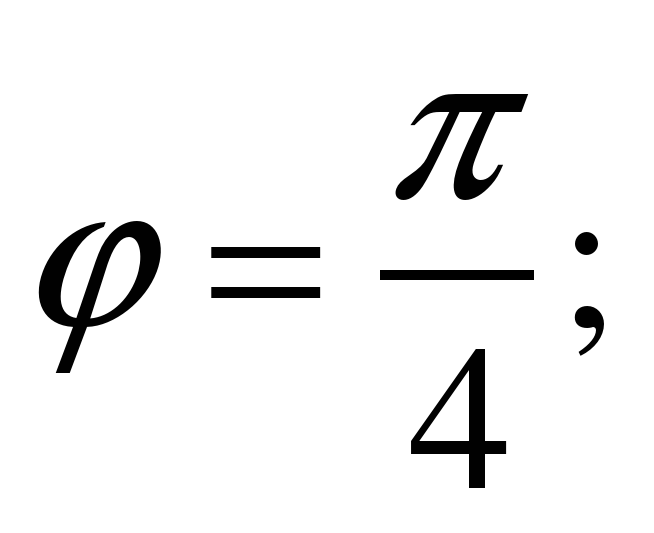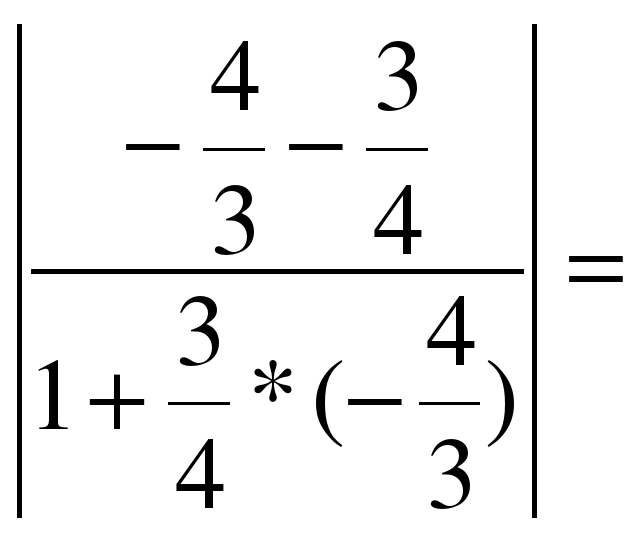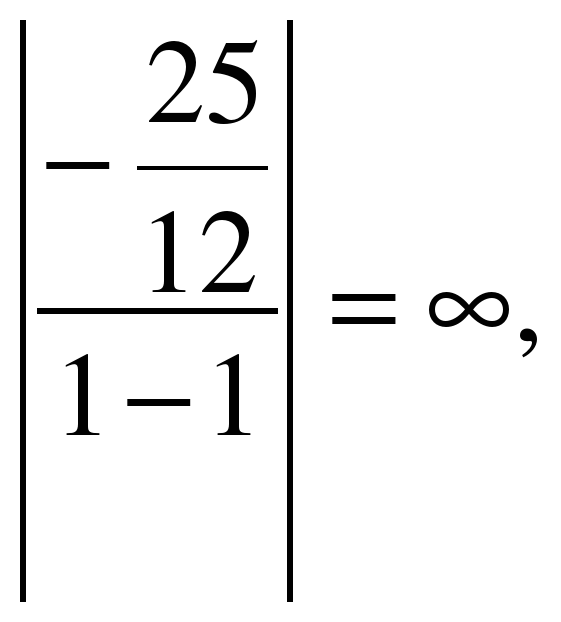Дана прямая y 2x 4 какая из следующих параллельна данной (2 видео)

Условие параллельности прямых

Необходимым и достаточным условием параллельности двух прямых, заданных уравнением:

служит равенство их угловых коэффициентов, то есть

Если прямые заданы уравнениями в общем виде, то есть

то условие параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны:

или в другом представлении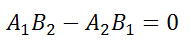

Также это равенство можно записать в виде

Если свободные члены пропорциональны, то есть,

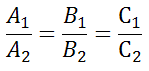
то прямые не только параллельны, но и совпадают.

4x+2y-8=0 и 8x+4y-16=0

представляют одну и ту же прямую, то есть совпадают.

Пример 2
Прямые у=4x-3 ( на графике синего цвета ) и y=4x+7 ( прямая красного цвета ) параллельны, так как у них угловые коэффициенты равны k₁=k₂=4

Пример 3
Прямые у=5x+1 и y=3x-4 не параллельны, так как у них угловые коэффициенты не равны, т.е. k₁=5, k₂=3

Пример 4
Прямые 2x+4y+7=0 и 3x+6y-5=0 параллельны, так как выражение равно нулю

Пример 5
Прямые 2x-7y+7=0 и 3x+y-5=0 не параллельны, так как выражение не равно нулю

Содержание

1) Какая из точек принадлежит графику функции, заданной формулой y=-3x? 1)A(2;6) 2)B(-2;6) 3)C(-2;-6) 4)D(2;-1) 2) Укажите формулу,задающую линейную функцию, график которой параллелен оси ox 1)y=2x+6 2)y=-4x 3)y=9 4)x=-5 3) Найдите абсциссу точки пересечения прямой 5x+3y-15=0 с осью ox ПОМОГИТЕ ПОЖАЛУЙСТА ДАЮ 30 БАЛЛОВ. НАЙДИТЕ КООРДИНАТЫ ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯМОЙ 6x-7y+12=0 с осью ox. В ответ укажите абсциссу этой точки
Взаимное расположение прямых
Просмотр содержимого документа «Взаимное расположение прямых»
💥 Видео

Видео:Задание 7 ЕГЭ по математикеСкачать

1) Какая из точек принадлежит графику функции, заданной формулой y=-3x? 1)A(2;6) 2)B(-2;6) 3)C(-2;-6) 4)D(2;-1) 2) Укажите формулу,задающую линейную функцию, график которой параллелен оси ox 1)y=2x+6 2)y=-4x 3)y=9 4)x=-5 3) Найдите абсциссу точки пересечения прямой 5x+3y-15=0 с осью ox ПОМОГИТЕ ПОЖАЛУЙСТА ДАЮ 30 БАЛЛОВ. НАЙДИТЕ КООРДИНАТЫ ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯМОЙ 6x-7y+12=0 с осью ox. В ответ укажите абсциссу этой точки

1) В принадлежит, если подставишь в y=-3xвместо х абсциссу точки В, а вместо у ординату точки В.

2) ответ номер 3, у=9, так как он параллелен оси х
3)5х+3·0 -15=0
5х-15=0
5х=15
х=3 точка А(3;0) -точка пересечения графика с осью ох.
4) 6x-7y+12=0 вместо у подставляем нуль и считаем, 6х-7 ·0 +12=0
6х=-12
х=-2 это и есть абсцисса
В(-2;0) -точка пересечения графика с осью ох.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Взаимное расположение прямых

Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых, пересечение прямых, расстояние от данной точки до данной прямой.

Просмотр содержимого документа
«Взаимное расположение прямых»

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ.

Под углом между прямыми в плоскости понимают меньший (острый) из двух смежных углов образованными этими прямыми.

Если прямые l₁ и l₂ заданы уравнениями с угловыми коэффициентами у=к₁х+b₁ и у=к₂х+b_2, то угол φ между ними вычисляется по формуле

tg φ=

Условие параллельности прямых l₁ и l₂ имеет вид

а условие их перпендикулярности

k₁ = — 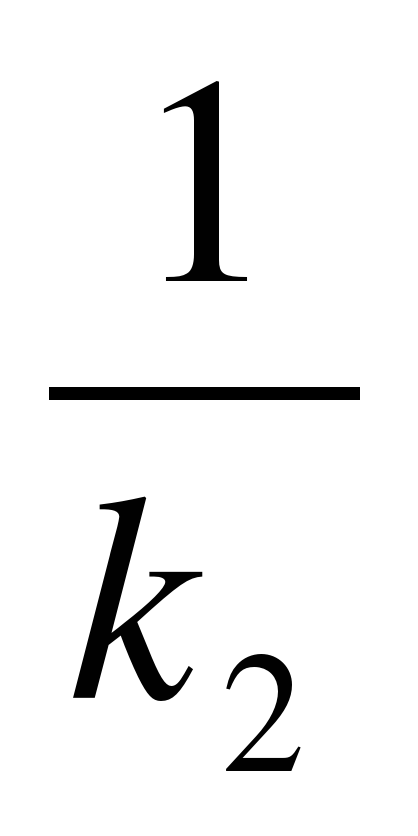(или k₁k₂= — 1)

то величина φ угла между ними вычисляется по формуле

tg φ=

угловые их параллельности

( или А₁В₂-А₂В₁=0)

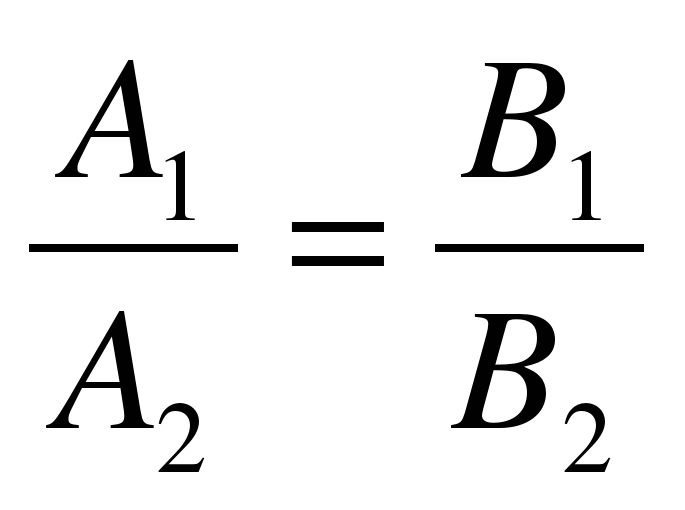
Условие их перпендикулярности

Для нахождения общих точек прямых l₁ и l₂ необходимо решить систему

уравнений

А₁х+В₁у+С₁=0, у=k₁x+b₁

или

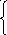
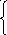
Если 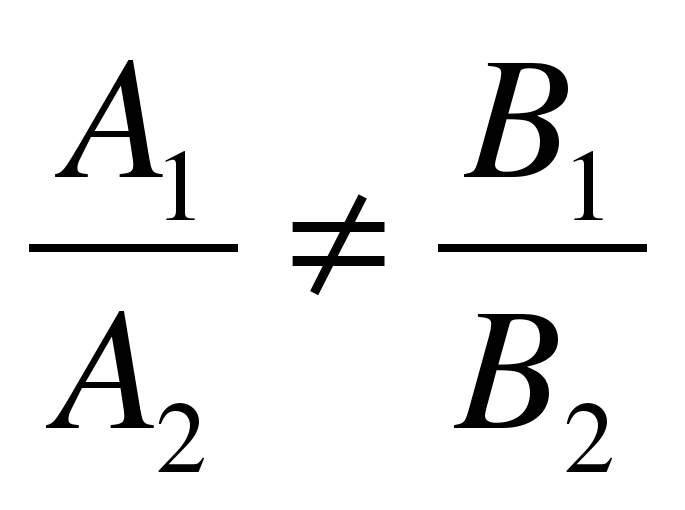, то имеется единственная точка пересечения прямых ;

Если 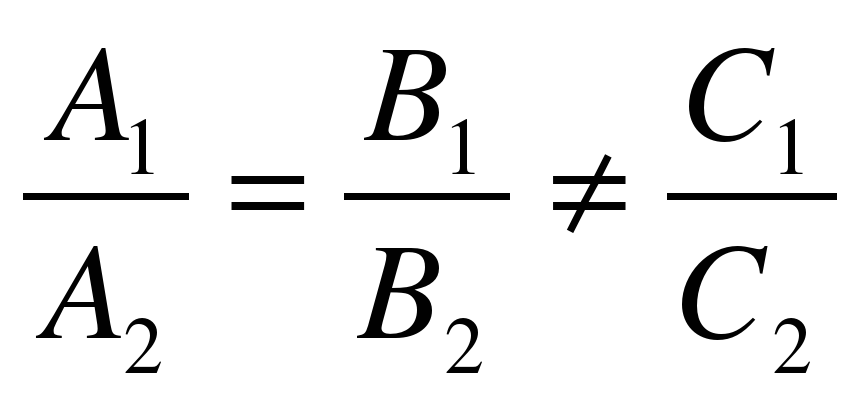— прямые l₁ и l₂ не имеет общей точки, т. е параллельны;

Если 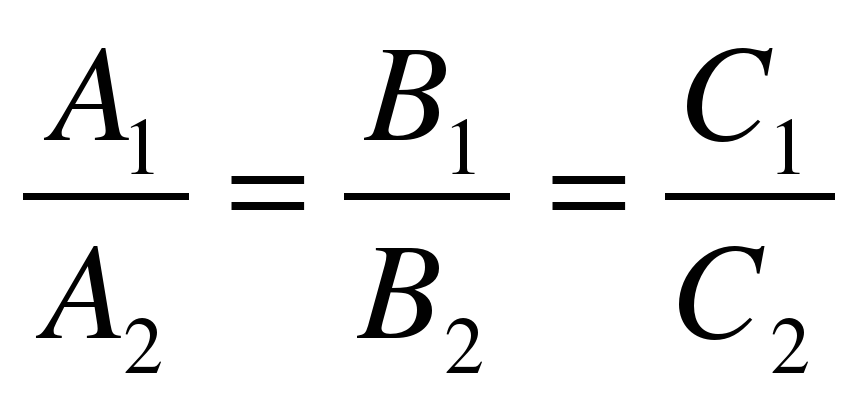-прямые имеют бесконечное множество точек т.е совпадают

Расстоянием d от точки М₀ (х₀;у₀) до прямой Ах+Ву+С=0 называется длина перпендикуляра , опущенного из этой точки на прямую .

Расстояние d определяется по формуле

Расстояние от точки М₀ (х₀;у₀) до прямой х cos + y sin— p=0 вычисляется по формуле

ПРИМЕР: найти угол между прямыми :

1) y=2x-3 и y=;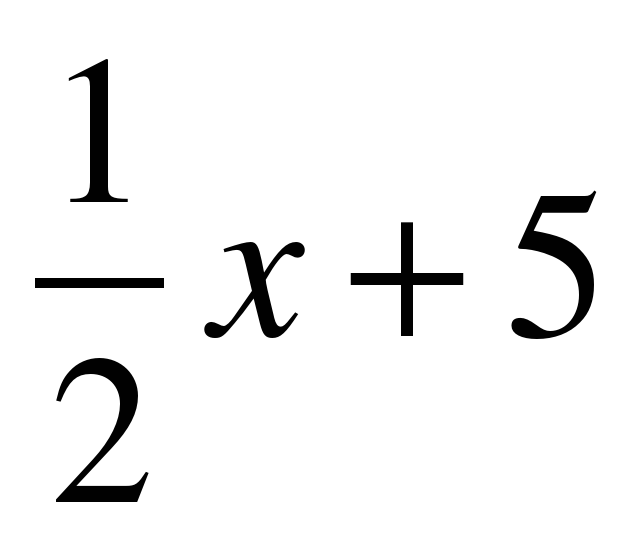

2) 2x-3y+10=0 и 5x – y+4=0;

3) y= 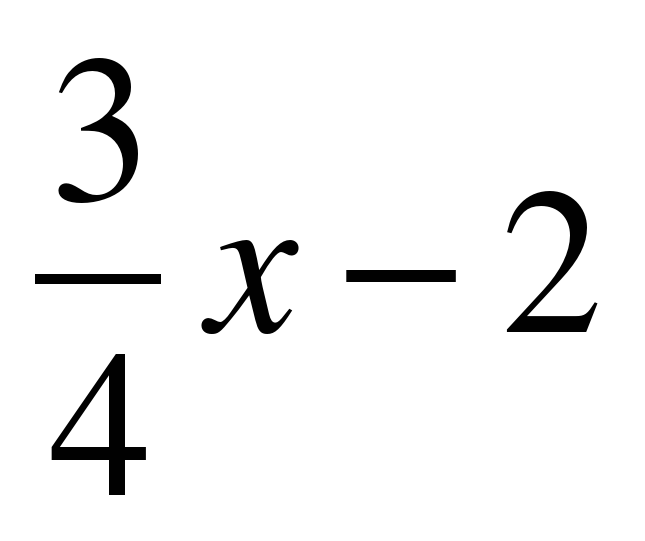и 8x+6y+5=0;

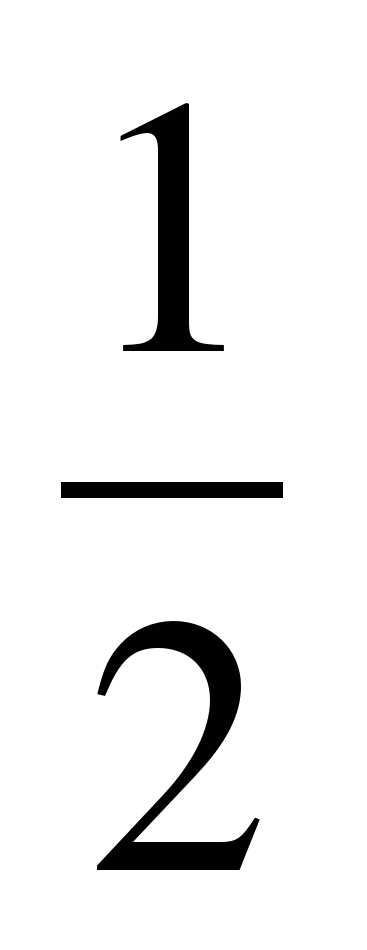
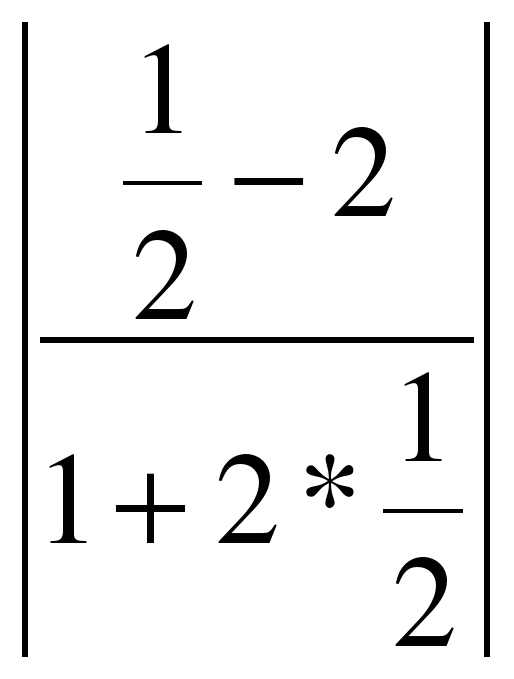
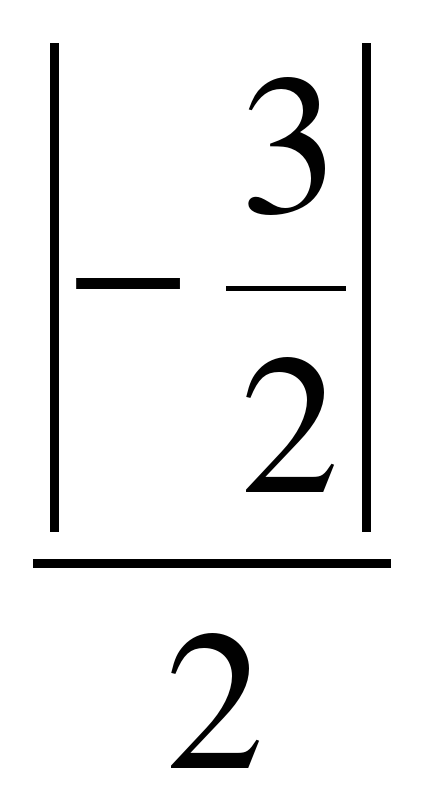
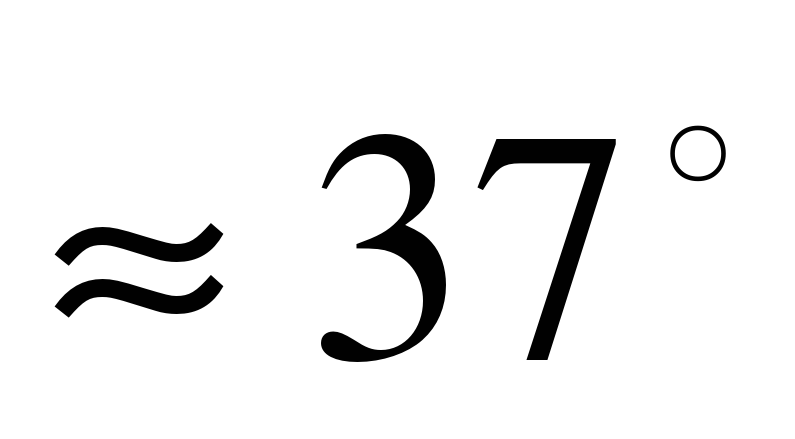
Воспользуемся формулой. Подставляя в неё значения k₁=2 и k₂= , находим tg===

=arctg);

Подставим значения А₁ = 2, В₁=-3,А₂=5,В₂=-1 в формулу : tg==1,

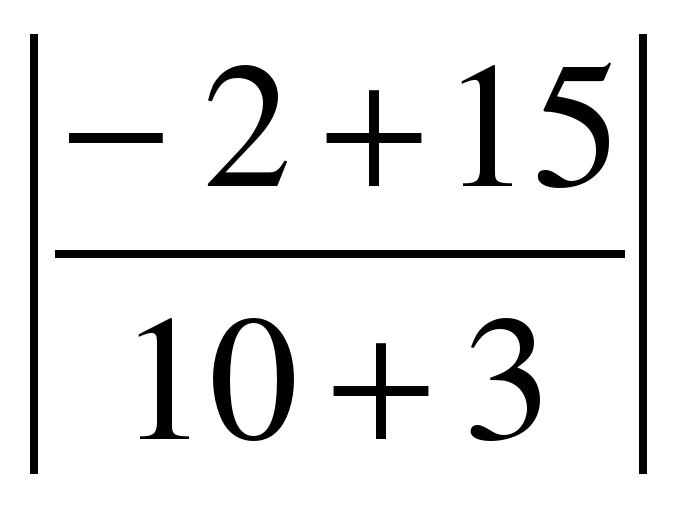
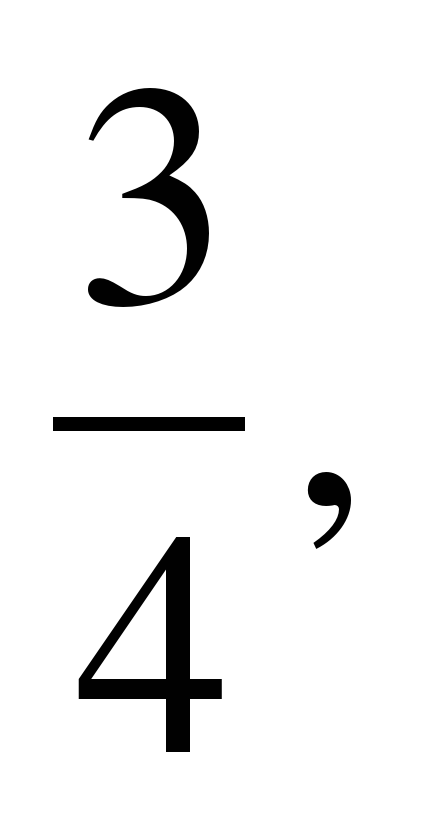
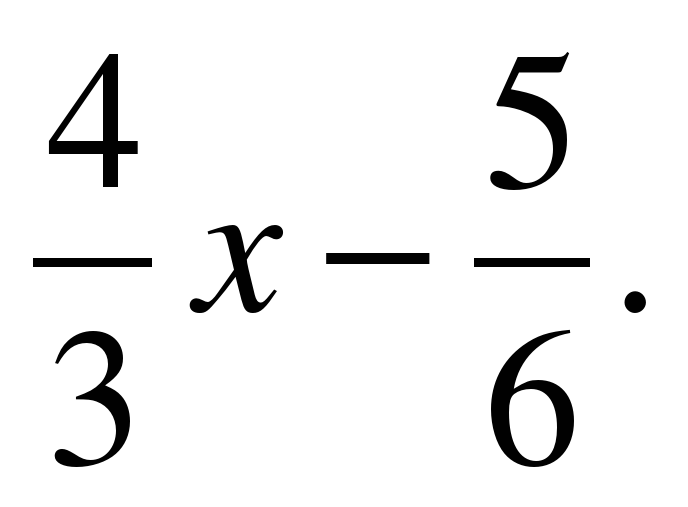
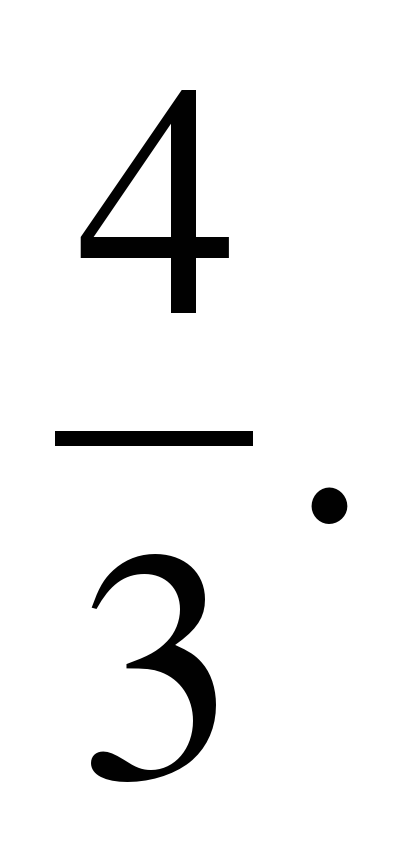
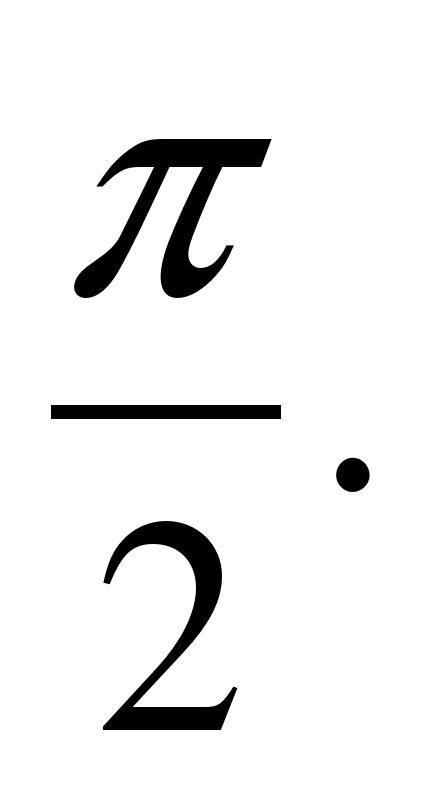
Здесь k₁=найдём k₂. Для этого перейдём от 6y =-8x-5 к эквивалентному равенству y=- Здесь k₂=-Так как k₁*k₂=-1, то данные прямые перпендикулярны. (По формуле получаем:tg==)

k₁=5,k₂=5, tg=0,=0.

Задания для практических занятий:

1. Найти угол между прямыми:

2) 2х-3у-7=0 и 2х-у+5=0;

3) у=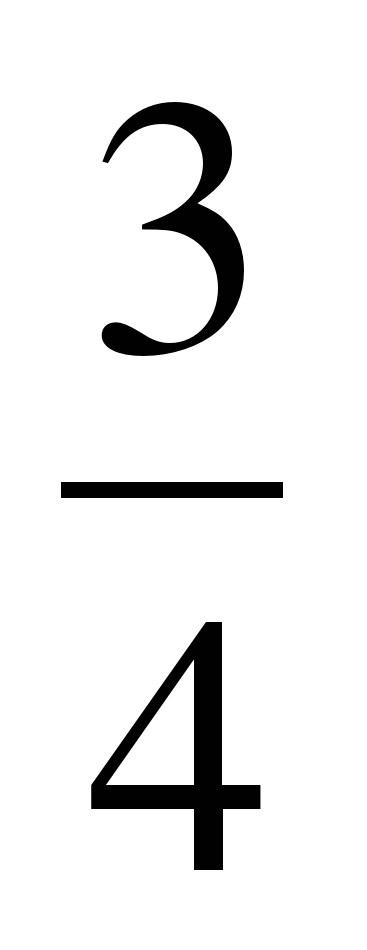х+6 и 3х-2у-8=0;

4) у= 7х -1 и у=7х+1;

2. Исследовать взаимное расположение следующих пар прямых:

1) 3х+5у-9=0 и 10х-6у+4=0

2) 2х+5у-2=0 и х+у+4=0;

3) 2у=х-1 и 4у-2х+2=0;

5) =1 и у=х+2;

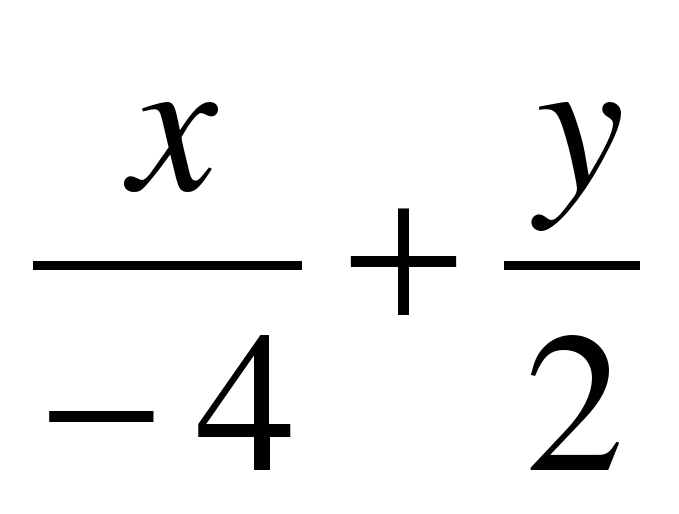
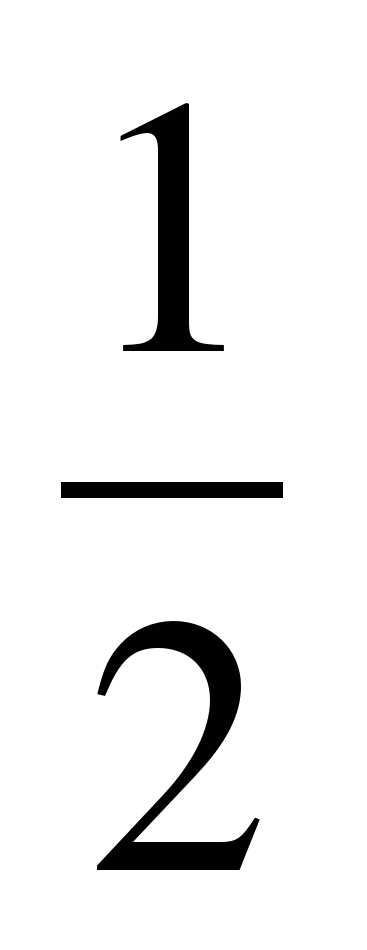
8) у=3-6х и 12х+2у-5=0;

10) х —у-1=0 и х +у+2=0

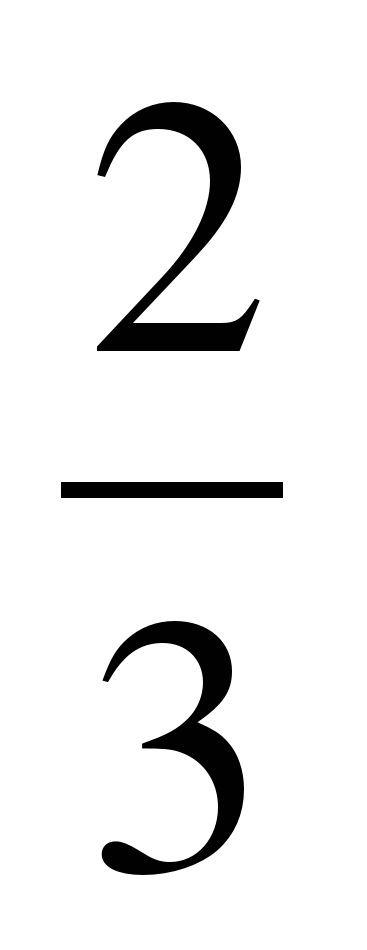
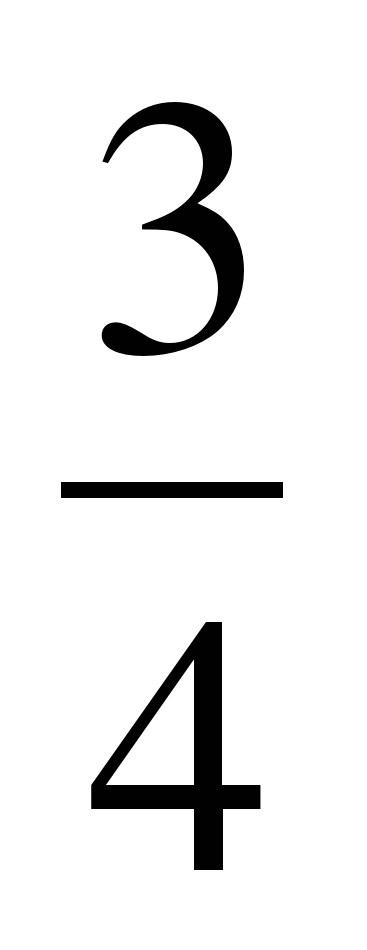
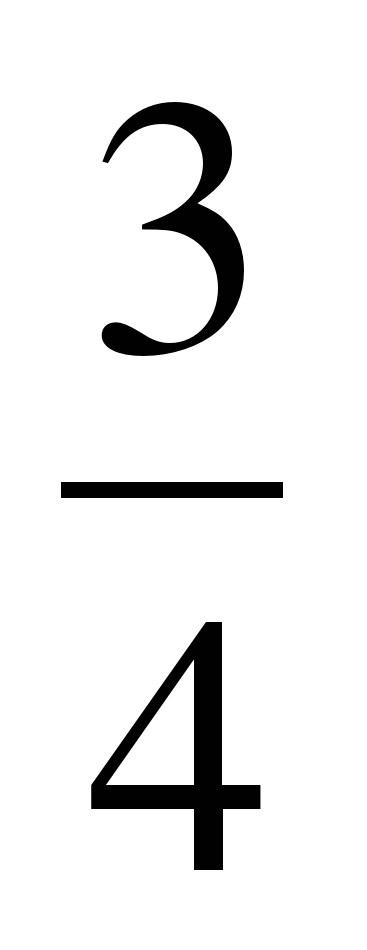
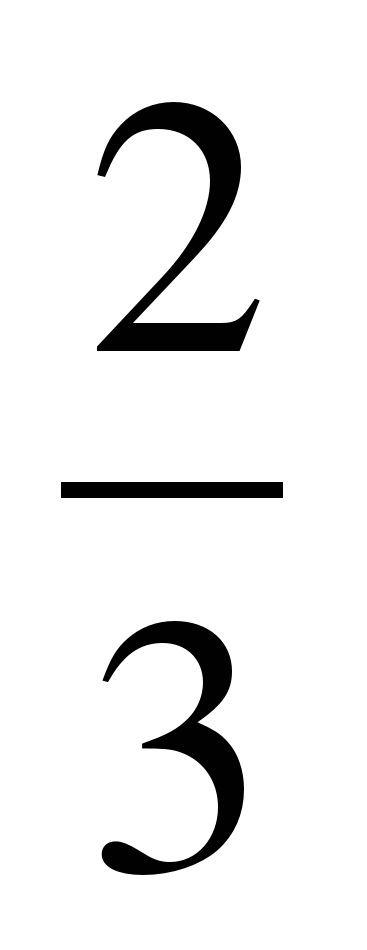
3. При каких значениях следующие пары прямых: а) параллельны; б) перпендикулярны.

1) 2х-3у+4=0 и х-6у+7=0;

2) х-4у+1=0 и -2х+у+2=0;

3) 4х+у-6=0 и 3х+у-2=0;

4) х- у+5=0 и 2х+3у+3=0;

4.Через точку пересечения прямых 3х-2у+5=0; х+2у-9=0 проведена прямая, параллельная прямой 2х+у+6=0. Составить ее уравнение.

5. Найти уравнение прямой, проходящий через точку А (-1;2):

а) параллельно прямой у=2х-7;

б) перпендикулярно прямой х+3у-2=0.

6. Найти длину высоты ВД в треугольнике с вершинами А (4;-3); В (-2;6) и С (5;4).

7. Даны уравнения сторон треугольника: х+3у-3=0, 3х-11у-29=0 и 3х-у+11=0.

Найти вершины этого треугольника.

Задания для самостоятельного решения

1. Найти острый угол между прямыми:

2) 2х-3у+6=0 и 3х-у-3=0

4) 3х+4у-12=0 и 15х-8у-45=0

2. Исследовать взаимное расположение следующих пар прямых:

1) 2х-3у+4=0 и 10х+3у-6=0

2) 3х-4у+12=0 и 4х+3у-6=0

3) 25х+20у-8=0 и 5х+4у+4=0

4) 4х+5у-8=0 и 3х-2у+4=0

3. Найти уравнение прямой, проходящий через точку В (2;-3)

а) параллельно прямой, соединяющей точки М₁ (-4;0) и М₂ (2;2);

б) перпендикулярно прямой х-у=0.

4. Составить уравнение прямой, содержащий высоту ВД в треугольнике с вершинами

А (-3;2), В (5;-2), С (0; 4)

5. Найти площадь треугольника, образованного прямыми 2х+у+4=0, х+7у-11=0 и 3х-5у-7=0.

6.Через точку пересечения прямых 3х+2у-4=0 и х-5у+8=0 проведены прямые, одна из которых проходит через начало координат, а другая параллельна оси Ох. Составить их уравнения.

7. Дан четырехугольник АВСД с вершинами А (3;5); В (6;6); С (5;3); Д (1;1). Найти:

а) координаты точки пересечения диагоналей;

б) угол между диагоналями.

8.Даны вершины треугольника А(2;-2), В (3;5), С (6;1). Найти:

1) длины сторон АС и ВС;

2) уравнения прямых, на которых лежат стороны ВС и АС;

3) уравнение прямой , на которой лежит высота, проведенная из В;

4) длину этой высоты;

5) уравнение прямой, на которой лежит медиана проведенная из точки А;

6) длину этой медианы;

7) уравнение прямой, на которой лежит биссектриса угла С;

8) центр тяжести треугольника;