Содержание:
В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.
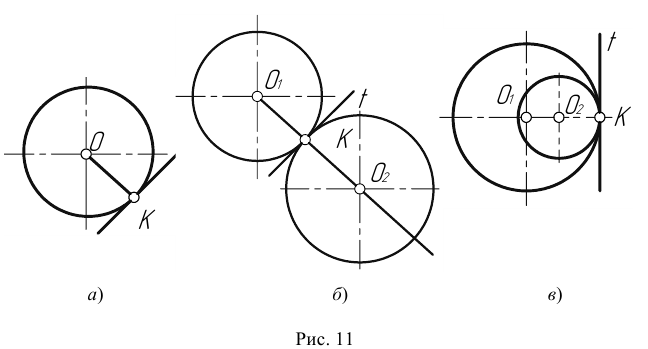
- Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
- Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).
Точка касания К и центры окружностей
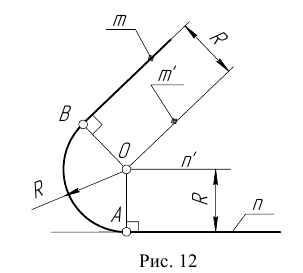
- Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
- Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
- Дуга сопряжения АВ – это дуга окружности, с помощью которой выполняется сопряжение (рис. 12).
- Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).
Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.
- Сопряжение двух пересекающихся прямых линий
- Сопряжения прямой с окружностью
- Сопряжение двух окружностей
- Построение касательных
- Методическое пособие: ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ. (Деление окружности на части; Сопряжения; Локальные кривые; Конусность, уклон.)
- Правила построения сопряжений и деления окружностей на равные части
- 📸 Видео
Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение двух пересекающихся прямых линий
Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.
Выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от прямой n на расстояние радиуса R сопряжения. Таким множеством является прямая
параллельная данной прямой n и отстоящая от неё на расстояние R.
- Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения. Таким множеством является прямая
параллельная m и отстоящая от последней на расстояние R.
- В пересечении построенных прямых
найдем центр сопряжения О.
- Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.
Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.
Видео:ВСЯ СУТЬ СОПРЯЖЕНИЙ И ПЕРЕХОДОВ. Правило построения сопряжений. Геометрические построенияСкачать

Сопряжения прямой с окружностью
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.
Пример 1. Пусть задана окружность радиусом R с центром в точке 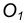
Для решения задачи выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая
параллельная m и отстоящая от неё на расстояние R.
- Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность
проведенная радиусом
- Центр сопряжения О находим как точку пересечения линий
- Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
- Проведем дугу сопряжения АВ.
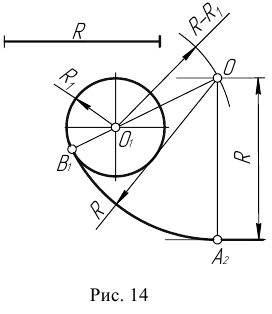
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 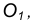
Видео:Деление окружностей на равные частиСкачать
Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 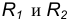
- Для нахождения центра сопряжения О проведем окружность
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
равен
- Радиусом
проведем окружность
, удаленную от данной окружности n на расстояние R.
- Найдем центр сопряжения О как точку пересечения окружностей
.
- Найдем точку сопряжения А как пересечение линии центров
с дугой m.
- Аналогично найдем точку В как пересечение линии центров
с дугой n .
- Проведем дугу сопряжения АВ.
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами 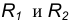
- Для нахождения центра сопряжения О проведем окружность
на расстоянии
от данной окружности m.
- Проведем окружность
на расстоянии
от данной окружности n.
- Центр сопряжения О найдем как точку пересечения окружностей
- Точку сопряжения А найдем как точку пересечения линии центров
с заданной окружностью m.
- Точку сопряжения В найдем как точку пересечения линии центров
c заданной окружностью n.
- Проведем дугу сопряжения AВ с центром в точке O.
Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.
Видео:Видеоуроки по КОМПАС 3D. Урок 1 Деление окружности на равные частиСкачать

Построение касательных
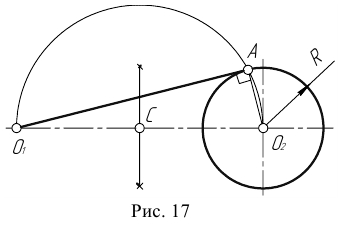
Пример 1. Дана окружность с центром в точке 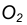
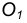
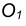
Для решения задачи выполним следующие построения.
- Соединим точку
с центром окружности
- Находим середину С отрезка
- Из точки С, как из центра, проведем вспомогательную окружность радиусом
- В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку
с точкой А.
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 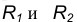
- Находим середину С отрезка
- Из точки С, как из центра, радиусом
проведем вспомогательную окружность.
- Из центра большей окружности
проведем вторую вспомогательную окружность радиусом
- Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус
идущий в точку касания В. 5. Для построения второй точки касания А проведем
- Соединим точки А и В отрезком прямой линии.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Нанесение размеров на чертежах
- Резьба на чертеже
- Соединения разъемные и неразъемные в инженерной графике
- Виды конструкторских документов
- Виды в инженерной графике
- Разрезы в инженерной графике
- Сечения в инженерной графике
- Выносные элементы в инженерной графике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:1 2 4 сопряжение окружностейСкачать

Методическое пособие: ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ. (Деление окружности на части; Сопряжения; Локальные кривые; Конусность, уклон.)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
ГБПОУ ВО «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПРОМЫШЛЕННО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»
Практическая работа №3
Деление окружности на части;
ДЕЛЕНИЕ ОКРУЖНОСТИ НА ЧАСТИ……………………. 3
ВЫПОЛНЕНИЕ СОПРЯЖЕНИЙ……………………………. 5
УКЛОН И КОНУСНОСТЬ……………………………………. 12
ЗАДАНИЕ К ПРАКТИЧЕСКОЙ РАБОТЕ………………….…..15
ПРАКТИЧЕСКАЯ РАБОТА №3
Тема: Деление окружности на равные части. Сопряжении. Локальные кривые. Конусность, уклон.
Цель: 1) Ознакомление с правилами деления окружности на равное количество частей, а также приобретение ими навыков вычерчивания детали с применением деления окружности.
2) Научится выполнять различные виды сопряжений.
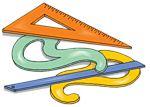
ДЕЛЕНИЕ ОКРУЖНОСТИ НА ЧАСТИ
Некоторые детали машин и приборов имеют элементы, равномерно расположенные по окружности. При выполнении таких деталей необходимо знать правила деления окружности на равное количество частей.
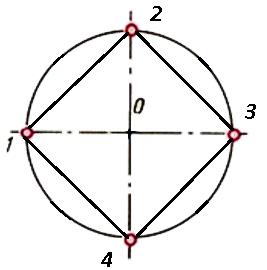
1. Деление окружности на четыре равные части и построение правильного вписанного четырехугольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части в соответствии с рисунком 1. Соединив точки пересечения этих линий с окружностью прямыми, получим правильный вписанный четырехугольник.
Рис. 1 Деление на четыре части, восемь частей.
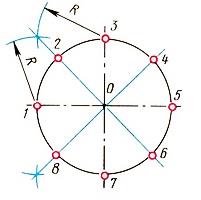
2. Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника. Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 в соответствии с рисунком 2. Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.
Если полученные точки соединить последовательно прямыми линиями, то получится правильный восьмиугольник
Рис. 2 Деление окружности на восемь равных частей.
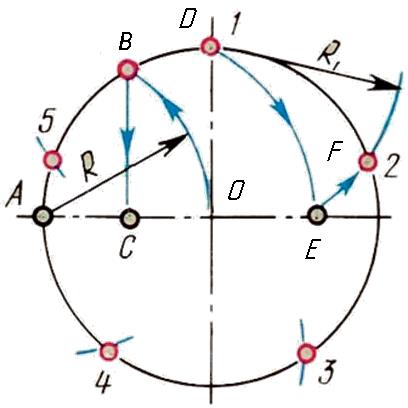
3. Деление окружности на три равные части и построение правильного вписанного треугольника. Данные построения выполняют с помощью циркуля или угольника с углами 30, 60 и 90 и рейсшины.
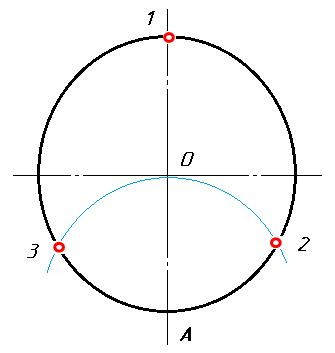
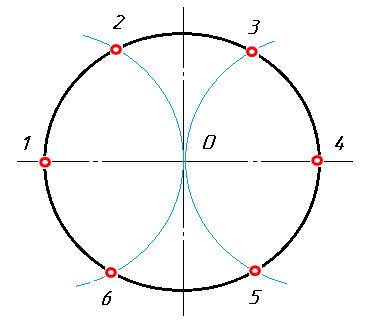
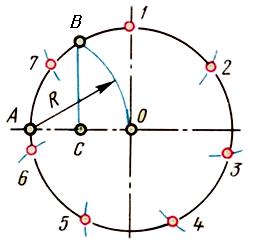
При делении окружности циркулем на три равные части из любой точки окружности, например из точки А пересечения центровых линий с окружностью, в соответствии с рисунком 3, проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку А.
Рис. 3 Деление окружности циркулем на три равные части.
Последовательно соединив точки 1, 2 и 3, получим правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин (например, точка 1), находят точку А. Для этого через заданную точку 1 проводят диаметр , рисунок 3 в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R, равным радиусу данной окружности, и получают точки 2 и 3.
4. Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника. При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5.
Последовательно соединив полученные точки, получим правильный вписанный шестиугольник в соответствии с рисунком 4.
Рис. 4 Деление окружности на шесть равных частей
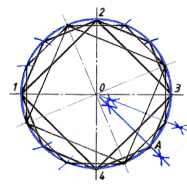
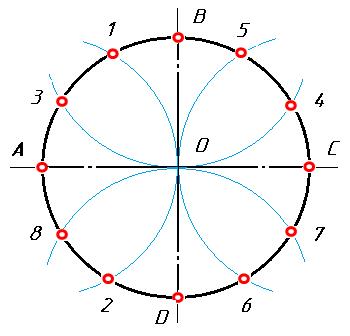
5. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника. При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью в соответствии с рисунком 5, а. Соединив полученные точки, получают правильный вписанный двенадцатиугольник в соответствии с рисунком 5,б.
Рис. 5 — Деление окружности на двенадцать равных частей.
Сопряжение – это плавный переход одной линии в другую.
Центр сопряжения: это точка пересечения вспомогательных прямых (дуг окружности), параллельных сопрягаемым прямым (окружностям) и проведенным на расстоянии R от них.
Точки сопряжения : это точки, находящиеся на пересечении перпендикуляров, проведенных из центра сопряжения к сопрягаемым сторонам.
Сопряжение пересекающихся прямых дугой окружности данного радиуса
1.Провести две линии центров параллельно каждой на расстоянии, равном радиусу R дуги сопряжения (рис. 6). Точка их пересечения будет центром дуги сопряжения.
2. Из центра сопряжения O провести перпендикуляры на заданные прямые и получить точки сопряжения К и .
3. Из точки О радиусом R провести дугу сопряжения.
Рис. 6 Сопряжение окружности и прямой линии дугой заданного радиуса R.
1. Из центра O данной окружности радиуса R провести дугу вспомогательной окружности радиуса R + R 1.
2. Провести прямую, параллельную заданной, на расстоянии R 1. Точка пересечения проведенной прямой и дуги вспомогательной окружности будет центром дуги сопряжения О1 .
3. Соединить найденный центр O 1 и центр окружности О и получить точку сопряжения К.
4. Опустить перпендикуляр с центра дуги окружности О1 на заданную прямую и получить точку сопряжения K 1.
5. Из точки O 1 радиусом R 1 провести дугу сопряжения.
Рис. 7. Внешнее сопряжение окружности с прямой линией
Внутреннее касание (рис.8):
1. Из центра О данной окружности радиуса R провести дугу вспомогательной окружности радиуса R — R 1.
2. Провести прямую, параллельную заданной, на расстоянии R 1. Точка пересечения проведенной прямой и дуги вспомогательной окружности будет центром дуги сопряжения O 1.
3. Соединить найденный центр O 1 и центр окружности О и получить точку сопряжения К.
4. Опустить перпендикуляр с центра дуги окружности О1 на заданную прямую и получить точки сопряжения R 1.
5. Из точки O 1 радиусом R 1 провести дугу сопряжения.
Рис. 8. Внутреннее сопряжение окружности с прямой линией.
Сопряжение двух окружностей дугой заданного радиуса R 3.
Из центра O1 данной окружности радиуса R 1 провести дугу ( R 1+ R 3) вспомогательной окружности радиуса
2. Из центра О2 данной окружности радиуса R 2 провести дугу ( R 2 + R 3) вспомогательной окружности радиуса. Точка пересечения этих вспомогательных дуг окружности будет центром дуги сопряжения O 3.
3.Соединить найденный центр и центр O 3 окружности О1 и получить точку сопряжения К.
4.Соединить найденный центр О3 и центр окружности О2. и получить точку сопряжения М.
5. Из точки O 3 радиусом R 3 провести дугу сопряжения.
Внутреннее касание (рис. 10):
1.Из центра О1 данной окружности радиуса R 1 провести дугу ( R 3- R 1) вспомогательной окружности радиуса
2.Из центра О2 данной окружности радиуса R 2 провести дугу ( R 3- R 2) вспомогательной окружности радиуса. Точка пересечения этих вспомогательных дуг окружности будет центром дуги сопряжения .
3. Соединить найденный центр O 3 и центр окружности О2 и получить точку сопряжения К.
4.Соединить найденный центр О3 и центр окружности О2. и получить точку сопряжения М.
5. Из точки O 3 радиусом R 3 провести дугу сопряжения.
Смешанное касание (внешнее и внутреннее) (рис. 11):
1.Из центра O 1 данной окружности радиуса R 1 провести дугу ( R 3- R 1) вспомогательной окружности радиуса
2. Из центра О2 данной окружности радиуса R 2 провести дугу ( R 3 + R 2) вспомогательной окружности радиуса. Точка пересечения этих вспомогательных дуг окружности будет центром дуги сопряжения .
3.Соединить найденный центр O 3 и центр окружности O 1 и получить точку сопряжения К.
4.Соединить найденный центр О3 и центр окружности О2 и получить точку сопряжения М.
5. Из точки O 3 радиусом R 3 провести дугу сопряжения.
Так называемые лекальные кривые — это кривые, которые не могут быть точно составлены из дуг окружностей.
Обычно при построении лекальной кривой, зная закономерность ее образования, на чертеже наносят ряд принадлежащих ей точек, которые затем соединяют плавной линией при помощи лекала. Обратите внимание, что прежде чем обводить кривую по лекалу, следует наметить от руки форму кривой. Подбирая положение лекала, возможно плотнее прилегающее к данной кривой, обводят не весь участок, а только часть его (рис. 7.3а). Необходимо, чтобы новое положение лекала несколько перекрывало предыдущее.
Рассмотрим наиболее часто встречающиеся в практике чертежных работ лекальные кривые.
Э л л и п с. Пусть даны размеры большой MN и малой DЕ осей эллипса (рис. 7.3б).
Для построения эллипса проводят две концентрические окружности, диаметры которых равны осям эллипса. Эти окружности делят на 12 равных частей. Через точки деления на большой окружности проводят вертикальные линии, через соответствующие точки деления на малой окружности ¾ горизонтальные линии. Пересечение этих линий даст точки эллипса I, II, III. Если из точки D (или Е) провести дугу радиусом R = MN/2, то на большой оси эллипса будут получены его фокусы (точки F1 и F2).
При обводке эллипса можно подобрать лекало так, чтобы оно охватывало 1/4 часть его. Рекомендуется при обводке эллипса и других симметричных кривых делать на лекале засечки-черточки карандашом и прикладывать этот участок лекала к симметричной части кривой.
Парабола. Пусть даны вершина параболы О, одна из точек параболы D и направление оси OC (рис. 7.3в). На отрезках ОС и CD строят прямоугольник, стороны этого прямоугольника OB и BD делят на одинаковое число равных частей и нумеруют точки деления. Вершину О соединяют с точками деления стороны BD, а из точек деления отрезка OB проводят прямые, параллельные оси. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяет ряд точек параболы.
Циклоида (рис. 7.4а). Траектория точки А, принадлежащей окружности радиуса R , перекатываемой без скольжения по прямой, называется циклоидой. Для ее построения от исходного положения точки А на направляющей прямой откладывают отрезок АА 1 , равный длине данной окружности 2R. Окружность и отрезок АА 1 делят на одинаковое число равных частей.
Восстанавливая перпендикуляры из точек деления прямой АА 1 до пересечения с прямой, проходящей через центр данной окружности параллельно АА 1 , намечают ряд последовательных положений центра перекатываемой окружности О 1 , О 2 , О 3 , … О 8 .
Описывая из этих центров окружности радиуса R, отмечают точки пересечения с ними прямых, проходящих параллельно АА 1 через точки деления окружности 1, 2, 3, 4 и т. д.
В пересечении горизонтальной прямой, проходящей через точку 1, с окружностью, описанной из центра О 1 , находится одна из точек циклоиды; в пересечении прямой, проходящей через точку 2, с окружностью, проведенной из центра О 2 , находится другая точка циклоиды и т. д.
Синусоида (рис. 7.4 б). Для построения синусоиды делят окружность заданного радиуса R на равные части (6, 8, 12 и т. д.) и на продолжении осевой линии от условного начала точки А проводят отрезок прямой АВ, равный 2R. Затем прямую делят на такое же число равных частей, что и окружность (6, 8, 12 и т. д.). Из точек окружности 1, 2, 3, . 12 проводят прямые линии параллельно выбранной прямой до пересечения с соответствующими перпендикулярами, восстановленными или опущенными из точек деления прямой.
Полученные точки пересечения (1, 2, 3, . 12) и будут точками синусоиды с периодом колебаний, равным 2R.
Эвольвента (развертка круга). Эвольвентой (рис. 7.4в) называется траектория, описываемая точкой прямой линии, перекатываемой по окружности без скольжения.
В машиностроении по эвольвенте очерчивают профиль головок зубьев зубчатых колес.
Для построения эвольвенты окружность радиуса R предварительно делят на произвольное число n равных частей; в точках деления проводят касательные к окружности, направленные в одну сторону. На касательной, проведенной через последнюю точку деления, откладывают отрезок, равный длине окружности 2R, и делят его на то же число n равных частей.
Откладывая на первой касательной одно деление, равное 2R, а на второй два, на третьей три и т. д., получают ряд точек I, II, III, IV и т. д., которые соединяют по лекалу.
УКЛОН И КОНУСНОСТЬ
Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
Уклон – наклон одной прямой линии к другой (рис.15).
Уклон i прямой АС определяется из прямоугольного треугольника АВС как отношение противолежащего катета ВС к прилежащему катету АС (рис.2):
Уклон может быть выражен в процентах (например, уклон в 10%
внутренних граней полок швеллера по ГОСТ 8240-89,рис. 17), отношением двух чисел (например, уклоны 1:20 и 1:4 граней рельса по ГОСТ8168-75*)или в промилях (например, уклон 5‰ арматуры).
Знак уклона “ “, вершина которого должна быть направлена в сторону уклона, наносят перед размерным числом, располагаемым непосредственно у изображения поверхности уклона, или на полке линии – выноски, как показано на рисунках.
Провести прямую с уклоном i = 1:6 относительно прямой АЕ через точку А, лежащую на прямой АЕ (рис.17). Отложим на прямой АЕ от точки А шесть произвольно выбранных единиц. Через полученную точку В восстановим перпендикуляр к АЕ длиной в одну единицу. Гипотенуза АС построенного прямоугольного треугольника АВС является искомой прямой с уклоном 1:6.
Построение полок швеллера и двутавра
На рис. 18 и 19 показано построение уклона внутренней грани верхней полки швеллера и двутавра. Построен вспомогательный треугольник ВСD с катетами 10 и 100мм для швеллера и 12 и 100мм для двутавра.
На горизонтальном отрезке «b» отложим отрезок, равный (b-d)/2– для швеллера и(b-d)/4– для двутавра. Из полученной точки проведем перпендикуляр длиной t. Отложенные размеры определили положение точки К, через которую проходит прямая с уклоном 10% для швеллера и 12% — для двутавра. Через точку К провести прямую, параллельную гипотенузе построенного треугольника.
Конусностью называется отношение диаметра окружности основания D прямого конуса к его высоте h (рис.20).
Для усеченного кругового конуса – отношение разности диаметров двух нормальных сечений конуса к расстоянию между ними (рис.21), т.е.
Конусность, как и уклон, может быть выражена отношением целых чисел или в процентах. Перед размерным числом, характеризующим конусность, наносят знак “ ”, острый угол которого должен быть направлен в сторону вершины конуса.
При одном и том же угле конусность в два раза больше уклона, так как уклон образующей конуса равен отношению радиуса его основания к высоте, а конусность – отношению диаметра к высоте.
Таким образом, построение конусности i : n относительно данной оси сводится к построению уклонов i : 2n с каждой стороны оси.
Вычертить контуры деталей, применяя правила построения сопряжений и навыки деления окружностей на равные части. Задание выполнить на формате А3
Вариант задания получить у преподавателя.
Что называют сопряжением? В какой последовательности выполняют сопряжения, если известен радиус дуги сопряжения и сопрягаемые линии?
Как определяют точки касания при сопряжении двух окружностей с помощью дуги окружности?
Назовите стандартные масштабы увеличения и уменьшения, установленные ГОСТ.
Назовите типы сопряжений и опишите принцип их построения.
Что такое уклон? Как определить уклон?
Как построить уклон? Обозначение уклона на чертежах по ГОСТ.
Что такое конусность?
Формула для расчёта конусности. Обозначение конусности на чертежах.
Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Правила построения сопряжений и деления окружностей на равные части
Раздел 3: Чтение и выполнение чертежей (7 часов)
Выполнение чертежей предметов с использованием геометрических построений (деление окружности на равные части, деление углов и отрезков на равные части; сопряжения). Общее понятие о форме и формообразовании предметов. Анализ геометрической формы предметов. Способы чтения и выполнения чертежей на основе анализа формы. Построение третьей проекции предмета по двум заданным. Нахождение на чертеже вершин, ребер и граней, поверхностей геометрических тел, составляющих форму предмета. Определение необходимого и достаточного количества видов на чертеже. Творческие задачи на пройденный материал.
Урок № 11: Деление окружности на равные части
 Предыдущий урок Предыдущий урок |  Поурочное планирование Поурочное планирование  | Следующий урок  |
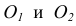
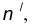 параллельная данной прямой n и отстоящая от неё на расстояние R.
параллельная данной прямой n и отстоящая от неё на расстояние R.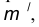 параллельная m и отстоящая от последней на расстояние R.
параллельная m и отстоящая от последней на расстояние R.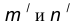 найдем центр сопряжения О.
найдем центр сопряжения О.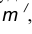 параллельная m и отстоящая от неё на расстояние R.
параллельная m и отстоящая от неё на расстояние R.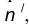 проведенная радиусом
проведенная радиусом 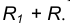
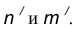
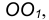 т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.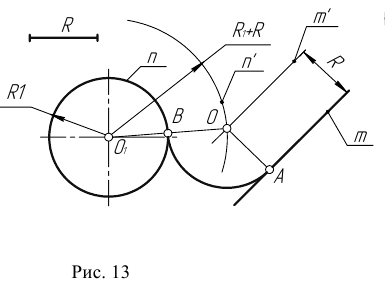
 удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности 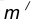 равен
равен 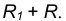
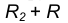 проведем окружность
проведем окружность 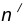 , удаленную от данной окружности n на расстояние R.
, удаленную от данной окружности n на расстояние R.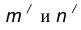 .
.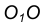 с дугой m.
с дугой m.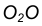 с дугой n .
с дугой n .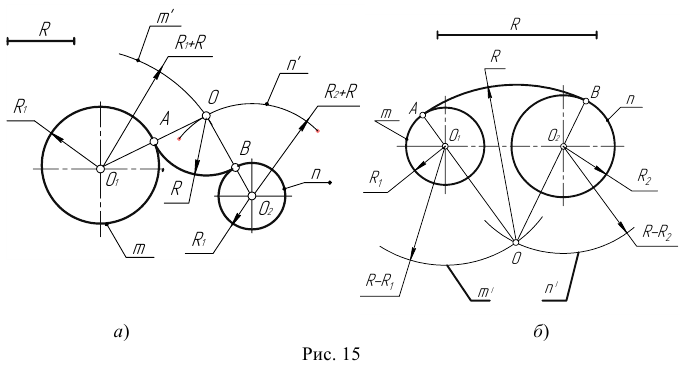
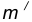 на расстоянии
на расстоянии 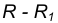 от данной окружности m.
от данной окружности m.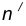 на расстоянии
на расстоянии 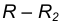 от данной окружности n.
от данной окружности n.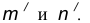
 с заданной окружностью m.
с заданной окружностью m. c заданной окружностью n.
c заданной окружностью n.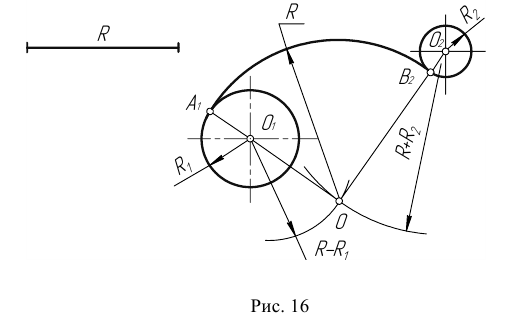
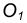 с центром окружности
с центром окружности 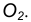
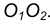
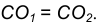
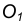 с точкой А.
с точкой А.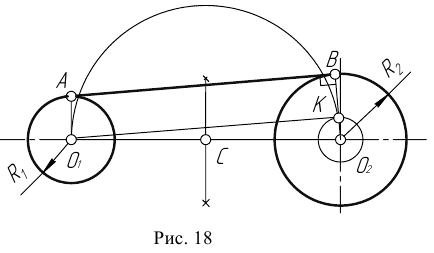
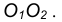
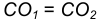 проведем вспомогательную окружность.
проведем вспомогательную окружность.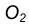 проведем вторую вспомогательную окружность радиусом
проведем вторую вспомогательную окружность радиусом 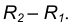
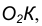 идущий в точку касания В. 5. Для построения второй точки касания А проведем
идущий в точку касания В. 5. Для построения второй точки касания А проведем 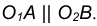




















 pdf Проведение параллельных прямых
pdf Проведение параллельных прямых