- Задача
- Похожие задачи
- Решение
- Калькулятор матриц — действия с матрицами онлайн
- Как пользоваться калькулятором матриц
- Ввод данных и функционал
- Что умеет наш калькулятор матриц?
- Вычисление выражений с матрицами
- Из чего могут состоять выражения?
- Примеры корректных выражений
- Что такое матрица?
- Примеры матриц
- Элементы матрицы
- Некоторые теоретические сведения
- Калькулятор матриц
- Описание калькулятора матриц
- 💡 Видео
Задача
Вариант 1. Найти сумму элементов каждой строки матрицы (двумерного массива).
Вариант 2. Вычислить сумму элементов определенной строки матрицы.
Похожие задачи
Решение
Если поставлена задача вычислить сумму элементов каждой строки матрицы, то алгоритм ее выполнения таков:
- По-строчно перебираем элементы матрицы (внешний цикл отвечает за переход к новой строке, счетчик — первый индекс элементов).
- Во внешнем цикле перед внутренним присваиваем переменной для суммы значение 0. В ней будет накапливаться сумма элементов текущей строки, элементы которой перебираются во внутреннем цикле.
- После внутреннего цикла выводим значение переменной-суммы на экран.
Ниже в примере решения данной задачи заполнение матрицы, вывод элементов на экран и подсчет суммы выполняются внутри одного цикла. Это сделано не только для сокращения кода программы, но и для красивого вывода. После того, как выводятся элементы очередной строки, в конце этой же строки выводится их сумма.
Если поставлена задача нахождения суммы элементов только определенной строки матрицы, то в решении используется только один цикл (без вложенного). Перебираются только элементы указанной строки. При этом меняется значение только второго индекса, а первый всегда постоянен — это номер строки.
Программа ниже усложнена тем, что пользователь сам определяет номер строки матрицы, элементы которой необходимо просуммировать. Если поставлена задача, в которой конкретно задается строка, то вместо переменной num следует использовать число, обозначающее номер строки. Например, для третьей строки выражение sum : = sum + mat [ num , j ] следует заменить на sum : = sum + mat [ 3 , j ] .
Видео:Ранг матрицыСкачать

Калькулятор матриц — действия с матрицами онлайн
С помощью калькулятора матриц вы сможете выполнять различные преобразования матриц, решать СЛАУ, а также находить некоторые характеристики, как, например, определитель, след и ранг. Подробнее о функционале и использовании калькулятора смотрите после блока с самим калькулятором.
Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: a T ij = aji
Видео:Как разложить вектор по базису - bezbotvyСкачать

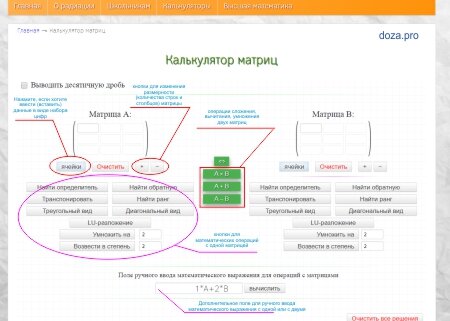
Как пользоваться калькулятором матриц
- Выберите матрицу (или матрицы) с помощью переключателей ( )
- Укажите размер с помощью выпадающих списков под матрицей ( × )
- Заполните элементы (нулевые элементы можно не заполнять.)
- Выберите в выпадающем списке требуемую функцию и, если требуется, введите дополнительные параметры.
- Нажмите кнопку .
- Если вывод чисел не устраивает, просто поменяйте его — доступны три варианта представления: правильные дроби (2
Видео:Матрицы и векторыСкачать

Ввод данных и функционал
- В качестве элементов используются обыкновенные правильные дроби ( 1/2 , 29/7 , -1/125 ), десятичные дроби ( 12 , -0.01 , 3.14 ), а также числа в экспоненциальной форме ( 2.5e3 , 1e-2 ).
- Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
- Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
- Вставляйте результат в A или B с помощью кнопок «Вставить в A» и «Вставить в B».
- Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
- Используйте стрелки ( ← , ↑ , → , ↓ ) для перемещения по элементам
Видео:Собственные векторы и собственные значения матрицыСкачать

Что умеет наш калькулятор матриц?
Видео:Найдите разложение вектора по векторам (базису)Скачать

Вычисление выражений с матрицами
Вы можете вычислять различные арифметические выражения с матрицами, а также с результатами некоторых преобразований этих матриц.
Из чего могут состоять выражения?
- Целые и дробные числа
- Матрицы A, B
- Знаки арифметических действий: + — * /
- Круглые скобки для изменения приоритета операций: ( )
- Транспонирование: ^T
- Возведение в целую степень: ^
Примеры корректных выражений
- Cложение двух матриц: A+B , (A)+(B) , ((A) + B)
- Возведение линейной комбинации матриц в степень: (3A — 0.5B)^5
- Произведение транспонированной матрицы на исходную: A^TA
- Обратная матрица в квадрате для B: B^-2
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Что такое матрица?
Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами. Матрицы обозначаются заглавными латинскими буквами. При необходимости размер записывается следующим образом: An×m .
Примеры матриц
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
| 2 | -1 | 0 | 0 |
| -3 | 2 | 0 | 0 |
| 31 | -19 | 3 | -4 |
| -23 | 14 | -2 | 3 |
Элементы матрицы
Элементы A обозначаются aij , где i — номер строки, в которой находится элемент, j — номер столбца.
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Некоторые теоретические сведения
Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: a T ij = aji
Главная диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы. Элементы главной диагонали — aii
Единичная матрица En×n — квадратная матрица из n столбцов и n строк с единицами на главной диагонали и нулями вне её.
Ранг — это максимальное количество линейно независимых строк (столбцов) этой матрицы. Обозначение: rank(A)
След — это сумма элементов, находящихся на её главной диагонали. Обозначение: tr(A) или track(A)
Умножение матрицы на число — матрица такой же размерности, что и исходная, каждый элемент которой является произведением соответствующего элемента исходной матрицы на заданное число.
Возведение в степень — умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу. Обозначение: A n
Обратная матрица A −1 — матрица, произведение которой на исходную матрицу A равно единичной матрице: A -1 ×A = A×A -1 = E
Треугольная матрица — квадратная матрица, у которой выше (верхнетреугольная матрица) или ниже (нижнетреугольная матрица) главной диагонали находятся нули.
LU-разложение — представление матрицы в виде произведения двух матриц L и U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. A = L·U
Сложение матриц An×m и Bn×m — матрица Cn×m, получаемая попарной суммой соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij+bij
Разность матриц An×m и Bn×m — матрица Cn×m, получаемая попарной разностью соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij-bij
Умножение матриц An×k и Bk×m — матрица Cn×m, у которой элемент (cij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B: cij = ai1·b1j + ai2·b2j + . + aik·bkj
Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.
Видео:5 способов вычисления определителя ★ Какой способ лучше?Скачать

Калькулятор матриц
Калькулятор матриц для пошагового решения матриц с последовательностью решения, бесплатно в режиме онлайн. Для всех вычислений приводятся пояснения и ссылки на необходимую теорию.
Поле ручного ввода математического выражения для операций с матрицами
Матричный калькулятор позволяет выполнить умножение матриц, сложение и вычитание матриц, найти ранг, вычислить определитель, осуществить транспонирование матрицы, найти обратную матрицу, а также выполнить другие операции с матрицами.
Наш калькулятор поможет выполнить математические операции с матрицами или проверить уже выполненные самостоятельно вычисления.
Видео:Лекция 2, Векторные и матричные нормы, унитарные матрицы, SVDСкачать

Описание калькулятора матриц
Используя калькулятор матриц, вы сможете выполнить необходимые вычисления с матрицами, получив в результате требуемый ответ и подробную последовательность решения. Матричный калькулятор позволяет выполнять операции с одной матрицей или решать сложные выражения сразу с несколькими матрицами.
Заполните поля для элементов матрицы и нажмите соответствующую кнопку.
- С помощью плюса и минуса выберите нужный размер матрицы. Если нужна неквадратная матрица, то просто ненужные ячейки оставьте пустыми.
- Внесите значение элементов матрицы в ячейки. Значения могут быть:
- целые числа: 7 , -3 , 0
- десятичные (конечные и периодические) дроби: 7/8 , 6.13 , -1.3(56) , 1.2e-4
- арифметические выражения: 1/2+3*(6-4) , (6-y)/x^3 , 2^0.5
- Нажмите на кнопку с названием нужной математической операции или в ручном режиме введите математическое выражение в специальное поле.
- Значения в результатах решения можно с помощью мышки перетаскивать на различные поля. Например, полученную матрицу можно перетащить на поле исходных данных, для дальнейшего решения.
💡 Видео
Матрицы: начало. Высшая математикаСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение матричных уравненийСкачать

Собственные векторы и собственные числа линейного оператораСкачать

Собственные значения и собственные векторыСкачать

МАТКАД МатрицыСкачать
Векторы и матрицы - часть 1Скачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Образуют ли данные векторы базисСкачать