Дана функция z f x y точка а и вектора найти grad z в точке (8 видео)

Как найти градиент

Решение находим с помощью калькулятора.
Градиент grad u

grad u в точке А

Вектор а(2;-1;0)
Направляющие углы

Модуль вектора |a| .

Производная в точке А по направлению вектора а .

Пример №2 . Найти grad u в точке М(0,0,0), если u=х*sin(z)-y*cos(z) .
Найти производную функции u=х*y 2 +z 3 -x*y*z в точке М(1,1,2) в направлении, образующем с осями координат углы соответственно в 60 о , 45 о , 60 о .

Пример №3 . Даны функция z = f(x,y) , точка A и вектор a . Найти: 1) наибольшую скорость возрастания функции в точке A ; 2) скорость изменения функции в точке A по направлению вектора a.
z = ln(x 2 + 3y 2 ), A(1,1), a(3,2).
Примечание: наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.
Скачать решение

Задача 1. Найти проекции grad z в точке М(1,2) , где z=ln(4x 2 -y).

Задача 2. Найти производную функции z=х 3 -3x 2 y +3xy 2 +1 в точке М(3,1) в направлении, идущем от этой точки к точке N(6,5) .

Задача 3. Даны функция z = f(x,y) , точка A(x₀,y₀) и вектор a(a₁,a₂). Найти:
1) grad z в точке A ;
2) производную в точке A по направлению вектора a .
Решение.
z = ln(5x 2 +3y 2 ), A(1;1), a(3;2)
Скачать решение

Содержание

Градиент функции онлайн
Производная по направлению, градиент функции: объяснение, примеры
Понятие производной по направлению
Примеры нахождения производной по направлению
Градиент функции
🔍 Видео

Видео:Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Градиент функции онлайн

Градиент функции — это вектор координатами которого являются частные производные этой функции по всем её переменным.

Градиент обозначается символом набла . Выражение градиента некоторой функции записывается следующим образом:

где , , — частные производные функции по переменным , , соответственно.

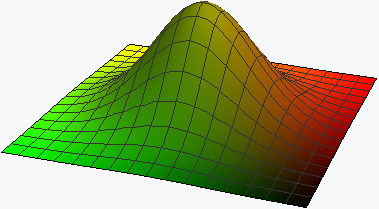
Вектор градиента указывает направление наискорейшего роста функции. Рассмотрим график функции .

Эта функция достигает своего единственного максимума в точке . График градиентного поля данной функции имеет вид:

Из данного градика видно, что в каждой точке вектор градиента направлен в сторону наискорейшего роста функции, т.е. в точку . При этом модуль вектора отражает скорость роста (крутизну подъёма) функции в этом направлении.

Задача вычисления градиента функции очень часто возникает при поиске эстремумов функции с использованием различных численных методов.

Наш онлайн калькулятор позволяет вычислить градиент практически любой функции как общем виде, так и в конкретной точке с описанием подробного хода решения на русском языке.

Видео:Градиент в точке.Скачать

Производная по направлению, градиент функции: объяснение, примеры

Видео:10. ФНП. Градиент и производная по направлению функции двух переменных.Скачать

Понятие производной по направлению

Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению

Рассматривая функцию одной переменной, мы выяснили, что на оси Oy отображается приращение функции f(x) , соответствующее приращению аргумента x . Если мы имеем дело с функцией трёх переменных, то приращения аргументов x , y , z отображаются на осях Оx , Оy , Оz . Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?

И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.

Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, — это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).

Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:

1) функцию u = f(M) , определённую в окрестности точки M с координатами x , y , z ;

Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l . На получившейся прямой отметим точку M 1 , координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:

Величину отрезка MM 1 можно обозначить .

Функция u = f(M) при этом получит приращение

Определение производной по направлению. Предел отношения при , если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается , то есть

Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:

Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.

Видео:Частные производные функции многих переменныхСкачать

Примеры нахождения производной по направлению

Пример 1. Найти производную функции в точке M 0 (1; 2; 3) по направлению вектора .

Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:

Теперь можем найти производную по направлению данной функции по её формуле:

А сейчас — домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.

Пример 2. Найти производную функции в точке M 0 (1; 2) по направлению вектора , где M 1 — точка с координатами (3; 0) .

Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере — в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.

Пример 3. Найти производную функции в точке M 0 (1; 1; 1) по направлению вектора .

Решение. Найдём направляющие косинусы вектора

Найдём частные производные функции в точке M 0 :

Следовательно, можем найти производную по направлению данной функции по её формуле:

Видео:ЕГЭ 2017 Профильный №7 найти производную в точке касания #7Скачать

Градиент функции

Градиент функции нескольких переменных в точке M 0 характеризует направление максимального роста этой функции в точке M 0 и величину этого максимального роста.

Как найти градиент?

Нужно определить вектор, проекциями которого на оси координат являются значения частных производных , , этой функции в соответствующей точке:

То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.

Для градиента функции двух переменных формула короче: