Ав диаметр окружности точка к лежит на окружности (5 видео)

Задача 10469 Точка К лежит на диаметре АВ окружности.

Содержание

Условие
АВ — диаметр окружности. Точка С лежит на окружности. CD ⊥ АВ, AD = 3, DB = 5. Найдите CD.
Ваш ответ
решение вопроса
Похожие вопросы
Зачет №4 по теме «Окружность»
Зачет №4 по теме «Окружность»
📽️ Видео

Условие

Точка К лежит на диаметре АВ окружности с центром О. С и D — точки окружности, расположенные по одну сторону от АВ, причем угол OCK = углу ODK.

а) Докажите, что угол CKB = углу DKA.

б) Найдите площадь четырехугольника с вершинами в точках А, В, С, D, если известно, что OK = 3,6, BK = 9,6, угол OCK = углу ODK = 30°.

Видео:Окружность и круг, 6 классСкачать

АВ — диаметр окружности. Точка С лежит на окружности. CD ⊥ АВ, AD = 3, DB = 5. Найдите CD.

Видео:Радиус и диаметрСкачать

Ваш ответ

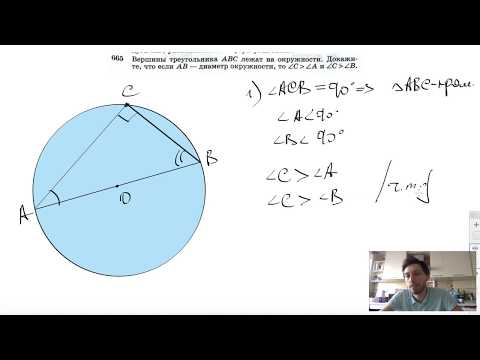
Видео:№665. Вершины треугольника ABC лежат на окружности. Докажите, что если АВ — диаметр окружностиСкачать

решение вопроса

Видео:№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать

Зачет №4 по теме «Окружность»

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Зачет №4 по теме «Окружность»

Проверка теоретических знаний.

У доски: доказать свойство касательной к окружности, теоремы о вписанном угле, об отрезках пересекающихся хорд, о серединном перпендикуляре к отрезку, об окружностях, вписанной в треугольник и описанной около треугольника.

Класс (фронтальная беседа).

Взаимное расположение прямой и окружности. Определение касательной к окружности и ее свойство. Какой угол называется центральным? Какой угол называется вписанным? Чему равна его градусная мера? Четыре замечательные точки треугольника. Какая окружность называется вписанной? Описанной? Какой многоугольник называется описанным? Вписанным? Каким свойством обладают стороны четырехугольника, описанного около окружности? Каким свойством обладают углы четырехугольника, вписанного в окружность? Сформулируйте теорему об отрезках пересекающихся хорд.

Т-1.Заполните пропуски (многоточия), чтобы получилось верное высказывание.

1. Точка, равноудаленная от всех точек окружности, называется ее. .

2. Отрезок, соединяющий две точки окружности, называется ее.

3. Все радиусы окружности.

4. На рисунке 0(r) — окружность, АВ — касательная к ней; точка В называется.

5. Прямая, имеющая с окружностью только одну общую точку, называется. к окружности.

6. Угол между касательной к окружности и радиусом, проведенным в точку касания, равен.

7. На рисунке АВ — диаметр окружности, С — точка, лежащая на окружности. Треугольник АСВ. (вид треугольника).

8. На рисунке АВ = 2ВС, АВ — диаметр окружности. Угол CAB равен.

9.На рисунке хорды АВ и CD пересекаются в точке М. Угол ACD равен углу.

10.На рисунке О — центр окружности. Дуга АmВ равна 120°. Угол АВС равен.

11.На рисунке АК = 24 см, KB = 9 см, CK = 12 см. Тогда KD = .

12*. На рисунке АВ = ВС = 13 см, высота BD = 12 см. Тогда ВК = . , КС = . .

1. Геометрическая фигура, все точки которой расположены на одинаковом расстоянии от заданной точки, называется.

2. Хорда, проходящая через центр окружности, называется.

3. Все диаметры окружности.

4. На рисунке 0(г) — окружность, В — точка касания прямой АВ и окружности. Прямая АВ называется. к окружности.

5. Прямая, имеющая с окружностью две общие точки, называется. окружности.

6. Касательная к окружности и радиус, проведенный в точку касания, .

7. На рисунке АВ — касательная, ОА — секущая, проходящая через центр окружности. Треугольник ОВА. (вид треугольника).

8. На рисунке ОС = СА, АВ — касательная к окружности с центром О. Угол ВАС равен.

9. Хорды АВ и CD окружности пересекаются в точке К. Угол ADC равен углу.

10. На рисунке О — центр окружности, угол СВА равен 40°. Дуга СmВ равна.

11. На рисунке AM = 15 см, MB = 4 см, MC = 3 см. Тогда DM = . .

12*. На рисунке АВ = ВС, BD — высота треугольника АВС, ВК = 8 см, КС = 5 см. Тогда BD= . DC = . .

Т-2.Установите, истинны или ложно следующие высказывания.

1. Прямая, имеющая с окружностью только одну общую точку, называется касательной к этой окружности.

2. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

3. На рисунке изображена окружность. Тогда Ð DAC = Ð DВС.

4. Всякая прямая, проходящая через середину хорды окружности, перпендикулярна к ней.

5. Луч касается окружности, если он имеет с ней только одну общую точку.

6. На рисунке АВ — диаметр окружности, Ð 1 = 30°. Тогда Ð 2 = 60°.

7. На рисунке изображена окружность. Тогда Ð DAB = Ð DOB.

8. На рисунке О — центр окружности. Если ÈВС = 60°, то Ð СВА = 60°.

9. На рисунке диаметр АВ окружности равен 10 см, хорда АС = 8 см. Тогда площадь треугольника АВС равна 24 см2.

10. Две хорды окружности АВ и CD пересекаются в точке О так, что АО = 16 см, ВО = 9 см, OD = 24 см. Тогда СО = 6 см.

11*. Точка касания окружности, вписанной в равнобедренный треугольник, делит боковую сторону на отрезки 5 см и 8 см, считая от основания. Тогда площадь треугольника равна 60 см2.

1. Прямая, расстояние до которой от центра окружности равно радиусу этой окружности, является касательной к ней.

2. Радиус, проведенный в точку касания прямой и окружности, перпендикулярен этой прямой.

3. На рисунке изображена окружность. Тогда Ð DAC = Ð DBC.

4. Прямая, перпендикулярная хорде окружности, делит эту хорду пополам.

5. Отрезок касается окружности, если он имеет с ней только одну общую точку.

6. На рисунке АВ — диаметр окружности. Тогда если Ð 2 = 50°, то Ð1 = 40°.

7. На рисунке изображена окружность. Тогда Ð АВС = ÐАОС.

8. На рисунке О — центр окружности. Тогда если ÐCAB — 60°, то È AC = 60°.

9. На рисунке диаметр BD окружности равен 13 см. Тогда если хорда ВС = 5 см, то площадь треугольника CBD равна 30 см2.

10. Две хорды окружности АВ и CD пересекаются в точке М так, что MB = 3 см, МА = 28 см, СМ = 21 см. Тогда MD = 4 см.

11*. Точка касания окружности, вписанной в равнобедренный треугольник, делит боковую сторону на отрезки 4 см и 6 см, считая от вершины. Тогда площадь этого треугольника равна 48 см2.

Т-3.В каждом задании установите верный ответ из числа предложенных.

1.На рисунке дуга АС равна 84°. Чему равен угол АВС, опирающийся на эту дугу?

А) 84°; Б) 42°; В) не знаю.

2. На рисунке угол МРК равен 88°. Чему равна дуга МК, на которую опирается угол МРК?

А) 88°; Б) 176°; В) не знаю.

3. Из точки А, находящейся на расстоянии двух радиусов от центра окружности, проведена касательная АВ. Чему равен угол ОАВ?

А) 60°; Б) 30°; В) не знаю.

4. Из точки М окружности проведены две хорды МА и MB. Хорда МА стягивает дугу, равную 80°, а угол АМВ равен 70°. Определите дугу, стягиваемую хордой MB.

А) 210°; Б) 140°; В) не знаю.

5. На рисунке диаметр АВ окружности равен 10 см, хорда ВС = 6 см. Найдите площадь треугольника АСВ.

А) 30 см2; Б) 24 см2; В) не знаю.

6. Из точки К окружности с центром О проведены две взаимно перпендикулярные хорды КМ и KD. Расстояние от точки О до хорды КМ равно 15 см, а до хорды KD равно 20 см. Каковы длины хорд КМ и KD7

A) 30 см и 40 см; Б) 15 см и 20 см; B) не знаю.

7. Две хорды АВ и CD точкой О их пересечения делятся так, что АО = 9 см, OB = 6 см, СО = 3 см. Какова длина отрезка OD7

А) 12 см; Б) 18 см; В) не знаю.

8. Из точки А к окружности проведены касательная АВ и секущая АС, проходящая через центр окружности. Расстояние от А до окружности равно 4 см, а диаметр окружности равен 12 см. Какова длина касательной?

А) 8 см; Б) 6 см; В) не знаю.

9*. Прямая АВ касается окружности с центром О и радиусом 5 см в точке А. Найдите расстояние от точки В до окружности, если длина касательной равна 12 см.

А) 7 см; Б) 8 см; В) не знаю.

1. На рисунке дуга АВ равна 164°. Чему равен угол АСВ, опирающийся на эту дугу?

А) 168°; Б) 82°; В) не знаю.

2. На рисунке угол АВС равен 44°. Чему равна дуга АС, на которую опирается угол АВС?

А) 88°; Б) 44°; В) не знаю.

3. Из точки М, находящейся на расстоянии двух радиусов от центра окружности, проведена касательная МК. Чему равен угол КОМ?

А) 60°; Б) 30°; В) не знаю.

4. Из точки А окружности проведены две хорды AM и АВ. Хорда AM стягивает дугу, равную 120°, а угол МАВ равен 80°. Определите величину дуги, стягиваемую хордой АВ.

А) 80°; Б) 120°; В) не знаю.

5. На рисунке диаметр АС окружности равен 13 см, хорда AB = 12 см. Найдите площадь треугольника АСВ.

А) 78 см2; Б) 30 см2; В) не знаю.

6. Из точки А окружности с центром О проведены две взаимно перпендикулярные хорды АВ и АС. Расстояние от точки О до хорды АВ равно 40 см, а до хорды АС равно 25 см. Каковы длины хорд АВ и АС?

A) 25 см и 40 см; Б) 50 см и 80 см; B) не знаю.

7. Две хорды МК и CD точкой Р их пересечения делятся так, что МР = 8 см, PC = 4 см. КР = 16 см. Какова длина отрезка PD.

А) 24 см; Б) 32 см; В) не знаю.

8. Из точки М к окружности проведены касательная МА и секущая МС, проходящая через центр окружности О. Расстояние от М до центра О равно 20 см, радиус окружности равен 12 см. Чему равна длина касательной?

А) 16 см; Б) 24 см; В) не знаю.

9*. Прямая АВ касается окружности с центром О и радиусом 5 см в точке В. Найдите длину касательной, если расстояние от точки А до окружности равно 8 см.

А) 13 см; Б) 12 см; В) не знаю.

Карточки для индивидуальной работы.

1. Сколько общих точек могут иметь прямая и окружность? Сформулируйте свойство и признак касательной.

2. Отрезок BD — высота равнобедренного треугольника AВС с основанием АС. На какие части окружность с центром В и радиусом BD делит боковую сторону треугольника если АВ= см, BD=5 см?

3. На рисунке изображен прямоугольный треугольник AВС, стороны которого касаются окружности радиуса 1 см. На какие отрезки точка касания делит гипотенузу треугольника, равную 5 см?

1. Какой угол называется вписанным? Сформулируйте теорему о вписанном угле.

2. Вершины треугольника со сторонами 2 см, 5 см и 6 см лежат на окружности. Докажите, что ни одна из сторон треугольника не является диаметром этой окружности.

3. На рисунке изображена окружность с центром О, АВ — касательная, а АС — секущая этой окружности. Найдите углы треугольника АВС, если ÈBD=62°.

1. Сформулируйте теорему об отрезках пересекающихся хорд.

2. Хорды KL и MN окружности пересекаются в точке А. Найдите АК и AL, если АМ=2 дм, AN=6 дм, KL=7 дм.

3. На рисунке изображена окружность с центром О, АС — диаметр, а ВС — касательная к этой окружности. На какие части отрезок АВ делится точкой D, если АС=20 см, ВС=15 см?

1. Сформулируйте теорему об окружности, вписанной в треугольник.

2. Впишите окружность в данный прямоугольный треугольник.

3. Основание равнобедренного треугольника равно 16 см, боковая сторона равна 17 см. Найдите радиус вписанной в этот треугольник окружности.

1. Сформулируйте утверждение о свойстве описанного четырехугольника. Верно ли обратное утверждение?

2. Найдите площадь прямоугольной трапеции, описанной около окружности, если боковые стороны этой трапеции равны 10 см и 16 см.

3. Площадь четырехугольника ABCD, описанного около окружности радиуса 5 дм, равна 90. Найдите стороны СD и AD этого четырехугольника, если AB=9 дм, ВС=10 дм.

1. Сформулируйте теорему об окружности, описанной около треугольника.

2. Постройте окружность, описанную около данного тупо угольного треугольника.

3. Найдите площадь равностороннего треугольника, вписанного в окружность радиуса 4 см.

1.Сформулируйте утверждение о свойстве вписанного четырехугольника. Верно ли обратное утверждение?

2. Площадь прямоугольника, вписанного в окружность, равна 48 см2. Найдите радиус окружности, если одна из сторон прямоугольника на 2 см больше другой.

3. На рисунке АМ и СМ — биссектрисы углов А и С треугольника АВС, AN и CN — биссектрисы внешних углов при вершинах A и С этого треугольника. Докажите, что около четырехугольника AMCN можно описать окружность.

По горизонтали: 1. Прямая, имеющая с окружностью две общие точки. 2. Отображение плоскости на себя. 3. Удвоенный радиус.

По вертикали: 4. Единица измерения угла или 1/60 минуты. 5. Часть круга, ограниченная двумя радиусами и дугой окружности круга. 6. Отрезок, соединяющий центр окружности с любой точкой окружности. 7. Определение точки окружности.

Примечание: в разработке использованы материалы из газеты «Математика».