Дан тетраэдр dabc плоскость альфа проходит через прямую cd и параллельна прямой ав

Видео:10 класс, 12 урок, ТетраэдрСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Построение сечений тетраэдра

Содержание: Актуализация; Изучение нового; Закрепление; Разноуровневая проверочная самостоятельная работа ( 4 варианта) с разбором решения;

* А1 Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.

* А2 Если две точки прямой лежат в плоскости, то и вся прямая лежит в этой плоскости.

* А3 Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. В любой плоскости выполняются аксиомы планиметрии.

АКСИОМЫ СТЕРЕОМЕТРИИ . 1. Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость. 2. Если две точки прямой лежат в плоскости, то и вся прямая лежит в этой плоскости. 3. Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. В любой плоскости выполняются аксиомы планиметрии.

* ОПРЕДЕЛЕНИЯ 1. Две прямые, имеющие только одну общую точку, называются пересекающимися. 2. Две прямые, лежащие в одной плоскости и не имеющие общих точек, называются параллельными. 3 Две прямые, не лежащие в одной плоскости, называются скрещивающимися. 4. Прямая, все точки которой принадлежат плоскости, называется прямой, лежащей в этой плоскости.

* ОПРЕДЕЛЕНИЯ (ПРОДОЛЖЕНИЕ) 5. Прямая пересекает плоскость, если у них есть только одна общая точка. 6. Прямая называется параллельной плоскости, а плоскость- параллельной прямой, если они не имеют общих точек. 7. Прямая называется перпендикулярной плоскости (а плоскость прямой), если прямая перпендикулярна любой прямой, лежащей в этой плоскости.

* ТЕОРЕМЫ 1. Через прямую и не лежащую на ней точку проходит одна и только одна плоскость. 2. Через две пересекающиеся прямые проходит одна и только одна плоскость. 3. Через две параллельные прямые проходит одна и только одна плоскость. 4. Если одна из параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.

Построение сечения тетраэдра через точки M, N, K А B D C N M K

Построение сечения тетраэдра через точки M, N, K А B D C N M K F

Построение сечения тетраэдра через точки M, N, K А B D C N M K L F

Построение сечения тетраэдра через точки M, N, K А B D C N M K L F

А B D C N M K Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а.

А B D C N M K Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а.

А B D C N M K Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а. E

А B D C N M K Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K MN ║ AC E

А B D C N M Е Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K K Р

А B D C N M Е Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K K Р

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C N M Q Построите сечение тетраэдра DABC плоскостью, проходящей через возможные точки K Р R

А B D C L M Q Построите сечение тетраэдра DABC плоскостью, проходящей через возможные точки K Р R

А B D C N M Построите сечение тетраэдра DABC плоскостью, проходящей через возможные точки

Самостоятельная работа Вариант 1 Вариант 2 Вариант 3 Вариант 4 Задание 1 Задание 2 Задание 3 Задание 1 Задание 2 Задание 3 Задание 1 Задание 2 Задание 3 Задание 1 Задание 2 Задание 3

Вариант 1 Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MNK. ответ

Вариант 1 ответ Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MNK. B N Х

Вариант 1 Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; С Є MND. А B С ответ

Вариант 1 ответ Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; С Є MND. А B С

Вариант 1 Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B М С ответ

Вариант 1 ответ Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B М С

Вариант 2 Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MDK. А B ответ

Вариант 2 ответ Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MDK. А B Х

Вариант 2 Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; В Є NDK. А B C ответ

Вариант 2 ответ Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; В Є NDK. А B C

Вариант 2 Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B С ответ

Вариант 2 ответ Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B N С

Вариант 3 Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MND. А B ответ

Вариант 3 ответ Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MND. А B N Х

Вариант 3 Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; В Є NDK. C B А ответ

Вариант 3 ответ Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; В Є NDK. C B А

Вариант 3 Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B С ответ

Вариант 3 ответ Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B К С

Вариант 4 Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MDK. А B ответ

Вариант 4 ответ Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MDK. А B Х

Вариант 4 Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; С Є MDN. А B C ответ

Вариант 4 ответ Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; С Є MDN. А B C

Вариант 4 Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А С В ответ

Вариант 4 ответ Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А С N В

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 342 человека из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 689 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Усенко Ольга АлександровнаНаписать 5165 04.02.2016

Номер материала: ДВ-415338

04.02.2016 277

04.02.2016 1054

04.02.2016 352

04.02.2016 837

04.02.2016 2924

04.02.2016 1053

04.02.2016 590

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

В России разработают рекомендации по сопровождению студентов с ОВЗ

Время чтения: 2 минуты

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

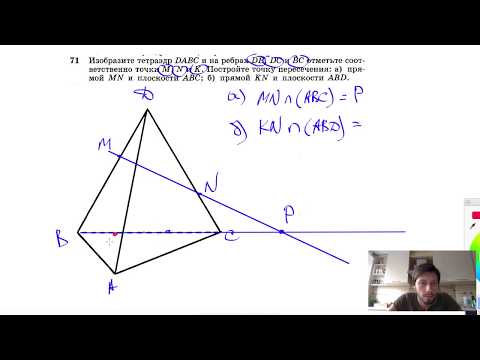
Видео:№71. Изобразите тетраэдр DABC и на ребрах DB, DC и ВС отметьте соответственно точки М, N и К.Скачать

Через точку K на ребре АD тетраэдра DABC проведено сечение параллельно грани равна АВС площадь сечения равна 27, АК : КД = 1 : 3?

Геометрия | 10 — 11 классы

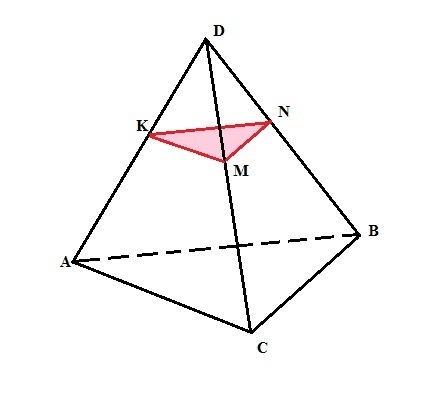
Через точку K на ребре АD тетраэдра DABC проведено сечение параллельно грани равна АВС площадь сечения равна 27, АК : КД = 1 : 3.

НАЙДИТЕ ПЛОЩАДЬ ГРАНИ АВС.

Пусть проведенное сечение пересекает ребра тетраэдра DC и DB в точках M и N соответственно.

Значит сечение представляет собой треугольник KMN, параллельный треугольнику АВС и подобен ему в силу параллельности их соответственных сторон.

Рассмотрим треугольники DKM и DAC.

Они подобны, так как КМ║АС.

AK = x, тогда KD = 3х.

Это коэффициент подобия треугольников.

Итак, КМ / АС = 3 / 4.

= &gt ; это коэффициент подобия треугольников KMN и АВС.

Площади подобных фигур относятся как квадрат коэффициента подобия этих фигур, то есть Skmn / Sabc = (3 / 4)² и Sabc = 16 * Skmn / 9 = 16 * 27 / 9 = 48 ед².

Ответ : Sabc = 48 ед².

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

ОЧЕНЬ СРОЧНО НАДО?

ОЧЕНЬ СРОЧНО НАДО!

Ребро правильного тетраэдра dabc равно а постройте сечение тетраэдра проходящего через середину ребра DA параллельно плоскости DBC.

Найти площадь построенного сечения.

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

СРОЧНО НАДО?

Ребро правильного тетраэдра dabc равно а постройте сечение тетраэдра проходящего через середину ребра DA параллельно плоскости DBC.

Найти площадь построенного сечения.

Видео:Как строить сечения тетраэдра и пирамидыСкачать

Площадь сечения правильного тетраэдра DABC, проходящего через ребро AC и середину ребра DB, равна 9 корень 2 см в квадрате?

Площадь сечения правильного тетраэдра DABC, проходящего через ребро AC и середину ребра DB, равна 9 корень 2 см в квадрате.

Найдите площадь полной поверхности тетраэдра.

Видео:№72. Изобразите тетраэдр DABC и постройте сечение этого тетраэдра плоскостью, проходящейСкачать

В тетраэдре DABC точка F лежит на ребре BC?

В тетраэдре DABC точка F лежит на ребре BC.

Постройте сечение этого тетраэдра, проходящее через точку А параллельно прямым AB и CD.

Определите вид построенного сечения.

Видео:№173. Ребро CD тетраэдра ABCD перпендикулярно к плоскости ABC, АВ = ВС = АС = 6Скачать

Пожалуйста помогите, очень надо1) Изобразите тетраэдр ABCD и отметьте точку М на ребре АВ?

Пожалуйста помогите, очень надо

1) Изобразите тетраэдр ABCD и отметьте точку М на ребре АВ.

Постройте сечение тетраэдра с плоскостью , проходящей через точку М параллельно прямым АС и BD.

2)Изобразите тетраэдр DABC, отметьте точку К на ребре DC и точки M и N граней АВС и ACD.

Постройте сечение тетраэдра плоскостью MNK.

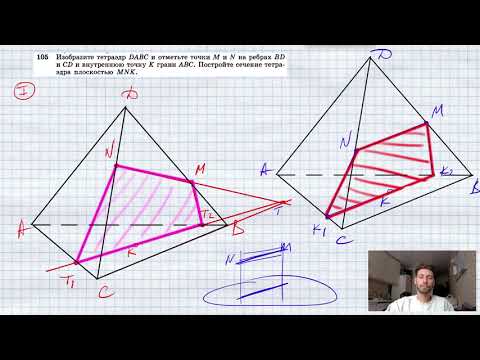
Видео:№105. Изобразите тетраэдр DABС и отметьте точки М и N на ребрах BD и CD и внутреннюю точку К грани AСкачать

Ребро правильного тетраэдра DABC равно 2см?

Ребро правильного тетраэдра DABC равно 2см.

Постройте сечение тетраэдра, проходящее через середину ребра DA параллельно плоскости DBC , и найдите площадь этого сечение.

Видео:Как строить сечения параллелепипедаСкачать

Через точку пересечения медиан грани BCD тетраэдра проведена плоскость , параллельна грани ABC?

Через точку пересечения медиан грани BCD тетраэдра проведена плоскость , параллельна грани ABC.

Площадь полученного сечения равна 48 см ^ 2.

Найдите площадь грани АВС.

Видео:Тетраэдр. 10 класс.Скачать

В кубе АВСДА1В1С1Д1 проведено сечение через вершину А середину ребра ВС и центр грани ДСС1Д1?

В кубе АВСДА1В1С1Д1 проведено сечение через вершину А середину ребра ВС и центр грани ДСС1Д1.

Вычислите площадь сечения если сторона куба равна а.

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Точка К делит ребро РА правильного тетраэдра РАВ в отношении РК : КА = 2 : 3?

Точка К делит ребро РА правильного тетраэдра РАВ в отношении РК : КА = 2 : 3.

Постройте сечение тетраэдра плоскостью параллельной плоскости (АВС) и проходит через К.

Найти площадь сечения, если АВ = 10см.

Видео:ПОСТРОЕНИЕ СЕЧЕНИЙ ТЕТРАЭДРА ПЛОСКОСТЬЮСкачать

Через точку К на ребре CD тетраэдра DABC проведено сечение параллельно грани ABC?

Через точку К на ребре CD тетраэдра DABC проведено сечение параллельно грани ABC.

Площадь сечения равна 48, CK : KD = 1 : 4.

Найдите площадь сечения.

Вопрос Через точку K на ребре АD тетраэдра DABC проведено сечение параллельно грани равна АВС площадь сечения равна 27, АК : КД = 1 : 3?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 10 — 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Ответ : |Am = √13 ед. |АС| = 5 ед. Объяснение : Вектор Am равен сумме векторов АВ и Вm. Вектор AС равен сумме векторов АВ и ВС. Модуль суммы двух векторов можно вычислить, используя теорему косинусов : |Аm|² = |AB|² + |Bm|² + 2 * |AB| * |Bm| * Co..

4х + х + х = 180 градусов х = 30 градусов углы : 30 30 и 120 медиана = боковая сторона синуса синус а = 30 градусов — а это 0. 5 6 = х * 0. 5 х = 12 ответ : 12см.

Свойство вн. Угла это сумма двух углов ∆ не смежные с ним. Поэтому 47 + 72 = 119.

Угол АОВ = 180 — 100 = 80 градусов(смежные угла) 2) АО = ВО(радиусы равны) 3)треугол. АОВ равнобедренный следовательно, Угол Ова и угол ОАВ = 180 — 80 = 100 : 2 = 50 градусов(по св. Равнобедренных треугольников.

1. BD = AC OB = OC BD = BO + OB AC = OC + AO Тогда AO = OB. Итак, BO = BO, AO = OB, ∠BOA = ∠COA — как вертикальные, значит, ΔAOB = ΔCOD — по I признаку. 2. ∠BOA = 180° — ∠1 — как смежные ∠BOC = 180° — ∠2 — как смежные Но∠1 = ∠2⇒∠BOA = ∠BOC. Итак, ..

Ρ = m / V V = 4 / 3 * π R³ = 4 / 3 * π * 0, 3³≈ 4 / 3 * 3 * 0, 027 = 0, 908(м³) ρ = 118, 75 / 0, 908 ≈ 130, 8кг / м³.

Дано : SАВС — правильная пирамида, ΔАВС — правильный, АВ = ВС = АС = 6 см ; SО — высота пирамиды равна 12 см. Построим ВК⊥АС, ВК — высота, медиана и биссектрисаΔАВС. ОК : ОВ = 1 : 2. ΔВСК. СК = 0, 5·АС = 3 см. ВК² = ВС² — СК² = 36 — 9 = 27, ВК =..

2АК = КС, значит АК : КС = 1 : 2 и АК : АС = 1 : 3. Следствием теоремы о площади треугольника по его стороне и высоте, к ней проведённой, является то, что отношение площадей треугольников с одинаковыми высотами равно отношению их сторон, к которым в..

Поскольку в трапеции основы паралельные, то имеем равнобедренный треугольник с основой диагональю. Получаем что боки равнобокой трапеции равны по 12. Отсуда периметр 12 + 12 + 12 + 18 = 36 + 18 = 54.

Видео:№104. Изобразите тетраэдр ABCD и отметьте точку М на ребре АВ. Постройте сечение тетраэдра плоскостьСкачать

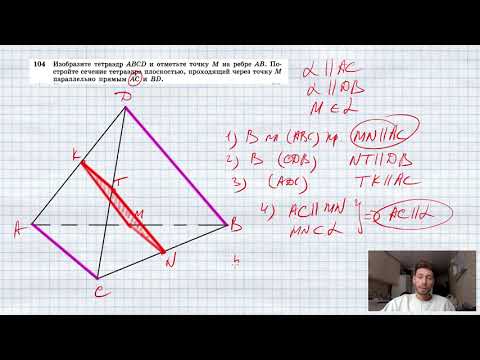
Построение сечений тетраэдра. 10-й класс

Разделы: Математика

Класс: 10

Цели урока: (Приложение 1, слайды 1-2)

• научиться применять аксиомы стереометрии при решении задач;
• научиться находить положение точек пересечения секущей плоскости с рёбрами тетраэдра;
• освоить методы построения этих сечений
• формировать познавательную активность, умения логически мыслить;
• создать условия самоконтроля усвоения знаний и умений.

Тип урока: Формирование новых знаний.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Ход урока

I. Организационный момент

II. Актуализация знаний учащихся

Фронтальный опрос. (Аксиомы стереометрии, свойства параллельных плоскостей)

Слово учителя

Для решения многих геометрических задач, связанных с тетраэдром, полезно уметь строить на рисунке их сечения различными плоскостями. (слайд 3) . Назовём секущей плоскостью тетраэдра любую плоскость, по обе стороны от которой имеются точки данного тетраэдра. Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра. Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники. Отметим также, что для построения сечения достаточно построить точки пересечения секущей плоскости с рёбрами тетраэдра, после чего остаётся провести отрезки, соединяющие каждые две построенные точки, лежащие в одной и той же грани.

На этом уроке вы сможете подробно изучить сечения тетраэдра, освоить методы построения этих сечений. Вы узнаете пять правил построения сечений многогранников, научитесь находить положение точек пересечения секущей плоскости с рёбрами тетраэдра.

Актуализация опорных понятий

• Первое правило. Если две точки принадлежат как секущей плоскости, так и плоскости некоторой грани многогранника, то прямая, проходящая через эти две точки, является линией пересечения секущей плоскости с плоскостью этой грани (следствие аксиомы о пересечении плоскостей).
• Второе правило. Если секущая плоскость параллельна некоторой плоскости, то эти две плоскости пересекаются с любой гранью по параллельным прямым (свойство двух параллельных плоскостей, пересечённых третьей).
• Третье правило. Если секущая плоскость параллельна прямой, лежащей в некоторой плоскости (например, плоскости какой-то грани), то линия пересечения секущей плоскости с этой плоскостью (гранью) параллельна этой прямой (свойство прямой, параллельной плоскости).
• Четвёртое правило. Секущая плоскость пересекает параллельные грани по параллельным прямым (свойство параллельных плоскостей, пересечённых третьей).
• Пятое правило. Пусть две точки А и В принадлежат секущей плоскости, а точки A₁ и B₁ являются параллельными проекциями этих точек на некоторую грань. Если прямые АВ и A₁B₁ параллельны, то секущая плоскость пересекает эту грань по прямой, параллельной A₁B₁. Если же прямые АВ и A₁B₁ пересекаются в некоторой точке, то эта точка принадлежит как секущей плоскости, так и плоскости этой грани (первая часть этой теоремы следует из свойства прямой, параллельной плоскости, а вторая вытекает из дополнительных свойств параллельной проекции).

III. Изучение нового материала (формирование знаний, умений)

Коллективное решение задач с объяснением (слайд 4)

Задача 1. Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки К є АД, М є ДС, Е є ВС.

Внимательно посмотрим на чертёж. Так как точки К и М принадлежат одной плоскости, то мы находим пересечение секущей плоскости с гранью АДС – это отрезок КМ. Точки М и Е также лежат в одной плоскости, значит пересечением секущей плоскости, и грани ВДС является отрезок МЕ. Находим точку пересечения прямых КМ и АС, которые лежат в одной плоскости АДС. Теперь точка Х лежит в грани АВС, то её можно соединить с точкой Е. Проводим прямую ХЕ, которая пересекается с АВ в точке Р. Отрезок РЕ есть пересечение секущей плоскости с гранью АВС, а отрезок КР есть пересечение секущей плоскости с гранью АВС. Следовательно, четырёхугольник КМЕР наше искомое сечение. Запись решения в тетради:

1. КМ = α ∩ АДС
2. МЕ = α ∩ ВДС
3. Х = КМ ∩ АС
4. Р = ХЕ ∩ АВ
5. РЕ = α ∩ АВС
6. КР = α ∩ АДВ
7. КМЕР – искомое сечение

Задача 2. (слайд 5)

Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки К є АВС, М є ВДС, N є АД

Проанализируем этот рисунок. Здесь нет точек, лежащих в одной грани. В это случае воспользуемся правилом 5. Рассмотрим проекции каких-нибудь двух точек. В тетраэдре проекции точек находят из вершины на плоскость основания, т.е. М→М₁, N→А. Находим пересечение прямых NM и AM₁ точку Х.Данная точка принадлежит секущей плоскости, так как лежит на прямой NM, принадлежит плоскости АВС, так как лежит на прямой АМ₁. Значит, теперь в плоскости АВС у нас есть две точки, которые можно соединить, получаем прямую КХ. Прямая пересекает сторону ВС в точке L, а сторону АВ в точке Н. В грани АВC находим линию пересечения, она проходит через точки Н и К – это НL. В грани АВД линия пересечения – НN, в грани ВДС проводим линию пересечения через точки L и М – это LQ и в грани АДС получаем отрезок NQ. Четырёхугольник HNQL – искомое сечение.

1. М → М₁ N → А
2. Х = NМ ∩ АМ₁
3. L = КХ ∩ ВС
4. H = КХ ∩ АВ
5. НL = α ∩ АВC, К є НL
6. НN = α ∩ АВД,
7. LQ = α ∩ ВДС, М є LQ
8. NQ = α ∩ АДС
9. HNQL – искомое сечение

IV. Закрепление знаний

Работа с анимационным объектом «Построение сечения тетраэдра с плоскостью» (диск «Уроки геометрии в 10 классе» урок №16)

Решение задачи с последующей проверкой

Задача 3. (слайд 6)

Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки К є ВС , М є АДВ, N є ВДС.

1. 1. М → М₁ , N → N₁
2. Х = NМ ∩ N₁М₁
3. R = КХ ∩ АВ
4. RL = α ∩ АВД, М є RL
5. КР = α ∩ ВДС, N є КР
6. LP = α ∩ АДС
7. RLPK – искомое сечение

V. Самостоятельная работа (по вариантам)

Задача 4. Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки М є АВ, N є АС, К є АД.

1. КМ = α ∩ АВД,
2. МN = α ∩ АВС,
3. КN = α ∩ АДС
4. KMN – искомое сечение

(Проверка по гиперссылке на Приложение 2)

Задача 5. Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки М є АВ, К є ДС, N є ДВ.

1. MN = α ∩ АВД
2. NK = α ∩ ВДС
3. Х = NК ∩ ВС
4. Р = АС ∩ МХ
5. РК = α ∩ АДС
6. MNKP – искомое сечение

Задача 6. Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки М є АВС, К є ВД, N є ДС

1. KN = α ∩ ДВС
2. Х = КN ∩ ВС
3. Т = МХ ∩ АВР = ТХ ∩ АС
4. РТ = α ∩ АВС, М є РТ
5. PN = α ∩ АДС
6. ТР N K – искомое сечение

VI. Итог урока.

Итак, мы сегодня научились строить простейшие задачи на сечения тетраэдра. Напоминаю, что сечением многогранника называется многоугольник, полученный в результате пересечения многогранника с некоторой плоскостью. Сама плоскость при этом называется секущей плоскостью. Построить сечение значит определить, какие рёбра пересекает секущая плоскость, вид полученного сечения и точное положение точек пересечения секущей плоскости с этими рёбрами. То есть, те цели, которые были поставлены на уроке, решены.

VII. Домашнее задание.

Практическая работа «Построить сечения тетраэдра» в электронном виде или бумажном варианте. (Каждому было дано индивидуальное задание).

🎥 Видео

№69. Через середины ребер АВ и ВС тетраэдра SABC проведена плоскость параллельно ребру SBСкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

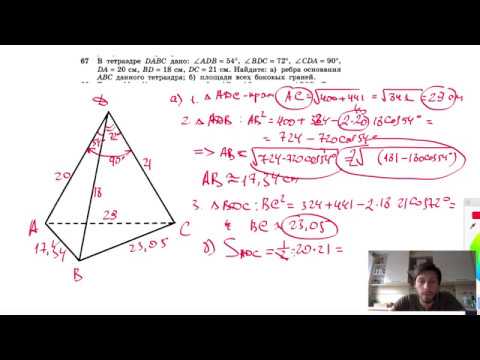
№67. В тетраэдре DABC дано: ∠ADB = 54°, ∠BDC = 72°, ∠CDA =90°, DA=20 см,Скачать

10 класс, 10 урок, Параллельные плоскостиСкачать

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать