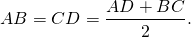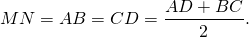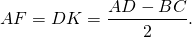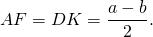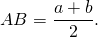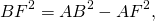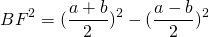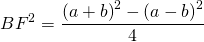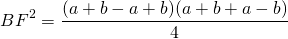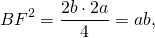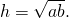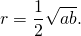Укажите номера верных утверждений.
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «В любую равнобедренную трапецию можно вписать окружность.» — неверно, не в любую равнобедренную трапецию можно вписать окружность.
2) «Диагональ параллелограмма делит его углы пополам.» — неверно, диагональ параллелограмма делит его углы пополам только в том случае, когда параллелограмм является ромбом.
3) «Площадь прямоугольного треугольника равна половине произведения его катетов.» — верно, это теорема планиметрии.
Аналоги к заданию № 311763: 311915 311959 Все
Видео:Задача про трапецию, описанную около окружностиСкачать
Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Видео:В равнобедренную трапецию Р=40, S=80 можно вписать окружность. Найдите расстояние от точки пересеченСкачать
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники 
и 
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия – 
Отношение площадей этих треугольников есть 
.
4. Треугольники 
и 
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Видео:В равнобедренную трапецию, периметр которой равен 180, а площадьравна 1620, можно вписать...Скачать
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать
Вписанная окружность
Если в трапецию вписана окружность с радиусом 
и она делит боковую сторону точкой касания на два отрезка — 
и 
, то 
Видео:Окружность, вписанная в трапециюСкачать
Площадь
или 
где 
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Видео:Кто нибудь знает при каких условиях в трапецию можно вписать окружность Как описать тест УчителюСкачать
Вписанная в равнобедренную трапецию окружность
Какими свойствами обладает вписанная в равнобедренную трапецию окружность?
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.
Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
Если MN —
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.
По свойству равнобедренной трапеции,
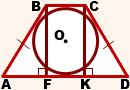
Из прямоугольного треугольника ABF по теореме Пифагора
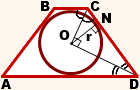
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,
🔍 Видео
№700. Докажите, что в любой ромб можно вписать окружность.Скачать
Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать
Все виды №25 из банка ФИПИ ОГЭ по математикеСкачать
Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать
8 класс, 6 урок, ТрапецияСкачать
ОГЭ/База Все прототипы задач на окружностиСкачать
Решаем планиметрию 16 задание подряд | ЕГЭ математика 2023Скачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Разбор задания 13 ОГЭ по математикеСкачать
Если в четырёхугольник можно вписать окружностьСкачать
Четырёхугольники №17 из ОГЭ. Биссектриса и прямоугольные треугольники в четырёхугольниках.Скачать
8 класс, 38 урок, Вписанная окружностьСкачать
Окружность в задании №6 ЕГЭ по математикеСкачать
Слили планиметрию из ЕГЭ 2024 по математике | 3-х часовой стрим | №17 на счет | Веб будет удаленСкачать
