Дан параллелограмм oabc векторы oa

Презентация к уроку введения нового материала.

Просмотр содержимого документа
«Координаты вектора. Правила нахождения координат суммы, разности векторов, произведения вектора на число.»

Урок по геометрии в 9 классе

Учитель Гуськова Е.Е,

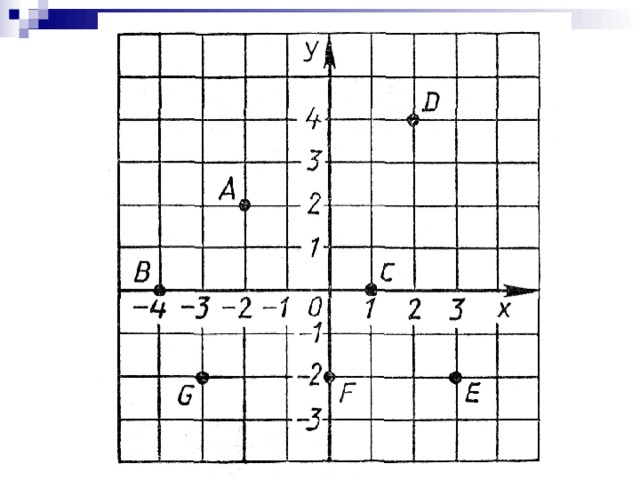
Найдите абсолютную величину вектора:

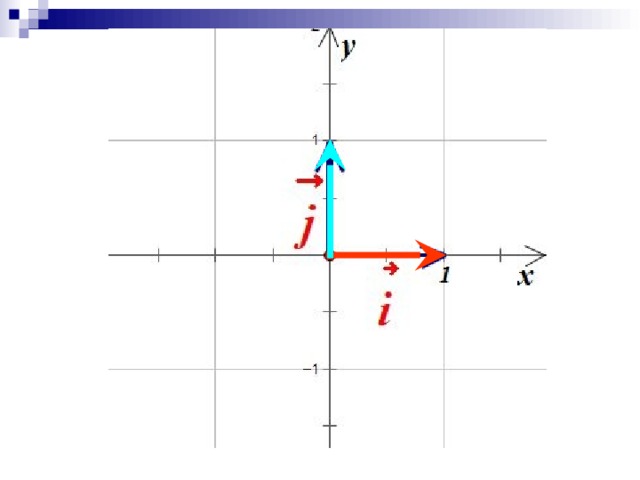
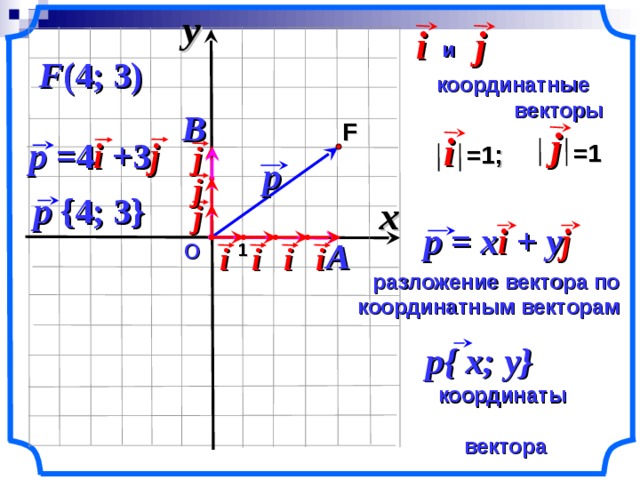
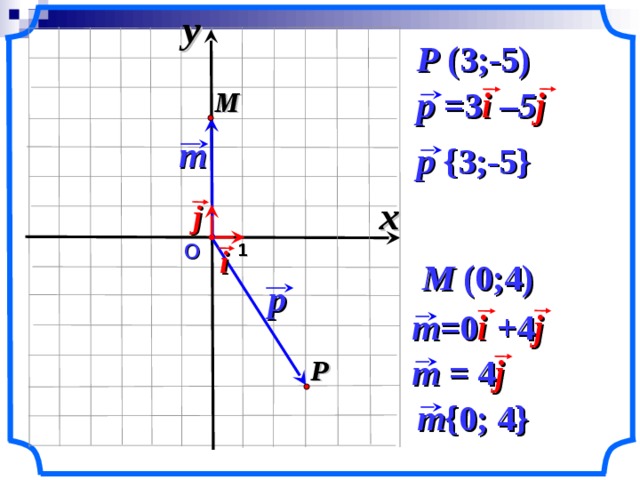
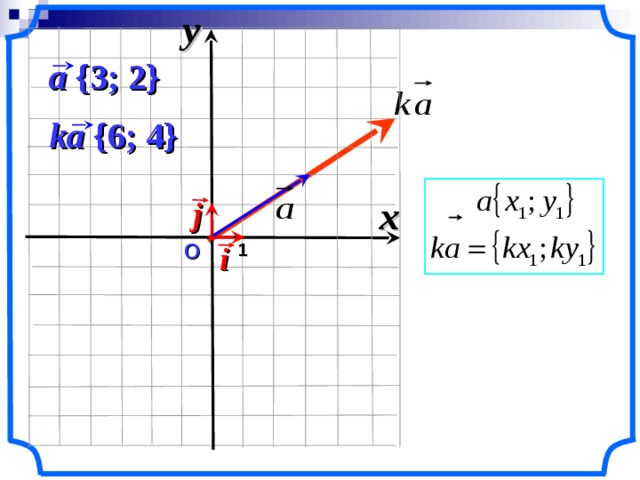
разложение вектора по координатным векторам

«Геометрия 7-9» Л.С. Атанасян и др.

«Геометрия 7-9» Л.С. Атанасян и др.

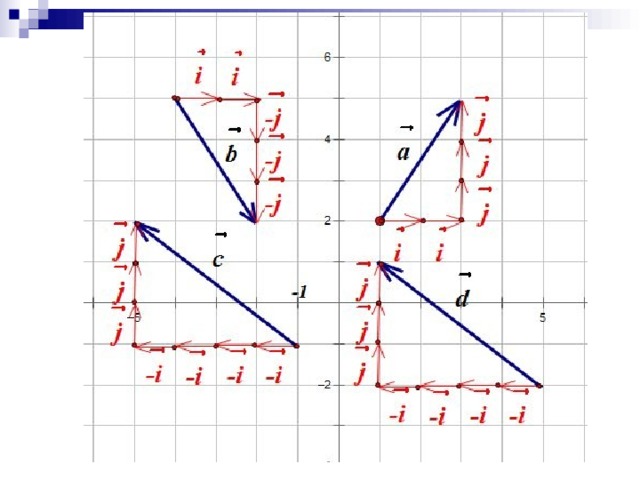
Разложение вектора по координатным векторам

«Геометрия 7-9» Л.С. Атанасян и др.

«Геометрия 7-9» Л.С. Атанасян и др.

«Геометрия 7-9» Л.С. Атанасян и др.

«Геометрия 7-9» Л.С. Атанасян и др.

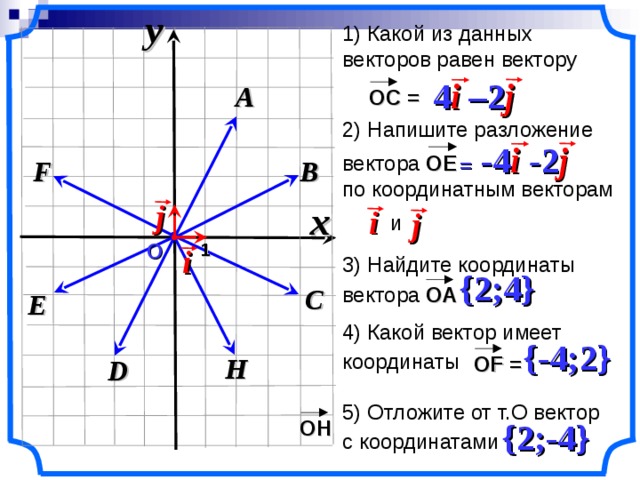
1) Какой из данных векторов равен вектору

2 ) Напишите разложение

по координатным векторам

3 ) Найдите координаты

Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)

4 ) Какой вектор имеет

5 ) Отложите от т.О вектор

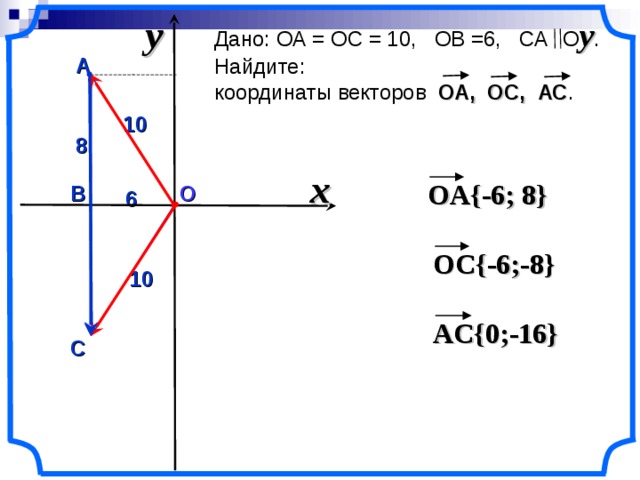
Дано: ОА = ОС = 10, ОВ =6, СА О y . Найдите :

координаты векторов ОА, ОС, АС .

Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)

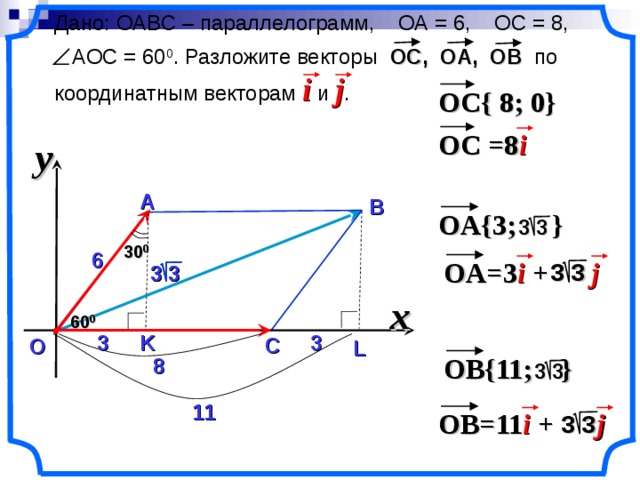
Дано: OABC – параллелограмм, ОА = 6, ОС = 8,

АОС = 60 0 . Разложите векторы О C , О A , ОВ по координатным векторам i и j .

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Математический портал

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Nav view search

Navigation

Search

• Вы здесь:
• Home

Видео:№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать

Базис линейного пространства. Разложение вектора по базису.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Упорядоченная тройка некомпланарных векторов $e_1, e_2, e_3$ называется базисом в пространстве всех геометрических векторов. Всякий геометрический вектор $a$ может быть представлен единственным образом в виде $$a=X_1e_1+X_2e_2+X_3e_3.qquadqquadqquadqquadqquad (1)$$ Числа $X_1, X_2, X_3$ называются координатами вектора в базисе $B=.$ Запись (1) называют разложением вектора $a$ по базису $B.$

Аналогично, упорядоченная пара неколлинеарных векторов $e_1, e_2$ называется базисом $B=(e_1, e_2)$ в множестве геометрических векторов, компланарных некоторой плоскости.

Наконец, всякий ненулевой вектор $e$ образует базис $B=(e)$ в множестве геометрических векторов, коллинеарных некоторому направлению.

Если вектор $a$ есть линейная комбинация векторов $a_1, a_2, . a_n$ с коэффициентами $lambda_1, lambda_2, . lambda_n$, то есть $$a=sumlimits_^n lambda_ka_k$$ то каждая координата $X_i(a)$ вектора $a$ равна сумме произведений коэффициентов $lambda_1,lambda_2. lambda_n$ на одноименные координаты векторов $a_1, a_2, . a_n: $ $$X_i(a)=sumlimits_^nlambda_k X_i(a_k),qquad (i=1, 2, 3.)$$

Базис $B=(e_1, e_2, e_3)$ называется прямоугольным, если векторы $e_1, e_2$ и $e_3$ попрано перпендикулярны и имеют единичную длину. В этом случае приняты обозначения $$e_1=i;,, e_2-j;,, e_3=k.$$

Примеры.

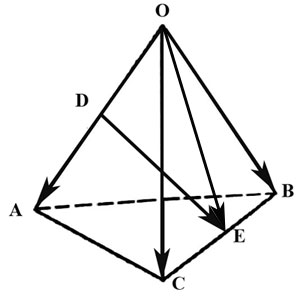
2.26. Задан тетраэдр $OABC.$ В базисе из ребер $overline, overline$ и $overline$ найти координаты:

а) вектора $overline,$ где $D$ и $E$ середины ребер $OA$ и $BC.$

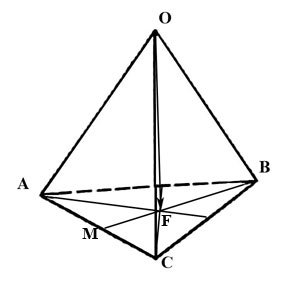
б) вектора $overline,$ где $F-$ точка пересечения медиан основания $ABC.$

Решение.

а)

Выразим вектор $overline$ через вектора $overline, overline, overline:$

Из треугольника $ODE$ имеем $overline=overline+overline.qquadqquadqquad (1)$

вектор $overline$ найдем из треугольника $OBE:$

здесь $overline=fracoverline,$ а вектор $overline$ находим из треугольника $OBC:$

Таким образом, из (2) получаем $overline=overline+frac(overline-overline).$

Наконец из (1) имеем $$overline=overline+overline=-fracoverline+overline+frac(overline-overline)=$$ $$=-fracoverline+fracoverline+fracoverline.$$

Таким образом, координаты вектора $overline$ в базисе из ребер $overline, overline, overline:$ $left(-frac,frac,fracright).$

Ответ: $left(-frac; frac; fracright).$

б)

Выразим вектор $overline$ через вектора $overline, overline, overline:$

Из треугольника $OFB$ имеем $overline=overline+overline.qquadqquadqquad (1)$

вектор $overline$ найдем из треугольника $BMC:$

здесь $overline=fracoverline,$ а вектор $overline$ находим из треугольника $OCA:$

Таким образом, из (2) получаем $$overline=overline+overline=overline-overline+fracoverline=$$ $$=overline-overline+frac(-overline+overline).$$

Наконец из (1) имеем $$overline=overline+overline=overline+fracoverline=$$ $$=overline+fracleft(overline-overline+frac(-overline+overline)right)=$$ $$=overline+fracoverline-fracoverline+frac(-overline+overline)=fracoverline+fracoverline+fracoverline.$$

Таким образом, координаты вектора $overline$ в базисе из ребер $overline, overline, overline:$ $left(frac; frac; fracright).$

Ответ: $left(frac; frac; fracright).$

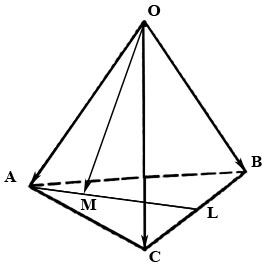
2.27. В тетраэдре $OABC$ медиана $AL$ грани $ABC$ делится точкой $M$ в отношении $|overline|:|overline|=3:7.$ Найти координаты вектора $overline$ в базисе из ребер $overline, overline, overline.$

Решение.

Вектор $overline$ найдем из треугольника $AOM:$ $$overline=overline+overline.qquadqquadqquad (1)$$

Из условия $|overline|:|overline|=3:7$ имеем $overline=fracoverline.$ Из треугольника $ABL$ находим $overline=overline+overline=overline+fracoverline.$

Далее, из треугольников $AOB$ и $BOC$ получаем

Отсюда и из (1) получаем $$overline=overline+overline=overline+fracoverline+fracoverline+fracoverline=$$ $$=fracoverline-fracoverline+fracoverline.$$

Ответ: $left(frac; frac;fracright).$

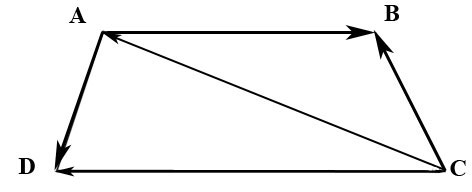
2.29. В трапеции $ABCD$ известно отношение длин оснований $|overline|/|overline|=lambda$ Найти координаты вектора $overline$ в базисе из векторов $overline$ и $overline.$

Решение.

Вектор $overline$ можно найти из треугольника $ABC:$ $overline=overline+overline.$

$overline$ находим из треугольника $ACD:$ $overline=overline+overline=overline-overline.$

Из условия $|overline|/|overline|=lambda$ находим вектор $overline:$ $overline=-overline/lambda.$

Таким образом, $overline=-overline/lambda-overline;$

2.36. Заданы векторы $e(-1, 1, 1/2)$ и $a(2, -2, -1).$ Убедиться, что они коллинеарны и найти разложение вектора $a$ по базису $B(e). $

Решение.

Векторы коллинеарны, если их направления совпадают или противоположны, т.е. тогда и только тогда когда их координаты пропорциональны. Проверим: $$frac=frac=frac=-frac,$$ то есть векторы $e$ и $a$ коллинеарны.

Найдем разложение вектора $a$ по базису $B(e),$ то есть найдем такое число $lambda$ что $a=lambda e:$

Ответ: $a=-2e.$

Домашнее задание.

2.28. Вне плоскости параллелограмма $ABCD$ взята точка $O.$ В базисе из векторов $overline, overline$ и $overline$ найти координаты:

а) вектора $overline$ , где $M$ точка пересечения диагоналей параллелограмма;

б) вектора $overline,$ где $K$- середина стороны $AD.$

Ответ: а) $(1/2; 0; 1/2);$ б) $(1, -1/2, 1/2).$

2.31. В треугольнике $ABC$ $overline=alphaoverline; overline=betaoverline;$ $overline=gammaoverline.$ Пусть $P, Q$ и $R -$ точки пересечения прямых $BF$ и $CK;$ $CK$ и $AM;$ $AM$ и $BF$ соответственно. В базисе из векторов $overline$ и $overline$ найти координаты векторов $overline,$ $overline$ и $overline.$

2.37. На плоскости заданы векторы $e_1(-1,2),$ $e_2(2,1)$ и $a(0,-2).$ Убедиться, что базис $B=e_1, e_2$ в множестве всех векторов на плоскости Построить заданные веткоры и найти разложение вектора $a$ по базису $B.$

Ответ: $a=-frace_1-frace_2.$

2.38. Показать, что тройка векторов $e_1(1,0,0), e_2(1,1,0)$ и $e_3(1,1,1)$ образуют базис в множестве всех векторов пространства. Вычислить координаты вектора $a=-2i-k$ в базисе $B(e_1, e_2, e_3)$ и написать соответствующее разложение вектора по базису.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

ГДЗ по геометрии 8 класс Атанасян рабочая тетрадь номер — 116

Авторы: Л.С. Атанасян , В.Ф. Бутузов , Ю.А. Глазков , И.И. Юдина .

Издательство: Просвещение 2016

Тип: Рабочая тетрадь

Подробный решебник (ГДЗ) по Геометрии за 8 (восьмой) класс рабочая тетрадь — готовый ответ номер — 116. Авторы учебника: Атанасян, Бутузов, Глазков, Юдина. Издательство: Просвещение 2016.

Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Похожие ГДЗ

ГДЗ учебник геометрия 7-9 класс Л.С. Атанасян

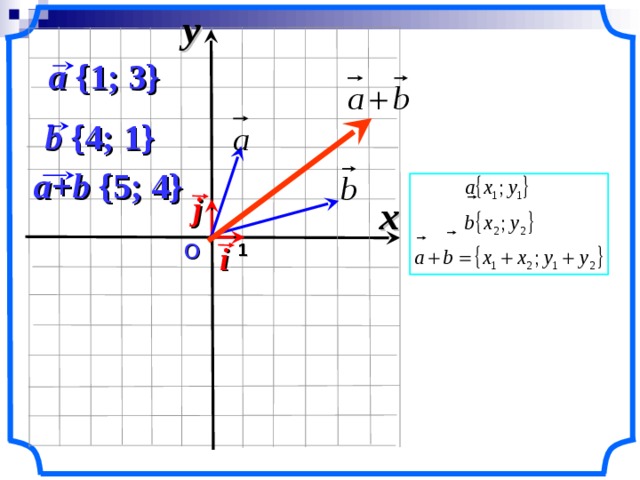
116.Используя правило треугольника, постройте векторы OA = а + b и СВ = а + b. Определите вид четырехугольника ОАВС.

🎬 Видео

1. Векторы и параллелограмм задачи №1Скачать

Площадь параллелограмма, построенного на данных векторахСкачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

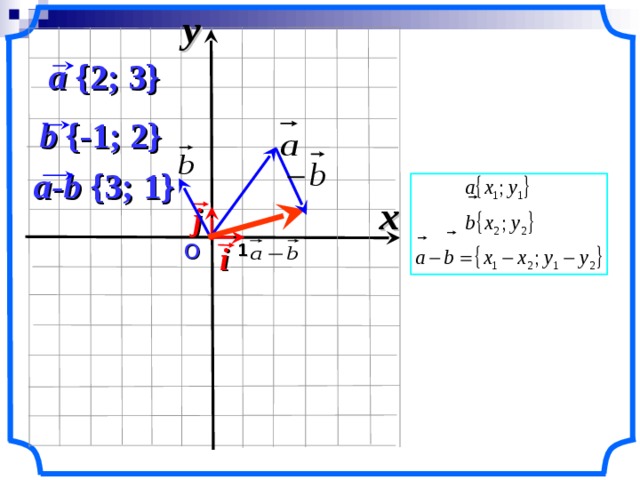
Вычитание векторов. 9 класс.Скачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

№369. Медианы грани ABC тетраэдра ОABC пересекаются в точке М. Разложите вектор ОАСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Площадь параллелограмма по векторамСкачать

Опорная задача о подобных треугольниках при пересечении высот | Планиметрия 84 | mathus.ru #егэ2024Скачать

№748. Диагонали параллелограмма ABCD пересекаются в точке O. Равны ли векторы?Скачать

Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

8 класс, 44 урок, Законы сложения векторов. Правило параллелограммаСкачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать