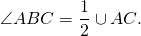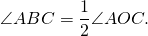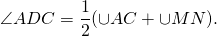Прямой угол в окружности (7 видео) | Курс школьной геометрии

Углы в окружности

Рассмотрим углы в окружности и углы, связанные с окружностью.

Угол с вершиной в центре окружности.
Угол с вершиной на окружности (его стороны пересекают окружность).
Угол с вершиной внутри окружности (не в центре).
Угол с вершиной вне окружности, стороны которого пересекают окружность.

I. Угол с вершиной в центре окружности называется центральным углом.

Стороны центрального угла разбивают окружность на две части. Дугой, соответствующей данному центральному углу, называется та часть, которая содержится внутри угла.

Например, центральному углу AOC соответствует дуга AC (или дуга AFC. Обычно дугу называют двумя буквами. Но, поскольку любую из двух, на которые точки A и C делят окружность, можно назвать AC, то третью, дополнительную букву, иногда используют для уточнения выбранной дуги).

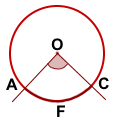
Градусная мера дуги окружности равна градусной мере соответствующего центрального угла:

II. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

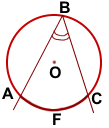
Стороны вписанного угла также разбивают окружность на две дуги. Говорят, что вписанный угол опирается на лугу, которая лежит внутри него.

Например, вписанный угол ABC опирается на дугу AC (или дугу AFC).

Вписанный угол равен половине дуги, на которую он опирается:

Есть другой вариант формулировки свойства вписанного угла.

Вписанный угол равен половине соответствующего ему центрального угла:

Вписанный угол, опирающийся на полуокружность — прямой.

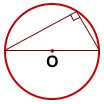
И наоборот: любой прямой вписанный угол опирается на полуокружность.

Другая формулировка этого утверждения:

(обратно: Если вписанный угол прямой, то он опирается на диаметр).

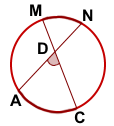
III. Угол, вершина которого лежит в окружности — это угол между пересекающимися хордами.

Угол между пересекающимися хордами равен полусумме дуг, заключённых между его сторонами и сторонами вертикального ему угла.

IV. Угол с вершиной вне окружности, обе стороны которого пересекают окружность — это угол между секущими, которые пересекаются вне окружности.

Угол между секущими, пересекающимися вне окружности, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами.

Содержание

Углы, связанные с окружностью
Вписанные и центральные углы
Теоремы о вписанных и центральных углах
Теоремы об углах, образованных хордами, касательными и секущими
Доказательства теорем об углах, связанных с окружностью
Центральные и вписанные углы
Центральный угол и вписанный угол
Свойства центральных и вписанных углов
Примеры решения задач
🔥 Видео

Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Углы, связанные с окружностью

Вписанные и центральные углы

Углы, образованные хордами, касательными и секущими

Доказательства теорем об углах, связанных с окружностью

Видео:Сопряжение острого углаСкачать

Вписанные и центральные углы

Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Теоремы о вписанных и центральных углах

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Фигура	Рисунок	Теорема
Вписанный угол
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
Вписанный угол		Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды
Вписанный угол		Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
Окружность, описанная около прямоугольного треугольника

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу равны.

Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды

Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Видео:Найти центр кругаСкачать

Теоремы об углах, образованных хордами, касательными и секущими

Вписанный угол

Окружность, описанная около прямоугольного треугольника

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами
Угол, образованный секущими, которые пересекаются вне круга
Угол, образованный касательной и хордой, проходящей через точку касания
Угол, образованный касательной и секущей
Угол, образованный двумя касательными к окружности

Угол, образованный пересекающимися хордами хордами

Формула:

Угол, образованный секущими секущими , которые пересекаются вне круга

Формула:

Угол, образованный касательной и хордой хордой , проходящей через точку касания

Формула:

Угол, образованный касательной и секущей касательной и секущей

Формула:

Угол, образованный двумя касательными касательными к окружности

Формулы:

Видео:Вписанные и центральные углыСкачать

Доказательства теорем об углах, связанных с окружностью

Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 8.

Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 9.

Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

Доказательство . Рассмотрим рисунок 10.

Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 11.

Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 12.

Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство

Видео:Построить прямой угол с помощью двусторонней линейки.Скачать

Центральные и вписанные углы

О чем эта статья:

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Видео:Центр кругаСкачать

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

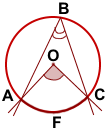
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?