Дан куб abcda1b1c1d1 найдите сумму векторов ab ad aa1 (4 видео)

Смешанное, векторное и скалярное произведение векторов

Задача:

Дан параллелепипед ABCDA₁B₁C₁D₁, построен на векторах AB(4,3,0), AD(2,1,2) и AA₁(-3,-2,5).
Найти:

Решение:

а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA₁). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.

(AB AD AA₁)

4	3	0
2	1	2
-3	-2	5

20 — 18 + 0 — 0 — 30 + 16

-12

Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
V_{ABCDA₁B₁C₁D₁}=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. S_ABCD= |[AB AD]|.

[AB AD]

i	j	k
4	3	0
2	1	2

6i — 8j — 2k

Теперь найдём модуль этого вектора:

S_ABCD= \|[AB AD]\|=√	(36+64+4)	=2√(26).

[AD AA₁]

i	j	k
2	1	2
-3	-2	5

9i — 16j — k

S_ADD₁A₁= |[AD AA₁]|=√(81+256+1)=13√2.

в) Что бы найти длину высоты, проведенной из вершины A₁ на грань ABCD, используем формулу для нахождения объема параллелепипеда V=h S_ABCD. С этой формулы видим:

V
S_ABCD

12
2√(26)

6
√(26)

3√(26)
13

г) Косинус угла λ₁, между ребром AB и диагональю B₁D будем высчитывать с помощью скалярного произведения векторов

cos(λ₁)

(AB B₁D)
\|AB\| * \|B₁D\|

Координаты вектора AB мы имеем, от вектор B₁D надо найти. Для этого используем следующую формулу:
B₁D = B₁A₁ + A₁A + AD = — AB — AA₁ + AD₁ = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B₁D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B₁D:
|AB|=√(16+9+0)=5, |B₁D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B₁D, (AB B₁D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:

cos(λ₁)

4
5√(10)

2√(10)
25

д) Что бы найти cos(λ₂), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD₁A₁ мы можем взять вектор [AD AA₁], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.

cos(λ₂)

69 + (-8)(-16) + (-2)*(-1)
2√(26) * 13√(2)

46√(13)
169

Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD₁A₁.

Геометрия. 10 класс

Сумма векторов

Видео:Правило параллелепипеда для векторовСкачать

В кубе назовите вектор, равный сумме $overrightarrow+overrightarrow <B_C_>+overrightarrow<DD_> $

Вектор в пространстве

Установите соответствие между выражением и вектором $Х$

Длина вектора

Дано: АВ = 3 ВС = 4 СС₁ = 12

Длина вектора АС₁ =

Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Длина вектора

Диагонали параллелепипеда пересекаются в точке О.

Варианты ответа (введите порядковый номер):

Вектор в пространстве

Упростите выражение и выберите правильный результат преобразования:

Вектор в пространстве

Видео:10 класс, 44 урок, Правило параллелепипедаСкачать

В тетраэдре ABCD точка Е — середина АD.

Докажите, что $overrightarrow=frac(overrightarrow+overrightarrow)$

Так как $overrightarrow+overrightarrow=0$, то $overrightarrow+overrightarrow=2overrightarrow$, значит $overrightarrow=frac(overrightarrow+overrightarrow)$

Сложим полученные равенства $overrightarrow+overrightarrow+overrightarrow+overrightarrow=2overrightarrow$

📸 Видео

№327. На рисунке 97 изображен параллелепипед ABCDA1B1C1D1. Назовите вектор, нСкачать

8 класс, 43 урок, Сумма двух векторовСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать

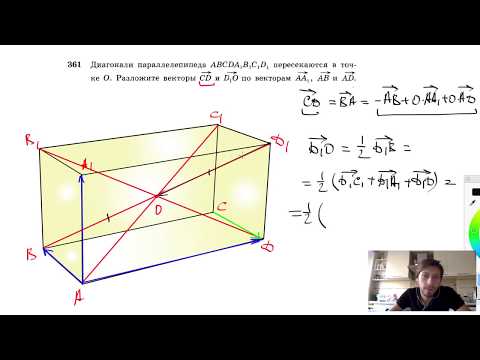
№361. Диагонали параллелепипеда ABCDA1B1C1D1 пересекаются в точке О. Разложите векторыСкачать

№364. Точка К—середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор АК по векторам а = АВ,Скачать

№344. Диагонали куба ABCDA1B1C1D1 пересекаются в точке О. Найдите число k такое,Скачать

10 класс, 41 урок, Сумма нескольких векторовСкачать

№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать

Задание 3 (№27717) ЕГЭ по математике. Урок 80Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

№355. Дан параллелепипед ABCDA1B1C1D1. Какие из следующих трех векторов компланарныСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

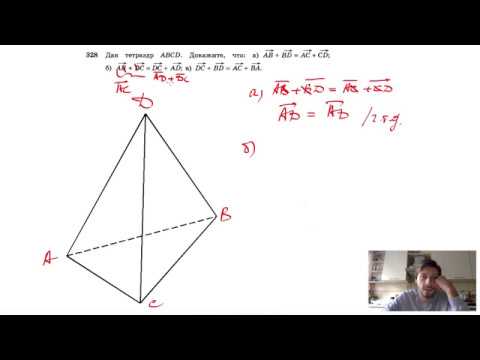
№328. Дан тетраэдр ABCD. Докажите, что: а) АВ + BD=AC + CD; б) AB + BC = DC + AD;Скачать

№170. Докажите, что треугольники ABC и А1B1С1 равны, если АВ =А1В1, ∠A=∠A1, AD =A1D1, где AD и A1D1Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать