Алгебра | 5 — 9 классы
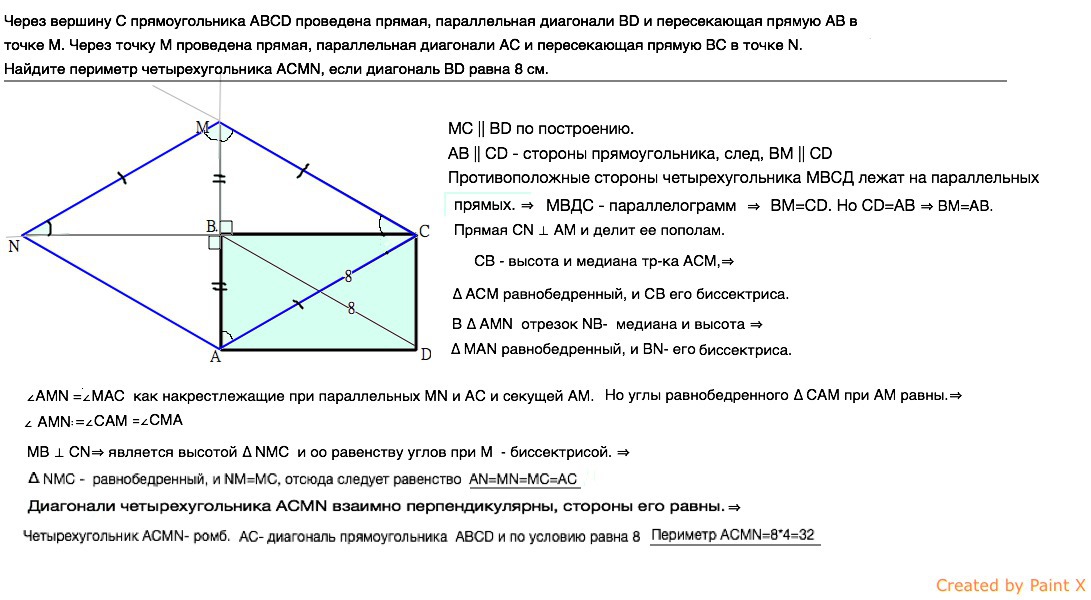
Через вершину C прямоугольника ABCD проведена прямая, параллельная диагонали BD и пересекающая пряму AB в точке M.
Через точку M проведена прямая, параллельная диагонали AC и пересекающая прямую BC в точке N.
Найдите периметр четырехугольника ACMN, если диагональ BD равна 8 см.
Прошу решене и чертёж).
Через вершину C прямоугольника ABCD проведена прямая, параллельная диагонали BD и пересекающая прямую AB в точке M.
Через точку M проведена прямая, параллельная диагонали AC и пересекающая прямую BC в точке N.
Найдите периметр четырехугольника ACMN, если диагональ BD равна 8 см
Казалось бы очевидно — сторонычетырехугольника ACMN равны между собой и равны диагоналям прямоугольника.
Тем не менее это нужно доказать.
МС║ВD по построению.
АВ║ СD — стороны прямоугольника, след, ВМ║СD
Противоположные стороны четырехугольника МВСД лежат на параллельных прямых.
Но СD = АВ⇒ ВМ = АВ.
СN⊥ АМ и делит ее пополам.
СВ — высота и медиана ∆ АСМ, ⇒
∆ АСМ равнобедренный, и СВ его биссектриса.
В ∆ АМN отрезок NB – медиана и высота⇒∆ МАN равнобедренный, и BN — его биссектриса.
AN = MN, a MN = MC = AC
∠АМN = ∠MАС как накрестлежащие при параллельных МN и АC и секущей АМ.
Но углы равнобедренного ∆ САМ при АМ равны.
МВ⊥ СN⇒ является высотой ∆ NMC и оо равенству углов при М — биссектрисой.
NMC — равнобедренный, и NM = MC, отсюда следует равенство AN = MN = MC = АС
Четырехугольник АСМN — ромб.
АС — диагональ прямоугольника ABCD и по условию равна 8
Периметр АСМN = 8 * 4 = 32.
- Через точку ( — 1 ; 1) проведена прямая, параллельно прямой y = 7x?
- Укажите номера верных утверждений :1) Если диагонали четырехугольника делятся точкой пересечения пополам, то этот четырехугольник трапеция?
- Даны две параллельные плоскости и точки A и B на одной из них?
- Прямоугольник пересекается 9 прямыми, параллельными одной его стороне, и 12 прямыми, параллельными другой?
- Прямая и парабола Пересекаются в точках А и В?
- Отметьте в тетради точки А и С проведите через них прямую?
- На точке не лежащей на прямой можно провести прямую параллельную этой прямой?
- Через точку А(1, 14) проведена прямая параллельна оси абсцисс, найдите ординату ее точки пересечения с осью Оу?
- Через вершину а ромба ABCD ТЦ проведена прямая А Параллельная диагонали BD А через вершину C прямая B не лежащая в плоскости ромба?
- Обозначьте точки АВС на одной прямой и через каждые две точки проведите прямую?
- Четырехугольники
- теория по математике 📈 планиметрия
- Выпуклый четырехугольник
- Виды и свойства выпуклых четырехугольников
- Прямоугольник
- Квадрат
- Параллелограмм
- Трапеция
- Виды трапеций
- Средняя линия трапеции
- Олимпиадные задания по математике 8 — 11 класс
- Олимпиадные задания по математике 8 — 11 класс
- Олимпиадные задания по математике 8 класс
- Олимпиадные задания по математике 8 класс
- Олимпиадные задания по математике 9 класс
- Олимпиадные задания по математике 9 класс
- Олимпиадные задания по математике 9 класс
- Олимпиадные задания по математике 10 класс
- Олимпиадные задания по математике 10 класс
- Олимпиадные задания по математике 11 класс
- Олимпиадные задания по математике 11 класс
Видео:№128. Через точку О пересечения диагоналей параллелограмма ABCD проведена прямаяСкачать

Через точку ( — 1 ; 1) проведена прямая, параллельно прямой y = 7x?
Через точку ( — 1 ; 1) проведена прямая, параллельно прямой y = 7x.
Найдите абсциссу точки пересечения этой прямой с осью Ox.
Видео:№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

Укажите номера верных утверждений :1) Если диагонали четырехугольника делятся точкой пересечения пополам, то этот четырехугольник трапеция?
Укажите номера верных утверждений :
1) Если диагонали четырехугольника делятся точкой пересечения пополам, то этот четырехугольник трапеция.
2) Диагонали ромба перпендикулярны.
3)Через данную точку можно провести не более одной прямой, параллельной данной.
4)Если диагонали четырехугольника равны, то этот четырехугольник параллелограмм.
Видео:№120. Через точку О пересечения диагоналей квадрата со стороной а проведена прямая ОКСкачать

Даны две параллельные плоскости и точки A и B на одной из них?
Даны две параллельные плоскости и точки A и B на одной из них.
Через эти точки проведены параллельные прямые пересекающие вторую плоскость в точках M и K.
Чему равен KM, если AB = 7см?
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Прямоугольник пересекается 9 прямыми, параллельными одной его стороне, и 12 прямыми, параллельными другой?
Прямоугольник пересекается 9 прямыми, параллельными одной его стороне, и 12 прямыми, параллельными другой.
Сколько всего получилось прямоугольников?
Видео:Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

Прямая и парабола Пересекаются в точках А и В?
Прямая и парабола Пересекаются в точках А и В.
Найдите координаты точки В.
Видео:№38. Через вершину А ромба ABCD проведена прямая а, параллельная диагонали BD,Скачать

Отметьте в тетради точки А и С проведите через них прямую?
Отметьте в тетради точки А и С проведите через них прямую.
Отметьте точку В лежащую на прямой АС и точку К не лежащую на прямой АС проведи луч с началом в точке К пересекающий отрезок АВ.
Видео:№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

На точке не лежащей на прямой можно провести прямую параллельную этой прямой?
На точке не лежащей на прямой можно провести прямую параллельную этой прямой?
Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Через точку А(1, 14) проведена прямая параллельна оси абсцисс, найдите ординату ее точки пересечения с осью Оу?
Через точку А(1, 14) проведена прямая параллельна оси абсцисс, найдите ординату ее точки пересечения с осью Оу.
Видео:№46. Прямая m параллельна диагонали BD ромба ABCD и не лежит в плоскости ромба.Скачать

Через вершину а ромба ABCD ТЦ проведена прямая А Параллельная диагонали BD А через вершину C прямая B не лежащая в плоскости ромба?
Через вершину а ромба ABCD ТЦ проведена прямая А Параллельная диагонали BD А через вершину C прямая B не лежащая в плоскости ромба.
Докажите что а)прямые а и Сд пересекаются ; б) а и б скрещивающиеся прямые.
Видео:Геометрия Дан четырехугольник ABCD в котором угол A = углу D угол B = углу C причем прямые AB и CDСкачать

Обозначьте точки АВС на одной прямой и через каждые две точки проведите прямую?
Обозначьте точки АВС на одной прямой и через каждые две точки проведите прямую.
Сколько прямых можно провестр.
Сколько прямых пересекающих.
Назовите точки пересечения.
Вопрос Через вершину C прямоугольника ABCD проведена прямая, параллельная диагонали BD и пересекающая пряму AB в точке M?, расположенный на этой странице сайта, относится к категории Алгебра и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Четырехугольники
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.

- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб – это параллелограмм, у которого все стороны равны.
Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.
Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.
углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.
Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.
Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.
Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.
Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.
Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить
На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).
Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).
Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:№403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметрСкачать

Олимпиадные задания по математике 8 — 11 класс
Видео:№748. Диагонали параллелограмма ABCD пересекаются в точке O. Равны ли векторы?Скачать

Олимпиадные задания по математике 8 — 11 класс
Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Олимпиадные задания по математике 8 класс
1. На доске была нарисована система координат и отмечены точки A(1;2) и B(3;1). Систему координат стерли. Восстановите ее по двум отмеченным точкам.
2. В некотором треугольнике биссектрисы двух внутренних углов продолжили до пересечения с описанной окружностью и получили две равные хорды. Верно ли, что треугольник равнобедренный?
3. В правильном шестиугольнике АВСDEF на прямой AF взята точка X так, что угол XСD = 45 o . Найдите угол FXE.
4. Около четырехугольника ABCD можно описать окружность. Точка p – основание перпендикуляра, опущенного из точки А на прямую ВС, Q – из А на DC, R – из D на АВ и Т – из D на ВС. Докажите, что точки p, Q, R и T лежат на одной окружности.
5. Восстановите остроугольный треугольник по ортоцентру и серединам двух сторон.
6. Противоположные стороны выпуклого шестиугольника ABCDEF параллельны. Назовем его «высотами» векторы с концами на прямых, содержащих противолежащие стороны, перпендикулярные им и направленные от AB к DE, от EF к BC и от CD к AF. Докажите, что вокруг этого шестиугольника можно описать окружность тогда и только тогда, когда сумма его «высот» равна нулевому вектору.
Видео:№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

Олимпиадные задания по математике 8 класс
1. Биссектриса угла В и биссектриса внешнего угла D прямоугольника ABCD пересекают сторону AD и прямую АВ в точках М и К соответственно. Докажите, что отрезок МК равен и перпендикулярен диагонали прямоугольника.
2. В равнобедренном треугольнике АВС на боковой стороне ВС отмечена точка М так, что отрезок СМ равен высоте треугольника, проведенной к этой стороне, а на боковой стороне АВ отмечена точка К так, что угол КМС – прямой. Найдите угол АСК .
3. Из листа бумаги в клетку вырезали квадрат 2×2. Используя только линейку без делений и не выходя за пределы квадрата, разделите диагональ квадрата на 6 равных частей.
4. В трапеции ABCD : AB = BC = CD , CH – высота. Докажите, что перпендикуляр, опущенный из Н на АС , проходит через середину BD .
5. Пусть AA 1 и BB 1 – высоты неравнобедренного остроугольного треугольника АВС , М – середина АВ . Окружности, описанные около треугольников AMA 1 и BMB 1 пересекают прямые АС и ВС в точках К и L соответственно. Докажите, что К , М и L лежат на одной прямой.
6. Один треугольник лежит внутри другого. Докажите, что хотя бы одна из двух наименьших сторон (из шести) является стороной внутреннего треугольника.
Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Олимпиадные задания по математике 9 класс
1. Постройте треугольник по стороне, противолежащему углу и медиане, проведенной к другой стороне ( исследование вопроса о количестве решений не требуется ).
2. В выпуклом четырехугольнике ABCD Ð ABC = 90 0 , Ð BAC = Ð CAD , AC = AD , DH — высота треугольника ACD . В каком отношении прямая BH делит отрезок CD ?
3. Внутри отрезка АС выбрана произвольная точка В и построены окружности с диаметрами АВ и ВС . На окружностях (в одной полуплоскости относительно АС ) выбраны соответственно точки M и L так, что Ð MBA = Ð LBC . Точки K и F отмечены соответственно на лучах ВМ и BL так, что BK = BC и BF = AB . Докажите, что точки M , K , F и L лежат на одной окружности.
4. В треугольнике ABC M — точка пересечения медиан, O — центр вписанной окружности, A’ , B’ , C’ — точки ее касания со сторонами BC , CA , AB соответственно. Докажите, что, если CA’ = AB , то прямые OM и AB перпендикулярны.
5. Дан треугольник АВС . Точка О 1 — центр прямоугольника ВСDE , построенного так, что сторона DE прямоугольника содержит вершину А треугольника. Точки О 2 и О 3 являются центрами прямоугольников, построенных аналогичным образом на сторонах АС и АВ соответственно. Докажите, что прямые АО 1 , ВО 2 и СО 3 пересекаются в одной точке.
6. На плоскости расположен круг. Какое наименьшее количество прямых надо провести, чтобы, симметрично отражая данный круг относительно этих прямых (в любом порядке конечное количество раз), можно было накрыть им любую заданную точку плоскости?
Видео:№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

Олимпиадные задания по математике 9 класс
9.1. В выпуклом четырехугольнике АВС D Е – середина CD , F – середина А D , K – точка пересечения АС и ВЕ . Докажите, что площадь треугольника BKF в два раза меньше площади треугольника АВС .
9.2. Постройте треугольник АВС по углу А и медианам, проведенным из вершин В и С .
9.3. Дан квадрат ABCD . Найдите геометрическое место точек M таких, что Ð AMB = Ð CMD .
9.4. Треугольник ABC вписан в окружность. Через точки A и B проведены касательные к этой окружности, которые пересекаются в точке p . Точки X и Y – ортогональные проекции точки p на прямые AC и BC . Докажите, что прямая XY перпендикулярна медиане треугольника ABC , проведенной из вершины C .
9.5. Диагонали вписанного четырёхугольника ABCD пересекаются в точке M , Ð AMB = 60 ° . На сторонах AD и BC во внешнюю сторону построены равносторонние треугольники ADK и BCL . Прямая KL пересекает описанную около ABCD окружность в точках p и Q . Докажите, что pK = LQ .
9.6. Длина каждой стороны и каждой не главной диагонали выпуклого шестиугольника не превосходит 1. Докажите, что в этом шестиугольнике найдется главная диагональ, длина которой не превосходит 2 деленное на корень из 3 .
Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Олимпиадные задания по математике 9 класс
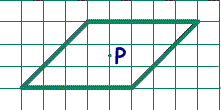
1. На рисунке изображен параллелограмм и отмечена точка p пересечения его диагоналей. Проведите через p прямую так, чтобы она разбила параллелограмм на две части, из которых можно сложить ромб.
2. Квадрат и прямоугольник одинакового периметра имеют общий угол. Докажите, что точка пересечения диагоналей прямоугольника лежит на диагонали квадрата.
4. Постройте треугольник по стороне, радиусу вписанной окружности и радиусу вневписанной окружности, касающейся этой стороны. (Исследование проводить не требуется.)
5. В некоторой точке круглого острова радиусом 1 км зарыт клад. На берегу острова стоит математик с прибором, который указывает направление на клад, когда расстояние до клада не превосходит 500 м. Кроме того, у математика есть карта острова, на которой он может фиксировать все свои перемещения, выполнять измерения и геометрические построения. Математик утверждает, что у него есть алгоритм, как добраться до клада, пройдя меньше 4 км. Может ли это быть правдой?
6. Фиксированы две окружности w1 и w2, одна их внешняя касательная l и одна их внутренняя касательная m. На прямой m выбирается точка X, а на прямой l строятся точки Y и Z так, что XY и XZ касаются w1 и w2 соответственно, а треугольник XYZ содержит окружности w1 и w2. Докажите, что центры окружностей, вписанных в треугольники XYZ , лежат на одной прямой.
Видео:Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 12, AB = 7. Найдите DO.Скачать

Олимпиадные задания по математике 10 класс
10.1. Е и F – середины сторон ВС и AD выпуклого четырехугольника АВС D . Докажите, что отрезок EF делит диагонали АС и BD в одном и том же отношении.
10.2. Существует ли в пространстве замкнутая самопересекающаяся ломаная, которая пересекает каждое свое звено ровно один раз, причем в его середине?
10.3. На доске была нарисована окружность с отмеченным центром, вписанный в нее четырехугольник, и окружность, вписанная в него, также с отмеченным центром. Затем стерли четырехугольник (сохранив одну вершину) и вписанную окружность (сохранив ее центр). Восстановите какую-нибудь из стертых вершин четырехугольника, пользуясь только линейкой и проведя не более шести линий.
10.4. В треугольнике АВС : М – точка пересечения медиан, О – центр вписанной окружности. Докажите, что если прямая ОМ параллельна стороне ВС , то точка О равноудалена от сторон АВ и АС .
10.5. Трапеция АВС D с основаниями AB и CD вписана в окружность. Докажите, что четырехугольник, образованный ортогональными проекциями любой точки этой окружности на прямые AC , BC , AD и BD , является вписанным.
10.6. В тетраэдре DABC : Ð ACB = Ð ADB , ( С D ) ^ ( АВС ). В треугольнике АВС дана высота h , проведенная к стороне АВ , и расстояние d от центра описанной окружности до этой стороны. Найдите длину CD .
Олимпиадные задания по математике 10 класс
1. Каждый из двух подобных треугольников разрезали на два треугольника так, что одна из получившихся частей одного треугольника подобна одной из частей другого треугольника. Верно ли, что оставшиеся части также подобны?
2. Даны радиусы r и R двух непересекающихся окружностей. Общие внутренние касательные этих окружностей перпендикулярны. Найдите площадь треугольника, ограниченного этими касательными, а также общей внешней касательной.
3. Дан четырехугольник ABCD. A’, B’, C’ и D’ – середины сторон BC, CD, DA и AB соответственно. Известно, что AA’ = CC’ и BB’ = DD’. Верно ли, что ABCD параллелограмм?
4. В треугольнике АВС угол А равен 120 o . Докажите, что расстояние от центра описанной окружности до ортоцентра равно АВ + АС.
6. Есть два платка: один в форме квадрата, другой – в форме правильного треугольника, причем их периметры одинаковы. Существует ли многогранник, который можно полностью оклеить этими двумя платками без наложений (платки можно сгибать, но нельзя резать)?
6. Дан треугольник ABC и точки p и Q. Известно, что треугольники, образованные проекциями p и Q на стороны ABC, подобны (соответствуют друг другу вершины, лежащие на одних и тех же сторонах исходного треугольника). Докажите, что прямая pQ проходит через центр описанной окружности треугольника ABC.
Олимпиадные задания по математике 11 класс
1. AD и BE – высоты треугольника АВС . Оказалось, что точка C’ , симметричная вершине С относительно середины отрезка DE , лежит на стороне AB . Докажите, что АВ – касательная к окружности, описанной около треугольника DEC’ .
2. Прямая а пересекает плоскость α . Известно, что в этой плоскости найдутся 2011 прямых, равноудаленных от а и не пересекающих a. Верно ли, что а перпендикулярна α ?
3. Дана неравнобокая трапеция ABCD ( AB || CD ). Произвольная окружность, проходящая через точки А и В , пересекает боковые стороны трапеции в точках p и Q , а диагонали – в точках M и N . Докажите, что прямые pQ , MN и CD пересекаются в одной точке.
4. Докажите, что любой жесткий плоский треугольник T площади меньше четырёх можно просунуть сквозь треугольную дырку Q площади 3.
5. В выпуклом четырехугольнике ABCD : AC ⊥ BD , ∠ BCA = 10°, ∠ BDA = 20°, ∠ BAC = 40°. Найдите ∠ BDC . ( Ответ выразите в градусах. )
6. Пусть AA 1, BB 1 и CC 1 – высоты неравнобедренного остроугольного треугольника АВС ; окружности, описанные около треугольников АВС и A 1 B 1 C , вторично пересекаются в точке Р , Z – точка пересечения касательных к описанной окружности треугольника АВС , проведённых в точках А и В . Докажите, что прямые АР , ВС и ZC 1 пересекаются в одной точке.
Олимпиадные задания по математике 11 класс
1. Существуют ли два таких четырехугольника, что стороны первого меньше соответствующих сторон второго, а соответствующие диагонали больше?
2. Трапеция ABCD и параллелограмм MBDK расположены так, что стороны параллелограмма параллельны диагоналям трапеции (см. рис.). Докажите, что площадь зеленой части равна сумме площадей синих частей.
3. В остроугольном треугольнике АВС проведены высоты АА1 и ВВ1. Докажите, что перпендикуляр, опущенный из точки касания вписанной окружности со стороной ВС на прямую АС, проходит через центр вписанной окружности треугольника А1СВ1.
4. На медианах треугольника как на диаметрах построены три окружности. Известно, что они попарно пересекаются. Пусть C1 — более удаленная от вершины C точка пересечения окружностей, построенных на медианах AM1 и BM2. Точки A1 и B1 определяются аналогично. Докажите, что прямые АА1, ВВ1 и СС1 пересекаются в одной точке.
5. Докажите, что у любого выпуклого многогранника найдутся три ребра, из которых можно составить треугольник.
6. К двум окружностям w1 и w2, пересекающимся в точках А и В, проведена их общая касательная CD (C и D — точки касания соответственно, точка B ближе к прямой CD, чем А). Прямая, проходящая через А, вторично пересекает w1 и w2 в точках К и L соответственно (A лежит между K и L). Прямые KC и LD пересекаются в точке p. Докажите, что РВ — симедиана треугольника KpL (прямая, симметричная медиане относительно биссектрисы).
Олимпиадные задания по математике для учащихся 1-11 классов с решением и ответами: