Дуга окружности это часть окружности выделенная точками (3 видео)

Окружность

Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.

Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:

Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:

Содержание

Построение окружности циркулем
Радиус, хорда и диаметр
Урок по геометрии для 7 класса «Окружность и ее элементы»
«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
ТАБЛИЦА № 1
Краткое описание документа:
Окружность и круг
теория по математике 📈 планиметрия
Определения
Свойство хорд
Длина окружности
Дуга, касательная, круг, сектор, сегмент
Свойства касательной
💥 Видео

Видео:Длина дуги окружности. 9 класс.Скачать

Построение окружности циркулем

Для построения окружности используют специальный прибор — циркуль:

Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Радиус, хорда и диаметр

Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:

Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.

Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.

Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:

Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:

Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:

Для обозначения дуг используется символ :

AFB — дуга с концами в точках A и B, содержащая точку F;
AJB — дуга с концами в точках A и B, содержащая точку J.

О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.

Хорда AB стягивает дуги AFB и AJB.

Видео:8 класс, 33 урок, Градусная мера дуги окружностиСкачать

Урок по геометрии для 7 класса «Окружность и ее элементы»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Радиус и диаметрСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Урок: Геометрия 7 класс.

Тема: Окружность И ЕЕ ЭЛЕМЕНТЫ.

Цели урока: 1. Систематизировать знания учащихся по теме окружность и ее элементы;

2. Совершенствование навыка решения задач по теме.

3. Развитие памяти, внимания, мышления.

4. Воспитание интереса к предмету.

Фронтальный опрос. Блиц-опрос.

— что такое геометрия?

— что такое отрезок?

— какие отрезки называем равными?

— что такое угол? Виды углов? Биссектриса угла?

— смежные, вертикальные углы?

— какие прямые знаете?

— параллельные, перпендикулярные, пересекающиеся прямые?

-Треугольник. Виды треугольников?

— сумма внутренних углов треугольника?

3. Введение в тему.

Решите ребус, разгадав его, вы узнаете тему урока.

4. Работа по теме.

Сегодня мы с вами продолжим изучение темы окружность. Давайте вспомним, что же такое окружность? Назовите элементы окружности?

Окружность – геометрическая фигура …,все точки которой находятся на

заданном расстоянии от центра.

Круг- это часть плоскости …, ограниченная окружностью.

Радиус – это отрезок . соединяющий центр окружности с

любой точкой окружности.

Диаметр- это отрезок, соединяющий … две точки окружности и проходящий

Хорда- это отрезок, соединяющий …две точки окружности.

Диаметр – это хорда, … проходящая через центр.

Центральный угол – это угол … образованный двумя радиусами.

Дуга окружности – это … часть окружности, ограниченная двумя точками.

5. Самостоятельная работа.

А теперь повторив определения геометрических понятий, мы с вами поработаем индивидуально. Для каждого из понятий необходимо подобрать соответствующий ему рисунок (таблица №1). Таблица выдается каждому ученику.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

ТАБЛИЦА № 1

По заданному рисунку назвать все элементы окружности.

6. Решение задач. Работа у доски.

Давайте вспомним взаимное расположение прямой и окружности.

Что такое касательная к окружности?

Что такое секущая?

Дано: окружность с центром О,

АС- касательная, АВ- хорда, угол ВАС=75 о

В Найти: Угол АОВ

О 1) 90 0 – 75 0 =15 0 (угол А в треугольнике АОВ)

2)180 0 -15 0 *2=150 0 ( угол АОВ)

Дано: окружность с центром О.

ОА – радиус окружности.

Центральный угол АОС = 70 градусам.

Устно в учебнике стр 68 № 237

7. Самостоятельная работа. Задачи на построение.

1. Отметьте в тетради точку О. Постройте окружность с центром в этой точке.

Измерьте радиус окружности. Чему равен ее диаметр?

постройте хорду этой окружности. Найдите расстояние от центра до хорды.

1. Отметьте в тетради точку О. Постройте окружность с центром в этой точке.

2. Отрезки АВ и С D – диаметры окружности с центром О. Найдите периметр треугольника АО D , если СВ = 13 см, АВ = 16 см.

8. Закрепление полученных знаний. Тест.

Тест «Окружность и ее элементы»

Вычеркнуть ненужные слова текста в скобках:

а) Окружность – это (абстрактная, геометрическая, плоская) фигура, состоящая из (множества, всех) точек, расположенных на (одинаковом, заданном) расстоянии от (некоторой, центральной) точки.

б) Радиусом окружности называется (линия, прямая, отрезок), соединяющая центр окружности с (заданной, какой-либо) точкой окружности.

Выбрать правильный ответ

Диаметр окружности – это …

а) два радиуса, лежащие на одной прямой;

б) хорда, проходящая через центр окружности;

в) прямая, проходящая через две точки и центр окружности.

Центр окружности – это …

а) точка, куда ставится ножка циркуля при начертании окружности;

б) середина окружности;

в) точка, равноудаленная от всех точек окружности.

Дуга окружности – это …

а) часть окружности, выделенная точками;

б) часть окружности, ограниченная двумя точками;

в) часть окружности, ограниченная хордой.

Определить, на сколько дуг делят окружность две точки, лежащие на окружности.

а) на одну; б) на две.

Как изображается хорда на чертеже окружности?

а) прямой линией; б) дугой окружности; в) отрезком с концами, лежащими на окружности.

Как называется отрезок, соединяющий центр окружности с любой точкой окружности?

а) длина окружности; б) радиус окружности; в) половина диаметра окружности.

Выбрать на рисунке хорду:

Выбрать на рисунке диаметр

9. Подведение итогов урока.

Понравился вам урок или нет? Чем мы занимались на уроке? Что вызвало интерес? Что удалось на уроке? Что было трудным, чего не удалось достичь? Как бы вы себя оценили?

10. домашнее задание.

Начертите окружность радиусом 6 см. Отметьте на окружности т. A , B , K , P , M , N , O так, чтобы были:

КГУ «Веселовская средняя общеобразовательная школа»

Разработка открытого урока

по геометрии в 7 классе на тему :

«Окружность и ее элементы»

2013-2014 учебный год

Краткое описание документа:

Тема: Окружность И ЕЕ ЭЛЕМЕНТЫ. Цели урока: 1. Систематизировать знания учащихся по теме окружность и ее элементы; 2. Совершенствование навыка решения задач по теме. 3. Развитие памяти, внимания, мышления. 4. Воспитание интереса к предмету. Ход урока Организационный момент. Фронтальный опрос. Блиц-опрос. — что такое геометрия? — что такое отрезок? — какие отрезки называем равными? — что такое угол? Виды углов? Биссектриса угла? — смежные, вертикальные углы? — какие прямые знаете? — параллельные, перпендикулярные, пересекающиеся прямые? -Треугольник. Виды треугольников? — сумма внутренних углов треугольника? — равенство фигур? 3. Введение в тему. Решите ребус, разгадав его, вы узнаете тему урока. (окружность) 4. Работа по теме. Сегодня мы с вами продолжим изучение темы окружность. Давайте вспомним, что же такое окружность? Назовите элементы окружности? Окружность – геометрическая фигура …,все точки которой находятся на заданном расстоянии от центра. Круг- это часть плоскости …, ограниченная окружностью. Радиус – это отрезок . соединяющий центр окружности с любой точкой окружности. Диаметр- это отрезок, соединяющий … две точки окружности и проходящий через центр. Хорда- это отрезок, соединяющий …две точки окружности. Диаметр – это хорда, … проходящая через центр. Центральный угол – это угол … образованный двумя радиусами. Дуга окружности – это … часть окружности, ограниченная двумя точками. 5. Самостоятельная работа. А теперь повторив определения геометрических понятий, мы с вами поработаем индивидуально. Для каждого из понятий необходимо подобрать соответствующий ему рисунок (таблица №1). Таблица выдается каждому ученику. ТАБЛИЦА № 1 По заданному рисунку назвать все элементы окружности. 6. Решение задач. Работа у доски. Давайте вспомним взаимное расположение прямой и окружности. Что такое касательная к окружности? Что такое секущая? Задача №1 Дано: окружность с центром О, АС- касательная, АВ- хорда, угол ВАС=75о В Найти: Угол АОВ Решение: О 1) 900 – 750 =150 (угол А в треугольнике АОВ) 2)1800 -150 *2=1500 ( угол АОВ) А С Задача №2. Дано: окружность с центром О. ОА – радиус окружности. АС – хорда. Центральный угол АОС = 70 градусам. Найти угол ОАС -? Устно в учебнике стр 68 № 237 7. Самостоятельная работа. Задачи на построение. Разноуровневые задания. 1 вариант. 1. Отметьте в тетради точку О. Постройте окружность с центром в этой точке. Измерьте радиус окружности. Чему равен ее диаметр? 2. постройте хорду этой окружности. Найдите расстояние от центра до хорды. 2 вариант. 1. Отметьте в тетради точку О. Постройте окружность с центром в этой точке. 2. Отрезки АВ и СD – диаметры окружности с центром О. Найдите периметр треугольника АОD, если СВ = 13 см, АВ = 16 см. 8. Закрепление полученных знаний. Тест. Тест «Окружность и ее элементы» 1) Вычеркнуть ненужные слова текста в скобках: а) Окружность – это (абстрактная, геометрическая, плоская) фигура, состоящая из (множества, всех) точек, расположенных на (одинаковом, заданном) расстоянии от (некоторой, центральной) точки. б) Радиусом окружности называется (линия, прямая, отрезок), соединяющая центр окружности с (заданной, какой-либо) точкой окружности. Выбрать правильный ответ 2) Диаметр окружности – это … а) два радиуса, лежащие на одной прямой; б) хорда, проходящая через центр окружности; в) прямая, проходящая через две точки и центр окружности. 3) Центр окружности – это … а) точка, куда ставится ножка циркуля при начертании окружности; б) середина окружности; в) точка, равноудаленная от всех точек окружности. 4) Дуга окружности – это … а) часть окружности, выделенная точками; б) часть окружности, ограниченная двумя точками; в) часть окружности, ограниченная хордой. 5) Определить, на сколько дуг делят окружность две точки, лежащие на окружности. а) на одну; б) на две. 6) Как изображается хорда на чертеже окружности? а) прямой линией; б) дугой окружности; в) отрезком с концами, лежащими на окружности. 7) Как называется отрезок, соединяющий центр окружности с любой точкой окружности? а) длина окружности; б) радиус окружности; в) половина диаметра окружности. 8) Выбрать на рисунке хорду: а) ОА; б) ВО; в) СD. 9) Выбрать на рисунке диаметр а) MK; б) KN; в) OD. 9. Подведение итогов урока. Синквейн. Рефлексия. Понравился вам урок или нет? Чем мы занимались на уроке? Что вызвало интерес? Что удалось на уроке? Что было трудным, чего не удалось достичь? Как бы вы себя оценили? Оценки за урок. 10. домашнее задание. Начертите окружность радиусом 6 см. Отметьте на окружности т. A, B, K, P, M, N, O так, чтобы были: a) AK-хорда; b) KM-хорда; c) OM-радиус; d) KB-диаметр; e) BP-хорда; f) NK-хорда; g) AB-хорда; h) NP-диаметр.

Видео:Длина окружности. Математика 6 класс.Скачать

Окружность и круг

теория по математике 📈 планиметрия

Определения

Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.

На рисунке центр окружности обозначен точкой О. 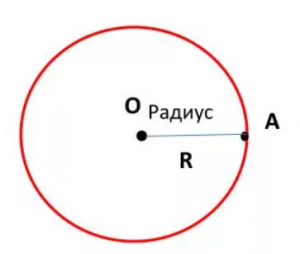Определения

Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.

Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.

Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.

Свойство хорд

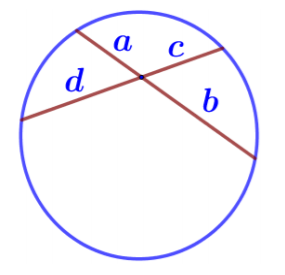
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.

Длина окружности

Длину окружности можно вычислить по формуле:

C=2πR, где π=3,14.

Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Дуга, касательная, круг, сектор, сегмент

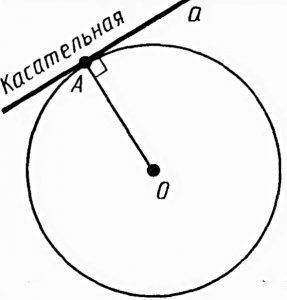
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).

Свойства касательной

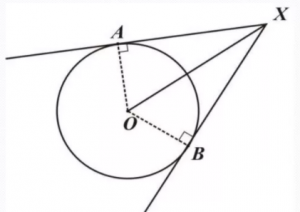
На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.

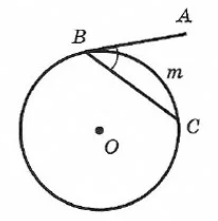
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.

Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.

Площадь круга вычисляется по формуле:

S=πR 2 , где π=3,14.

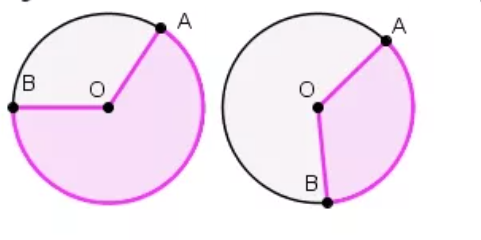
Сектор и его площадь

Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.

Площадь кругового сектора вычисляется по формуле:

S= π R 2 360 . . × α , где α – угол между радиусами.

Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.