Математика для школьников и студентов, обучение и образование
Видео:Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать

Точка Жергонна, теорема Жергонна

В 1810 году Жергонн начал издавать свой журнал, который имел официальное название Annales de mathématiques pures et appliquées, но стал известен как Annales de Gergonne. Этот журнал издавался в течение 22 лет, в основном в нем печатались работы, посвященные геометрии как основной области интересов Жергонна. В нем печатались работы многих известных математиков: Понселе, Плюкера, Брианшона, Галуа и др.
Жергонн дал элегантное решение задачи Аполлония: построить окружность, которая касается трех данных окружностей. Он ввел термин “поляра” и принцип двойственности в проективную геометрию.
Вот так Жергонн говорил о математических теориях:
“Невозможно чувствовать удовлетворение от того, что в некоторой теории сказано все, пока она не может быть объяснена в нескольких словах любому прохожему, с которым вы встретитесь на улице.’’
Красиво, не правда ли? Жаль, что это невозможно…
Определение. Точкой Жергонна называется точка пересечения отрезков, которые соединяют вершины треугольника с точками касания сторон, противоположных этим вершинам, и вписанной в треугольник окружности.
Пусть точка 








Докажем, что эти три отрезка действительно пересекаются в одной точке. Заметим, что центр вписанной окружности — это точка пересечения биссектрис углов треугольника 









Произведения 

следовательно, отношение этих произведений равно 
Замечание. Отрезок, соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой.
Теорема Жергонна. Пусть три чевианы 



1)
2)

Доказательство. Поскольку выполняются очевидные равенства
то равенства 1) и 2) эквивалентны. Докажем первое из них.
Рассмотрим отношения площадей треугольников
Здесь мы используем тот факт, что отношения площадей треугольников, имеющих общую сторону, равны отношениям их высот. Соответственно, отношение высот будет равно отношению длин параллельных отрезков, проведенных к общей стороне из противоположной вершины.
Видео:Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

Точка Жергонна треугольника.
Теорема.
Три чевианы, соединяющие вершины треугольника с точками пересечения вписанной окружности и сторон треугольника, пересекаются в одной точке.
Доказательство.
Пусть D, E, F — точки пересечения вписанной окружности и сторон треугольника BC, AC и AB соответственно.
AF=AE, BF=BD, CD=CE (свойство отрезков касательных, проведенных из одной точки, к окружности).
По теореме Чевы отрезки AD, BE и СF пересекаются в одной точке.
Точка Жергонна — точка пересечения чевиан треугольника, соединяющих вершины треугольника с точками пересечения вписанной окружности и сторон треугольника.
Теорема Жергонна.
Пусть G — точка Жергонна треугольника ABC и D, E, F — точки пересечения вписанной окружности и сторон треугольника BC, AC и AB соответственно. Тогда выполняются следующие равенства:
Видео:4.3 Пересечение отрезков. "Поколение Python": курс для начинающих. Курс StepikСкачать

«Замечательные точки треугольника. Точка Жергонна»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
«Замечательные точки треугольника. Точка Жергонна»
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Медианы треугольника пересекаются в одной точке . Она является в треугольнике центром тяжести – центроид.
Точка пересечения медиан делит каждую из медиан в отношении 2:1 , считая от вершины треугольника.
Биссектрисой треугольника называется луч, исходящий из вершины угла и делящий его на два равных угла.
Биссектрисы треугольника пересекаются в точке O , которая равноудалена от трех сторон треугольника и потому является центром вписанной в треугольник окружности (инцентр).
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Прямые, содержащие высоты треугольника, пересекаются в одной точке , она называется ортоцентром треугольника.
В треугольнике три медианы, три высоты, три биссектрисы, три серединных перпендикуляра.
Окружность, которая проходит через все три вершины треугольника называется описанной .
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке – центр описанной окружности.
Окружность внутри треугольника, касающаяся всех его сторон называется вписанной .
Замечание. Отрезок, соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой .
Рассмотрим треугольник АВС и отметим на его сторонах АВ, ВС и СА точки , , . Поставим такой вопрос: при каком расположении этих точек отрезки А, В и С пересекаются в одной точке?
Ответ на поставленный вопрос дает теоремы Джованни Чевы (1648-1734)
Теорема Чевы: Если на сторонах АВ, ВС и СА треугольника АВС взяты
соответственно точки , , , то отрезки А, В и С (чевианы) пересекаются в одной точке тогда и только тогда когда
Доказательство:
Пусть отрезки А, В и С пересекаются в одной точке О. Докажем, что выполнено равенство (1). По теореме о пропорциональных отрезках в треугольнике имеем:
Левые части этих равенств одинаковы, значит, равны и правые части. Приравнивая их, получаем
Разделив обе части на правую часть, приходим к равенству (1).
Докажем обратное утверждение. Пусть точки , , взяты на сторонах АВ, ВС и СА так, что выполнено равенство (1). Докажем, что отрезки А, В и С пересекаются в одной точке. Обозначим буквой О точку пересечения отрезков А и В и проведем прямую СО. Она пересекает сторону АВ в некоторой точке, которую обозначим . Так как отрезки А, В и С пересекаются в одной точке, то по доказанному в первом пункте
Итак, имеют место равенство (1) и (2).
Сопоставляя их, приходим к равенству =, которое показывает, что точки и делят сторону АВ в одном и том же отношении. Следовательно, точки и совпадают, и, значит, отрезки А, В и С пересекаются в точке О.
Применим данную теорему к центроиду – точке пересечения медиан треугольника.
По теореме Чевы: , значит медианы пересекаются в одной точке.
Оказывается если соединить вершины треугольника с противоположными точками касания вписанной окружности, то эти прямые пересекаются в одной точке. Это и есть точка Жергонна!
Определение. Точку пересечения прямых, соединяющих вершины
треугольника с точками касания вписанной окружности, называют точкой Жергонна.
Пусть точка 
Докажем, что чевианы AD , BE и CF пересекаются в одной точке.
Рассмотрим треугольник АВС:
FB = BD = y отрезки касательных к окружности, проведенные из одной
CE = CD = z точки
Воспользуемся теоремой Чевы:
— следовательно, по теореме Чевы эти отрезки пересекаются в одной точке.
Задача 1(Теорема Жергонна).
Пусть три чевианы AD , BE и CF пересекаются в точке 
1)
а) Рассмотрим отношения площадей треугольников. Запишем следующие равенства:
Здесь мы используем тот факт, что отношения площадей треугольников, имеющих общую сторону, равны отношениям их высот. Соответственно, отношение высот будет равно отношению длин параллельных отрезков, проведенных к общей стороне из противоположной вершины. Сложив эти равенства, получим:
Задача 2. В треугольнике АВС АВ= a , ВС= b , CA = c и
(полупериметр). Точки F , D , E – точки касания треугольника и вписанной окружности. Найти отрезки AF , FB , BD , DC , CE , EA .
Решение:
Рассмотрим треугольник АВС:
обозначим FB = BD = y отрезки касательных к окружности,
CE = CD = z проведенные из одной точки
(нашли отрезки CE и CD ).
(нашли отрезки AF и AE ).
(нашли отрезки FB и BD ).
Ответ: AF = AE =, FB = BD =, CE = CD =.
Задача 3.(олимпиадная задача)
В треугольной пирамиде проведены три биссектрисы плоских углов при вершине пирамиды, а также три биссектрисы основания пирамиды. Известно, что основания двух пар проведенных биссектрис совпадают. докажите, что основания и третьей пары биссектрис совпадают.
Пусть SABC – данная пирамида, SK , SL , SM – биссектрисы боковых граней SBC , SCA , SAB .
Тогда, По свойству биссектрис(отношение отрезков, на которые биссектриса делит сторону, равно отношению сответствующих сторон):
Перемножим левые и правые части этихравенств:
Следовательно, по теореме Чевы отрезки AK , BL , CM пересекаются в одной точке.
По условию, два отрезка есть биссектрисы углов в треугольнике ABC .
Три отрезка пересекаются в одной точке(доказано).Биссетрисы треугольника пересекаются в одной точке, значит и третий отрезок является биссектрисой.
📸 Видео
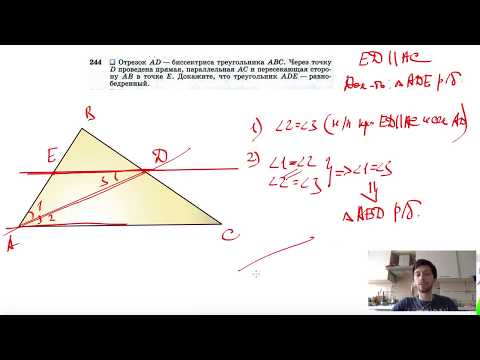
№244. Отрезок AD — биссектриса треугольника ABC. Через точку D проведена прямая, параллельная АССкачать
Пересечение прямой и отрезкаСкачать

ПЕРЕСЕЧЕНИЕ ВЫСОТ треугольника ТЕОРЕМА 8 класс АтанасянСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Алгоритмы. Пересечение отрезков.Скачать

Пересечения прямых, лучей, отрезковСкачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

ОТРЕЗОК ВНУТРИ ОКРУЖНОСТИ. Cherche la femme (фр)!Скачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Линия пересечения плоскостейСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Секретный прием в геометрии и при нем ЗадачаСкачать

Новое доказательство пересечения высот треугольника в одной точкеСкачать















