- теория по физике 🧲 колебания и волны
- Как появляются и распространяются электромагнитные волны
- Условия возникновения электромагнитных волн
- Плотность потока электромагнитного излучения
- Точечный источник излучения
- Зависимость плотности потока излучения от частоты
- Свойства электромагнитных волн
- Шкала электромагнитных волн
- 2.6. Электромагнитные волны
- Уравнения электромагнитной волны
- 💥 Видео
теория по физике 🧲 колебания и волны
Вспомним, что волна — это колебания, распространяющиеся в пространстве. Механическая волна представляет собой колебания, распространяющиеся в вещественной среде. Тогда электромагнитная волна — это электромагнитные колебания, которые распространяются в электромагнитном поле.
Видео:Что такое электромагнитная волна | Физика 11 класс #19 | ИнфоурокСкачать

Как появляются и распространяются электромагнитные волны
Представьте себе неподвижный точечный заряд. Пусть его окружают еще много таких зарядов. Тогда он будет действовать на них с некоторой кулоновской силой (и они на него). А теперь представьте, что заряд сместился. Это приведет к изменению расстояния по отношению к другим зарядам, а, следовательно, и к изменению сил, действующих на них. В результате они тоже сместятся, но с некоторым запаздыванием. При этом начнут смещаться и другие заряды, которые взаимодействовали с ними. Так распространяется электромагнитные взаимодействия.
Теперь представьте, что заряд не просто сместился, а он начал быстро колебаться вдоль одной прямой. Тогда по характеру движения он будет напоминать шарик, подвешенный к пружине. Разница будет только в том, что колебания заряженных частиц происходят с очень высокой частотой.
Вокруг колеблющегося заряда начнет периодически изменяться электрическое поле. Очевидно, что период изменений этого поля, будет равен периоду колебаний заряда. Периодически меняющееся электрическое поле будет порождать периодически меняющееся магнитное поле. Это магнитное поле, в свою очередь, будет создавать переменное электрическое поле, но уже на большем расстояние от заряда, и т.д. В результате появления взаимно порождаемых полей в пространстве, окружающем заряд, возникает система взаимно перпендикулярных, периодически меняющихся электрических и магнитных полей. Так образуется электромагнитная волна, которая распространяется от колеблющегося заряда во все стороны.
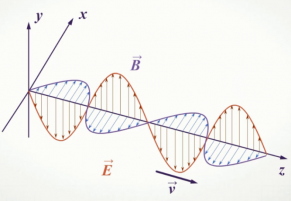
Электромагнитная волна не похожа на те возмущения вещественной среды, которые вызывают механические волны. Посмотрите на рисунок. На нем изображены векторы напряженности → E и магнитной индукции → B в различных точках пространства, лежащих на оси Oz, в фиксированный момент времени. Никаких гребней и впадин среды при этом не появляется.
В каждой точке пространства электрические и магнитные пол меняются во времени периодически. Чем дальше расположена точка от заряда, тем позднее ее достигнут колебания полей. Следовательно, на разных расстояниях от заряда колебания происходят с различными фазами. Колебания векторов → E и → B в любой точке совпадают по фазе.
Длина электромагнитной волны — расстояние между двумя ближайшими точками, в которых колебания происходят в одинаковых фазах.
Длина электромагнитной волны обозначается как λ. Единица измерения — м (метр).
Обратите внимание на рисунок выше. Векторы магнитной индукции и напряженности поля, являющиеся периодически изменяющимися величинами, в любой момент времени перпендикулярны направлению распространения волны. Следовательно, электромагнитная волна — поперечная волна.
Видео:Электромагнитные волны. Поток энергии. Вектор Умова-Пойтинга.Скачать

Условия возникновения электромагнитных волн
Электромагнитные волны излучаются только колеблющимися заряженными частицами. При этом важно, чтобы скорость их движения постоянно менялась, т.е. чтобы они двигались с ускорением.
Наличие ускорения — главное условие возникновения электромагнитных волн.
Электромагнитное поле может излучаться не только колеблющимся зарядом, но и заряженной частицей, перемещающейся с постоянно меняющейся скоростью. Интенсивность электромагнитного излучения тем больше, чем больше ускорение, с которым движется заряд.
Представим заряд, движущийся с постоянной скоростью. Тогда создаваемые им электрическое и магнитное поля будут сопровождать его как шлейф. Только при ускорении заряда поля «отрываются» от частицы и начинают самостоятельное существование в форме электромагнитных волн.
Впервые существование электромагнитных волн предположил Максвелл, который посчитал, что они должны распространяться со скоростью света. Но экспериментально они были обнаружены лишь спустя 10 лет после смерти ученого. Их открыл Герц. Он же подтвердил, что скорость распространения электромагнитных волн равна скорости света: c = 300 000 км/с.
Видео:Урок №45. Электромагнитные волны. Радиоволны.Скачать

Плотность потока электромагнитного излучения
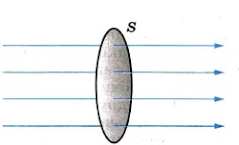
Излученные электромагнитные волны несут с собой энергию. Рассмотрим поверхность площадью S, через которую электромагнитные волны переносят энергию.
На рисунке выше прямые линии указывают направления распространения электромагнитных волн. Это лучи — линии, перпендикулярные поверхностям, во всех точках которых колебания происходят в одинаковых фазах. Такие поверхности называются волновыми поверхностями.
Плотность потока электромагнитного излучения, или интенсивность волны — отношение электромагнитной энергии ΔW, проходящей за время Δt через перпендикулярную лучам поверхность площадью S, к произведению площади S на время Δt.
Плотность потока электромагнитного излучения обозначается как I. Единица измерения — Вт/м 2 (ватт на квадратный метр). Поэтому плотность потока электромагнитного излучения фактически представляет собой мощность электромагнитного излучения, проходящего через единицу площади поверхности.
Численно плотность потока электромагнитного излучения определяется формулой:
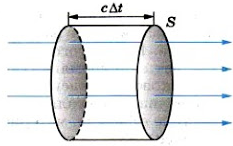
Выразим I через плотность электромагнитной энергии и скорость ее распространения с. Выберем поверхность площадью S, перпендикулярную лучам, и построим на ней как на основании цилиндр с образующей cΔt (см. рисунок ниже).
Объем цилиндра: ΔV = ScΔt. Энергия электромагнитного поля внутри цилиндра равна произведению плотности энергии на объем: ΔW = w cΔtS. Вся эта энергия за время Δt пройдет через правое основание цилиндра. Поэтому получаем:
I = w c Δ t S S Δ t . . = w c
Следовательно, плотность потока электромагнитного излучения равна произведению плотности электромагнитной энергии на скорость ее распространения.
Плотность электромагнитной энергии — энергия электромагнитного излучения в единице объема. Обозначается как w. Единица измерения — Дж/м 3 .
Пример №1. Плотность потока излучения равна 6 мВт/м 2 . Найти плотность энергии электромагнитной волны.
w = I c . . = 6 · 10 − 3 3 · 10 8 . . = 2 · 10 − 11 ( Д ж м 3 . . )
Точечный источник излучения
Источники излучения электромагнитных волн могут быть весьма разнообразными. Простейшим является точечный источник.
Точечный источник — источник излучения, размеры которого много меньше расстояния, на котором оценивается его действие.
Предполагается, что точечный источник посылает электромагнитные волны по всем направлениям с одинаковой интенсивностью. В действительности таких источников не существует. Но за такие источники излучения можно принять звезды, так как расстояние между ними существенно больше размеров самих звезд.
Энергия, которую переносят электромагнитные волны, с течением времени распределяется по все большей и большей поверхности. Поэтому энергия, передаваемая через поверхность единичной площадки за единицу времени, т. е. плотность потока излучения, уменьшается по мере удаления от источника.
Поместим точечный источник в центр сферы радиусом R. Площадь поверхности сферы S = 4πR 2 . Если считать, что источник по всем направлениям за время Δt излучает суммарную энергию ΔW, получим:
I = Δ W S Δ t . . = Δ W 4 π Δ t . . · 1 R 2 . .
Плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника.
Пример №2. Плотность потока электромагнитного излучения на расстоянии 5 метров от точечного источника составляет 20 мВт/м 2 . Найти плотность потока электромагнитного излучения на расстоянии 10 метров от этого источника.
Расстояние по условию задачи увеличилось вдвое. Так как плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника, при увеличении расстояния вдвое интенсивность излучения уменьшится в 4 раза. То есть, она станет равной 5 мВт/м 2 .
Зависимость плотности потока излучения от частоты
Напряженность электрического поля и магнитная индукция электромагнитной волны пропорциональны ускорению заряда. Ускорение при гармонических колебаниях пропорционально квадрату частоты. Поэтому напряженность электрического поля и магнитная индукция также пропорциональны квадрату частоты:
Плотность энергии электрического поля пропорциональна квадрату напряженности поля. Энергия магнитного поля, как это можно показать, пропорциональна квадрату магнитной индукции. Полная плотность энергии электромагнитного поля равна сумме плотностей энергий электрического и магнитного полей. Поэтому плотность потока излучения I пропорциональна:
Плотность потока излучения пропорциональна четвертой степени частоты. Так, при увеличении частоты колебаний зарядов в 2 раза энергия, излучаемая ими, возрастает в 16 раз. При увеличении частоты в 3 раза, энергия излучения увеличивается в 81 раз, и т.д.
Пример №3. Частота электромагнитной волны уменьшилась в 4 раза. Найти, во сколько раз изменилась плотность потока излучения.
Так как плотность потока излучения пропорциональна четвертой степени частоты, мы можем найти плотность потока излучения путем извлечения
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
4 √ 4 = √ √ 4 = √ 2 ≈ 1 , 4
Плотность потока излучения уменьшилась в 1,4 раза.
Видео:ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ. ЧТО ЭТО? [Радиолюбитель TV 6]Скачать
![ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ. ЧТО ЭТО? [Радиолюбитель TV 6]](https://i.ytimg.com/vi/kbkhg3BeOUI/0.jpg)
Свойства электромагнитных волн
Современные радиотехнические устройства позволяют провести очень наглядные опыты по наблюдению свойств электромагнитных волн. При этом лучше всего пользоваться волнами сантиметрового диапазона. Эти волны излучаются специальным генератором сверхвысокой частоты (СВЧ). Электрические колебания генератора модулируют звуковой частотой. Принятый сигнал после детектирования подается на громкоговоритель.
| Свойство 1 — Поглощение электромагнитных волн | |
 | Если расположить рупоры друг против друга и добиться хорошей слышимости звука в громкоговорители, а затем поместить между ними диэлектрик, звук будет менее громким. |
| Свойство 2 — Отражение электромагнитных волн | |
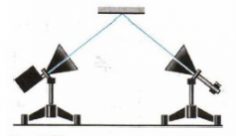 | Если диэлектрик заменить металлической пластиной, то звук перестанет быть слышимым. Волны не достигают приемника вследствие отражения. Отражение происходит под углом, равным углу падения, как и в случае световых и механических волн. Чтобы убедиться в этом, рупоры располагают под одинаковыми углами к большому металлическому листу. Звук исчезнет, если убрать Лист — наружный орган растения, основными функциями которого является фотосинтез, газообмен и транспирация. » data-gt-translate-attributes='[]’>лист или повернуть его. |
| Свойство 3 — Преломление электромагнитных волн | |
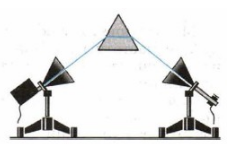 | Электромагнитные волны изменяют свое направление (преломляются) на границе диэлектрика. Это можно обнаружить с помощью большой треугольной призмы из парафина. Рупоры располагают под углом друг к другу, как и при демонстрации отражения. Металлический лист заменяют затем призмой. Убирая призму или поворачивая ее, наблюдают исчезновение звука. |
| Свойство 4 — Поперечность электромагнитных волн | |
 | Поместим между генератором и приемником решетку из параллельных металлических стержней. Решетку расположим так, чтобы стержни были горизонтальными или вертикальными. При одном из этих положений, когда электрический вектор параллелен стержням, в них возбуждаются токи, в результате чего решетка начинает отражать волны, подобно сплошной металлической пластине. Когда же вектор перпендикулярен стержням, токи в них не возбуждаются и электромагнитная волна проходит через решетку. |
Видео:Раскрытие тайн электромагнитной волныСкачать

Шкала электромагнитных волн
Электромагнитные волны имеют большое разнообразие. Они классифицируются по длине волны λ или связанной с ней частоте ν. Шкала электромагнитных волн включает в себя:
- радиоволны;
- оптическое излучение;
- ионизирующее излучение.
Укажем частоты и длины указанных волн, а также их подробную классификацию в таблице.
| Наименование диапазона волн | Длины волн (м) | Частоты (Гц) |
| Радиоволны | ||
| Инфразвук, звук | >10 5 | 3 |
| Сверхдлинные волны (СДВ) | 10 4 –10 5 | 3∙10 3 –3∙10 4 |
| Длинные волны (ДВ) | 10 3 –10 4 | 3∙10 4 –3∙10 5 |
| Средние волны (СВ) | 10 2 –10 3 | 3∙10 5 –3∙10 6 |
| Короткие волны (КВ) | 10–100 | 3∙10 6 –3∙10 7 |
Ультракороткие (УКВ):
|
|
|
| Оптические волны | ||
| Инфракрасное излучение | 0,78∙10 –6 –10 –4 | 3∙10 11 –4∙10 14 |
| Видимый свет | 0,38∙10 –6 –0,78∙10 –6 | 4∙10 14 –7,5∙10 14 |
| Ультрафиолетовое излучение | 10 –7 –0,38∙10 –6 | 7,5∙10 11 –3∙10 15 |
| Ионизирующее излучение | ||
| Рентгеновское излучение | 5∙10 –12 –10 –8 | 3∙10 16 –6∙10 19 |
| Гамма-излучение | –12 | >6∙10 19 |
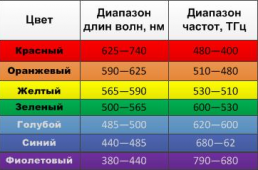
Частоты и длины волн электромагнитного излучения видимого спектра смотрите на рисунке ниже.
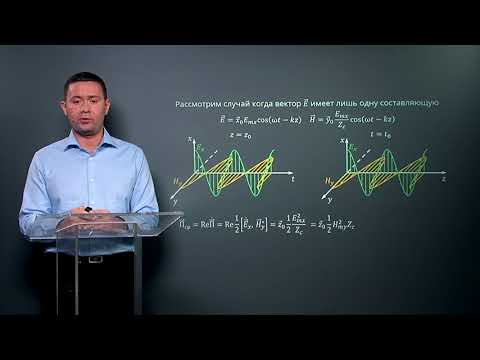
В электромагнитной волне, распространяющейся со скоростью → v , происходят колебания векторов напряжённости электрического поля → E и индукции магнитного поля → B . При этих колебаниях векторы → v , → E , → B . имеют взаимную ориентацию:
Видео:Электромагнитные волны в 4K (Ultra HD) 60 FPS. Как выглядит электромагнитная волнаСкачать
2.6. Электромагнитные волны
Любой колебательный контур излучает энергию. Изменяющееся электрическое поле возбуждает в окружающем пространстве переменное магнитное поле, и наоборот. Математические уравнения, описывающие связь магнитного и электрического полей, были выведены Максвеллом и носят его имя. Запишем уравнения Максвелла в дифференциальной форме для случая, когда отсутствуют электрические заряды (
Величины 

Постоянные 

В отсутствие зарядов и токов невозможно существование статических электрического и магнитного полей. Однако переменное электрическое поле возбуждает магнитное поле, и наоборот, переменное магнитное поле создает электрическое поле. Поэтому имеются решения уравнений Максвелла в вакууме, в отсутствие зарядов и токов, где электрические и магнитные поля оказываются неразрывно связанными друг с другом. В теории Максвелла впервые были объединены два фундаментальных взаимодействия, ранее считавшихся независимыми. Поэтому мы говорим теперь об электромагнитном поле.
Колебательный процесс в контуре сопровождается изменением окружающего его поля. Изменения, происходящие в окружающем пространстве, распространяются от точки к точке с определенной скоростью, то есть колебательный контур излучает в окружающее его пространство энергию электромагнитного поля.
Электромагнитная волна — это распространяющееся в пространстве электромагнитное поле, в котором напряженность электрического и индукция магнитного полей изменяются по периодическому закону.
При строго гармоническом изменении во времени векторов 

Получим из уравнений Максвелла волновые уравнения для векторов 

Волновое уравнение для электромагнитных волн
Как уже отмечалось в предыдущей части курса, ротор (rot) и дивергенция (div) — это некоторые операции дифференцирования, производимые по определенным правилам над векторами. Ниже мы познакомимся с ними поближе.
Возьмем ротор от обеих частей уравнения
При этом воспользуемся доказываемой в курсе математики формулой:
где 
Получаем в итоге:
Выразим rotB через электрическое поле с помощью уравнения Максвелла:
и используем это выражение в правой части (2.93). В результате приходим к уравнению:
и вводя показатель преломления среды
запишем уравнение для вектора напряженности электрического поля в виде:
Сравнивая с (2.69), убеждаемся, что мы получили волновое уравнение, где v — фазовая скорость света в среде:
Взяв ротор от обеих частей уравнения Максвелла
и действуя аналогичным образом, придем к волновому уравнению для магнитного поля:
Полученные волновые уравнения для 

В отсутствие среды (при 
Основные свойства электромагнитных волн
Рассмотрим плоскую монохроматическую электромагнитную волну, распространяющуюся вдоль оси х:
Возможность существования таких решений следует из полученных волновых уравнений. Однако напряженности электрического и магнитного полей не являются независимыми друг от друга. Связь между ними можно установить, подставляя решения (2.99) в уравнения Максвелла. Дифференциальную операцию rot, применяемую к некоторому векторному полю А можно символически записать как детерминант:
Подставляя сюда выражения (2.99), зависящие только от координаты x, находим:
Дифференцирование плоских волн по времени дает:
Тогда из уравнений Максвелла следует:
Отсюда следует, во-первых, что электрическое и магнитное поля колеблются в фазе:
Далее, ни у 

Иными словами и в изотропной среде,
электромагнитные волны поперечны: колебания векторов электрического и магнитного полей происходят в плоскости, ортогональной направлению распространения волны.
Тогда можно выбрать координатные оси так, чтобы вектор 
Рис. 2.27. Колебания электрического и магнитного полей в плоской электромагнитной волне
В этом случае уравнения (2.103) приобретают вид:
Отсюда следует, что вектор 
Иначе говоря, векторы электрического и магнитного поля ортогональны друг другу и оба — направлению распространения волны. С учетом этого факта уравнения (2.104) еще более упрощаются:
Отсюда вытекает обычная связь волнового вектора, частоты и скорости:
а также связь амплитуд колебаний полей:
Отметим, что связь (2.107) имеет место не только для максимальных значений (амплитуд) модулей векторов напряженности электрического и магнитного поля волны, но и для текущих — в любой момент времени.
Итак, из уравнений Максвелла следует, что электромагнитные волны распространяются в вакууме со скоростью света. В свое время этот вывод произвел огромное впечатление. Стало ясно, что не только электричество и магнетизм являются разными проявлениями одного и того же взаимодействия. Все световые явления, оптика, также стали предметом теории электромагнетизма. Различия в восприятии человеком электромагнитных волн связаны с их частотой или длиной волны.
Шкала электромагнитных волн представляет собой непрерывную последовательность частот (и длин волн) электромагнитного излучения. Теория электромагнитных волн Максвелла позволяет установить, что в природе существуют электромагнитные волны различных длин, образованные различными вибраторами (источниками). В зависимости от способов получения электромагнитных волн их разделяют на несколько диапазонов частот (или длин волн).
На рис. 2.28 представлена шкала электромагнитных волн.
Рис. 2.28. Шкала электромагнитных волн
Видно, что диапазоны волн различных типов перекрывают друг друга. Следовательно, волны таких длин можно получить различными способами. Принципиальных различий между ними нет, поскольку все они являются электромагнитными волнами, порожденными колеблющимися заряженными частицами.
Уравнения Максвелла приводят также к выводу о поперечности электромагнитных волн в вакууме (и в изотропной среде): векторы напряженности электрического и магнитного полей ортогональны друг другу и направлению распространения волны.
http://www.femto.com.ua/articles/part_1/0560.html – Волновое уравнение. Материал из Физической Энциклопедии.
http://elementy.ru/trefil/24 – Уравнения Максвелла. Материал из «Элементов».
http://telecomclub.org/?q=node/1750 – Уравнения Максвелла и их физический смысл.
http://principact.ru/content/view/188/115/ – Кратко об уравнениях максвелла для электромагнитного поля.
Эффект Доплера для электромагнитных волн
Пусть в некоторой инерциальной системе отсчета К распространяется плоская электромагнитная волна. Фаза волны имеет вид:
Наблюдатель в другой инерциальной системе отсчета К’, движущейся относительно первой со скоростью V вдоль оси x, также наблюдает эту волну, но пользуется другими координатами и временем: t’, r’. Связь между системами отсчета дается преобразованиями Лоренца:
Подставим эти выражения в выражение для фазы 

Это выражение можно записать как
где 

Для электромагнитной волны в вакууме
Пусть направление распространения волны составляет в первой системе отсчета угол 
Тогда выражение для частоты волны в движущейся системе отсчета принимает вид:
Это и есть формула Доплера для электромагнитных волн.
Если 
Если 
При скоростях V 2 (солнечная постоянная). Найдем среднюю амплитуду колебаний E0 вектора электрической напряженности в солнечном излучении. Вычислим амплитуды колебаний напряженности магнитного поля H0 и вектора магнитной индукции B0 в волне.
Ответ находим сразу из уравнений (3.127), где полагаем 
Электромагнитные волны поглощаются и отражаются телами, следовательно, они должны оказывать на тела давление. Рассмотрим плоскую электромагнитную волну, падающую нормально на плоскую проводящую поверхность. В этом случае электрическое поле волны возбуждает в теле ток, пропорциональный Е. Магнитное поле волны по закону Ампера будет действовать на ток с силой, направление которой совпадает с направлением распространения волны. В 1899 г. в исключительно тонких экспериментах П.И. Лебедев доказал существование светового давления. Можно показать, что волна, несущая энергию W, обладает и импульсом:
Пусть электромагнитная волна падает в вакууме по нормали на площадь А и полностью поглощается ею. Предположим, что за время 

На площадку действует со стороны волны сила
Давление Р, оказываемое волной, равно
Если средняя плотность энергии в волне равна , то на площадь А за время 

Отсюда находим давление электромагнитной волны (света):
Если площадка идеально отражает всю падающую на нее энергию, то давление будет в два раза большим, что объясняется очень просто: одинаковый вклад в давление в этом случае дают как падающая, так и отраженная волны, в случае полностью поглощающей поверхности отраженной волны просто нет.
Пример 3. Найдем давление Р солнечного света на Землю. Используем значение солнечной постоянной из предыдущего примера. Искомое давление равно:
Пример 4. Найдем давление Р лазерного пучка на поглощающую мишень. Выходная мощность лазера N = 4.6 Вт, диаметр пучка d = 2.6 мм.
Видео:Физика 11 класс (Урок№10 - Электромагнитные волны.)Скачать

Уравнения электромагнитной волны
Электромагнитные волны представляют собой переменное электромагнитное поле, распространяющееся в пространстве.
Электромагнитные волны являются поперечными: векторы и сильных электрических и магнитных полей волны взаимно перпендикулярны и лежат в плоскости и лежат в плоскости, перпендикулярной вектору волны скорость распространения. Векторы и образуют правую систему.
Электромагнитные волновые уравнения
Связь между векторами и в электромагнитной волне, распространяющейся в непроводящей среде, определяется уравнениями Максвелла, в которых (плотность заряда) и (вектор плотности тока) считаются равными нулю:
где — напряженность электрического поля, — вектор магнитной индукции, — вектор магнитной интенсивности, — вектор электрического смещения.
Таким образом, система уравнений (1) является уравнениями электромагнитной волны в непроводящей среде.
В случае однородной, изотропной, непроводящей среды, не обладающей ферромагнитными или сегнетоэлектрическими свойствами, уравнение электромагнитной волны будет иметь вид:
где — электрические и магнитные постоянные, — относительная электрическая и магнитная проницаемость среды.
Векторы и поля электромагнитной волны могут быть выражены через скалярные и векторные потенциалы. Тогда уравнения электромагнитной волны будут выглядеть так:
где — оператор Лапласа,
Каждая из проекций векторов на ось прямоугольной декартовой системы координат и удовлетворяет волновому уравнению (4):
где — фазовая скорость электромагнитной волны, .В вакууме . Для всех сред, кроме ферромагнитных, и
Определение и уравнение плоской электромагнитной волны
Электромагнитная волна называется плоскостью, если векторы и зависят только от времени и одной декартовой координаты.
Для плоской электромагнитной волны, распространяющейся вдоль положительного направления оси Ox правой системы координат, уравнения электромагнитной волны записываются следующим образом:
где — единичный вектор, проведенный в направлении распространения волны. Мы видим, что плоскую электромагнитную волну можно полностью определить, используя только векторный потенциал . В вакууме:
Определение и уравнение монохроматической электромагнитной волны
Электромагнитная волна называется монохроматической, если компоненты вектора электромагнитного поля и
создают гармонические колебания одной и той же частоты, называемые частотой волн. Произвольная немонохроматическая волна может быть представлена как набор монохроматических волн.
Силы электрического и магнитного полей плоской монохроматической волны часто представлены в виде:
где — волновое число.
Очевидно, что комплексные функции эквивалентны (8)
Здесь k — волновой вектор, а его модуль равен значению
Электрическое и магнитное поля плоской волны перпендикулярны друг другу.
Примеры решения проблем
Найти средний вектор Пойнтинга для плоской электромагнитной волны , если волна распространяется в вакууме.
Решение По определению вектор Пойнтинга:
Запишем средний вектор Пойнтинга, так как
Для плоской электромагнитной волны положим:
Запишем уравнение полосой электромагнитной волны:
Дифференцируем (1.3) на x:
Дифференцируя (1.4) с t, получаем:
Подставим (1.7) и (1.8) в (1.5), получим:
Подставим (1.10) в (1.1), то в (1.2) получим:
Поскольку волна распространяется в вакууме, мы пишем:
Средний вектор вектора Посвящения для плоской электромагнитной волны:
Плоская электромагнитная волна из первой среды падает на границу под определенным углом , частично проникает во вторую среду и отражается от границы раздела между двумя средами. Граф .
1) Определите, как изменяется частота электромагнитной волны во время отражения и преломления.
2) Докажите, что лучи, падающие, отраженные и преломленные, лежат в одной плоскости.
3) Найти законы отражения и преломления электромагнитной волны.
4) Определить формулу для связи амплитудных значений векторов поля (для отражения и преломления электромагнитных волн (для нормального падения).
Используя уравнение для интенсивности электромагнитной волны из системы уравнений (9), запишем векторы интенсивности падающего , отраженного и преломленного волн:
Необходимо найти связь между амплитудами, частотами колебаний и волновыми векторами падающей , отраженной и преломленной (92) волн. Мы используем непрерывность тангенциальной составляющей поля на границе раздела между двумя средами:
Проанализируем равенство (2.4) с учетом (2.1), (2.2), (2.3) в следующем порядке:
1) Исправьте некоторую точку на интерфейсе, выберите одну временную зависимость в равенстве (2.4), написанную в проекции на некоторую ось:
Это равенство должно выполняться тождественно для всех значений t, что возможно только в том случае, если: (2.6). Мы получаем: частота при отражении и преломлении не изменяется.
2) Разделив равенство (2.4) на общий коэффициент времени, получим выражение вида:
Равенство (2.6) должно выполняться для всех точек интерфейса, что возможно только при условии:
Пусть то и , откуда следует, что векторы лежат в одной плоскости.
3) Плоскость векторов совпадает с плоскостью Oxz (рис.1). Выберите начало вектора на оси Ox. Из формулы (2.7) следует:
Используя формулу, связывающую волновой вектор с частотой , получим:
Отсюда мы получаем законы отражения (2.10) и преломления (2.11):
является показателем преломления.
4) Пусть волна падает перпендикулярно поверхности раздела (рис. 2), причем вектор направлен по оси Ox. (Тогда вектор направлен по оси Oy.)
Используя уравнения для плоской электромагнитной волны, запишем:
Эти формулы определяют поле падающей волны. Для отраженной волны, распространяющейся в обратном направлении имеем:
Преломленная волна запишется в виде:
Исходя из непрерывности тангенциальной составляющей вектора и тангенциальной составляющей вектора на плоскости z=0 к уравнениям:
Решая систему находим:
Ответ 1) Частота при отражении и преломлении не изменяются.
2) Доказано, что волновые векторы лежат в одной плоскости, следовательно, лучи падающий отраженный и преломленный лежат в одной плоскости.
3) Получены законы
4) Формулы (2.12) есть формулы связи амплитудных значений векторов поля при отражении и преломлении электромагнитных волн (при нормальном падении).
💥 Видео
Электромагнитные волныСкачать

Билет №34 "Электромагнитные волны"Скачать

Электромагнитные волны НАГЛЯДНО. ТВ урок.Скачать

Электромагнитные волны | Физика 9 класс #44 | ИнфоурокСкачать

Парадокс электромагнитной волныСкачать

Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Поляризация плоской электромагнитной волныСкачать
Электромагнитные волны. 11 класс.Скачать

4.8 Плотность потока мощности электромагнитной волныСкачать

4.3 Плоские электромагнитные волны в идеальных диэлектрических средахСкачать
Урок 384. Излучение электромагнитных волн.Скачать