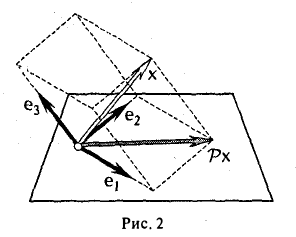
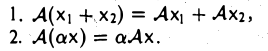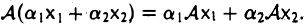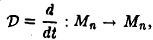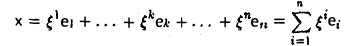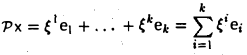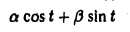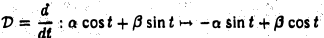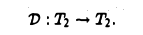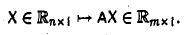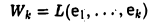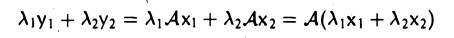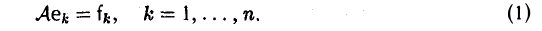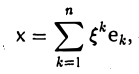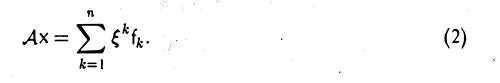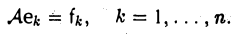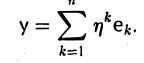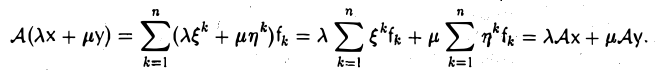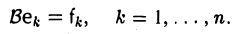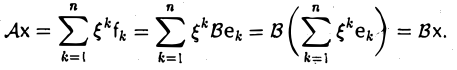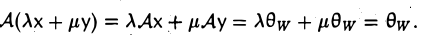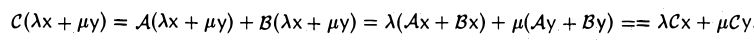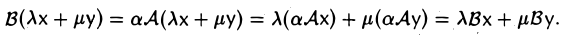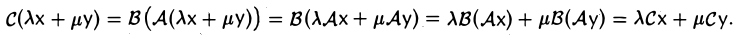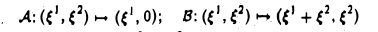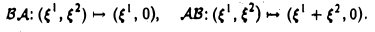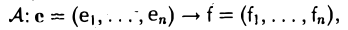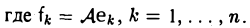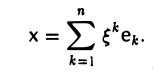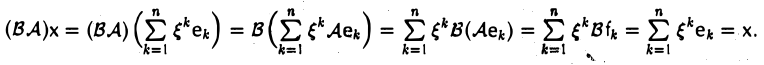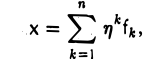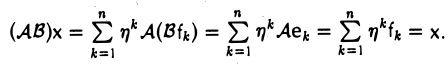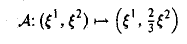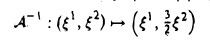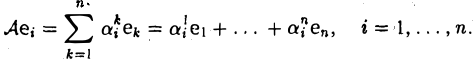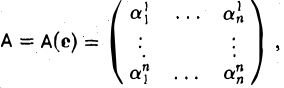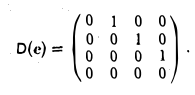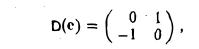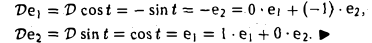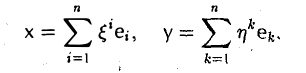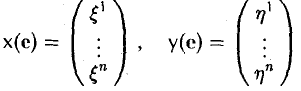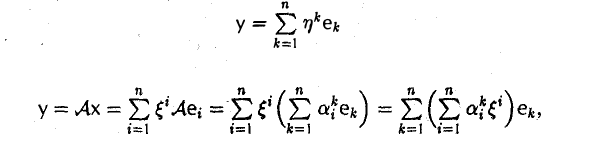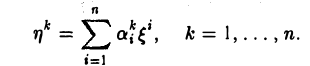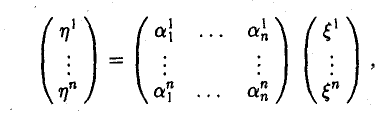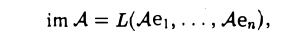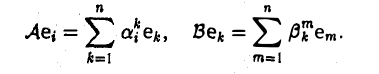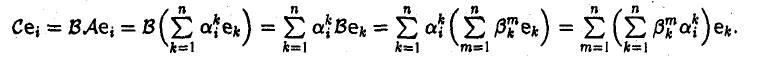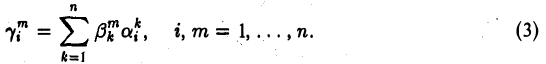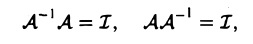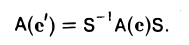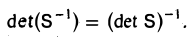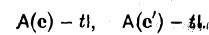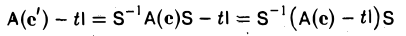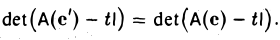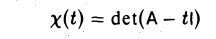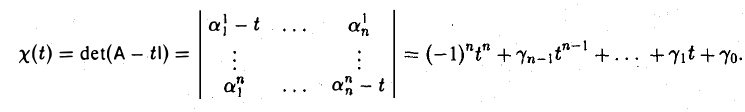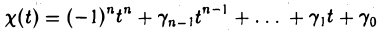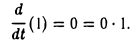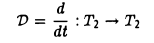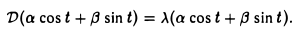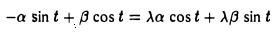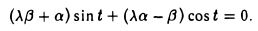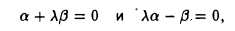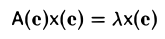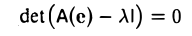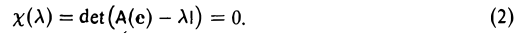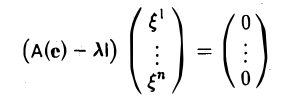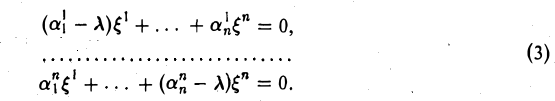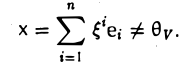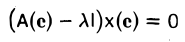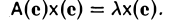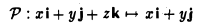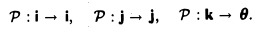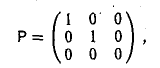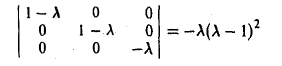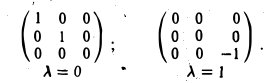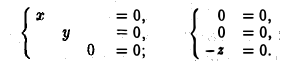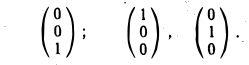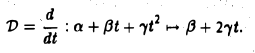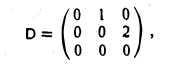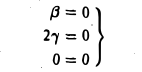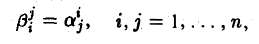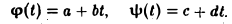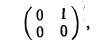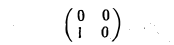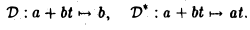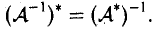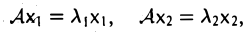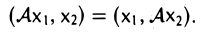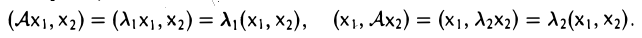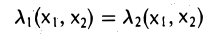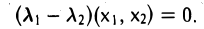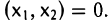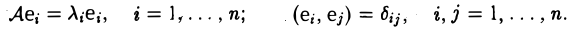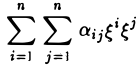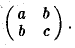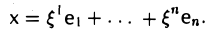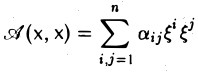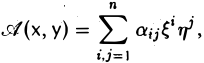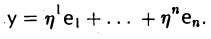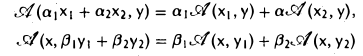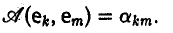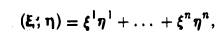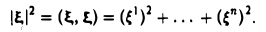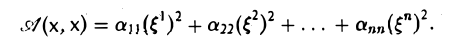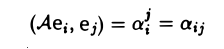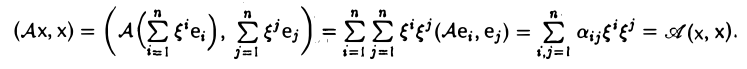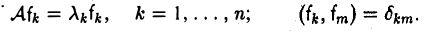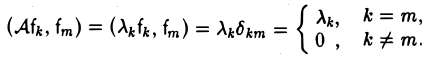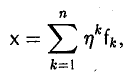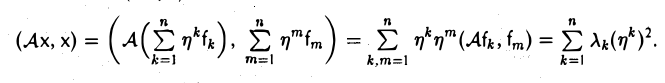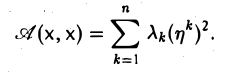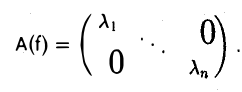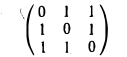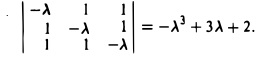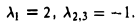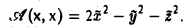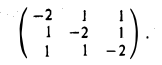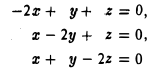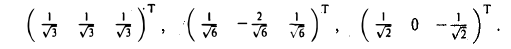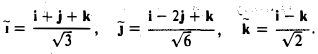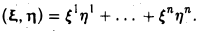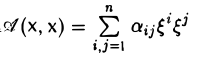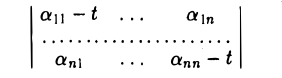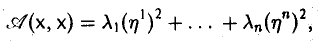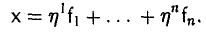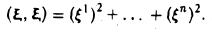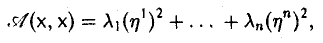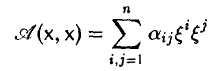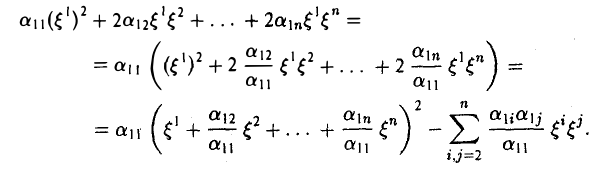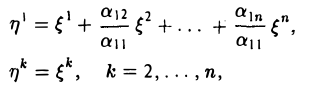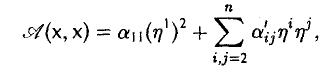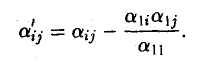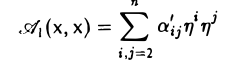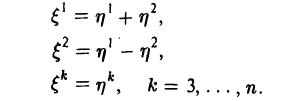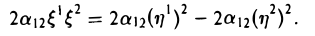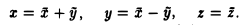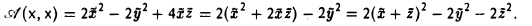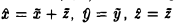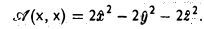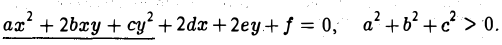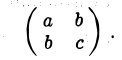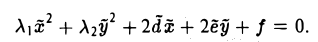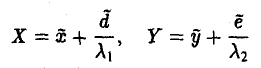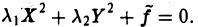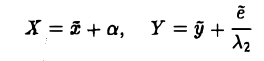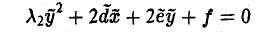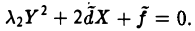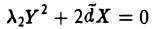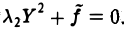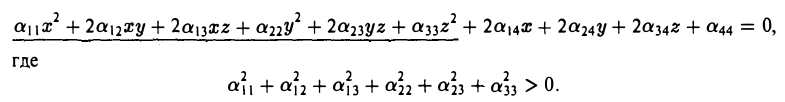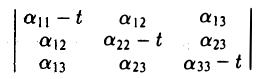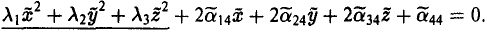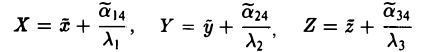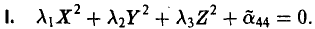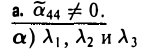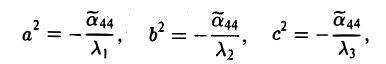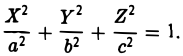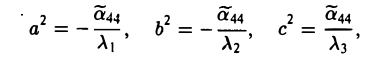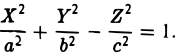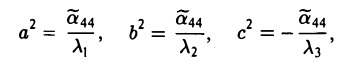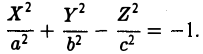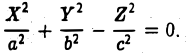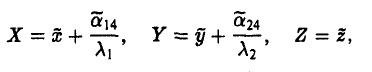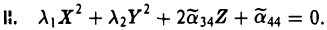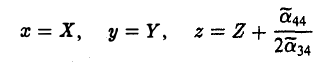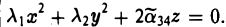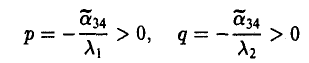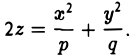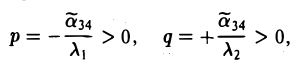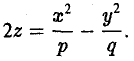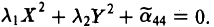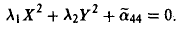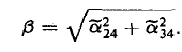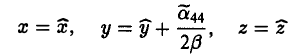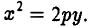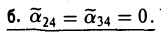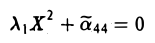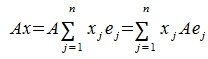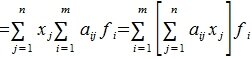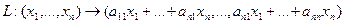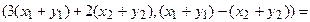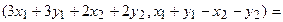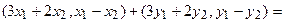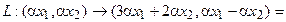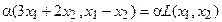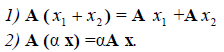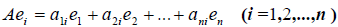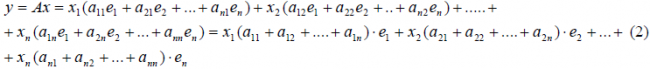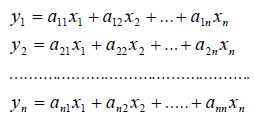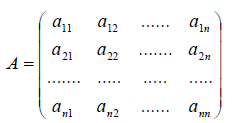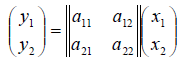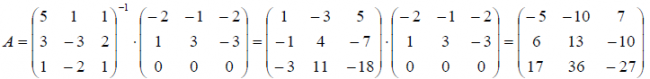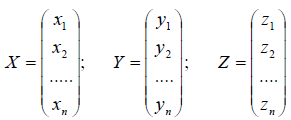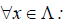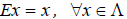Ядром линейного отображения называется множество таких векторов , что , т.е. множество векторов из , которые отображаются в нулевой вектор пространства . Ядро отображения обозначается:
Образом линейного отображения называется множество образов всех векторов из . Образ отображения обозначается или
Заметим, что символ следует отличать от — мнимой части комплексного числа.
- Примеры ядер и образов линейных отображений
- Свойства ядра и образа линейного отображения
- Образ базисного вектора это
- Линейное отображение с примерами решения и образцами выполнения
- Определение линейного отображения. Образ и ядро линейного отображения
- Примеры линейных отображений
- Матрица линейного оператора
- Собственные значения и собственные элементы
- Достаточность. Способ построения собственного элемента
- Сопряженный оператор
- Свойства операции сопряжения
- Симметричный оператор
- Свойства симметричного оператора
- Свойства положительного оператора
- Квадратичные формы
- Критерий Сильвестра (знакоположительное квадратичной формы)
- Метод Лагранжа
- Классификация кривых и поверхностей второго порядка
- Кривые
- Поверхности
- Дополнение к линейным отображениям
- Линейные операторы
- 1. Понятие линейного оператора
- 2. Сложение линейных операторов
- 3. Умножение линейных операторов
- 4. Умножение линейного оператора на число
- 5. Нулевой оператор
- 6. Противоположный оператор
- 7. Ядро линейного оператора
- 8. Образ линейного оператора
- 9. Ранг линейного оператора
- Матрица линейного оператора примеры
- Построение матрицы по заданной формуле отображения.
- Матрица линейного оператора
- Примеры линейных операторов
- Действия над операторами
- 1. Понятие линейного оператора
- 2. Сложение линейных операторов
- 3. Умножение линейных операторов
- 4. Умножение линейного оператора на число
- 5. Нулевой оператор
- 6. Противоположный оператор
- 7. Ядро линейного оператора
- 8. Образ линейного оператора
- 9. Ранг линейного оператора
- Линейное отображение с примерами решения и образцами выполнения
- Определение линейного отображения. Образ и ядро линейного отображения
- Примеры линейных отображений
- Матрица линейного оператора
- Собственные значения и собственные элементы
- Достаточность. Способ построения собственного элемента
- Сопряженный оператор
- Свойства операции сопряжения
- Симметричный оператор
- Свойства симметричного оператора
- Свойства положительного оператора
- Квадратичные формы
- Критерий Сильвестра (знакоположительное квадратичной формы)
- Метод Лагранжа
- Классификация кривых и поверхностей второго порядка
- Кривые
- Поверхности
- Дополнение к линейным отображениям
Видео:Ядро и образ линейного оператораСкачать

Примеры ядер и образов линейных отображений
1. Ядром нулевого отображения является все пространство , а образом служит один нулевой вектор, т.е.
2. Рассмотрим отображение , которое ставит в соответствие каждому вектору n-мерного линейного пространства его координатный столбец относительно заданного базиса . Ядром этого отображения является нулевой вектор пространства , поскольку только этот вектор имеет нулевой координатный столбец . Образ преобразования совпадает со всем пространством , так как это преобразование сюръективно (любой столбец из является координатным столбцом некоторого вектора пространства ).
3. Рассмотрим отображение , которое каждому вектору n-мерного евклидова пространства ставит в соответствие алгебраическое значение его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение — множество векторов, ортогональных . Образом является все множество действительных чисел .
4. Рассмотрим отображение , которое каждому многочлену степени не выше ставит в соответствие его производную. Ядром этого отображения является множество многочленов нулевой степени, а образом — все пространство .
Видео:Как разложить вектор по базису - bezbotvyСкачать

Свойства ядра и образа линейного отображения
1. Ядро любого линейного отображения является подпространством: .
В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что
т.е. нулевой вектор отображается в нулевой вектор . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:
Следовательно, множество является линейным подпространством пространства .
2. Образ любого линейного отображения является подпространством: .
В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если , то существует вектор такой, что . Тогда , то есть .
Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.
Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа: .
3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).
В самом деле, если любой базис пространства , то . Поэтому максимальное число линейно независимых векторов системы (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы отображения, т.е. рангу матрицы: .
4. Линейное отображение инъективно тогда и только тогда, когда , другими словами, когда дефект отображения равен нулю: .
Действительно, образом нулевого вектора служит нулевой вектор . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор , иначе два разных вектора имели бы один и тот же образ . Обратно, при условии разные векторы не могут иметь одинаковые образы , так как в этом случае из равенств , следует, что ненулевой вектор (приходим к противоречию).
5. Линейное отображение сюръективно тогда и только тогда, когда , другими словами, когда ранг отображения равен размерности пространства образов: .
6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда и одновременно.
Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:
Действительно, пусть . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства . Покажем, что векторы образуют базис подпространства .
Во-первых, , так как образ любого вектора линейно выражается через векторы
Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:
то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению . Учитывая, что , заключаем: . Получили разложение нулевого вектора по линейно независимой системе векторов, значит, все коэффициенты . Поэтому равенство справедливо только для тривиальной линейной комбинации, т.е. система векторов линейно независимая.
Таким образом, векторы образуют базис подпространства , а его размерность определяется количеством базисных векторов, т.е. , что равносильно (9.3).
Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).
Действительно, для обратимости преобразования (см. свойство 6) его матрица (размеров ) должна удовлетворять условиям (см. свойства 3,4,5):
Тогда по теореме 9.1 заключаем, что , т.е. матрица — квадратная n-го порядка и невырожденная , что и требовалось доказать.
Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).
Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Образ базисного вектора это
Видео:10.2 Матрица линейного оператораСкачать

Линейное отображение с примерами решения и образцами выполнения
Линейное отображение — обобщение линейной числовой функции, а точнее, функции на случай более общего множества аргументов и значений. Линейные отображения, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Определение линейного отображения. Образ и ядро линейного отображения
Пусть V и W — линейные пространства (либо оба вещественные, либо оба комплексные). Линейным отображением линейного пространства V в линейное пространство W называется правило А, согласно которому каждому элементу х из пространства V ставится в соответствие (единственный) элемент у = Ах из пространства W так, что
Эти два требования можно объединить в одно:
Обозначение: A:V → W.
Примеры линейных отображений
- Пусть V = W = Мп, где Мп — пространство многочленов, степень которых не выше п. Правило
согласно которому каждому многочлену из Мп ставится в соответствие его производная, является линейным отображением (производная суммы равна сумме производных, постоянный сомножитель можно выносить из-под знака производной).
2. Правило, по которому каждому элементу х из V ставится в соответствие элемент λх из V ( λ ≠ 0 и фиксировано), — преобразование подобия — является линейным отображением (рис. 1).
3. Пусть у = (еi…, еn) — базис пространства V. Поставим произвольному элементу
в соответствие элемент
(здесь k
4. Cовокупность Т2 тригонометрических многочленов вида
образует линейное пространство. Правило
является линейным отображением
5. Пусть 
Образом линейного отображения А: V → W называется множество im А всех элементов из пространства W, обладающих следующим свойством элемент у лежит в im А, если в пространстве V найдется элемент х, такой, что Ах = у. Примеры.
1′. Образом операции дифференцирования V : Мn — Мп является совокупность многочленов, степень которых не выше п — 1,
2′. Образ отображения подобия совпадает со всем пространством V.
3′. Образ отображения проектирования V : V → V является подпространством
4′. Образ операции дифференцирования V : T2 → Т2 совпадает со всем пространством Т2
Теорема:
Образ im А линейного отображения А: V → W является линейным подпространством пространства W.
Пусть у1 и у2 — элементы из im А. Это означает, что в пространстве V найдутся элементы x1 и х2, такие, что -Ax1 = y1 и Ах2 = у2. Из формулы
вытекает, что произвольная линейная комбинация элементов y1 и у2 также лежит в im А.
Размерность образа линейного отображения называется рангом этого линейного отображения.
Обозначение: rang А.
Определение:
Линейные отображения А: V → W и В: V W называются равными, если для любого элемента х из пространства V выполняется равенство Ах = Вх.
Обозначение: А = В.
Теорема:
Построение линейного отображения. Пусть V и W — линейные пространства, e = (e1… , еn) — базис пространства V, a f1. . ., fn — произвольные элементы из пространства W. Тогда существует и притом ровно одно линейное отображение
A :V → W,
А. Существование. Разложим произвольный элемент х из пространства V по базису с этого пространства,
и построим отображение А: V → W по следующему правилу:
В линейности отображения А убедимся непосредственно. Пусть
Тогда согласно правилу (2)
Б. Единственность. Покажем, что требованием (1) линейное отображение А определяется однозначно.
Пусть В: V → W — линейное отображение и
Вычисляя действия А и В на произвольный элемент х из V, убеждаемся в том, что в обоих случаях результат один и тот же —
Значит, отображения A и В совпадают.
Таким образом, линейное отображение можно задать его действием только на элементы базиса.
Ядром линейного отображения А: V → W называется множество ker А всех элементов из пространства V, каждый из которых отображение А переводит в нулевой элемент θw пространства W.
Примеры:
1″. Многочлены нулевой степени образуют ядро операции дифференцирования V: Мп -> Мп.
2″. Ядро отображения подобия состоит из нулевого элемента θv пространства V.
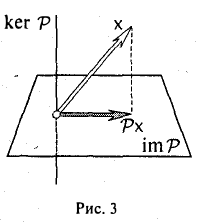
3″. Ядром отображения проектирования P: V→V является линейное подпространство L(ek+1,…, еn) (рис. 3).
4″. Ядро операции дифференцирования D:T2→Т2 состоит из нуля.
5″. Ядром отображения
является множество решений однородной линейной системы
АХ = 0.
Теорема:
Ядро линейного отображения А: V
→W является линейным подпространством пространства V.
Из равенств Ах = θw и Ay = θw вытекает, что
Размерность ядра линейного отображения называется дефектом этого отображения.
Обозначение: defect . Операции над линейными отображениям
Пусть V и W — линейные пространства и A:V W, B:V→W — линейные отображения. Суммой линейных отображений А и В называется отображение С: V→W, определяемое п о следующему правилу:
Сх = Ах + Вх
для любого элемента х из V. Нетрудно убедиться в том, что отображение С является линейным. В самом деле,
Обозначение: С = А + В.
Произведением линейного отображения A:V→W на число а называется отображение В: V —> W, определяемое по правилу:
Вх = аАх
для любого элемента х из V. Отображение В линейно:
Обозначение: В = а А.
В дальнейшем мы ограничимся рассмотрением линейных операторов — линейных отображений, действующих из пространства V в это же пространство V. Среди рассмотренных выше примеров отображений линейными операторами являются дифференцирование, подобие и проектирование; умножение столбца на квадратную матрицу также является линейным оператором.
Оператор I: V —> V, задаваемый правилом Ix = х для любого элемента х из V, называется тождественным.
Введем операцию умножения линейных операторов. Пусть А: V → V и В: V→V — линейные операторы. Произведением оператора А на оператор В называется отображение С: V → V, определяемое по правилу
Сх = В(Ах),
где х — произвольный элемент из V. Покажем, что С — линейный оператор:
Обозначение: С = В А.
Замечание:
Порядок сомножителей в произведении линейных операторов является существенным, как показывает следующий пример.
Пример:
Пусть V = R 2 . Отображения
— линейные операторы, действующие из R 2 в R 2 (рис. 4). Тогда
Пусть A: V → V — линейный оператор. Линейный оператор В: V → V называется обратным оператору А, если выполнены следующие равенства
ВА = АВ= I,
где I: V —> V — тождественный оператор.
Теорема:
Для того, чтобы у линейного оператора А: V → V был обратный, необходимо и достаточно, чтобы образ оператора А совпадал со всем пространством,
im А = V.
Предположим сначала, что обратный оператор В у заданного оператора А существует и покажем, что произвольно взятый элемент у из пространства V непременно лежит в im А. Подействовав оператором А на элемент х = В у, согласно определению (1), получим
Ах = А(Ву) = (АВ)у = Iу — у.
Значит, элемент у является образом элемента х = By и, следовательно, лежит в im А. Тем самым imA = V.
Пусть теперь образ оператора А совпадает со всем пространством V:
imA = V.
rang А = dim V.
Поэтому оператор А переводит базис пространства V снова в базис:
Построим линейный оператор В по следующему правилу
Согласно теореме 1, условием (2) оператор В определяется однозначно.
Пусть х — произвольный элемент пространства V. Вычислим (ВA)х и (АВ)х. Разложим х по базису с. Имеем
Подействовав на него оператором В А, с учетом формул (2) получаем, что
Аналогично, раскладывая элемент х по базису f,
и действуя на него оператором АВ, имеем
ВAх = х, АВх = х
для любого элемента х из V и, значит,
В А = АВ = I.
Замечание:
В ходе доказательства этой теоремы мы установили также, что обратный к А оператор В определен однозначно.
Для оператора, обратного к А, принято следующее обозначение: А -1 .
Следствие:
Линейный оператор А: V → V обратим (имеет обратный) тогда и только тогда, когда его ядро тривиально,
ker А= .
Справедливость этого утверждения вытекает из теоремы 3 и формулы.
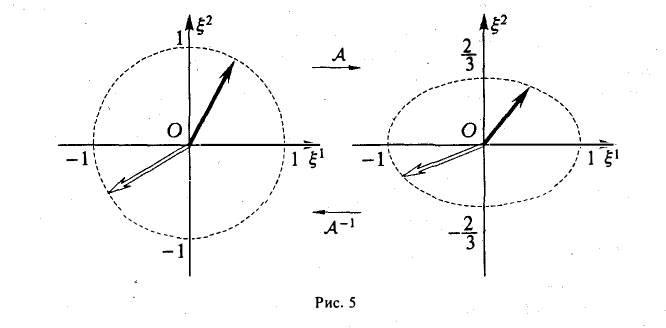
Пример:
осуществляет равномерное сжатие плоскости к оси ξ 1 (с коэффициентом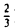
— равномерное растяжение (с коэффициентом 3/2) (рис. 5).
Матрица линейного оператора
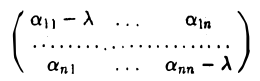
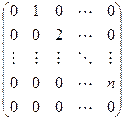
Пусть линейный оператор А: V —> V преобразует элементы базиса e = (e1,…, еn) пространства V по следующему правилу
столбцами которой являются координаты образов базисных элементов, называется матрицей линейного оператора А в базисе e.
Пример:
Матрица D(с) оператора дифференцирования V: Мз → Mз в базисе ео = l. e1 = t, 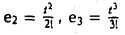
Пример:
Матрица D(e) оператора дифференцирования V: T2 → T2 в базисе e1 = cos t, е2 = sin t имеет вид
У = Ax.
Разложим элементы x и у no базису e:
элементов х и у в базисе с связаны соотношением
у(e) = A(e)х(e). (1)
в силу единственности разложения элемента у по базису e получаем
Записывая полученные п равенств в матричной форме
получаем требуемое равенство (1).
Теорема:
Ранг матрицы А(с) линейного оператора А: V —> V не зависит от выбора базиса с и равен рангу rang А оператора А.
то rang A равен максимальному числу линейно независимых элементов в системе Ае1,…, Аеn. В силу теоремы 4 главы V, последнее совпадает с максимальным числом линейно независимых столбцов матрицы А(e), т. е. с ее рангом. Таким образом,
rang А(с) = rang A.
Легко убедиться в том, что при сложении линейных операторов их матрицы (вычисленные в одном базисе) складываются, а при умножении линейного оператора на число его матрица умножается на это число.
Матрица произведения С = ВА операторов А и B равна произведению матриц этих операторов (относительно одного и того же базиса e):
С(e) = В(e)А(e). (2)
Вследствие того, что 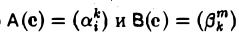
С (e) = В(e)А(e).
Отсюда, в частности, вытекает, что
матрица оператора A -1 , обратного к A, является обратной к его матрице А.
В самом деле, из соотношений
определяющих обратный оператор, получаем, что его матрица В удовлетворяет равенствам
ВА = I, АВ = I,
и, значит, является обратной к А:
В = A -1 .
Теорема:
Матрицы А = А(е) и А’ = А(е’) линейного оператора А: V → V относительно базисов с и с’ пространства V связаны равенством
где S — матрица перехода от базиса е к базису е’.
Пусть у = Ах. Координатные столбцы элементов х и у относительно базисов с и с’ связаны равенствами
у(е) = Ах (е), у(е’) = А’х(е’) (6)
соответственно. Согласно свойству 2 матрицы перехода имеем
х(е) = Sx(c’), у(е) = Sy(е’). (7)
Заменяя в первом из равенств (6) столбцы х(е) и у(е) их выражениями (7), получаем
Sy(е’) = ASx(е’).
Пользуясь вторым равенством (6), имеем
SA’x(е’) = ASx(е’).
Отсюда в силу произвольности столбца х(е’) получаем, что
SA’ = AS.
Так как матрица перехода S невырождена и, значит, обратима, то умножая обе части последнего равенства на матрицу S -1 слева приходим к требуемой формуле (5).
Следствие:
Определитель матрицы линейного оператора не зависит от выбора базиса.
Вычислим определитель матрицы
Последнее равенство выполняется в силу того, что
Таким же свойством обладает и определитель матрицы линейного оператора
А — tI,
где I — тождественный оператор, a t — произвольное число. * Рассмотрим матрицы этого оператора в базисах e и e’ соответственно:
Воспользовавшись равенством (5)
и доказанным выше следствием, получаем, что
Пусть 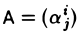
является многочленом от t и, согласно только что доказанному, не зависит от выбора базиса. Расписав определитель матрицы А — t1 подробнее, получаем, что
называется характеристическим многочленом линейного оператора А (матрицы А). Его корни называются характеристическими, или собственными, числами линейного оператора А (матрицы А).
Видео:Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать

Собственные значения и собственные элементы
Ненулевой элемент х ∈ V называется собственным элементом линейного оператора А: V —> V, если найдется такое число λ — собственное значение линейного оператора А, что
Ах = λх.
Пример:
Всякий многочлен нулевой степени является собственным элементом оператора дифференцирования
соответствующее собственное значение равно нулю:
Пример:
Оператор дифференцирования собственных элементов не имеет.
Пусть некоторый тригонометрический многочлен a cos t + β sin t после дифференцирования переходит в пропорциональный:
Это означает, что
Последнее равенство выполняется в том и только в том случае, если
откуда вытекает, что а = β = 0 и, значит, многочлен может быть только нулевым.
Теорема:
Вещественное число λ является собственным значением линейного оператора А в том и только в том случае, когда это число — корень его характеристического многочлена: х( λ ) = 0.
Необходимость, Пусть λ — собственное значение оператора А. Тогда найдется ненулевой элемент х, для которого Ах = λх.
Пусть е = (е1 …, еп) — базис пространства. Тогда последнее равенство можно переписать в эквивалентном матричном виде
Из того, что х — собственный элемент, вытекает, что его координатный столбец х(е) ненулевой. Это означает, что линейная система (1) имеет ненулевое решение. Последнее возможно лишь при условии, что
x (λ) = у.
Достаточность. Способ построения собственного элемента
Пусть λ — корень многочлена т- е-
Рассмотрим однородную линейную систему с матрицей А(е) — λ1:
В силу условия (2) эта система имеет ненулевое решение 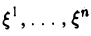
Построим элемент х по правилу
Координатный столбец х(е) этого элемента удовлетворяет условию
Последнее эквивалентно тому, что
Ах = λх.
Следовательно, х — собственный элемент линейного оператора λ, а А — соответствующее ему собственное значение.
Замечание:
Для нахождения всех собственных элементов, отвечающих заданному собственному значению λ, необходимо построить ФСР системы (3).
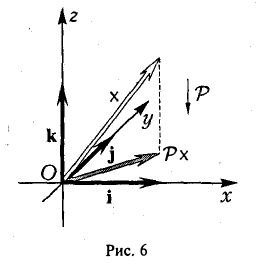
Пример:
Найти собственные векторы линейного оператора
действующего по правилу
(оператор проектирования) (рис.6).
Рассмотрим действия линейного оператора Р на базисные векторы. Имеем
Запишем матрицу оператора:
построим характеристический многочлен
и найдем его корни. Имеем λ1 = λ2,з = 1. Построим однородные линейные системы с матрицами:
Найдем фундаментальные системы решений для каждой из этих систем. Имеем
Таким образом, собственными векторами этого оператора проектирования являются: вектор к с собственным значением 0 и любой вектор 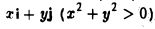
Пример:
Найти собственные элементы линейного оператора дифференцирования D, действующего в пространстве M3 многочленов степени не выше двух:
Матрица D заданного оператора в базисе I, t, t 2 имеет вид
характеристический многочлен — λ 3 имеет ровно один корень λ = 0. Решением системы
является набор 1,0,0, которому соответствует многочлен нулевой степени.
Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Сопряженный оператор
В евклидовом пространстве над линейными операторами можно ввести еще одно действие — операцию сопряжения.
Пусть V — n-мерное евклидово пространство. С каждым линейным оператором
A: V → V,
действующим в этом пространстве; естественно связан другой линейный оператор, сопряженный данному.
Определение:
Л*: V → V
(читается: «а со звездой») называется сопряженным линейному оператору А: V → , если для любых элементов х и у из пространства V выполняется равенство
(Ах, у) = (х, A*у). (1)
Линейный оператор А*, сопряженный данному оператору А, всегда существует.
Пусть e = (e1…..еn) — ортобазис пространства V и А = А(e) = 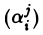
Непосредственными вычислениями можно убедиться в том, что для линейного оператора А*: V —> V, определяемого по правилу
равенство (1) выполнено при любых х и у. Напомним. что согласно теореме 1, для того, чтобы построить линейный оператор, достаточно задать его действие на базисные элементы.
Пример:
Введем в линейном пространстве М многочленов с вещественными коэффициентами степени не выше первой операцию скалярного умножения по следующему правилу. Пусть
Тем самым, М1 — двумерное евклидово пространство.
Пусть D: М1 — М1 — оператор дифференцирования-. D(a + bt) = b. Построим сопряженный оператор D*: М1 → М1.
Многочлены l и t образуют ортобазис пространства Af (, так как согласно правилу (*) (1. 1) = (t, t) = 1. (l, t) = 0. Матрица оператора D в этом базисе имеет вид
т.к. D(1) = 0, D(t) = 1. Тогда
— матрица сопряженного оператора D* действующего по правилу:
D*(l)=l, D*(t)=0.
Для произвольного многочлена φ(t) = а +bt получаем
Свойства операции сопряжения
- У каждого линейного оператора существует ровно один сопряженный ему оператор.
Пусть В и С — операторы, сопряженные заданному оператору A. Это означает, что для любых элементов х и у из пространства V выполняются равенства
(Ах, у) = (х, By), (Ах, у) = (х, Су).
Отсюда вытекает, что
(х, Ву)=(х, Су)
(х, By — Су) = 0.
В силу произвольности выбора элемента х заключаем, что элемент Ву-Су ортогонален любому элементу пространства V и, в частности, себе самому. Последнее возможно лишь в случае, когда By — Су = θ и, значит, By = Су. Вследствие того, что у — произвольный элемент, получаем В = С.
2. (аA)* = аA*, где а — произвольное вещественное число.
Пусть A: V —> V н B: V → V — линейные операторы. Тогда
Свойства 2-5 легко вытекают из единственности сопряженного оператора.
6. Пусть e — ортобазис пространства V. Для того, чтобы операторы А: V —> V и В: V —> V были взаимносопряженными, т.е. выполнялись равенства В = А, А= В, необходимо и достаточно, чтобы их матрицы А = А(e) и В = В(e) получались одна из другой транспонированием.
Замечание:
Подчеркнем, что свойство 6 справедливо только для матриц, построенных в ортонормиро-ванном базисе. Для произвольного базиса оно неверно.
7. Если линейный оператор А невырожден, то сопряженный ему оператор А* также невырожден и выполняется равенство
Видео:Образ линейного оператора. ПримерСкачать

Симметричный оператор
Линейный оператор А называется самосопряженным (или симметричным), если он совпадает с сопряженным ему оператором А*, т. е.
А* = А.
В силу свойства 6 из предыдущего параграфа матрица самосопряженного оператора в ортобазисе симметрична, т. е. не изменяется при транспонировании. Поэтому самосопряженный оператор называют также симметричным оператором.
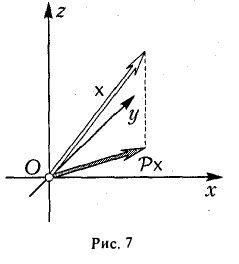
Пример:
Рассмотрим оператор Р ортогонального проектирования трехмерного евклидова пространства Oxyz на координатную плоскость Оху (рис. 7). В ортобазисе i,j,k матрица этого оператора имеет следующий вид
(так как Рi = i, Рj = j, Pk = θ, т. е. является симметричной. Значит, оператор проектирования P симметричен.
Симметричный оператор обладает рядом замечательных свойств.
Свойства симметричного оператора
Первые два вытекают из его определения.
- Для того, чтобы линейный оператор А: V → V был симметричным, необходимо и достаточно, чтобы для любых элементов х и у из пространства V выполнялось равенство
(Ах, У) = (х, Aу). (6) - Для того, чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в (каком-нибудь) ортонормированном базисе была симметрична.
- Характеристический многочлен симметричного оператора (и симметричной матрицы) имеет только вещественные корни.
Напомним, что вещественный корень λ характеристического многочлена линейного оператора А является его собственным значением, т.е. существует ненулевой элемент х (собственный вектор оператора А), который оператор А преобразует так: Ах = λх.
4. Собственные элементы симметричного оператора, отвечающие различным собственным значениям, ортогональны.
Пусть x1 и х2 — собственные элементы оператора А,
И 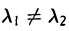
С другой стороны,
Из вытекающего отсюда равенства
Отсюда в силу неравенства 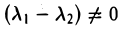
5. Пусть А: V —> V — симметричный оператор. Тогда в пространстве V существует ортонормированный базис е = (е1,… ,еп), состоящий из собственных элементов оператора А:
В приведенном выше примере таким базисом является тройка i, j, к: векторы i и j — собственные векторы оператора проектирования Р с собственными значениями, равными единице, а к — его собственный вектор с нулевым собственным значением.
6. Пусть А: V —» V — невырожденный симметричный оператор. Тогда обратный ему оператор А -1 : V —> V также является симметричным.
Замечание:
Все собственные значения невырожденного оператора отличны от нуля. Если λ ≠ 0 — собственное значение оператора А, то 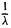
Симметричный оператор называется положительным, если для любого ненулевого элемента х из пространства V выполняется неравенство (Ах, х) > 0.
Свойства положительного оператора
- Симметричный оператор А: V —» V является положительным в том и только в том случае, когда все его собственные значения λ1…, λп положительны.
- Положительный оператор невырожден (обратим).
- Оператор, обратный положительному, также положителен.
Видео:Ядро и образ линейного оператораСкачать

Квадратичные формы
Пусть А = (aij) — симметричная матрица порядка п, ajj = Выражение
(1)
называется квадратичной формой переменных 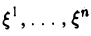
Примером квадратичной формы двух переменных х и у может служить выражение ах2 + 2bху + су2, где а, b и с — некоторые действительные числа; ее матрица
Набор чисел 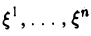
Тогда выражение (1) будет представлять собой числовую функцию аргумента х, заданную на всем пространстве V. Эту функцию принято обозначать так: A(х, х). О такой квадратичной форме
(2)
говорят, что она задана в n-мерном евклидовом пространстве
Со всякой квадратичной формой A(x, x) естественно связана симметричная билинейная форма
(3)
где 
Замечание:
Форма (3) называется билинейной, так как она линейна по каждому аргументу — и по х, и по у :
(здесь a1, a2, β1, β2 — произвольные числа).
Билинейная форма (3) называется симметричной вследствие того, что ее значение не зависит от порядка аргументов,
Вычисляя значения билинейной формы A (x, у) на базисных элементах, т. е. полагая х = еk, у = ет, получаем, что (4)
Это означает, что элементы матрицы А квадратичной формы (2) суть значения билинейной формы на элементах базиса с.
Примером билинейной формы может служить скалярное произведение векторов n-мерного координатного пространства Rn
где 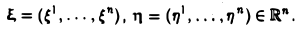
определяет квадрат длины вектора ξ.
При переходе к другому базису координаты элемента х изменяются. Меняется и матрица А = А(e) квадратичной формы.
В приложениях часто возникает необходимость приведения квадратичной формы к наиболее простому виду. Таким видом является диагональный, или нормальный вид. Будем говорить, что квадратичная форма в базисе с имеет нормальный вид, если все коэффициенты при произведениях различных координат равны нулю, т.е. аij = 0 при i ≠ j. Тогда
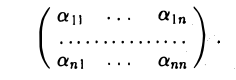
Матрица квадратичной формы в этом базисе имеет диагональный вид:
Теорема:
Для каждой квадратичной формы, заданной в евклидовом пространстве, можно указать (ортонормированный) базис, в котором ее матрица имеет диагональный вид.
Чтобы убедиться в справедливости этого утверждения, воспользуемся свойствами симметричного оператора. Построим линейный оператор А: V → V так, чтобы его матрица 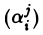
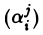
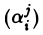
Вычислим (Aх, х). Замечая, что
вследствие ортонормированности базиса e, получаем
Тем самым, м ы установили важную связь
A(х, х) = (Aх, х) (5)
между квадратичной формой, заданной в евклидовом пространстве V, и действующим в нем симметричным оператором.
В силу симметричности построенного оператора А в евклидовом пространстве V существует ортонормированный базис f = (f1,… ,fn) состоящий из собственных элементов оператора А:
Разложим элемент х по базису f,
и вновь вычислим (Aх, х). Имеем
Отсюда в силу равенства (5) получаем, что
Тем самым, матрица A(f) исходной квадратичной формы в базисе f является диагональной:
Сам диагональный вид квадратичной формы можно (с точностью до порядка слагаемых) записать и не вычисляя элементов базиса f. Достаточно найти собственные значения линейного оператора А или, что тоже самое, собственные значения матрицы А = (aij) и выписать их с учетом кратности.
Пример:
Привести квадратичную форму
A(х, х) = 2ху + 2yz + 2xz
к диагональному виду.
Запишем матрицу квадратичной формы
и построим ее характеристический многочлен:
Приравняв полученное выражение к нулю, найдем его корни:
Построение соответствующего ортобазиxа сложнее.
Собственные векторы симметричного оператора А суть собственные векторы матрицы квадратичной формы. Найдем их.
Пусть λ = 2. Рассмотрим однородную линейную систему с матрицей
Все решения системы
пропорциональны набору (1 1 1 ) т.
Пусть λ = — I. Однородная линейная система с матрицей
сводится к одному уравнению
х + y + z = 0
и имеет два линейно независимых решения. Выберем их так, чтобы они были ортогональны: (1 -2 1 )Т, (1 0 — 1 )Т. Легко убедиться в том, что векторы с найденными координатными столбцами попарно ортогональны. Пронормируем их:
Искомый базис построен:
Замечание:
В качестве пространства V можно взять любое п-мерное евклидово пространство. Однако в задачах наиболее часто встречается координатное пространство Rn, элементами которого являются всевозможные упорядоченные наборы действительных чисел — ξ = (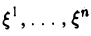
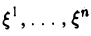

Опишем алгоритм, посредством которого для произвольной квадратичной формы, заданной в n-мерном координатном пространстве, строится базис, в котором эта квадратичная форма имеет диагональный вид.
— заданная квадратичная форма.
- Выпишем матрицу квадратичной формы
2. Построим характеристический многочлен
и найдем его корни (в силу симметричности матрицы все корни вещественны). Запишем их с учетом кратности:
3. Пусть λ — один из этих корней, кратности k. Однородная линейная система с матрицей
имеет ровно к линейно независимых решений (образующих фундаментальную систему решений). Ортонормировав ее, получим к попарно ортогональных решений единичной длины.
4. Поступая так с каждым корнем характеристического многочлена, получаем набор ровной попарно ортогональных элементов единичной длины, т. с. ортобазис f1 …, fn пространства Rn.
В построенном ортобазисе f = (f1,…,fn) заданная квадратичная форма имеет диагональный вид:
Определение:
называется положительно определенной или знакоположительной, если для любого ненулевого элемента х (или, что то же, для любого ненулевого набора 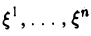
A(х, х) > 0.
Примером знакоположительной квадратичной формы может служить скалярный квадрат произвольного вектора ξ = (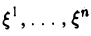
После приведения знакоположительной квадратичной формы к диагональному виду получаем
где λ1 > 0, …, λn > 0
Критерий Сильвестра (знакоположительное квадратичной формы)
Для того, чтобы квадратичная форма (6) была знакоположительной, необходимо и достаточно, чтобы все миноры ее матрицы, расположенные в левом верхнем углу, были положительны, т. е.
Метод Лагранжа
Существует еще один (простой) метод приведения квадратичной формы к диагональному виду, удобный, например, при получении ответа на вопрос, является ли квадратичная форма знакоопределенной или нет. Этот метод Лагранжа, или метод выделения полного квадрата, заключается в следующем. Пусть
— заданная квадратичная форма и a11 ≠ 0. Выпишем сначала все слагаемые, содержащие переменную ξ 1 и преобразуем их так:
Замечая, что выражение
также является квадратичной формой, но уже зависящей от меньшего числа переменных, вновь выделяем полный квадрат и т.д.
Если a11 = 0, но отлично от нуля аii(2
В результате проведенного преобразования координат, в частности, получим
И, тем самым, придем к общему случаю.
Пример:
Методом Лагранжа привести к диагональному виду квадратичную форму
A(x, х) = 2ху + 2yz + 2zx.
Введем новые координаты
Замечание:
Недостаток метола Лагранжа состоит в том, что при указанных преобразованиях координат новые координатные оси уже не являются попарно ортогональными.
Существуют и другие способы приведения квадратичной формы к диагональному виду.
Сравнивая результаты описанных выше двух способов приведения квадратичной формы 2ху + 2yz + 2zx к диагональному виду (речь идет о последних двух разобранных примерах), можно заметить, что в них соответственно одинаковы: число отрицательных коэффициентов и число положительных коэффициентов. Это совпадение не случайно, а является важным свойством квадратичных форм, называемым законом инерции:
число положительных, число отрицательных и число нулевых коэффициентов при квадратах неизвестных в диагональном виде квадратичной формы всегда одни и те же и не зависят от способа приведения квадратичной формы к этому виду.
Видео:Ядро и образ линейного оператора. ТемаСкачать

Классификация кривых и поверхностей второго порядка
Применим описанный выше алгоритм приведения квадратичной формы к диагональному виду для классификации кривых и поверхностей второго порядка.
Кривые
Рассмотрим общее уравнение кривой второго порядка на плоскости Оху :
Построим матрицу квадратичной части ах2 + 2bху+су2:
Найдем корни λ1 и λ2 характеристического многочлена и соответствующие им собственные векторы i и j (единичные и взаимноортогональные).. Возьмем эти векторы за орты новых осей Ох и Оу (рис. 8).
Переходя к новым координатам 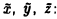
Возможны два случая: 1) λ1 • λ2 ≠ 0, 2) λ1 (или λ2 ) равно нулю.
В первом случае сдвигом точки начала отсчета
добиваемся исчезновения линейных членов
Далее, как это и делалось, рассматриваем всевозможные сочетания знаков у коэффициентов λ1, λ2 и f. В результате получаем: эллипс, гиперболу, пару пересекающихся прямых, точку, пустое множество.
Во втором случае (положим для определенности λ1 = 0, λ2 ≠ 0) сдвигом начала отсчета
приходим к уравнению
Если же d= 0,то взяв а = 0, имеем
В зависимости от знака 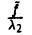
Замечание:
Операция отыскания корней характеристического многочлена квадратичной части уравнения кривой и взаимноортогональных единичных собственных векторов, описанная здесь, заменяет уничтожение произведения разноименных координат путем поворота на подходящий угол. В случае поверхностей второго порядка дело обстоит сложнее (и для того, чтобы разобраться с классификацией до конца, нужны и внимание и терпение).
Поверхности
Общее уравнение поверхности второго порядка имеет следующий вид
Упростим вид квадратичной части этого уравнения (подчеркнута), пользуясь описанным выше алгоритмом. Построим матрицу
найдем корни λ1, λ2, λз характеристического многочлена
и соответствующие им собственные векторы i, J, k так, чтобы они образовывали ортонормированную тройку (это всегда возможно). Возьмем векторы i, J и k за орты новых координатных осей Ox, Ox, Oz. Производя замену координат, получим (*)
Возможны три случая:
(I) Все три корня λ1, λ2, λ3 отличны от нуля. Путем сдвига начала
уравнение (*) поверхности приводится к следующему виду
имеют один и тот же знак, противоположный знаку 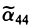
получаем уравнение эллипсоида
β ) Знаки λ1 и λ2 противоположны знаку 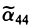
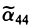
получаем уравнение однополостного гиперболоида
γ ) Знаки λ1 и λ2 совпадают со знаком 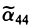
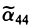
получаем уравнение двуполостного гиперболоида
б. 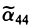
а) Если λ1, λ2 и λз имеют один и тот же знак, то получаем точку (0, 0, 0).
β) Если одно из λ, имеет знак, противоположный знаку двух других, то получаем уравнение конуса второго порядка
(II) Ровно один корень равен нулю (для определенности λз = 0). Полагая
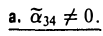
получаем уравнение вида
а) Если λ1 и λ2 — одного знака, то, полагая
(можно считать, что знак 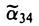
β) Если λ1 и λ2 имеют противоположные знаки, то, положив
получим уравнение гиперболического параболоида
б. 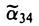
Классификация поверхностей с уравнениями такого типа приводится в таблице.
Замечание:
Отсутствие третьей координаты (точнее, ее неявное присутствие) приводит к цилиндрическим поверхностям, направляющими которых являются кривые второго порядка, лежащие в плоскости Z = 0 и имеющие уравнения вила
(III) Ровно два корня равны нулю (для определенности λ2 = λ3 = 0). Преобразованием координат
приходим к уравнению
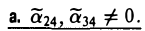
уравнение поверхности приводится к следующему виду
Замечание:
Преобразование координат, упрощающее вид уравнения, выбирается так, чтобы новая координатная система вновь была прямоугольной декартовой.
Сдвигом начала координат
получаем уравнение параболического цилиндра
описывает либо пару параллельных плоскостей ( λ1 • 
Видео:Образ, ядро, собственные векторы линейного оператораСкачать
Дополнение к линейным отображениям





Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:



















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:11.1 Образ и ядро линейного оператораСкачать

Линейные операторы
Видео:Матрица линейного оператораСкачать

1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы 

| y=Ax, | (1) |
где A — m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
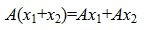 , , | (2) |
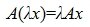 . . |
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов 

Пусть x − произвольный элемент в R. Тогда
 | (3) |
является разложением x в по базису 
Применим оператор A к базисным векторам 
 | (4) |
где aij − координаты полученного вектора в базисе 
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
Сделаем следующее обозначение:
 | (6) |
Тогда равенство (5) примет следующий вид:
 | (7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе 
Построим матрицу A с элементами aij:
 | (8) |
Тогда выражение (6) можно записать в матричном виде:
| y=Ax. | (9) |
Матрица A называется матрицей линейного оператора в заданных базисах 

Видео:Линейные операторы.Скачать
2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B — mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
| Cx= Ax+ Bx, x∈R, | (10) |
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej= Aej+ Bej= | n | (aij+bij) ej |
| ∑ | ||
| j= 1 |
Следовательно оператору C отвечает матрица 
| C=A+B. | (11) |
Видео:Образуют ли данные векторы базисСкачать

3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
| Cx= A( Bx), x ∈ R. | (12) |
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
| y=Bx, z=Ay, z=Cx |
можно записать в виде матричных равенств
| y=Bx, z=Ay, z=Cx |
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
| Cx=A(Bx)=(AB)x. |
Учитывая произвольность х, получим
| C=AB. | (13) |
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
Видео:Матрица линейного оператора (01)Скачать

4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
| Cx=λ ( Ax) | (14) |
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
| y=Ax, z=λy, z=Cx |
можно записать в виде матричных равенств
| y=Ax, z=λy, z=Cx |
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
| Cx=λ(Ax)=(λA)x. |
Учитывая произвольность х, получим
| C=λA. | (15) |
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
Видео:7 2 Матрица линейного оператораСкачать

5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
Видео:7 4 Собственные векторы и собственные значенияСкачать

6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
Видео:Вышмат. Введение в линейные операторыСкачать

7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
Видео:Координаты в новом базисеСкачать

8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
Матрица линейного оператора примеры
Построение матрицы по заданной формуле отображения.
Пусть отображение задано с помощью формулы:
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор 
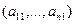
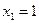
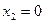
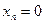
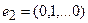
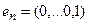
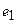
Пример 1. Пусть оператор задан с помощью формулы:
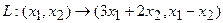
Прежде всего, докажем, что это отображение – действительно линейный оператор.
Отобразим сумму векторов:
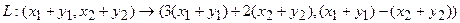
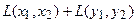
Аналогично для умножения на константу:
Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x1 = 1, x2 = 0, а затем x1 = 0, x2 = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).
Поэтому матрица линейного оператора будет иметь вид:
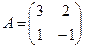
Аналогичным способом решается задача и для 3 и большего количества переменных.
Пример 2. 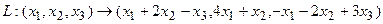
Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).
Матрица линейного оператора:
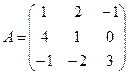
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.
Если задана система 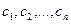
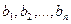
Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.
Пусть 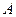
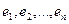
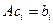
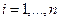
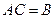
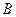
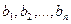
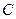
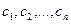
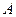
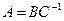
Пример. Найти матрицу линейного оператора, отображающего базис
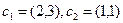
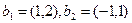
Здесь 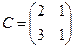
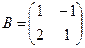
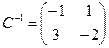
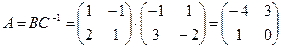
Проверка осуществляется умножением получившейся матрицы на каждый вектор: 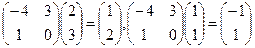
Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.
2.3. Прочие способы нахождения матрицы оператора.
Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида 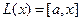
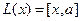
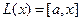
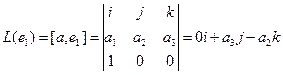
Аналогично, 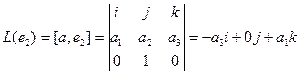
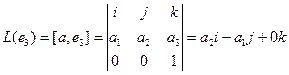
Координаты полученных векторов запишем в виде столбцов матрицы оператора.
Матрица оператора: 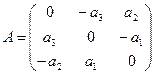
Аналогично можно построить матрицу линейного оператора 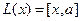
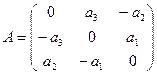
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы 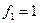
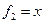
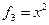
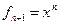
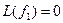
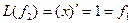
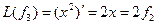
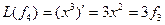
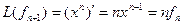
Матрица этого линейного оператора:
Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Матрица линейного оператора
Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:
Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:
Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .
Разложим векторы x и y по базису e 1 ,e 2 . e n :
В силу линейности оператора A можно написать
Заметим, что каждый вектор 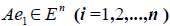
В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:
Получили, что линейному оператору A в данном базисе соответствует квадратная матрица
которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .
Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .
Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .
Примеры линейных операторов
1. В пространстве 2-мерных векторов линейным оператором является правило
связывающее вектор-прообраз 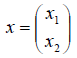
2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.
3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .
Пример: Известны образы базисных векторов E 3 под действием оператора A :
Найти матрицу этого оператора в исходном базисе.
Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем
Действия над операторами
Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.
Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .
Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .
Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.
Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством 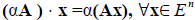
?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.
Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .
Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .
Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .
Рассмотрим матрицы – столбцы:
и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.
a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y
б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x
Свойства умножения линейных операторов вытекают из свойств умножения матриц.
Определение 4. Линейные операторы A и В называются равными, если 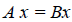
Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 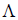
1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы 

| y=Ax, | (1) |
где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
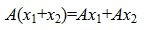 , , | (2) |
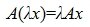 . . |
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов 

Пусть x − произвольный элемент в R. Тогда
 | (3) |
является разложением x в по базису 
Применим оператор A к базисным векторам 
 | (4) |
где aij − координаты полученного вектора в базисе 
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
Сделаем следующее обозначение:
 | (6) |
Тогда равенство (5) примет следующий вид:
 | (7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе 
Построим матрицу A с элементами aij:
 | (8) |
Тогда выражение (6) можно записать в матричном виде:
| y=Ax. | (9) |
Матрица A называется матрицей линейного оператора в заданных базисах 

2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
| Cx= Ax+ Bx, x∈R, | (10) |
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej= Aej+ Bej= | n | (aij+bij) ej |
| ∑ | ||
| j= 1 |
Следовательно оператору C отвечает матрица 
| C=A+B. | (11) |
3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
| Cx= A( Bx), x ∈ R. | (12) |
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
| y=Bx, z=Ay, z=Cx |
можно записать в виде матричных равенств
| y=Bx, z=Ay, z=Cx |
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
| Cx=A(Bx)=(AB)x. |
Учитывая произвольность х, получим
| C=AB. | (13) |
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
| Cx=λ ( Ax) | (14) |
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
| y=Ax, z=λy, z=Cx |
можно записать в виде матричных равенств
| y=Ax, z=λy, z=Cx |
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
| Cx=λ(Ax)=(λA)x. |
Учитывая произвольность х, получим
| C=λA. | (15) |
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
Линейное отображение с примерами решения и образцами выполнения
Линейное отображение — обобщение линейной числовой функции, а точнее, функции на случай более общего множества аргументов и значений. Линейные отображения, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.
Определение линейного отображения. Образ и ядро линейного отображения
Пусть V и W — линейные пространства (либо оба вещественные, либо оба комплексные). Линейным отображением линейного пространства V в линейное пространство W называется правило А, согласно которому каждому элементу х из пространства V ставится в соответствие (единственный) элемент у = Ах из пространства W так, что
Эти два требования можно объединить в одно:
Обозначение: A:V → W.
Примеры линейных отображений
- Пусть V = W = Мп, где Мп — пространство многочленов, степень которых не выше п. Правило
согласно которому каждому многочлену из Мп ставится в соответствие его производная, является линейным отображением (производная суммы равна сумме производных, постоянный сомножитель можно выносить из-под знака производной).
2. Правило, по которому каждому элементу х из V ставится в соответствие элемент λх из V ( λ ≠ 0 и фиксировано), — преобразование подобия — является линейным отображением (рис. 1).
3. Пусть у = (еi…, еn) — базис пространства V. Поставим произвольному элементу
в соответствие элемент
(здесь k
4. Cовокупность Т2 тригонометрических многочленов вида
образует линейное пространство. Правило
является линейным отображением
5. Пусть 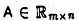
Образом линейного отображения А: V → W называется множество im А всех элементов из пространства W, обладающих следующим свойством элемент у лежит в im А, если в пространстве V найдется элемент х, такой, что Ах = у. Примеры.
1′. Образом операции дифференцирования V : Мn — Мп является совокупность многочленов, степень которых не выше п — 1,
2′. Образ отображения подобия совпадает со всем пространством V.
3′. Образ отображения проектирования V : V → V является подпространством
4′. Образ операции дифференцирования V : T2 → Т2 совпадает со всем пространством Т2
Теорема:
Образ im А линейного отображения А: V → W является линейным подпространством пространства W.
Пусть у1 и у2 — элементы из im А. Это означает, что в пространстве V найдутся элементы x1 и х2, такие, что -Ax1 = y1 и Ах2 = у2. Из формулы
вытекает, что произвольная линейная комбинация элементов y1 и у2 также лежит в im А.
Размерность образа линейного отображения называется рангом этого линейного отображения.
Обозначение: rang А.
Определение:
Линейные отображения А: V → W и В: V W называются равными, если для любого элемента х из пространства V выполняется равенство Ах = Вх.
Обозначение: А = В.
Теорема:
Построение линейного отображения. Пусть V и W — линейные пространства, e = (e1… , еn) — базис пространства V, a f1. . ., fn — произвольные элементы из пространства W. Тогда существует и притом ровно одно линейное отображение
A :V → W,
А. Существование. Разложим произвольный элемент х из пространства V по базису с этого пространства,
и построим отображение А: V → W по следующему правилу:
В линейности отображения А убедимся непосредственно. Пусть
Тогда согласно правилу (2)
Б. Единственность. Покажем, что требованием (1) линейное отображение А определяется однозначно.
Пусть В: V → W — линейное отображение и
Вычисляя действия А и В на произвольный элемент х из V, убеждаемся в том, что в обоих случаях результат один и тот же —
Значит, отображения A и В совпадают.
Таким образом, линейное отображение можно задать его действием только на элементы базиса.
Ядром линейного отображения А: V → W называется множество ker А всех элементов из пространства V, каждый из которых отображение А переводит в нулевой элемент θw пространства W.
Примеры:
1″. Многочлены нулевой степени образуют ядро операции дифференцирования V: Мп -> Мп.
2″. Ядро отображения подобия состоит из нулевого элемента θv пространства V.
3″. Ядром отображения проектирования P: V→V является линейное подпространство L(ek+1,…, еn) (рис. 3).
4″. Ядро операции дифференцирования D:T2→Т2 состоит из нуля.
5″. Ядром отображения
является множество решений однородной линейной системы
АХ = 0.
Теорема:
Ядро линейного отображения А: V
→W является линейным подпространством пространства V.
Из равенств Ах = θw и Ay = θw вытекает, что
Размерность ядра линейного отображения называется дефектом этого отображения.
Обозначение: defect . Операции над линейными отображениям
Пусть V и W — линейные пространства и A:V W, B:V→W — линейные отображения. Суммой линейных отображений А и В называется отображение С: V→W, определяемое п о следующему правилу:
Сх = Ах + Вх
для любого элемента х из V. Нетрудно убедиться в том, что отображение С является линейным. В самом деле,
Обозначение: С = А + В.
Произведением линейного отображения A:V→W на число а называется отображение В: V —> W, определяемое по правилу:
Вх = аАх
для любого элемента х из V. Отображение В линейно:
Обозначение: В = а А.
В дальнейшем мы ограничимся рассмотрением линейных операторов — линейных отображений, действующих из пространства V в это же пространство V. Среди рассмотренных выше примеров отображений линейными операторами являются дифференцирование, подобие и проектирование; умножение столбца на квадратную матрицу также является линейным оператором.
Оператор I: V —> V, задаваемый правилом Ix = х для любого элемента х из V, называется тождественным.
Введем операцию умножения линейных операторов. Пусть А: V → V и В: V→V — линейные операторы. Произведением оператора А на оператор В называется отображение С: V → V, определяемое по правилу
Сх = В(Ах),
где х — произвольный элемент из V. Покажем, что С — линейный оператор:
Обозначение: С = В А.
Замечание:
Порядок сомножителей в произведении линейных операторов является существенным, как показывает следующий пример.
Пример:
Пусть V = R 2 . Отображения
— линейные операторы, действующие из R 2 в R 2 (рис. 4). Тогда
Пусть A: V → V — линейный оператор. Линейный оператор В: V → V называется обратным оператору А, если выполнены следующие равенства
ВА = АВ= I,
где I: V —> V — тождественный оператор.
Теорема:
Для того, чтобы у линейного оператора А: V → V был обратный, необходимо и достаточно, чтобы образ оператора А совпадал со всем пространством,
im А = V.
Предположим сначала, что обратный оператор В у заданного оператора А существует и покажем, что произвольно взятый элемент у из пространства V непременно лежит в im А. Подействовав оператором А на элемент х = В у, согласно определению (1), получим
Ах = А(Ву) = (АВ)у = Iу — у.
Значит, элемент у является образом элемента х = By и, следовательно, лежит в im А. Тем самым imA = V.
Пусть теперь образ оператора А совпадает со всем пространством V:
imA = V.
rang А = dim V.
Поэтому оператор А переводит базис пространства V снова в базис:
Построим линейный оператор В по следующему правилу
Согласно теореме 1, условием (2) оператор В определяется однозначно.
Пусть х — произвольный элемент пространства V. Вычислим (ВA)х и (АВ)х. Разложим х по базису с. Имеем
Подействовав на него оператором В А, с учетом формул (2) получаем, что
Аналогично, раскладывая элемент х по базису f,
и действуя на него оператором АВ, имеем
ВAх = х, АВх = х
для любого элемента х из V и, значит,
В А = АВ = I.
Замечание:
В ходе доказательства этой теоремы мы установили также, что обратный к А оператор В определен однозначно.
Для оператора, обратного к А, принято следующее обозначение: А -1 .
Следствие:
Линейный оператор А: V → V обратим (имеет обратный) тогда и только тогда, когда его ядро тривиально,
ker А= < θ v>.
Справедливость этого утверждения вытекает из теоремы 3 и формулы.
Пример:
осуществляет равномерное сжатие плоскости к оси ξ 1 (с коэффициентом
— равномерное растяжение (с коэффициентом 3/2) (рис. 5).
Матрица линейного оператора
Пусть линейный оператор А: V —> V преобразует элементы базиса e = (e1,…, еn) пространства V по следующему правилу
столбцами которой являются координаты образов базисных элементов, называется матрицей линейного оператора А в базисе e.
Пример:
Матрица D(с) оператора дифференцирования V: Мз → Mз в базисе ео = l. e1 = t, 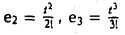
Пример:
Матрица D(e) оператора дифференцирования V: T2 → T2 в базисе e1 = cos t, е2 = sin t имеет вид
У = Ax.
Разложим элементы x и у no базису e:
элементов х и у в базисе с связаны соотношением
у(e) = A(e)х(e). (1)
в силу единственности разложения элемента у по базису e получаем
Записывая полученные п равенств в матричной форме
получаем требуемое равенство (1).
Теорема:
Ранг матрицы А(с) линейного оператора А: V —> V не зависит от выбора базиса с и равен рангу rang А оператора А.
то rang A равен максимальному числу линейно независимых элементов в системе Ае1,…, Аеn. В силу теоремы 4 главы V, последнее совпадает с максимальным числом линейно независимых столбцов матрицы А(e), т. е. с ее рангом. Таким образом,
rang А(с) = rang A.
Легко убедиться в том, что при сложении линейных операторов их матрицы (вычисленные в одном базисе) складываются, а при умножении линейного оператора на число его матрица умножается на это число.
Матрица произведения С = ВА операторов А и B равна произведению матриц этих операторов (относительно одного и того же базиса e):
С(e) = В(e)А(e). (2)
Вследствие того, что 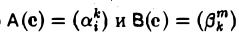
С (e) = В(e)А(e).
Отсюда, в частности, вытекает, что
матрица оператора A -1 , обратного к A, является обратной к его матрице А.
В самом деле, из соотношений
определяющих обратный оператор, получаем, что его матрица В удовлетворяет равенствам
ВА = I, АВ = I,
и, значит, является обратной к А:
В = A -1 .
Теорема:
Матрицы А = А(е) и А’ = А(е’) линейного оператора А: V → V относительно базисов с и с’ пространства V связаны равенством
где S — матрица перехода от базиса е к базису е’.
Пусть у = Ах. Координатные столбцы элементов х и у относительно базисов с и с’ связаны равенствами
у(е) = Ах (е), у(е’) = А’х(е’) (6)
соответственно. Согласно свойству 2 матрицы перехода имеем
х(е) = Sx(c’), у(е) = Sy(е’). (7)
Заменяя в первом из равенств (6) столбцы х(е) и у(е) их выражениями (7), получаем
Sy(е’) = ASx(е’).
Пользуясь вторым равенством (6), имеем
SA’x(е’) = ASx(е’).
Отсюда в силу произвольности столбца х(е’) получаем, что
SA’ = AS.
Так как матрица перехода S невырождена и, значит, обратима, то умножая обе части последнего равенства на матрицу S -1 слева приходим к требуемой формуле (5).
Следствие:
Определитель матрицы линейного оператора не зависит от выбора базиса.
Вычислим определитель матрицы
Последнее равенство выполняется в силу того, что
Таким же свойством обладает и определитель матрицы линейного оператора
А — tI,
где I — тождественный оператор, a t — произвольное число. * Рассмотрим матрицы этого оператора в базисах e и e’ соответственно:
Воспользовавшись равенством (5)
и доказанным выше следствием, получаем, что
Пусть 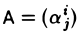
является многочленом от t и, согласно только что доказанному, не зависит от выбора базиса. Расписав определитель матрицы А — t1 подробнее, получаем, что
называется характеристическим многочленом линейного оператора А (матрицы А). Его корни называются характеристическими, или собственными, числами линейного оператора А (матрицы А).
Собственные значения и собственные элементы
Ненулевой элемент х ∈ V называется собственным элементом линейного оператора А: V —> V, если найдется такое число λ — собственное значение линейного оператора А, что
Ах = λх.
Пример:
Всякий многочлен нулевой степени является собственным элементом оператора дифференцирования
соответствующее собственное значение равно нулю:
Пример:
Оператор дифференцирования собственных элементов не имеет.
Пусть некоторый тригонометрический многочлен a cos t + β sin t после дифференцирования переходит в пропорциональный:
Это означает, что
Последнее равенство выполняется в том и только в том случае, если
откуда вытекает, что а = β = 0 и, значит, многочлен может быть только нулевым.
Теорема:
Вещественное число λ является собственным значением линейного оператора А в том и только в том случае, когда это число — корень его характеристического многочлена: х( λ ) = 0.
Необходимость, Пусть λ — собственное значение оператора А. Тогда найдется ненулевой элемент х, для которого Ах = λх.
Пусть е = (е1 …, еп) — базис пространства. Тогда последнее равенство можно переписать в эквивалентном матричном виде
Из того, что х — собственный элемент, вытекает, что его координатный столбец х(е) ненулевой. Это означает, что линейная система (1) имеет ненулевое решение. Последнее возможно лишь при условии, что
x (λ) = у.
Достаточность. Способ построения собственного элемента
Пусть λ — корень многочлена т- е-
Рассмотрим однородную линейную систему с матрицей А(е) — λ1:
В силу условия (2) эта система имеет ненулевое решение 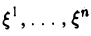
Построим элемент х по правилу
Координатный столбец х(е) этого элемента удовлетворяет условию
Последнее эквивалентно тому, что
Ах = λх.
Следовательно, х — собственный элемент линейного оператора λ, а А — соответствующее ему собственное значение.
Замечание:
Для нахождения всех собственных элементов, отвечающих заданному собственному значению λ, необходимо построить ФСР системы (3).
Пример:
Найти собственные векторы линейного оператора
действующего по правилу
(оператор проектирования) (рис.6).
Рассмотрим действия линейного оператора Р на базисные векторы. Имеем
Запишем матрицу оператора:
построим характеристический многочлен
и найдем его корни. Имеем λ1 = λ2,з = 1. Построим однородные линейные системы с матрицами:
Найдем фундаментальные системы решений для каждой из этих систем. Имеем
Таким образом, собственными векторами этого оператора проектирования являются: вектор к с собственным значением 0 и любой вектор 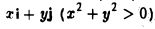
Пример:
Найти собственные элементы линейного оператора дифференцирования D, действующего в пространстве M3 многочленов степени не выше двух:
Матрица D заданного оператора в базисе I, t, t 2 имеет вид
характеристический многочлен — λ 3 имеет ровно один корень λ = 0. Решением системы
является набор 1,0,0, которому соответствует многочлен нулевой степени.
Сопряженный оператор
В евклидовом пространстве над линейными операторами можно ввести еще одно действие — операцию сопряжения.
Пусть V — n-мерное евклидово пространство. С каждым линейным оператором
A: V → V,
действующим в этом пространстве; естественно связан другой линейный оператор, сопряженный данному.
Определение:
Л*: V → V
(читается: «а со звездой») называется сопряженным линейному оператору А: V → , если для любых элементов х и у из пространства V выполняется равенство
(Ах, у) = (х, A*у). (1)
Линейный оператор А*, сопряженный данному оператору А, всегда существует.
Пусть e = (e1…..еn) — ортобазис пространства V и А = А(e) = 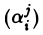
Непосредственными вычислениями можно убедиться в том, что для линейного оператора А*: V —> V, определяемого по правилу
равенство (1) выполнено при любых х и у. Напомним. что согласно теореме 1, для того, чтобы построить линейный оператор, достаточно задать его действие на базисные элементы.
Пример:
Введем в линейном пространстве М многочленов с вещественными коэффициентами степени не выше первой операцию скалярного умножения по следующему правилу. Пусть
Тем самым, М1 — двумерное евклидово пространство.
Пусть D: М1 — М1 — оператор дифференцирования-. D(a + bt) = b. Построим сопряженный оператор D*: М1 → М1.
Многочлены l и t образуют ортобазис пространства Af (, так как согласно правилу (*) (1. 1) = (t, t) = 1. (l, t) = 0. Матрица оператора D в этом базисе имеет вид
т.к. D(1) = 0, D(t) = 1. Тогда
— матрица сопряженного оператора D* действующего по правилу:
D*(l)=l, D*(t)=0.
Для произвольного многочлена φ(t) = а +bt получаем
Свойства операции сопряжения
- У каждого линейного оператора существует ровно один сопряженный ему оператор.
Пусть В и С — операторы, сопряженные заданному оператору A. Это означает, что для любых элементов х и у из пространства V выполняются равенства
(Ах, у) = (х, By), (Ах, у) = (х, Су).
Отсюда вытекает, что
(х, Ву)=(х, Су)
(х, By — Су) = 0.
В силу произвольности выбора элемента х заключаем, что элемент Ву-Су ортогонален любому элементу пространства V и, в частности, себе самому. Последнее возможно лишь в случае, когда By — Су = θ и, значит, By = Су. Вследствие того, что у — произвольный элемент, получаем В = С.
2. (аA)* = аA*, где а — произвольное вещественное число.
Пусть A: V —> V н B: V → V — линейные операторы. Тогда
Свойства 2-5 легко вытекают из единственности сопряженного оператора.
6. Пусть e — ортобазис пространства V. Для того, чтобы операторы А: V —> V и В: V —> V были взаимносопряженными, т.е. выполнялись равенства В = А, А= В, необходимо и достаточно, чтобы их матрицы А = А(e) и В = В(e) получались одна из другой транспонированием.
Замечание:
Подчеркнем, что свойство 6 справедливо только для матриц, построенных в ортонормиро-ванном базисе. Для произвольного базиса оно неверно.
7. Если линейный оператор А невырожден, то сопряженный ему оператор А* также невырожден и выполняется равенство
Симметричный оператор
Линейный оператор А называется самосопряженным (или симметричным), если он совпадает с сопряженным ему оператором А*, т. е.
А* = А.
В силу свойства 6 из предыдущего параграфа матрица самосопряженного оператора в ортобазисе симметрична, т. е. не изменяется при транспонировании. Поэтому самосопряженный оператор называют также симметричным оператором.
Пример:
Рассмотрим оператор Р ортогонального проектирования трехмерного евклидова пространства Oxyz на координатную плоскость Оху (рис. 7). В ортобазисе i,j,k матрица этого оператора имеет следующий вид
(так как Рi = i, Рj = j, Pk = θ, т. е. является симметричной. Значит, оператор проектирования P симметричен.
Симметричный оператор обладает рядом замечательных свойств.
Свойства симметричного оператора
Первые два вытекают из его определения.
- Для того, чтобы линейный оператор А: V → V был симметричным, необходимо и достаточно, чтобы для любых элементов х и у из пространства V выполнялось равенство
(Ах, У) = (х, Aу). (6) - Для того, чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в (каком-нибудь) ортонормированном базисе была симметрична.
- Характеристический многочлен симметричного оператора (и симметричной матрицы) имеет только вещественные корни.
Напомним, что вещественный корень λ характеристического многочлена линейного оператора А является его собственным значением, т.е. существует ненулевой элемент х (собственный вектор оператора А), который оператор А преобразует так: Ах = λх.
4. Собственные элементы симметричного оператора, отвечающие различным собственным значениям, ортогональны.
Пусть x1 и х2 — собственные элементы оператора А,
И 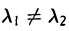
С другой стороны,
Из вытекающего отсюда равенства
Отсюда в силу неравенства 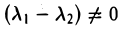
5. Пусть А: V —> V — симметричный оператор. Тогда в пространстве V существует ортонормированный базис е = (е1,… ,еп), состоящий из собственных элементов оператора А:
В приведенном выше примере таким базисом является тройка i, j, к: векторы i и j — собственные векторы оператора проектирования Р с собственными значениями, равными единице, а к — его собственный вектор с нулевым собственным значением.
6. Пусть А: V —» V — невырожденный симметричный оператор. Тогда обратный ему оператор А -1 : V —> V также является симметричным.
Замечание:
Все собственные значения невырожденного оператора отличны от нуля. Если λ ≠ 0 — собственное значение оператора А, то 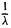
Симметричный оператор называется положительным, если для любого ненулевого элемента х из пространства V выполняется неравенство (Ах, х) > 0.
Свойства положительного оператора
- Симметричный оператор А: V —» V является положительным в том и только в том случае, когда все его собственные значения λ1…, λп положительны.
- Положительный оператор невырожден (обратим).
- Оператор, обратный положительному, также положителен.
Квадратичные формы
Пусть А = (aij) — симметричная матрица порядка п, ajj = Выражение
(1)
называется квадратичной формой переменных 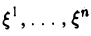
Примером квадратичной формы двух переменных х и у может служить выражение ах2 + 2bху + су2, где а, b и с — некоторые действительные числа; ее матрица
Набор чисел 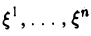
Тогда выражение (1) будет представлять собой числовую функцию аргумента х, заданную на всем пространстве V. Эту функцию принято обозначать так: A(х, х). О такой квадратичной форме
(2)
говорят, что она задана в n-мерном евклидовом пространстве
Со всякой квадратичной формой A(x, x) естественно связана симметричная билинейная форма
(3)
где 
Замечание:
Форма (3) называется билинейной, так как она линейна по каждому аргументу — и по х, и по у :
(здесь a1, a2, β1, β2 — произвольные числа).
Билинейная форма (3) называется симметричной вследствие того, что ее значение не зависит от порядка аргументов,
Вычисляя значения билинейной формы A (x, у) на базисных элементах, т. е. полагая х = еk, у = ет, получаем, что (4)
Это означает, что элементы матрицы А квадратичной формы (2) суть значения билинейной формы на элементах базиса с.
Примером билинейной формы может служить скалярное произведение векторов n-мерного координатного пространства Rn
где 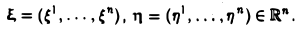
определяет квадрат длины вектора ξ.
При переходе к другому базису координаты элемента х изменяются. Меняется и матрица А = А(e) квадратичной формы.
В приложениях часто возникает необходимость приведения квадратичной формы к наиболее простому виду. Таким видом является диагональный, или нормальный вид. Будем говорить, что квадратичная форма в базисе с имеет нормальный вид, если все коэффициенты при произведениях различных координат равны нулю, т.е. аij = 0 при i ≠ j. Тогда
Матрица квадратичной формы в этом базисе имеет диагональный вид:
Теорема:
Для каждой квадратичной формы, заданной в евклидовом пространстве, можно указать (ортонормированный) базис, в котором ее матрица имеет диагональный вид.
Чтобы убедиться в справедливости этого утверждения, воспользуемся свойствами симметричного оператора. Построим линейный оператор А: V → V так, чтобы его матрица 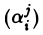
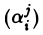
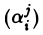
Вычислим (Aх, х). Замечая, что
вследствие ортонормированности базиса e, получаем
Тем самым, м ы установили важную связь
A(х, х) = (Aх, х) (5)
между квадратичной формой, заданной в евклидовом пространстве V, и действующим в нем симметричным оператором.
В силу симметричности построенного оператора А в евклидовом пространстве V существует ортонормированный базис f = (f1,… ,fn) состоящий из собственных элементов оператора А:
Разложим элемент х по базису f,
и вновь вычислим (Aх, х). Имеем
Отсюда в силу равенства (5) получаем, что
Тем самым, матрица A(f) исходной квадратичной формы в базисе f является диагональной:
Сам диагональный вид квадратичной формы можно (с точностью до порядка слагаемых) записать и не вычисляя элементов базиса f. Достаточно найти собственные значения линейного оператора А или, что тоже самое, собственные значения матрицы А = (aij) и выписать их с учетом кратности.
Пример:
Привести квадратичную форму
A(х, х) = 2ху + 2yz + 2xz
к диагональному виду.
Запишем матрицу квадратичной формы
и построим ее характеристический многочлен:
Приравняв полученное выражение к нулю, найдем его корни:
Построение соответствующего ортобазиxа сложнее.
Собственные векторы симметричного оператора А суть собственные векторы матрицы квадратичной формы. Найдем их.
Пусть λ = 2. Рассмотрим однородную линейную систему с матрицей
Все решения системы
пропорциональны набору (1 1 1 ) т.
Пусть λ = — I. Однородная линейная система с матрицей
сводится к одному уравнению
х + y + z = 0
и имеет два линейно независимых решения. Выберем их так, чтобы они были ортогональны: (1 -2 1 )Т, (1 0 — 1 )Т. Легко убедиться в том, что векторы с найденными координатными столбцами попарно ортогональны. Пронормируем их:
Искомый базис построен:
Замечание:
В качестве пространства V можно взять любое п-мерное евклидово пространство. Однако в задачах наиболее часто встречается координатное пространство Rn, элементами которого являются всевозможные упорядоченные наборы действительных чисел — ξ = (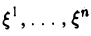
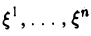

Опишем алгоритм, посредством которого для произвольной квадратичной формы, заданной в n-мерном координатном пространстве, строится базис, в котором эта квадратичная форма имеет диагональный вид.
— заданная квадратичная форма.
- Выпишем матрицу квадратичной формы
2. Построим характеристический многочлен
и найдем его корни (в силу симметричности матрицы все корни вещественны). Запишем их с учетом кратности:
3. Пусть λ — один из этих корней, кратности k. Однородная линейная система с матрицей
имеет ровно к линейно независимых решений (образующих фундаментальную систему решений). Ортонормировав ее, получим к попарно ортогональных решений единичной длины.
4. Поступая так с каждым корнем характеристического многочлена, получаем набор ровной попарно ортогональных элементов единичной длины, т. с. ортобазис f1 …, fn пространства Rn.
В построенном ортобазисе f = (f1,…,fn) заданная квадратичная форма имеет диагональный вид:
Определение:
называется положительно определенной или знакоположительной, если для любого ненулевого элемента х (или, что то же, для любого ненулевого набора 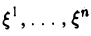
A(х, х) > 0.
Примером знакоположительной квадратичной формы может служить скалярный квадрат произвольного вектора ξ = (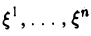
После приведения знакоположительной квадратичной формы к диагональному виду получаем
где λ1 > 0, …, λn > 0
Критерий Сильвестра (знакоположительное квадратичной формы)
Для того, чтобы квадратичная форма (6) была знакоположительной, необходимо и достаточно, чтобы все миноры ее матрицы, расположенные в левом верхнем углу, были положительны, т. е.
Метод Лагранжа
Существует еще один (простой) метод приведения квадратичной формы к диагональному виду, удобный, например, при получении ответа на вопрос, является ли квадратичная форма знакоопределенной или нет. Этот метод Лагранжа, или метод выделения полного квадрата, заключается в следующем. Пусть
— заданная квадратичная форма и a11 ≠ 0. Выпишем сначала все слагаемые, содержащие переменную ξ 1 и преобразуем их так:
Замечая, что выражение
также является квадратичной формой, но уже зависящей от меньшего числа переменных, вновь выделяем полный квадрат и т.д.
Если a11 = 0, но отлично от нуля аii(2
В результате проведенного преобразования координат, в частности, получим
И, тем самым, придем к общему случаю.
Пример:
Методом Лагранжа привести к диагональному виду квадратичную форму
A(x, х) = 2ху + 2yz + 2zx.
Введем новые координаты
Замечание:
Недостаток метола Лагранжа состоит в том, что при указанных преобразованиях координат новые координатные оси уже не являются попарно ортогональными.
Существуют и другие способы приведения квадратичной формы к диагональному виду.
Сравнивая результаты описанных выше двух способов приведения квадратичной формы 2ху + 2yz + 2zx к диагональному виду (речь идет о последних двух разобранных примерах), можно заметить, что в них соответственно одинаковы: число отрицательных коэффициентов и число положительных коэффициентов. Это совпадение не случайно, а является важным свойством квадратичных форм, называемым законом инерции:
число положительных, число отрицательных и число нулевых коэффициентов при квадратах неизвестных в диагональном виде квадратичной формы всегда одни и те же и не зависят от способа приведения квадратичной формы к этому виду.
Классификация кривых и поверхностей второго порядка
Применим описанный выше алгоритм приведения квадратичной формы к диагональному виду для классификации кривых и поверхностей второго порядка.
Кривые
Рассмотрим общее уравнение кривой второго порядка на плоскости Оху :
Построим матрицу квадратичной части ах2 + 2bху+су2:
Найдем корни λ1 и λ2 характеристического многочлена и соответствующие им собственные векторы i и j (единичные и взаимноортогональные).. Возьмем эти векторы за орты новых осей Ох и Оу (рис. 8).
Переходя к новым координатам 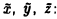
Возможны два случая: 1) λ1 • λ2 ≠ 0, 2) λ1 (или λ2 ) равно нулю.
В первом случае сдвигом точки начала отсчета
добиваемся исчезновения линейных членов
Далее, как это и делалось, рассматриваем всевозможные сочетания знаков у коэффициентов λ1, λ2 и f. В результате получаем: эллипс, гиперболу, пару пересекающихся прямых, точку, пустое множество.
Во втором случае (положим для определенности λ1 = 0, λ2 ≠ 0) сдвигом начала отсчета
приходим к уравнению
Если же d= 0,то взяв а = 0, имеем
В зависимости от знака 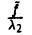
Замечание:
Операция отыскания корней характеристического многочлена квадратичной части уравнения кривой и взаимноортогональных единичных собственных векторов, описанная здесь, заменяет уничтожение произведения разноименных координат путем поворота на подходящий угол. В случае поверхностей второго порядка дело обстоит сложнее (и для того, чтобы разобраться с классификацией до конца, нужны и внимание и терпение).
Поверхности
Общее уравнение поверхности второго порядка имеет следующий вид
Упростим вид квадратичной части этого уравнения (подчеркнута), пользуясь описанным выше алгоритмом. Построим матрицу
найдем корни λ1, λ2, λз характеристического многочлена
и соответствующие им собственные векторы i, J, k так, чтобы они образовывали ортонормированную тройку (это всегда возможно). Возьмем векторы i, J и k за орты новых координатных осей Ox, Ox, Oz. Производя замену координат, получим (*)
Возможны три случая:
(I) Все три корня λ1, λ2, λ3 отличны от нуля. Путем сдвига начала
уравнение (*) поверхности приводится к следующему виду
имеют один и тот же знак, противоположный знаку 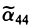
получаем уравнение эллипсоида
β ) Знаки λ1 и λ2 противоположны знаку 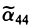
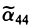
получаем уравнение однополостного гиперболоида
γ ) Знаки λ1 и λ2 совпадают со знаком 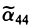
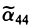
получаем уравнение двуполостного гиперболоида
б. 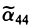
а) Если λ1, λ2 и λз имеют один и тот же знак, то получаем точку (0, 0, 0).
β) Если одно из λ, имеет знак, противоположный знаку двух других, то получаем уравнение конуса второго порядка
(II) Ровно один корень равен нулю (для определенности λз = 0). Полагая
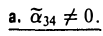
получаем уравнение вида
а) Если λ1 и λ2 — одного знака, то, полагая
(можно считать, что знак 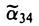
β) Если λ1 и λ2 имеют противоположные знаки, то, положив
получим уравнение гиперболического параболоида
б. 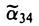
Классификация поверхностей с уравнениями такого типа приводится в таблице.
Замечание:
Отсутствие третьей координаты (точнее, ее неявное присутствие) приводит к цилиндрическим поверхностям, направляющими которых являются кривые второго порядка, лежащие в плоскости Z = 0 и имеющие уравнения вила
(III) Ровно два корня равны нулю (для определенности λ2 = λ3 = 0). Преобразованием координат
приходим к уравнению
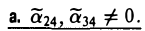
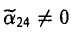
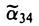
уравнение поверхности приводится к следующему виду
Замечание:
Преобразование координат, упрощающее вид уравнения, выбирается так, чтобы новая координатная система вновь была прямоугольной декартовой.
Сдвигом начала координат
получаем уравнение параболического цилиндра
описывает либо пару параллельных плоскостей ( λ1 • 
Дополнение к линейным отображениям






Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института