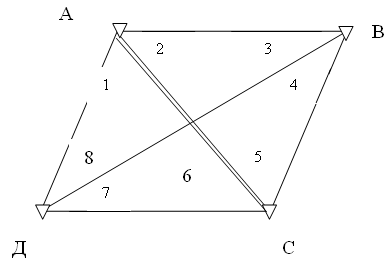
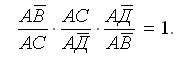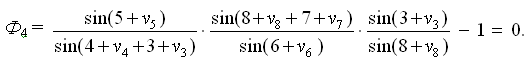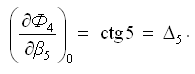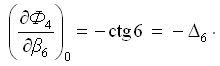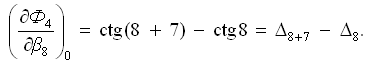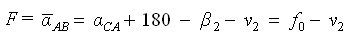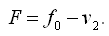Что такое геодезический четырехугольник (7 видео)

Уравнивание геодезического четырехугольника коррелатным способом

Для определения координат пунктов В и Д в геодезическом четырехугольнике (рис. 2) измерено равноточно (р_i = 1) восемь углов между сторонами и диагоналями. Результаты измерений помещены в табл. 5.

Рис. 2. Геодезический четырехугольник

№ углов	Измеренные углы β_i	№ углов	Измеренные углы β_i
77°35′ 46,3″	36°00′ 05,7″
57° 00′ 57,0″	46° 29′ 49,3″
27° 22′ 57,6″	37° 54′ 10,8″
59° 35′ 57,7″	18° 00′ 15,7″

Определим число независимых условных уравнений.

Число необходимых измерений в линейно-угловой сети равно удвоенному числу вновь определяемых пунктов, t = 2 · 2 = 4. Число избыточных измерений

r = n — t = 8 — 4 = 4.

В геодезическом четырехугольнике имеют место четыре независимых условных уравнения, 3 — условных уравнения фигур и 1 — полюсное.

Составим условные уравнения связи.

Условное уравнение фигур: сумма углов плоского треугольника после уравнивания минус 180° равна нулю.

Обозначим β_i = i. Для трех треугольников, например, ΔАВС, ΔАДС, ΔАВД условные уравнения фигур будут иметь вид:

Полюсное условное уравнение: отношение сторон, сходящихся в одной точке (полюсе), после уравнивания равно единице. Если полюс — точка А, то

По теореме синусов, отношение сторон заменяют отношением синусов противолежащих углов:

Составим условные уравнения поправок.

Условные уравнения фигур имеют линейный вид. Для перехода к условным уравнениям поправок следует вычислить невязки, которые равны суммам измеренных углов в треугольнике минус 180°.

Полюсное условное уравнение связи приводят к линейному виду разложением в ряд Тейлора

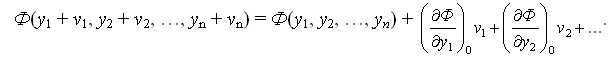
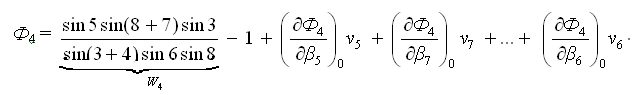
Частная производная функции Ф₄ по аргументу β₅ (углу числителя):

Частная производная функции Ф₄ по аргументу β₆ (углу знаменателя):

Частная производная функции Ф₄ по аргументу β₈ (углу числителя и знаменателя):

С учетом размерности поправок и невязки полюсное условное уравнение поправок имеет вид:

Умножив на ρ″, получим

Определение коэффициентов Δ_i и невязки w″₄ полюсного условного уравнения выполним на ПК по программе Polus.exe. Исходной информацией к программе являются углы числителя и знаменателя полюсного условного уравнения (табл. 6).

.	Числитель	.	.	Знаменатель	.
№ углов	β_i	Δ_i	№ углов	β_i	Δ_i
36°00′ 05,7″	1,38	3+4	86°58′ 55,3″	0,05
8+7	55° 54′ 26, 5″	0,68	46° 29′ 49,3″	0,95
27° 22′ 57,6″	1,93	18° 00′ 15,7″	3,08

Полюсное условное уравнение поправок принимает вид:

Составим весовую функцию.

— дирекционный угол стороны АВ, вычисленный по результатам уравнивания.

Итак, получена следующая система условных уравнений поправок:

(24)

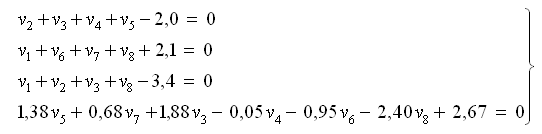
Коэффициенты условных уравнений и функции

№ измерения	a	b	c	d	f	ν
.
-1	.
+1.88	.
-0.05	.
+1.38	.
-0.95	.
+0.68	.
-2.40	.

и весовая функция:

Коэффициенты условных уравнений и функции поместим в табл. 7.

Дальнейшее решение задачи выполните на ПК по программе KORREL.EXE. Таблицу коэффициентов условных уравнений вводите по столбцам.

Выпишите с экрана:

1. Значения поправок к результатам измерений в столбец ν табл. 7.

2. Среднюю квадратическую ошибку измерения — m.

3. Обратный вес 1/P_F и среднюю квадратическую ошибку функции — m_F.

Вычислите уравненные значения углов 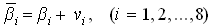и сделайте контроль уравнивания.

Дата добавления: 2016-06-24 ; просмотров: 3714 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Содержание

Классификация основных способов уравнивания
Основные геометрические условия, возникающие в построениях
Планово-высотная основа мостового перехода
🌟 Видео

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Классификация основных способов уравнивания

Способы уравнивания результатов измерений в геодезических построениях разделяют на два основных вида: строгие способы и нестрогие способы уравнивания.

К строгим способам уравнивания относятся коррелатный и параметрический способы. Следует отметить, что оба названных способа дают идентичные результаты. Эти способы позволяют полностью реализовать в той или иной схеме метод наименьших квадратов практически для любых по сложности построений.

В некоторых случаях при уравнивании геодезических построений сравнительно малой точности применяют упрощенные способы уравнивания, которые относят к нестрогим способам. Например, в любом полигонометрическом ходе число избыточных измерений всегда равно трем. Очевидно, что число избыточных измерений практически намного меньше необходимых. Это приводит к тому, что при уравнивании не будет достигаться заметного повышения точности. Для одиночных полигонометрических ходов и даже для систем полигонометрических ходов с одной или двумя узловыми точками можно рекомендовать способ раздельного уравнивания. В частности, способ раздельного уравнивания был рассмотрен выше при обработке разомкнутого или замкнутого теодолитного хода: сначала выполнялось уравнивание горизонтальных углов (дирекци- онных углов), а затем — уравнивание приращений координат (координат). В полигонометрических сетях малой точности, содержащих не более 3 — 4 узловых пунктов, используют способ эквивалентной замены. Если полигонометрическая или нивелирная сеть содержит большое число исходных пунктов, то наиболее эффективно применять способ последовательных приближений. Нивелирные сети, состоящие из полигонов, при пониженных требованиях точности уравнивают, как правило, способом полигонов В.В. Попова. О всех указанных здесь способах пойдет речь в последующих параграфах этой главы.

Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Основные геометрические условия, возникающие в построениях

Если геодезические построения состоят только из необходимых исходных данных, то такое построение (сеть) называется свободным (свободной) и уравниванию не подлежит. При наличии избыточных измерений построение (сеть) называется несвободным (несвободной), и в нем (ней) может быть выполнено уравнивание при наличии невязок, определяемых выполнением тех или иных условий в геометрических связях.

При уравнивании геодезических построений необходимо правильно определить число и видт. н. условных уравнений. В связи с этим должны быть составлены только необходимые условия, не больше. В противном случае система уравнений не может быть разрешима. Меньшее же число условий вообще исключает решение задачи уравнивания, поскольку хотя бы одна из невязок будет ис- ключена из рассмотрения._

Далее приведем основные геометрические условия, которые могут определять вид того или иного условного уравнения связи в геодезическом построении.

134.1. Условие фигуры

В замкнутой фигуре, имеющей п вершин, сумма уравненных значений измеренных углов должна быть равна 180° (л ± 2), т. е.;

где знак «плюс» в круглых скобках — для внешних, знак «минус» — для внутренних углов; р’ — исправленные (уравненные) углы.

В этом случае условное уравнение поправок имеет вид:

где Р₍. — измеренные углы.

Поскольку два последних слагаемых образуют т. н. угловую невязку W, т. е.

то выражение (14.14) можно представить в виде:

Выражение (14.13) и является геометрическим соотношением (уравнением связи) для условия фигуры.

Если в той же замкнутой фигуре углы заменить разностями направлений (т. е. отсчетов по горизонтальному кругу теодолита), то получается условное уравнение поправок для измеренных направлений:

В формуле (14.17) точкой стояния является точка i.

134.2. Условие горизонта

Сумма уравненных значений неперекрывающихся углов, измеренных независимо (т. е. отдельно друг от друга) вокруг одной вершины (рис. 14.1), должна быть равна 360°, т. е.;

Рис. 14.1. Условие горизонта

Условное уравнение поправок горизонта имеет вид (14.16), где

для измеренных углов Р₍.

Для измеренных направлений условие горизонта не возникает, поскольку в этом случае всегда сумма углов, вычисленных по разностям направлений, будет равна 360° (зависимые измерения). Если же в измеренные углы ввести поправки, то и для направлений может возникнуть условие горизонта. Поэтому условные уравнения поправок со свободным членом, равным нулю, необходимо включать в уравнивание.

134.3. Условие суммы углов

Рис. 14.2. Условие суммы углов

Для измеренных в одной вершине углов Р₂, р_з и Р₄ (рис. 14.2) должно соблюдаться следующее геометрическое условие:

В этом случае условное уравнение поправок будет иметь вид:

где Wp — свободный член уравнения, определяемый суммой

134.4. Условие дирекционных углов

Для решения геодезического построения (при определении координат его точек) необходимо знать исходный дирекционный угол одной из его сторон. Если же в сети известны дирекционные углы других сторон, то каждый из них образует одно условие. Например, если в сети (рис. 14.3) известны дирекционные углы оц, а₂ и а₃, то геометрическое условие дирекционных углов запишется в виде:

Рис. 14.3. Условие дирекционных углов

Условные уравнения поправок в этом случае определяются выражениями:

В выражениях (14.23) — (14.25) принимается во внимание, что все дирекционные углы были измерены (они могут быть и вычислены по значениям координат, имеющих известные погрешности), т. е. содержат погрешности и подлежат уравниванию. Чаще всего дирекционные углы принимают исходными, т. е. содержащими погрешности весьма малые (ничтожные) по сравнению с погрешностями измеренных углов. В этом случае выражения (14.25) запишутся в виде:

(а₀ — исходные дирекционные углы).
134.5. Условие сторон

Предположим, что в фигуре (рис. 14.4) измерены все углы р и стороны s, и s₂. Между сторонами, из решения треугольников, существует следующее соотношение:

Это равенство можно представить в виде нелинейной функции

Приведем нелинейную функцию (14.30) к линейному виду, разложив ее в ряд Тейлора и ограничиваясь только первыми членами разложения. Получим:

Найдем частные производные:

где s₂° — вычисленное по формуле (14.29) значение s₂ по измеренным аргументам s,, р₁₍ р₃, Р₄, Р₅. С учетом (14.32)

Аналогично можно записать выражения для р₃, р₄ и р₅:

Введем следующие обозначения:

Умножим выражение (14.31) на 1 / s₂° и подставим в него значения частных производных (14.32) — (14.34). Уравнение поправок будет иметь вид:

где W_s = 2 ₀ 2 р —относительная погрешность стороны s; 8, = ctg(3,;

р — угловая мера радиана.

Если стороны Sj и s₂являются базисами (исходными), то поправки для них будут равны нулю. В этом случае условное уравнение поправок исходных сторон (базисов) упрощается:

где W_s = 2 02 р; s₀₂ — базис.

Рис. 14.4. Условие сторон

134.G. Условие полюса

Условие полюса возникает в такой фигуре (рис. 14.5), в которой можно образовать замкнутый ряд треугольников, начинающихся и заканчивающихся на одной и той же стороне (например, центральная система, геодезический четырехугольник, веер). Если эту сторону принять за исходную (базис), то из решения треугольников можно получить эту сторону вторично.

Например, для центральной системы рис. 14.5 можно записать,

что

Условное уравнение поправок данного полюса с учетом введенных выше обозначений (14.37) имеет вид:

Рис. 14.5. Условие полюса

132.7. Условие координат

В геодезическом построении каждый избыточный исходный пункт обусловливает два условных уравнения координат — уравнения абсцисс (х) и уравнения ординат (у).

Предположим, что измерения выполнены в цепочке треугольников триангуляции (рис. 14.6), заканчивающейся на избыточном пункте 5. Наметим ходовую линию, проходящую через вершины промежуточных углов г),: 1 — 3 — 4 — 5. В этом случае координатные условные уравнения (абсцисс и ординат) будут иметь вид:

При решении треугольников триангуляции стороны и дирекци- онные углы определяют от исходных сторон s₀ (базиса) и исходного дирекционного угла а₀:

Рис. 14.6. Условие координат

Представим уравнения (14.41) через поправки в углы в линейной форме:

Свободными членами W_x и W_y в уравнениях (14.43) являются приближенные значения искомых функций (14.41), вычисленные по измеренным горизонтальным углам с использованием равенств

Из уравнений (14.41) найдем частные производные (коэффициенты условных уравнений поправок) и подставим их в уравнения

(14.43) . При этом поправки углов выражаются в секундах, свободные члены — в дециметрах, а разности координат — в километрах. Получим условные уравнения поправок:
— для координатх (при уравнивании углов):

— для координат у (при уравнивании углов):

Здесь х_пиу_п — координаты последнего пункта (для рис. 14.6 х_п = х₅, Уп = 7s) > x i и 7, — координаты текущего пункта i ходовой линии, проходящей через вершины промежуточных углов ц,; v_p, и v_yi — поправки связующих углов Р и у (угол у лежит против исходной стороны треугольника); v_4f — поправки промежуточных углов r_j (записываются со знаком «плюс» для левых по ходу углов, со знаком «минус» —для правых по ходу углов).

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Планово-высотная основа мостового перехода

Геодезическая разбивочная сеть мостового перехода строится в соответствии с основным принципом геодезических построений — переходом от общего к частному. От всеохватывающих точных построений (на всём строительном объекте, мостовом переходе) последовательно производят локальные, частные построения (разбивки опор, конструкций). Таким образом, разбивочная сеть является общей основой разбивки моста, она должна обеспечить контроль разбивочных работ на всех стадиях строительства. Поэтому в процессе её проектирования принимают во внимание многие обстоятельства, способствующие успешной реализации строительства.

Планово-высотная сеть мостового перехода должна быть максимально удобной для производства разбивочных работ и контроля центров опор. Пункты сети должны располагаться в местах, обеспечивающих их максимальную сохранность и незыблемость планово-высотного положения. Располагают пункты с учётом технологии строительства и его организации.

В зависимости от конкретных условий строительства и от наличия соответствующих геодезических приборов плановая разбивочная сеть мостового перехода может быть выполнена в виде триангуляционных, линейно-угловых построений или полигонометрии. Сегодня всё чаще схемы разбивочных сетей реализуются на основе спутниковых определений и в комбинации с традиционными технологиями. Иногда в качестве геодезической разбивочной основы принимают закреплённую ось моста и параллельные ей створы, если разбивка опор моста может быть выполнена но оси сооружения светодальномером или электронным тахеометром.

Разбивочную сеть создают в частной системе координат. Одну из координатных осей (чаще ось х) совмещают с осью мостового перехода. Координаты одного из пунктов, лежащих на этой оси, задают исходя из условия положительности координат всех пунктов. Предельная ошибка положения пунктов разбивочной сети относительно исходного равна 6 мм. Для подавляющего большинства случаев это требование является несколько завышенным. Поэтому считается целесообразным рассчитывать точность разбивочной сети в каждом конкретном случае, исходя из требований к конечным результатам.

Специфической особенностью мостовых разбивочных сетей является то, что оцениваемой стороной всегда является сторона, совпадающая с осью мостового перехода. Для больших мостов требуется, чтобы предельная ошибка определения длины мостового перехода не превышала величины

где /, — длина пролёта с номером i, см; п — число пролётов моста.

Мостовая триангуляция. Этот вид геодезических построений, весьма популярный во времена, когда отсутствовали спутниковые определения, а высокоточные линейные измерения производились очень сложными и дорогостоящими способами, сегодня потерял своё значение, уступив место современным электронным методам и средствам высокоточных измерений и координатных определений.

Типовой фигурой мостовой триангуляции является сдвоенный геодезический четырёхугольник, рис. 11.6, а и геодезический четырёхугольник, Ь.

Наиболее удобным является четырёхугольник с продвигом, равным ‘А (отношение стороны на берегу к стороне, направленной перпендикулярно потоку). Такая форма геодезического четырёхугольника выбирается потому, что основным способом разбивки в отсутствие электронных тахеометров является прямая угловая засечка. Для реализации этого способа с максимально возможной точностью необходимо, чтобы углы засечки в центре опоры составляли около 90°, т. е. чтобы береговые стороны четырёхугольника равнялись примерно половине длины мостового перехода. С такой формой образующие фигуру треугольники будут иметь острые углы при диагоналях около 27°, что приводит к существенному

Схемы мостовой триангуляции

возрастанию ошибок геометрической связи треугольников (обратные веса).

Рис. 11.7. Четырёхугольник с диагоналями

Мостовая триангуляция не является оптимальным построением также в связи с тем, что часть сторон фигур проходит в рефракционно опасных зонах. Кроме того, на результаты угловых измерений существенное влияние оказывают ошибки центрировки и редукции.

Мостовые сети являются сравнительно простыми геодезическими построениями и чаще всего уравниваются упрощенными методами. В этом случае сначала уравнивают условия фигур, а затем — полюса.

На рис. 11.7 изображён геодезический четырёхугольник. Для него число независимых условий фигур будет три, если измерены все восемь углов. Кроме того, в этом четырёхугольнике возникает ещё одно условие — условие полюса. Это условие возникает из требования, чтобы диагональ DA прошла через точку Л (что не обеспечивают три условия фигур).

Условия фигур будут выглядеть так:

Приняв за полюс точку пересечения диагоналей, можно составить условие полюса:

После известных преобразований, переходя к условным уравнениям поправок, получим:

Для полюсного условия будем иметь:

Решая уравнения (11.3) получим первичные поправки в углы:

Вторичные поправки в углы находят, решая полюсное уравнение поправок. При этом ставят условие, чтобы вторичные поправки были равны друг другу и имели противоположные знаки для числителя и знаменателя уравнения (11.4), иначе

Для этих условий вторичные поправки вычисляются по формуле

В этой формуле а и /? — приращения логарифмов синусов углов при изменении величины угла на одну секунду.

Описанный упрощённый метод уравнивания геодезического четырёхугольника практически приводит к тем же результатам, что и строгое уравнивание.

Если разбивочная сеть мостового перехода выполнена из двух спаренных четырёхугольников с двумя базисами (рис. 11.6, а), то эту сеть уравнивают за условия фигур, затем каждый четырёхугольник уравнивают независимо за условия полюса и вычисляют два значения мостового перехода, из которых берут среднее.

Линейно-угловая сеть. В связи с широким внедрением в геодезическое производство точных электронных тахеометров для разбивки мостовых переходов всё чаще стали применяться специальные линейно-угловые построения. Типовой фигурой таких сетей является так называемый базовый треугольник 1.2.3.4., в котором измерены четыре стороны и углы при вершинах (рис. 11.8). Береговые стороны и направления в фигурах не измеряются. Обычно строят сдвоенный базовый треугольник: один выше, а другой ниже по течению. Средняя сторона 1-2 при этом совмещается с осью моста, стороны 3-4 и 5-6 служат базисами разбивки.

Такие сети обладают рядом достоинств. Отсутствие направлений вдоль берегов позволяет измерять углы в примерно одинаковых внешних условиях и уменьшает влияние боковой рефракции. Взаимная видимость между пунктами сети обеспечивается без постройки высоких знаков.

В базовом треугольнике возникает три условия: фигур, сторон и проекций.

Условие фигур состоит в равенстве углов в пересекающихся диагоналях:

Рис. 11.8. Сеть из базовых треугольников

Уравнение поправок при этом будет иметь вид: где w_p = Д+Д-Д-Д.

Условие сторон заключается в том, что общая для двух смежных треугольников неизмеренная сторона, вычисленная по измеренным элементам этих треугольников, должна быть одинаковой. Например, для стороны 2-4 из треугольников 2.4.3 и 2.4.1 имеем

или условные уравнения поправок где

Скобками (1) или (s,) обозначены поправки в углы и стороны.

Условие проекций заключается в том, что сумма проекций сторон базового треугольника на ось мостового перехода равна нулю:

где

Условные уравнения решают при условии

где рр и p_s — веса измеренных углов и сторон при рр =1 и p_s = m 2 _fj jт].

Исследования показывают [27], что в сетях из базовых треугольников ошибка уравненного дирекционного угла стороны равна ошибке угловых измерений т_а= тр, а средняя квадратичная ошибка уравненной стороны практически не зависит от размеров и формы сети и примерно на 15% меньше ошибки линейных измерений: m_syp=0,85m_stmi.

Ошибки координат и ошибки положения конечных пунктов базиса разбивки увеличиваются с увеличением длины мостового перехода и продвига сети. Ошибки абсцисс (но оси моста) при этом возрастают быстрее, чем ошибки ординат.

Базовые треугольники связаны между собой одной общей стороной, поэтому полученными формулами можно пользоваться при оценке типовой сети из двух фигур.

Спутниковые сети на мостовых переходах. В качестве базовой станции выбирают ближайший пункт или несколько пунктов ГГС. Надёжно закрепив точки А и В (рис. 11.9, а), определяют их координаты как роверных пунктов относительно базовой (референцной) станции. Контроль координатных определений можно выполнить прямым промером расстояния АВ электронным тахеометром. Однако этого может оказаться недостаточным. В таких случаях при построении каркасной сети из спутниковых определений действующие нормативные документы (СП 47.13330 2012) требуют построения 3 спутниковых пунктов с взаимной видимостью, что позволяет произвести контроль определений координат прямым измерением расстояний между пунктами, а также горизонтальных углов фигуры.

При возведении средних и малых мостов двух пунктов (А и В) вполне достаточно для выполнения разбивок опор и производства других геодезических работ. Однако ситуация на строительной площадке, наличие машин и механизмов чаще всего не позволяют выполнять прямые промеры в створе линии АВ. Поэтому для удобства производства разбивочных работ на берегах строят дополнительные геодезические знаки с таким расчётом, чтобы с береговых пунктов (Си А рис. 11.9, а) визирные линии для точек на оси моста пересекались под углом, близким 90°.

Точность таких построений диктуется нормами точности (формула 11.2), а погрешности координат точек сети не должны превышать 6 мм.

Эти требования к расположению пунктов разбивочной основы продиктованы не только условиями производства разбивок способом прямой угловой засечки, но также удобствами реализации контрольных измерений с береговых пунктов на точки, расположенные на оси сооружения.

Полигонометрические сети. При строительстве моста или путепровода на сравнительно сухой пойме или суходоле разбивочная сеть может быть создана в виде полигонов. Все пункты в такой сети являются узлами. При построении полигонометрии активно используются электронные тахеометры, позволяющие производить линейные измерения с высокой точностью (2 — 3 мм). Углы в ходах измеряют с погрешностями не хуже 2 — 3″.

На больших мостовых переходах разбивочная основа может быть построена из сочетания спутниковой сети и полигонометрических ходов. При этом пункты спутниковой сети располагают в качестве магистрального хода вдоль оси трассы. Сгущение сети на мостовом переходе производят полигонометрическими ходами (рис. 11.9, Ь).

Разбивочные сети мостовых переходов уравнивают строгими способами. После уравнивания спутниковой сети координаты пунктов перевычисляют в стро-

Разбивочные сети: а — спутниковая;

ительную (частную) систему координат, совместив ось X с направлением ЛВ мостового перехода.

Высотную геодезическую сеть на мостовом переходе создают ещё в период изысканий для обеспечения высотами топографических съёмок, для производства разбивочных работ и контрольных наблюдений в период строительства и эксплуатации моста. Грунтовые реперы, заложенные на стадии изысканий, служат исходной основой для передачи высот на опоры и устои моста. Погрешности высот постоянных реперов не должны превышать 3 мм, для временных реперов — 5 мм. Эго требование обеспечивается нивелированием III класса.

Реперы, расположенные на противоположных берегах реки, должны иметь отметки в единой системе высот, а погрешности их взаимного высотного положения не должны превышать приведённых выше значений. Для передачи отметок на пункты высотной основы и строительные конструкции применяют три основных метода: геометрического, тригонометрического и гидростатического нивелирования. Однако последний метод не получил широкого распространения из-за его трудоёмкости, хотя зимой по льду, с применениями незамерзающих жидкостей в качестве наполнителей трубопровода он вполне может конкурировать с двумя другими методами.

Зимой отметки через реку можно передавать непосредственным нивелированием по льду. Для этого предварительно в лёд вмораживают деревянные столбики для установки реек. Работы выполняют в периоды наименьших суточных подвижек льда по возможности в кратчайшие сроки.

В летнее и осеннее время в зависимости от характера и ширины водной преграды для передачи высотных отметок с одного берега на другой могут применяться разнообразные схемы и методы геометрического нивелирования. Основные из них рассмотрены в «Инструкции по нивелированию I, II, III и IV классов. ГУГК СССР. — М.: Недра, 1990, — 167 с.».

При ширине реки 300 — 500 м для сокращения расстояний до реек используют имеющиеся острова, отмели или забивают в дно на середине реки сваю для установки реек. На реечную точку на свае передают отметку с каждого берега при нескольких установках нивелира. Работы выполняют синхронно при одновременной установке трёх реек — на свае и двух реперах.

Рис. 11.10. Передача отметки через водное препятствие

11ри ширине реки до 300 м распространение получил метод двойного геометрического нивелирования, сущность которого заключается в следующем.

На обоих берегах примерно на одной высоте закладывают реперы 1 и 2, рис. 11.10. Для ослабления влияния рефракции нивелирование целесообразно выполнять одновременно двумя нивелирами с противоположных берегов, меняя затем их местами.

Нивелиры I, и /, устанавливают на одинаковом расстоянии от реперов так, чтобы d, = d₃ и d₂ = d₄.

Приведя нивелиры в рабочее положение, производят отсчёты по ближней рейке и по рейке на противоположном берегу, что составляет приём. Среднее значение превышений в приёме будет свободно от погрешностей, вызванных наличием угла i. Количество приёмов устанавливают не менее двух. Расхождение между приёмами не должно превышать 10 мм. Затем нивелиры меняют местами. За окончательное значение превышения между реперами берут среднее из измерений.

При большой ширине реки отсчёты по дальней рейке непосредственно не берут. По сигналу наблюдателя но рейке перемещают специальный щиток с прорезью в виде окошечка. В момент совмещения прорези с горизонтальной нитыо зрительной трубы нивелира через окошечко производят отсчёт по рейке.

Работы по передаче отметок через водные преграды выполняются особенно тщательно. Перед наблюдениями детально исследуют нивелиры и рейки, определяют и исправляют угол i, защищают нивелиры от прямого попадания солнечных лучей. Наблюдения стремятся выполнять в кратчайшие сроки.

Отечественный и зарубежный опыт показывает, что передача отметок через реку шириной около 1000 м описанным способом может быть выполнена с погрешностью около 3-5 мм.

С широким внедрением в практику инженерно-геодезических работ электронных тахеометров для передачи отметок через водные пространства всё чаще используют метод тригонометрического нивелирования.

Естественно, процесс передачи высот тригонометрическим нивелированием в сравнении с приведёнными выше методами представляется более привлекательным по своей простоте и доступности. Однако метод не так прост, как это может показаться на первый взгляд. Все проблемы метода тригонометрического нивелирования заключаются в неоднозначности коэффициента земной рафракции, под которым понимают отношение радиуса R земного эллипсоида к радиусу R, кривизны визирного луча на измеряемой дистанции. При этом предполагается, что обе кривые располагаются в одной вертикальной плоскости и траектория визирного луча представляет собой дугу окружности радиуса R,. Понятно, что это гипотетические допущения, а в действительности путь луча в атмосфере будет определяться случайными процессами распределения температурных полей, плотности и других показателей состояния атмосферы.

Рассмотрим способ тригонометрического нивелирования с использованием электронного тахеометра при передаче высот через водные преграды.

Ранее нами выведена формула (2.32) одностороннего тригонометрического нивелирования, которую применительно к рис. 11.11 и с учётом (2.36) можно записать несколько расширено:

Здесь S_A2 — длина линии А-2, измеренная электронным тахеометром; v_A2 — угол наклона этой линии к горизонту; i_A — высота прибора над репером 1; V₂ — высота отражателя на репере 2; R — средний радиус Земли; к, — коэффициент земной рефракции. Последнее слагаемое формулы (11.15) учитывает не только влияние искривления луча из-за рефракции, но также влияние кривизны Земли

на результаты нивелирования, это член

Превышение между обозначенными точками можно измерить в обратном направлении:

В этих уравнениях первый член S ? sin v = h представляет собой превышение, вычисляемое компьютером тахеометра но непосредственно измеренному углу v и расстоянию S.

В случае двустороннего тригонометрического нивелирования превышения h,₂ и h_2l должны быть равны по абсолютной величине и противоположны по знаку и, очевидно, среднее из прямого и обратного превышений определится h ₉ — h

по формуле h_cp — 1,2 ^ 2,1 . Принимая во внимание вышесказанное, для среднего значения превышения получим

Рис. 11.11. Нивелирование через реку

Из этой формулы видно, что при равных значениях коэффициента рефракции (к₂ = к,) среднее из прямого и обратного превышений должно быть свободно от влияния рефракции. Поэтому схему измерений и собственно наблюдения следует организовать таким образом, чтобы поставленные условия были реализованы. Так, прямые и обратные измерения должны выполняться одновременно двумя тахеометрами. Путь луча прямого измерения должен проходить вблизи пути распространения луча обратного измерения. Пути лучей должны быть приблизительно равны.

Рис. 11.12. Схема тригонометрического нивелирования

На рис. 11.12 приведена схема расположения приборов по отношению к реперам 1 и 2 высотной сети мостового перехода. Приборы располагают в непосредственной близи от реперов так, чтобы не перекрывать отражатели, установленные на реперах и на равном расстоянии от них (2-3 м).

На первом этапе после установки приборов и приведения их в рабочее положение на реперы устанавливают шашечные рейки и, приведя трубы приборов на отсчёт по вертикальному кругу, равный 0° (или 90°), берут отсчёт по рейке. Для прибора в точке Л это отсчёт по рейке в точке 1. Для тахеометра в точке В — отсчёт по рейке в точке 2. Эти отсчёты суть высоты приборов в точках Л и В над соответствующими реперами, рис. 11.11.

На втором этапе над реперами центрируют отражатели и тщательно измеряют высоты центров симметрии призм над реперами — это высоты визирных целей V, и V₂.

Далее выполняются непосредственные измерения, т. е. зрительная труба тахеометра наводится на середину отражателя, расположенного на противоположном берегу и включаются измерения. Таких наведений и измерений выполняют 3-5. После чего приборы меняют местами и измерения повторяют. Обязательным является измерение и введение параметров атмосферы: давления и температуры.

При спутниковых определениях наряду с пространственными координатами пунктов магистральных ходов определяются и высоты этих пунктов. Это геодезические высоты. Для перехода к нормальным высотам необходимо знать аномалии высот в районе работ. Однако точность спутниковых определений высот сегодня несколько ниже приведённых ранее требований к построению высотных сетей мостового перехода, и, тем ни менее, способ передачи высот методами ГНСС может оказаться единственно возможным при построении мостов значительной протяжённости.