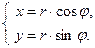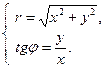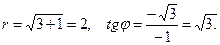Неверно введено число.
Вектор не должен быть нуль-вектором.
Взаимное расположение двух векторов
Введите координаты векторов:
| a | = | ( , ) |
| b | = | ( , ) |
| a | = | ( , , ) |
| b | = | ( , , ) |
Количество знаков после разделителя дроби в числах:
Теория
Два вектора называются коллинеарными, если они лежат на одной и той же прямой или на параллельных прямых
Нуль-вектор считается коллинеарным любому вектору.
Условие коллинеарности двух векторов. Для того чтобы векторы a и b, заданные координатами, были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны. Т.е. существует такое действительное число λ, что
Условие перпендикулярности двух векторов. Для того чтобы векторы a и b были перпендикулярны, необходимо и достаточно, чтобы их склярное произведение было равно нулю.
Видео:Разложение вектора по базису. 9 класс.Скачать

Векторы на плоскости и в пространстве — основные определения
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Определение вектора
В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.
Для начала дадим определение:
Вектор – это направленный отрезок прямой.
Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.
В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a → . Если известны граничные точки вектора – его начало и конец, к примеру A и B , то вектор обозначается так A B → .
Видео:Найдите разложение вектора по векторам (базису)Скачать

Нулевой вектор
Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.
Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.
Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Длина вектора
Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.
Длину вектора A B → принято обозначать так A B → .
Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.
Видео:Как разложить вектор по базису - bezbotvyСкачать

Коллинеарность векторов
Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.
Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.
Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.
Видео:Скалярное произведение векторов. 9 класс.Скачать

Направление векторов
Сонаправленными векторами называют два коллинеарных вектора a → и b → , у которых направления совпадают, такие векторы обозначаются так a → ↑ ↑ b → .
Противоположно направленными векторами называются два коллинеарных вектора a → и b → , у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a → ↑ ↓ b → .
Считается, что нулевой вектор является сонаправленым к любым другим векторам.
Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Равные и противоположные векторы
Равными называются сонаправленные вектора, у которых длины равны.
Противопожными называются противоположно направленные вектора, у которых их длины равны.
Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.
Пусть заданы два произвольных вектора на плоскости или в пространстве a → и b → . Отложим от некоторой точки O плоскости или пространства векторы O A → = a → и O B → = b → . Лучи OA и OB образуют угол ∠ A O B = φ .
Видео:2 42 Ортогональность векторовСкачать

Углы между векторами
Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .
Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.
Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).
Видео:89. Разложение вектора по двум неколлинеарным векторамСкачать

Определение взаимной ориентации векторов в пространстве
Читайте также:
|
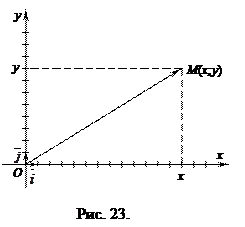 |
Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми – осями, на каждой из которых выбрано положительное направление и задан единичный (масштабный) отрезок. Единицу масштаба берут обычно одинаковой для обеих осей. Эти оси называют осями координат, точку их пересечения О – началом координат. Одну из осей называют осью абсцисс (осью Оx), другую – осью ординат (осью Оy) (рис. 23).
На рисунках ось абсцисс обычно располагают горизонтально и направленной слева направо, а ось ординат − вертикально и направленной снизу вверх. Оси координат делят
плоскость на четыре области – четверти (или квадранты).
Единичные векторы осей обозначают 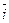
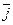
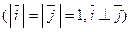
Систему координат обозначают Oxy (или 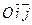
Рассмотрим произвольную точку М плоскости Oxy. Вектор 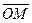
Координатами точки М в системе координат Oxy ( 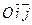
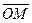
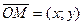
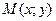
Эти два числа х и у полностью определяют положение точки на плоскости, а именно: каждой паре чисел х и у соответствует единственная точка М плоскости, и наоборот.
Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой О, называемой полюсом, лучом Оp,
называемой полярной осью, и единичным вектором 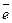
Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием r от полюса О и углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки) (см. рис. 24).
Числа r и φ называются полярными координатами точки М, пишут 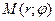
Для построения всех точек плоскости достаточно полярный угол φ ограничить промежутком 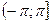
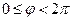
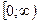
Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Оху, а полярную ось с положительной полуосью Ох. Пусть х и у – прямоугольные координаты точки М, а r и φ – ее полярные координаты.
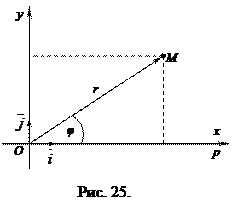 |
Из рисунка 25 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:
Полярные же координаты точки М выражаются через ее декартовы координаты (тот же рисунок) такими формулами:
Определяя величину φ, следует установить (по знакам х и у) четверть, в которой лежит искомый угол, и учитывать, что 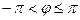
Пример 9.1. Дана точка 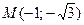


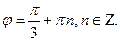
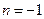
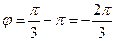
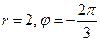
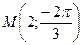
Дата добавления: 2015-01-15 ; просмотров: 11 ; Нарушение авторских прав
🎥 Видео
Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

А ТЫ УЖЕ РАЗОБРАЛСЯ С УМНОЖЕНИЕМ ВЕКТОРОВ? ЧАСТЬ II #математика #егэ #огэ #формулы #профильныйегэСкачать

Лекция 26. Взаимное расположение двух плоскостей.Скачать

ТЕСТ НА ЭРУДИЦИЮ и кругозор: МНОГО УМНЫХ ВОПРОСОВ, ответы знает не каждый. #насколькотыумный #тестСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Скалярное произведение векторов через координаты. 9 класс.Скачать

Координаты вектора в пространстве. 11 класс.Скачать

➡️ КАК ВЫЧИТАТЬ ВЕКТОРЫ?Скачать

A.7.3 Проекции векторов. А вот и датасайнс!Скачать






 ,
,  и
и 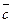 основано на следующих соображениях. Если
основано на следующих соображениях. Если 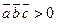 , то
, то 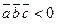 , то
, то 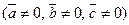 :
: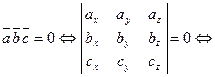 векторы
векторы 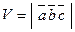 , а объем треугольной пирамиды, построенной на этих же векторах, равен
, а объем треугольной пирамиды, построенной на этих же векторах, равен 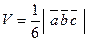 .
.
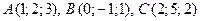 и
и 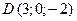 . Найти объем пирамиды.
. Найти объем пирамиды. Решение. Находим векторы
Решение. Находим векторы 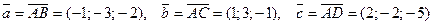 .
.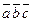 :
: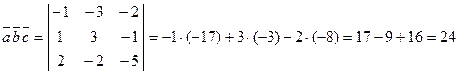 .
. Следовательно,
Следовательно, 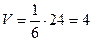 .
.