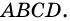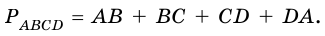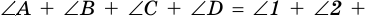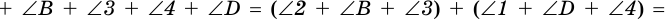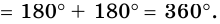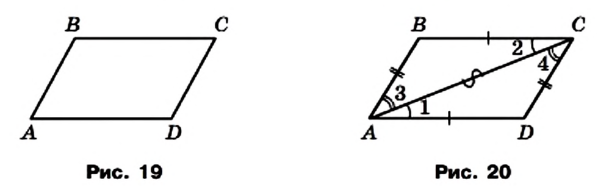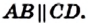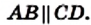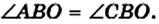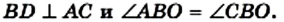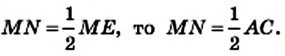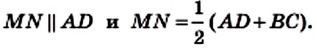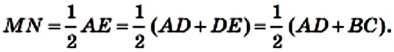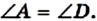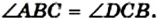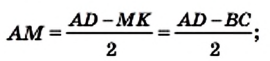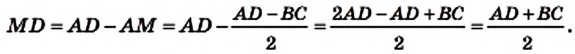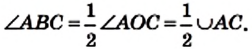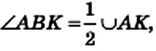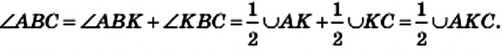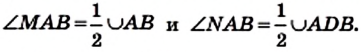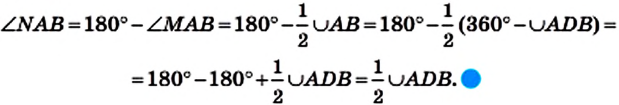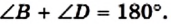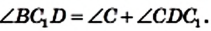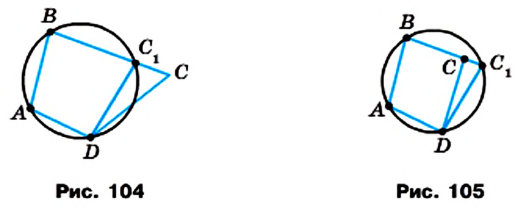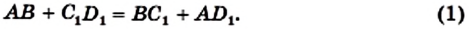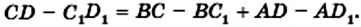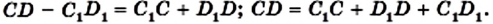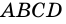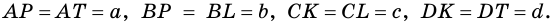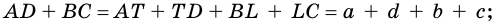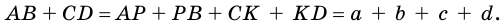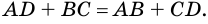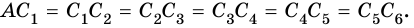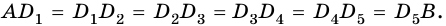Четырехугольника это отрезок соединяющий две его несоседние вершины

Математику уж затем учить надо, что она ум в порядок приводит

1) Два отрезка называют соседними , если они имеют общую точку ,являющуюся концом каждого из них.

2) Фигуру , ограниченную частью плоскости , являющуюся такими , что никакие два соседних отрезка не лежат на одной прямой и никакие два не соседних отрезка не имеют общих точек , вместе с этими отрезками, называют четырёхугольником .

3) Стороны четырёхугольника , являющиеся соседними отрезками , называют соседними сторонами четырёхугольника .

4) Вершины четырёхугольника , являющиеся концами одной стороны называют соседними вершинами четырехугольника .

5) Стороны четырёхугольника, не являющиеся соседними, называют противолежащими (противоположными) сторонами четырёхугольника .

6) Несоседние вершины четырёхугольника называют противолежащими (противоположными) вершинами четырёхугольника .

7) Сумму длин сторон четырёх угольника называют периметром четырехугольника .

8) Отрезок , соединяющий противолежащие вершины четырехугольника, называют диагональю четырехугольника .

9) Четырёхугольник , все углы которого меньше развёрнутого угла называют выпуклым четырёхугольником .

10) Сумма углов четырёхугольника равна 360°.

11) В четырёхугольнике только один из углов может быть больше развернутого.

1) Два отрезка называют соседними , если они имеют ______________________ ,являющуюся ___________________________ каждого из них.

2) Фигуру , ограниченную частью плоскости , являющуюся такими , что никакие два ________________ отрезка не лежат __________________________ и никакие ___________________ отрезка не имеют _____________________ , вместе с этими отрезками, называют четырёхугольником .

3) Стороны четырёхугольника , являющиеся соседними отрезками , называют _____________________ сторонами четырёхугольника .

4) Вершины четырёхугольника , являющиеся ________________________________ называют соседними вершинами четырехугольника .

5) Стороны четырёхугольника, не являющиеся соседними, называют ____________________________ сторонами четырёхугольника .

6) Несоседние вершины четырёхугольника называют _______________________________ вершинами четырёхугольника .

7) Сумму _______________________ четырёх угольника называют периметром четырехугольника .

8) Отрезок , соединяющий противолежащие вершины четырехугольника называют____________________ четырехугольника .

9) Четырёхугольник , все углы которого меньше развёрнутого угла называют ___________________ четырёхугольником .

10) Сумма углов четырёхугольника равна _______

11) В четырёхугольнике _____________________________ может быть больше развернутого.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Четырехугольник

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Определение четырехугольника

Определение 1. Четырехугольник − это замкнутая ломаная линия, состоящая из четырех звеньев.

Определение 2. Четырехугольник − геометрическая фигура (многоугольник), состоящая из четырех точек, никакие три из которых не лежат на одной прямой и последовательно соединенные четырьмя отрезками, называемыми сторонами четырехугольника.

Объединение четырехугольника и ограниченной им части плоскости также называют четырехугольником.

Любой четырехугольник разделяет плоскость на две части, одна из которых называется внутренней областью четырехугольника, а другая внешней областью четырехугольника.

Видео:Геометрия 8 класс (Урок№1 - Многоугольники. Четырёхугольник.)Скачать

Виды четырехугольников

Четырехугольники бывают следующих видов:

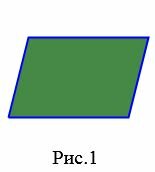
• Параллелограмм − четырехугольник, у которого противоположные стороны попарно вправны и параллельны (Рис.1).
• Трапеция − четырехугольник, у которого две противоположные стороны параллельны (Рис.2).
• Прямоугольник − четырехугольник, у которого все углы прямые (Рис.3).
• Ромб − четырехугольник, у которого все стороны равны (Рис.4).
• Квадрат − четырехугольник, у которого все стороны равны и все углы прямые (Рис.5).
• Дельтоид − четырехугольник, у которого есть две пары равных смежных сторон (Рис.6, Рис.6.1).
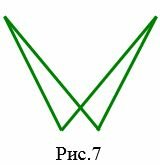
• Антипараллелограмм (или контрпараллелограмм)− четырехугольник, у которого противоположные стороны равны но не параллельны (с самопересечением) (Рис.7).

Видео:Четырёхугольник и его элементы Геометрия 8клСкачать

Обозначение четырехугольника

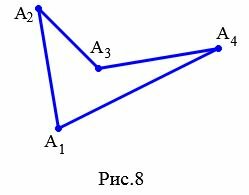
Обозначают четырехугольник буквами, стоящих при его вершинах. Называют четырехугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, четырехугольник на рисунке 8 называют ( small A_1A_2A_3A_4 ) или ( small A_4A_3A_2A_1 ) (Рис.8).

Видео:Четырёхугольник и его элементы – 8 класс геометрияСкачать

Соседние вершины четырехугольника

Вершины четырехугольника называются соседними, если они являются концами одной из его сторон.

На рисунке 8 вершины ( small A_2 ) и ( small A_3 ) являются соседними, так как они являются концами стороны ( small A_2A_3. )

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Смежные стороны четырехугольника

Стороны четырехугольника называются смежными, если они имеют общую вершину.

На рисунке 8 стороны ( small A_2A_3 ) и ( small A_3A_4 ) являются смежными, так как они имеют общую вершину ( small A_3. )

Видео:Математика 5 класс (Урок№29 - Четырёхугольники.)Скачать

Простой четырехугольник. Самопересекающийся четырехугольник

Четырехугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

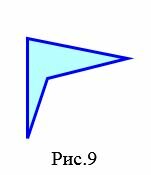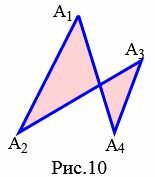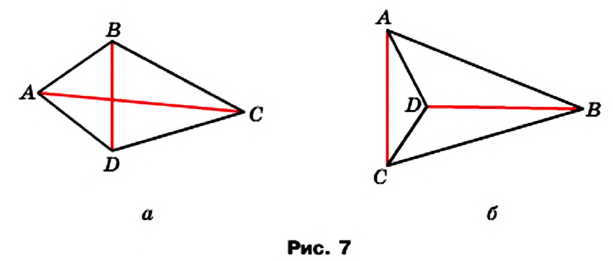
На рисунках 9 и 9.1 изображены простые четырехугольники так как стороны четырехугольников не имеют самопересечений. А на рисунке 10 четырехугольник не является простым, так как стороны ( small A_1A_4 ) и ( small A_2A_3 ) пересекаются. Такой четырехугольник называется самопересекающийся.

Видео:ЧЕТЫРЕХУГОЛЬНИК и его элементы. §1 геометрия 8 классСкачать

Выпуклый четырехугольник

Четырехугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

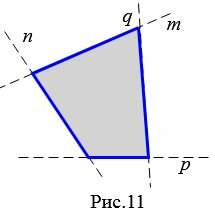На рисунке 11 четырехугольник лежит по одну сторону от прямых ( small m, n, p, q, ) проходящих через стороны четырехугольника. Поэтому такой четырехугольник выпуклый.

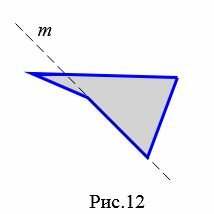На рисунке 12 прямая ( small m) делит четырехугольник на две части, т.е. четырехугольник не лежит по одну сторону от прямой ( small m). Следовательно, этот четырехугольник не является выпуклым.

Видео:Многоугольники. ЧетырёхугольникСкачать

Правильный четырехугольник

Простой четырехугольник называется правильным, если все его стороны равны и все углы равны. Квадрат является правильным четырехугольником, так как все его стороны равны и все его углы равны 90°. Среди четырехугольников других правильных четырехугольников не существует.

На рисунке 5 изображен правильный четырехугольник (квадрат), так как у данного четырехугольника все стороны равны и все углы равны. Четырехугольник (ромб) на на рисунке 4 не является правильным, так как все стороны четырехугольника равны, но все его углы не равны друг другу. Прямоугольник также не является правильным четырехугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Видео:Многоугольники. 8 класс.Скачать

Периметр четырехугольника

Сумма всех сторон четырехугольника называется периметром четырехугольника. Для четырехугольника ( small A_1A_2A_3A_4 ) периметр вычисляется из формулы:

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Угол четырехугольника

Углом (внутренним углом) четырехугольника при данной вершине называется угол между двумя сторонами четырехугольника, сходящимися к этой вершине. Если четырехугольник выпуклый, то все углы четырехугольника меньше 180°. Если же четырехугольник невыпуклый, то он имеет внутренний угол больше 180° (угол ( small alpha ) на рисунке 13).

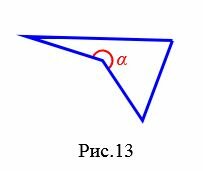Видео:8 класс. Геометрия. Четырехугольник: вершины, стороны, диагонали. Свойства параллелограмма. Урок #1Скачать

Внешний угол четырехугольника

Внешним углом четырехугольника при данной вершине называется угол смежный внутреннему углу четырехугольника при данной вершине.

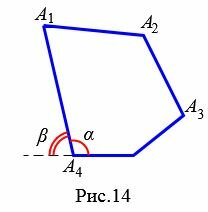На рисунке 14 угол α является внутренним углом четырехугольника при вершине ( small A_4, ) а углы β и γ являются внешними углами четырехугольника при этой же вершине. Очевидно, что при каждой вершине есть два внешних угла.

Видео:Геометрия. ЧетырехугольникиСкачать

Диагональ четырехугольника

Диагоналями называют отрезки, соединяющие две несоседние вершины четырехугольника.

Очевидно, что у четырехугольника две диагонали.

Видео:8 класс, 4 урок, ПараллелограммСкачать

Сумма углов четырехугольника

Для любого простого четырехугольника по крайней мере один диагональ делит его на два треугольника. Сумма углов треугольника равна 180°. Поэтому сумма углов простого четырехугольника равна 360°.

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Сумма внешних углов четырехугольника

Пусть задан четырехугольник ( small A_1A_2A_3A_4 .) Внешний угол при вершине ( small A_1) равен ( small 180°-angle A_1.) Аналогично, внешние углы при вершинах ( small A_2, A_3, A_4 ) равны ( small 180°-angle A_2, ) ( small 180°-angle A_3, ) ( small 180°-angle A_4, ) соответственно. Тогда сумма внешних углов четырехугольника равна:

Задача 1. Доказать, что длина любой стороны четырехугольника меньше суммы длин трех его сторон.

Решение. Рассмотрим произвольный четырехугольник ABCD (Рис.15). Покажем, например, что AB

Видео:ЧЕТЫРЁХУГОЛЬНИКСкачать

Четырехугольник и его элементы — определение и вычисление с доказательствами и примерами решения

Содержание:

Четырехугольником называют фигуру, состоящую из четырех точек и четырех последовательно соединяющих их отрезков.

Никакие три из этих точек не должны лежать на одной прямой, а соединяющие их отрезки не должны иметь никаких других общих точек, кроме данных.

Любой четырехугольник ограничивает некоторую часть плоскости, являющуюся внутренней областью четырехугольника.

На рисунке 1 изображен четырехугольник

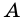
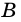
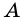
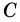
Вершины четырехугольника, являющиеся концами его стороны, называют соседними, несоседние вершины называют противолежащими. На рисунке 1 вершины и — соседние, и — противолежащие.

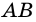
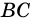
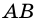
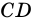
Стороны четырехугольника, имеющие общую вершину, называют соседними, а не имеющие общей вершины — противолежащими. На рис. 1 стороны и — соседние, и — противолежащие.

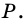
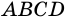
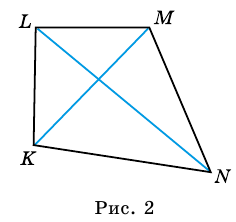
Сумму длин всех сторон четырехугольника называют его периметром. Периметр обозначают буквой Например, периметр четырехугольника можно обозначить как

Отрезки, соединяющие противолежащие вершины четырехугольника, называют диагоналями четырехугольника.

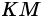
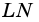
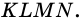
На рисунке 2 отрезки и — диагонали четырехугольника Каждый четырехугольник имеет две диагонали.

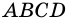
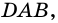
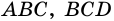
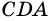
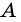
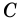
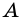
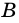
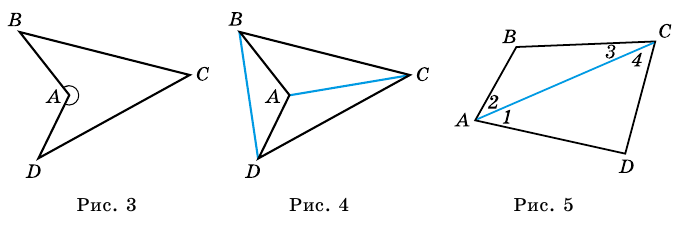
Углами четырехугольника называют углы и (рис. 1). Углы четырехугольника называют противолежащими, если их вершины — противолежащие вершины четырехугольника, и соседними, если их вершины — соседние вершины четырехугольника. На рисунке 1 углы и — противолежащие, и — соседние.

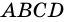
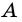
Один из углов четырехугольника может быть больше развернутого угла. Например, на рисунке 3 в четырехугольнике угол больше развернутого. Такой четырехугольник называют невыпуклым. Если все углы четырехугольника меньше 180°, его называют выпуклым. Диагонали выпуклого четырехугольника пересекаются (рис. 2), а невыпуклого не пересекаются (рис. 4).

Теорема (о сумме углов четырехугольника). Сумма углов четырехугольника равна 360°.

Доказательство:

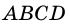
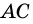
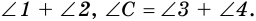
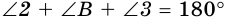
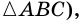
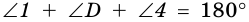
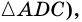
Пусть — некоторый четырехугольник. Проведем в нем диагональ (рис. 5). Тогда Учитывая, что (как сумма углов (как сумма углов будем иметь:

Пример:

Найдите углы четырехугольника, если их градусные меры относятся как 3 : 10 : 4 : 1. Выпуклым или невыпуклым является этот четырехугольник?

Решение:

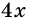
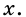
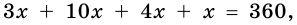
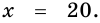
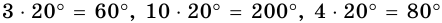
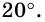
Пусть углы четырехугольника равны и Имеем уравнение откуда Следовательно, углы четырехугольника равны и Так как один из углов четырехугольника больше 180°, то этот четырехугольник — невыпуклый.

Ответ. 60°, 200°, 80°, 20°; невыпуклый.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Четырехугольник и его элементы

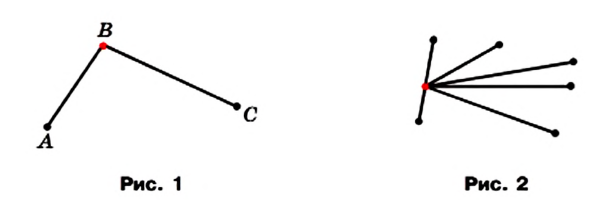
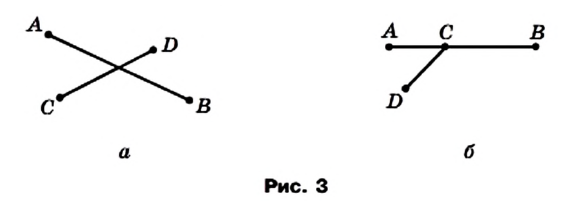
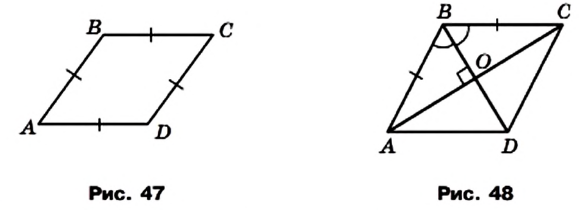
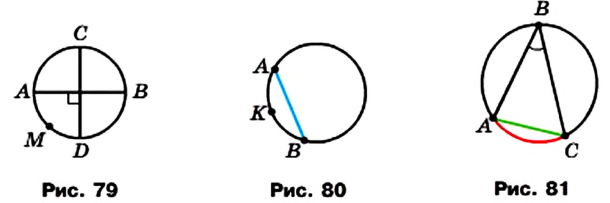
На рисунке 1 отрезки АВ и ВС имеют только одну общую точку В, которая является концом каждого из них. Такие отрезки называют соседними. На рисунке 2 каждые два отрезка являются соседними.

Отрезки АВ и CD на рисунке 3 не являются соседними.

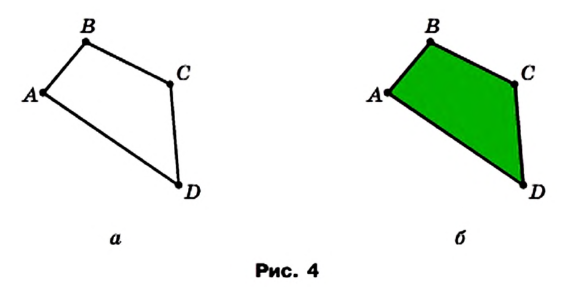
Рассмотрим фигуру, состоящую из четырех точек А, В, С, D и четырех отрезков АВ, ВС, CD, DA таких, что никакие два соседних отрезка не лежат на одной прямой и никакие два несоседних отрезка не имеют общих точек (рис. 4, а).

Фигура, образованная этими отрезками, ограничивает часть плоскости, выделенную на рисунке 4, б зеленым цветом. Эту часть плоскости вместе с отрезками АВ, ВС, CD и DA называют четырехугольником. Точки А, В, С, D называют вершинами четырехугольника, а отрезки АВ, ВС, CD, DA — сторонами четырехугольника.

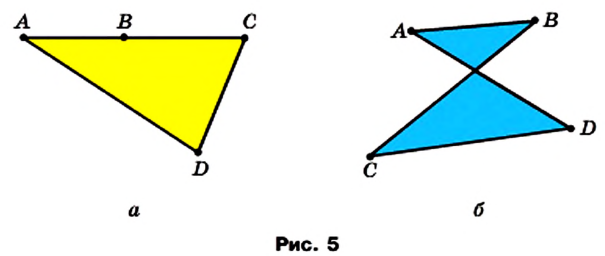
На рисунке 5 изображены фигуры, состоящие из четырех отрезков АВ, ВС, CD, DA и части плоскости, которую они ограничивают. Однако эти фигуры не являются четырехугольниками. Поясните почему.

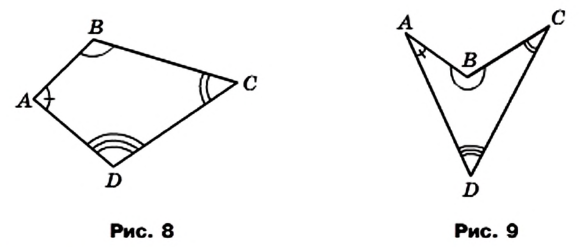
Стороны четырехугольника, являющиеся соседними отрезками, называют соседними сторонами четырехугольника. Вершины, являющиеся концами одной стороны, называют соседними вершинами многоугольника. Стороны, не являющиеся соседними, называют противолежащими сторонами четырехугольника. Несоседние вершины называют противолежащими вершинами четырехугольника.

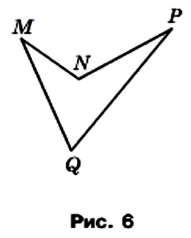
На рисунке 6 изображен четырехугольник, в котором, например, стороны MQ и MN являются соседними, а стороны NP и MQ — противолежащими. Вершины Q и Р — соседние, а вершины М и Р — противолежащие.

Четырехугольник называют и обозначают по его вершинам. Например, на рисунке 4, б изображен четырехугольник ABCD, а на рисунке 6 — четырехугольник MNPQ. В обозначении четырехугольника буквы, стоящие рядом, соответствуют соседним вершинам четырехугольника. Например, четырехугольник, изображенный на рисунке 6, можно обозначить еще и так: PQMN, или MQPN, или NPQM и т. д.

Сумму длин всех сторон четырехугольника называют периметром четырехугольника.

Отрезок, соединяющий противолежащие вершины четырехугольника, называют диагональю. На рисунке 7 отрезки АС и BD — диагонали четырехугольника АВСD.

Углы ABC, BCD, CDA, DAB (рис. 8) называют углами четырехугольника ABCD. В этом четырехугольнике каждый из них меньше развернутого угла. Такой четырехугольник называют выпуклым. Однако существуют четырехугольники, в которых не все углы меньше развернутого. Например, на рисунке 9 угол В четырехугольника ABCD больше 180°. Такой четырехугольник называют невыпуклым 1 .

Углы АВС и ADC называют противолежащими углами четырехугольника ABCD (рис. 8, 9). Также противолежащими являются углы BAD и BCD.

Теорема 1.1. Сумма углов четырехугольника равна 360°.

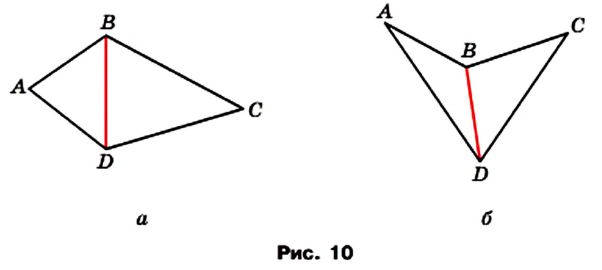
Доказательство. Проведем в четырехугольнике диагональ, разбивающую его на два треугольника. Например, на рисунке 10

1 Более подробно с понятием «выпуклость» вы ознакомитесь в п. 19.

это диагональ BD. Тогда сумма углов четырехугольника ABCD равна сумме углов треугольников ABD и CBD. Поскольку сумма углов треугольника равна 180°, то сумма углов четырехугольника равна 360°.

Следствие. В четырехугольнике только один из углов может быть больше развернутого.

Докажите это свойство самостоятельно.

Пример:

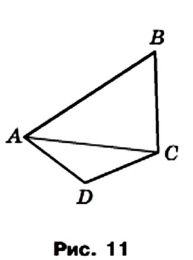
Докажите, что длина любой стороны четырехугольника меньше суммы длин трех остальных его сторон.

Решение:

Рассмотрим произвольный четырехугольник ABCD (рис. 11). Покажем, например, что АВ 1 В учебнике задачи на построение не обязательны для рассмотрения.

В треугольнике АВС известны две стороны АВ и ВС и угол В между ними. Следовательно, этот треугольник можно построить. Теперь можем от лучей АВ и СВ отложить углы, равные углам четырехугольника при вершинах А и С.

Проведенный анализ показывает, как строить искомый четырехугольник.

Строим треугольник по двум данным сторонам четырехугольника и углу между ними. На рисунке 12 это треугольник АВС. Далее от лучей АВ и СВ откладываем два известных угла четырехугольника. Два построенных луча пересекаются в точке D. Четырехугольник ABCD — искомый.

Параллелограмм. Свойства параллелограмма

Определение. Параллелограммом называют четырехугольник, у которого каждые две противолежащие стороны параллельны.

На рисунке 19 изображен параллелограмм ABCD. По определению параллелограмма имеем:

Рассмотрим некоторые свойства параллелограмма.

Теорема 2.1. Противолежащие стороны параллелограмма равны.

Доказательство. На рисунке 19 изображен параллелограмм ABCD. Докажем, что АВ = CD и ВС = AD.

Проведем диагональ АС. Докажем, что треугольники АВС и CDA равны (рис. 20).

В этих треугольниках сторона АС — общая, углы 1 и 2 равны как накрест лежащие при параллельных прямых ВС и AD и секущей АС, углы 3 и 4 равны как накрест лежащие при параллельных прямых АВ и CD и секущей АС. Следовательно, треугольники АВС и CDA равны по второму признаку равенства треугольников. Отсюда АВ = CD и ВС = AD.

Теорема 2.2. Противолежащие углы параллелограмма равны.

Доказательство. На рисунке 19 изображен параллелограмм ABCD. Докажем, что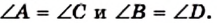
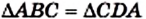
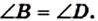
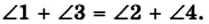
При доказательстве предыдущей теоремы было установлено, что (рис. 20). Отсюда Из равенства углов 1 и 2 и равенства углов 3 и 4 следует, что Следовательно,

Теорема 2.3. Диагонали параллелограмма точкой пересечения делятся пополам.

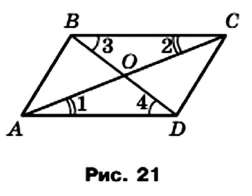
Доказательство. На рисунке 21 изображен параллелограмм ABCD, диагонали которого пересекаются в точке О. Докажем, что АО = ОС и ВО = OD.

Рассмотрим треугольники AOD и СОВ.
Имеем: 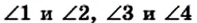равны как накрест лежащие при параллельных прямых AD и ВС и секущих АС и BD соответственно. Из теоремы 2.1 получаем: AD = ВС.

Следовательно, треугольники AOD и СОВ равны по второму признаку равенства треугольников. Отсюда АО = ОС, ВО = OD.

Определение. Высотой параллелограмма называют перпендикуляр, опущенный из любой точки прямой, содержащей сторону параллелограмма, на прямую, содержащую противолежащую сторону.

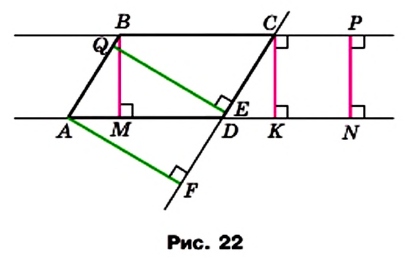
На рисунке 22 каждый из отрезков AF, QE, ВМ, PN, СК является высотой параллелограмма ABCD.

Из курса геометрии 7 класса вы знаете, что все точки одной из двух параллельных прямых равноудалены от другой прямой. Поэтому AF = QE и ВМ = PN = СК.

Говорят, что высоты ВМ, СК, PN проведены к сторонам ВС и AD, а высоты AF, QE — к сторонам АВ и CD.

Пример №1

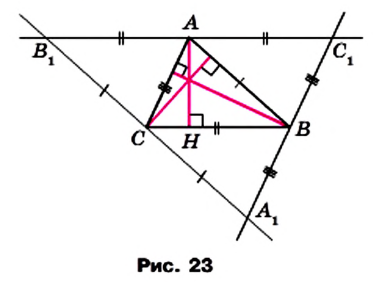
Докажите, что прямые, содержащие высоты треугольника, переcекаются в одной точке.

Решение:

Через каждую вершину данного треугольника АВС проведем прямую, параллельную противолежащей стороне. Получим треугольник 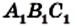(рис. 23).

Из построения следует, что четырехугольники — параллелограммы. Отсюда Следовательно, точка А является серединой отрезка

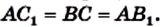
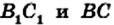
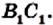
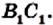
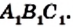
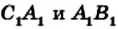
Поскольку прямые параллельны, то высота АН треугольника АВС перпендикулярна отрезку Таким образом, прямая АН — серединный перпендикуляр стороны треугольника Аналогично можно доказать, что прямые, содержащие две другие высоты треугольника АВС, являются серединными перпендикулярами сторон треугольника

Так как серединные перпендикуляры сторон треугольника пересекаются в одной точке, то утверждение теоремы доказано.

Пример №2

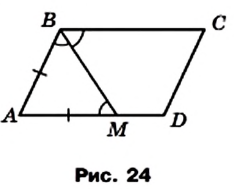
Биссектриса тупого угла параллелограмма делит его сторону в отношении 2 : 1, считая от вершины острого угла. Найдите стороны параллелограмма, если его периметр равен 60 см.

Решение:

Пусть биссектриса тупого угла В параллелограмма ABCD (рис. 24) пересекает сторону AD в точке М. По условию AM : MD = 2 : 1.

Углы ABM и CBM равны по условию.
Углы СВМ и AM В равны как накрест лежащие при параллельных прямых ВС и AD и секущей ВМ.

Тогда 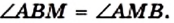Следовательно, треугольник ВАМ равнобедренный, отсюда АВ = AM.

Пусть MD = х см, тогда АВ =АМ = 2х см, AD = Зх см. Поскольку противолежащие стороны параллелограмма равны, то его периметр равен 2 (АВ + AD). Учитывая, что по условию периметр параллелограмма равен 60 см, получаем:

2 (2х + Зх) = 60;
х = 6.

Следовательно, АВ = 12 см, AD = 18 см.

Ответ: 12 см, 18 см.

Признаки параллелограмма

Определение параллелограмма позволяет среди четырехугольников распознавать параллелограммы. Этой же цели служат следующие три теоремы, которые называют признаками параллелограмма.

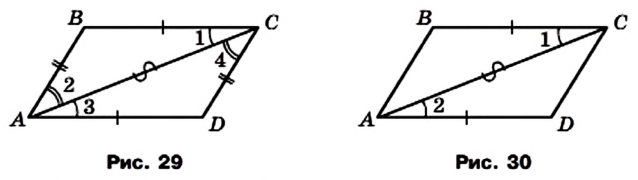
Теорема 3.1 (обратная теореме 2.1). Если в четырехугольнике каждые две противолежащие стороны равны, то этот четырехугольник — параллелограмм.

Доказательство. На рисунке 29 изображен четырехугольник ABCD, в котором АВ = CD и ВС = AD. Докажем, что четырехугольник ABCD — параллелограмм.

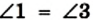
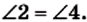
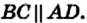
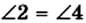
Проведем диагональ АС. Треугольники АВС и CDA равны по третьему признаку равенства треугольников. Отсюда и Углы 1 и 3 являются накрест лежащими при прямых ВС и AD и секущей АС. Следовательно, Аналогично из равенства следует, что

Таким образом, в четырехугольнике ABCD каждые две противолежащие стороны параллельны, поэтому этот четырехугольник — параллелограмм.

Теорема 3.2. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Доказательство. На рисунке 30 изображен четырехугольник ABCD, в котором ВС = AD и 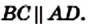Докажем, что четырехугольник ABCD — параллелограмм.

Проведем диагональ АС. В треугольниках АВС и CDA имеем: ВС = AD по условию, углы 1 и 2 равны как накрест лежащие при параллельных прямых ВС и AD и секущей АС, а сторона АС общая. Следовательно, треугольники АВС и CDA равны по первому признаку равенства треугольников. Отсюда АВ = CD. Значит, в четырехугольнике ABCD каждые две противолежащие стороны равны. Поэтому по теореме 3.1 четырехугольник ABCD — параллелограмм.

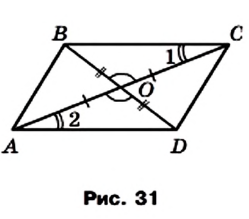
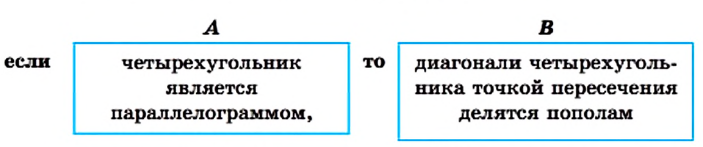
Теорема 3.3 (обратная теореме 2.3). Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Доказательство. На рисунке 31 изображен четырехугольник ABCD, в котором диагонали АС и BD пересекаются в точке О, причем АО = ОС и ВО = OD. Докажем, что четырехугольник ABCD — параллелограмм.

Поскольку углы ВОС и DOA равны как вертикальные, АО = ОС и ВО = OD, то треугольники ВОС и DOA равны по первому признаку равенства треугольников. Отсюда ВС = AD и 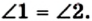Углы 1 и 2 являются накрест лежащими при прямых ВС и AD и секущей АС. Следовательно,

Таким образом, в четырехугольнике ABCD две противолежащие стороны равны и параллельны. По теореме 3.2 четырехугольник ABCD — параллелограмм.

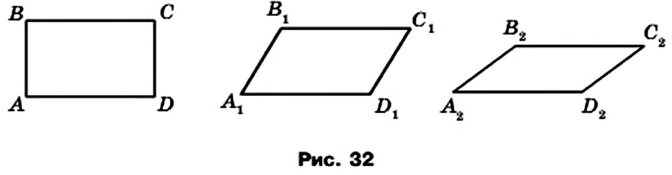
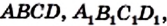
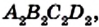
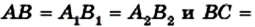
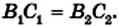
Вы знаете, что треугольник можно однозначно задать его сторонами, то есть задача построения треугольника по трем сторонам имеет единственное решение. Иначе обстоит дело с параллелограммом. На рисунке 32 изображены параллелограммы стороны которых равны, то есть Однако очевидно, что сами параллелограммы не равны.

Сказанное означает, что если четыре рейки скрепить так, чтобы образовался параллелограмм, то полученная конструкция не будет жесткой.

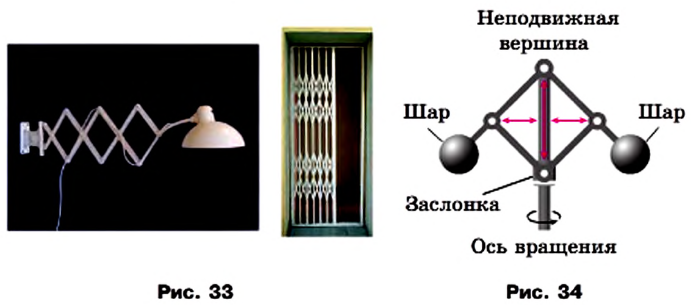
Это свойство параллелограмма широко используют на практике. Благодаря его подвижности лампу можно устанавливать в удобное для работы положение, а раздвижную решетку — отодвигать на нужное расстояние в дверном проеме (рис. 33).

На рисунке 34 изображена схема механизма, являющегося частью паровой машины. При увеличении скорости вращения оси шары отдаляются от нее под действием центробежной силы, тем самым поднимая заслонку, регулирующую количество пара. Механизм назван параллелограммом Уатта в честь изобретателя первой универсальной паровой машины.

Пример №3

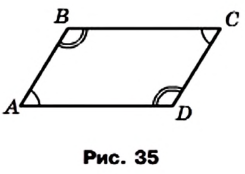
Докажите, что если в четырехугольнике каждые два противолежащих угла равны, то этот четырехугольник — параллелограмм.

Решение:

На рисунке 35 изображен четырехугольник ABCD, в котором 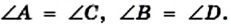Докажем, что четырехугольник ABCD — параллелограмм.

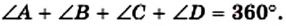
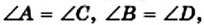
По теореме о сумме углов четырехугольника (теорема 1.1) Учитывая, что получим:

Поскольку углы А и В — односторонние углы при прямых AD и ВС и секущей АВ, а их сумма равна 180°, то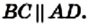
Аналогично доказываем, что

Следовательно, четырехугольник ABCD — параллелограмм.

Необходимо и достаточно

Из курса геометрии 7 класса вы узнали, что большинство теорем состоят из двух частей: условия (то, что дано) и заключения (то, что требуется доказать).

Если утверждение, выражающее условие, обозначить буквой А, а утверждение, выражающее заключение, — буквой В, то формулировку теоремы можно изобразить следующей схемой: если А, то В.
Например, теорему 2.3 можно сформулировать так:

Тогда теорему 3.3, обратную теореме 2.3, можно сформулировать так:

Часто в повседневной жизни в своих высказываниях мы пользуемся словами «необходимо», «достаточно». Приведем несколько примеров.

• Для того чтобы уметь решать задачи, необходимо знать теоремы.
• Если вы на математической олимпиаде правильно решили все предложенные задачи, то этого достаточно для того, чтобы занять первое место.

Употребление слов «необходимо» и «достаточно» тесно связано с теоремами.

Условие А является достаточным для заключения В. Вместе с тем делимость числа нацело на 5 (утверждение В) необходима для делимости числа нацело на 10 (утверждение А).

Приведем еще один пример:

В этой теореме утверждение А является достаточным условием для утверждения В, то есть для того, чтобы два угла были равны, достаточно, чтобы они были вертикальными. В этой же теореме утверждение В является необходимым условием для утверждения А, то есть для того, чтобы два угла были вертикальными, необходимо, чтобы они были равны. Отметим, что утверждение В не является достаточным условием для утверждения А. Действительно, если два угла равны, то это совсем не означает, что они вертикальные.

Итак, в любой теореме вида если А, то В утверждение А является достаточным для утверждения В, а утверждение В — необходимым для утверждения А.

Если справедлива не только теорема если А, то В, но и обратная теорема если В, то А, то А является необходимым и достаточным условием для В, а В — необходимым и достаточным условием для А.

Например, теоремы 3.3 и 2.3 являются взаимно обратными. На языке «необходимо — достаточно» этот факт можно сформулировать так: для того чтобы четырехугольник был параллелограммом, необходимо и достаточно, чтобы его диагонали точкой пересечения делились пополам.

Подчеркнем, что если в теореме есть слова «необходимо и достаточно», то она объединяет две теоремы: прямую и обратную (прямой теоремой может быть любая из двух теорем, тогда другая будет обратной). Следовательно, доказательство такой теоремы должно состоять из двух частей: доказательств прямой и обратной теорем. Теорему, объединяющую прямую и обратную теоремы, называют критерием.

Иногда вместо «необходимо и достаточно» говорят «тогда и только тогда». Например, взаимно обратные теоремы 2.1 и 3.1 можно объединить в следующий критерий:

• четырехугольник является параллелограммом тогда и только тогда, когда каждые две его противолежащие стороны равны.

Сформулируйте самостоятельно теорему 2.2 и ключевую задачу п. 3 в виде теоремы-критерия.

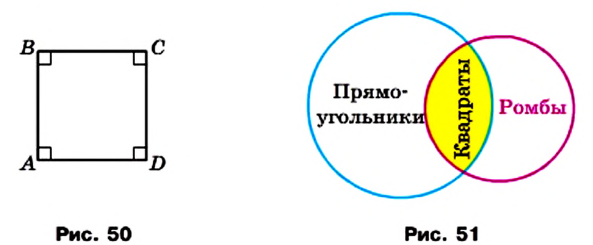
Прямоугольник

Параллелограмм — это четырехугольник, однако очевидно, что не каждый четырехугольник является параллелограммом. В этом случае говорят, что параллелограмм — это отдельный вид четырехугольника. Рисунок 42 иллюстрирует этот факт.

Существуют также отдельные виды параллелограммов.

Определение. Прямоугольником называют параллелограмм, у которого все углы прямые.

На рисунке 43 изображен прямоугольник ABCD.
Из определения следует, что прямоугольник имеет все свойства параллелограмма. В прямоугольнике:

• противолежащие стороны равны;
• диагонали точкой пересечения делятся пополам.

Однако прямоугольник имеет свои особые свойства, которыми не обладает параллелограмм, отличный от прямоугольника. Так, из определения следует, что все углы прямоугольника равны. Еще одно свойство прямоугольника выражает следующая теорема.

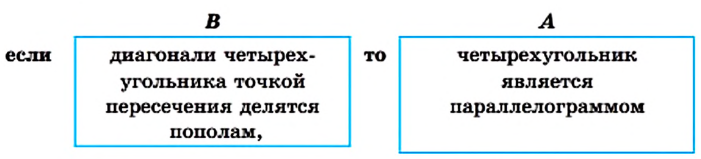
Теорема 4.1. Диагонали прямоугольника равны.

Доказательство. На рисунке 44 изображен прямоугольник ABCD. Докажем, что его диагонали АС и BD равны.
В прямоугольных треугольниках ABD и DCA катеты АВ и DC равны, а катет AD общий. Поэтому треугольники ABD и DCA равны по двум катетам. Отсюда BD = АС.

Определение прямоугольника позволяет среди параллелограммов распознавать прямоугольники. Этой же цели служат следующие две теоремы, которые называют признаками прямоугольника.

Теорема 4.2. Если один из углов параллелограмма прямой, то этот параллелограмм — прямоугольник.

Докажите эту теорему самостоятельно.

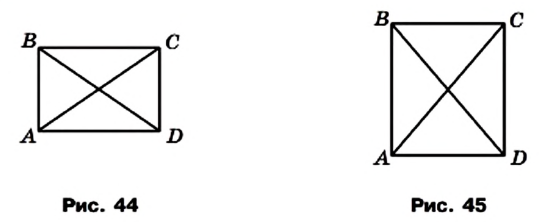
Теорема 4.3. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.

Доказательство. На рисунке 45 изображен параллелограмм ABCD, диагонали АС и BD которого равны. Докажем, что параллелограмм ABCD — прямоугольник.

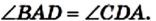
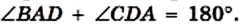
Рассмотрим треугольники ABD и DCА. У них АВ = CD, BD =АС, AD — общая сторона. Следовательно, эти треугольники равны по третьему признаку равенства треугольников. Отсюда Эти углы являются односторонними при параллельных прямых АВ и DC и секущей AD. Таким образом, Тогда Поэтому по теореме 4.2 параллелограмм ABCD — прямоугольник.

Ромб

Вы уже знаете, что прямоугольник — это отдельный вид параллелограмма. Познакомимся еще с одним видом параллелограмма — ромбом.

Определение. Ромбом называют параллелограмм, у которого все стороны равны.

На рисунке 47 изображен ромб ABCD.
Из определения следует, что ромб имеет все свойства параллелограмма. В ромбе:

• противолежащие углы равны;
• диагонали точкой пересечения делятся пополам.

Однако ромб имеет и свои особые свойства.

Теорема 5.1. Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Доказательство. На рисунке 48 изображен ромб ABCD, диагонали которого пересекаются в точке О. Докажем, что 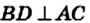и

Поскольку по определению ромба все его стороны равны, то треугольник АВС равнобедренный (АВ = ВС). По свойству диагоналей параллелограмма АО = ОС. Тогда отрезок ВО является медианой треугольника АВС, а значит, и высотой и биссектрисой этого треугольника. Следовательно,

Распознавать ромбы среди параллелограммов позволяют не только определение ромба, но и следующие две теоремы, которые называют признаками ромба.

Теорема 5.2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.

Теорема 5.3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм — ромб.

Докажите эти теоремы самостоятельно.

Квадрат

Определение. Квадратом называют прямоугольник, у которого все стороны равны.

На рисунке 50 изображен квадрат ABCD.

Из приведенного определения следует, что квадрат — это ромб, у которого все углы равны. Значит, квадрат является отдельным видом и прямоугольника, и ромба. Это иллюстрирует рисунок 51. Поэтому квадрат обладает всеми свойствами прямоугольника и ромба. Отсюда следует, что:

• все углы квадрата прямые;
• диагонали квадрата равны, перпендикулярны и являются биссектрисами его углов.

Средняя линия треугольника

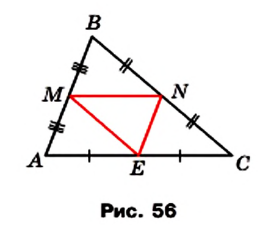
Определение. Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.

На рисунке 56 отрезки MN, NE, ЕМ — средние линии треугольника АВС.

Теорема 7.1. Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине.

Доказательство. Пусть MN — средняя линия треугольника АВС (рис. 57). Докажем, что

На прямой MN отметим точку Е так, что MN = NE (рис. 57). Соединим отрезком точки Е и С. Поскольку точка N является серединой отрезка ВС, то BN = NC. Углы 1 и 2 равны как вертикальные. Следовательно, треугольники MBN и ECN равны по первому признаку равенства треугольников. Отсюда 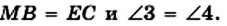Учитывая, что AM = ВМ, получим: ЕС = AM. Углы 3 и 4 являются накрест лежащими при прямых АВ и ЕС и секущей ВС. Тогда

Таким образом, в четырехугольнике АМЕС стороны AM и ЕС параллельны и равны. Следовательно, по теореме 3.2 четырехугольник АМЕС является параллелограммом. Отсюда 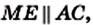то есть

Также ME = АС. Поскольку

Пример №4

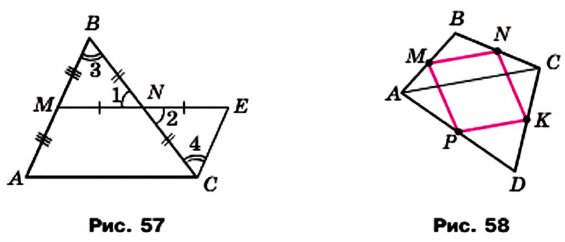
Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.

Решение:

В четырехугольнике ABCD точки М, N, К и Р — середины сторон АВ, ВС, CD и AD соответственно (рис. 58).
Отрезок MN — средняя линия треугольника АВС. По свойству средней линии треугольника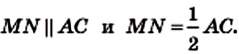
Отрезок РК — средняя линия треугольника ADC. По свойству средней линии треугольника

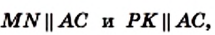
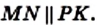
Поскольку то
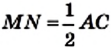
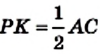
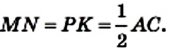
Из равенств и получаем:
Следовательно, в четырехугольнике MNKP стороны MN и РК равны и параллельны, поэтому четырехугольник MNKP — параллелограмм.

Трапеция

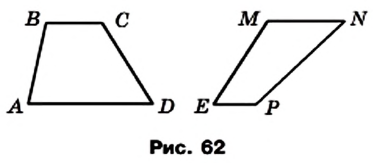
Определение. Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Каждый из четырехугольников, изображенных на рисунке 62, является трапецией.

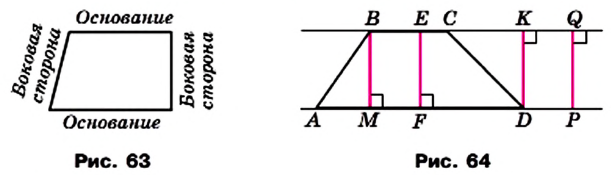
Параллельные стороны трапеции называют основаниями, а непараллельные — боковыми сторонами (рис. 63).

В трапеции ABCD 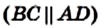углы Аи D называют углами при основании AD, а углы В и С — углами при основании ВС.

Определение. Высотой трапеции называют перпендикуляр, опущенный из любой точки прямой, содержащей одно из оснований, на прямую, содержащую другое основание.

На рисунке 64 каждый из отрезков ВМ, EF, DK, PQ является высотой трапеции ABCD. Длины этих отрезков равны расстоянию между параллельными прямыми ВС и AD. Поэтому ВМ = EF = DK = PQ.

На рисунке 65 изображена трапеция ABCD, у которой боковые стороны АВ и CD равны. Такую трапецию называют равнобокой или равнобедренной.

Если боковая сторона трапеции является ее высотой, то такую трапецию называют прямоугольной (рис. 66).

Трапеция — это отдельный вид четырехугольника. Связь между четырехугольниками и их отдельными видами показана на рисунке 67.

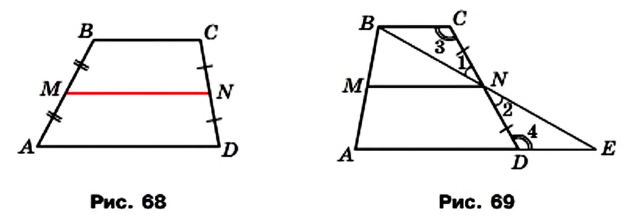
Определение. Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.

На рисунке 68 отрезок MN — средняя линия трапеции ABCD.

Теорема 8.1. Средняя линия трапеции параллельна основаниям и равна половине их суммы.

Доказательство. Пусть MN — средняя линия трапеции ABCD (рис. 69). Докажем, что

Проведем прямую BN и точку ее пересечения с прямой AD обозначим буквой Е.

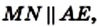
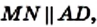
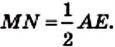
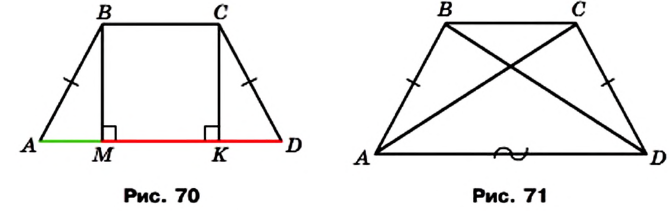
Поскольку точка N — середина отрезка CD, то CN = ND. Углы 1 и 2 равны как вертикальные, а углы 3 и 4 равны как накрест лежащие при параллельных прямых ВС и АЕ и секущей CD. Следовательно, треугольники BCN и EDN равны по второму признаку равенства треугольников. Отсюда ВС = DE и BN = NE. Тогда отрезок MN — средняя линия треугольника АВЕ. Из этого следует, что то есть и Имеем:

Пример №5 (свойства равнобокой трапеции)

Докажите, что в равнобокой трапеции:

1. углы при каждом основании равны;
2. диагонали равны;
3. высота трапеции, проведенная из вершины тупого угла, делит основание трапеции на два отрезка, меньший из которых равен половине разности оснований, а больший — половине суммы оснований (средней линии трапеции).

Решение:

Рассмотрим равнобокую трапецию ABCD (АВ = CD).
1) Проведем высоты ВМ и СК (рис. 70). Поскольку АВ = CD и ВМ = СК, то прямоугольные треугольники АМВ и DKC равны по катету и гипотенузе. Тогда

Имеем: 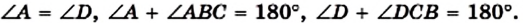Следовательно,

2) Рассмотрим треугольники ACD и DBA (рис. 71).

Имеем: АВ = CD, AD — общая сторона, углы BAD и CDA равны как углы при основании равнобокой трапеции. Следовательно, треугольники ACD и DBA равны по двум сторонам и углу между ними. Тогда АС = BD.
3) В четырехугольнике ВМКС (рис. 70) 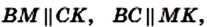угол ВМК прямой. Следовательно, этот четырехугольник является прямоугольником. Отсюда МК = ВС.
Из равенства треугольников АМВ и DKC следует, что 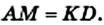Тогда

Центральные и вписанные углы

Определение. Центральным углом окружности называют угол с вершиной в центре окружности.

На рисунке 76 угол АОВ — центральный. Стороны этого угла пересекают окружность в точках А и В. Эти точки делят окружность на две дуги, выделенные на рисунке 76 разным цветом.

Точки А и В называют концами дуги, они принадлежат каждой из выделенных дуг. Каждую из этих дуг можно обозначить так: (читают: «дуга АВ»).

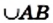
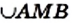
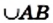
Однако по записи невозможно отличить дуги на рисунке 76. Если на какой-нибудь из двух дуг отметить точку (на рисунке 77 это точка М), то понятно, что обозначение относится к «синей» дуге. Если на одной из двух дуг АВ отмечена точка, то договоримся, что обозначение относится к дуге, которой эта точка не принадлежит (на рисунке 77 это «зеленая» дуга).

Дуга АВ принадлежит центральному углу АОВ (рис. 77). В этом случае говорят, что центральный угол АОВ опирается на дугу АВ.

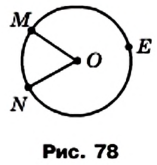
Каждая дуга окружности, как и вся окружность, имеет градусную меру. Градусную меру всей окружности считают равной 360°. Если центральный угол MON опирается на дугу MN (рис. 78), то градусную меру дуги MN считают равной градусной мере угла MON и записывают: 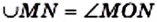(читают: «градусная мера дуги MN равна градусной мере угла MON). Градусную меру дуги MEN (рис. 78) считают равной 360° —

На рисунке 79 изображена окружность, в которой проведены два перпендикулярных диаметра АВ и CD.

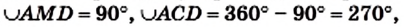
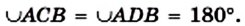
Тогда Каждую из дуг АСВ и ADB называют полуокружностью. На рисунке 79 полуокружностями являются также дуги CAD и CBD.

О хорде, соединяющей концы дуги, говорят, что хорда стягивает дугу. На рисунке 80 хорда АВ стягивает каждую из дуг АВ и АКВ.

Любая хорда стягивает две дуги, сумма градусных мер которых равна 360°.

Определение. Вписанным углом окружности называют угол, вершина которого принадлежит окружности, а стороны пересекают окружность.

На рисунке 81 угол АВС — вписанный. Дуга АС принадлежит этому углу, а дуга АВС — не принадлежит. В таком случае говорят, что вписанный угол АВС опирается на дугу АС. Также можно сказать, что вписанный угол АВС опирается на хорду АС.

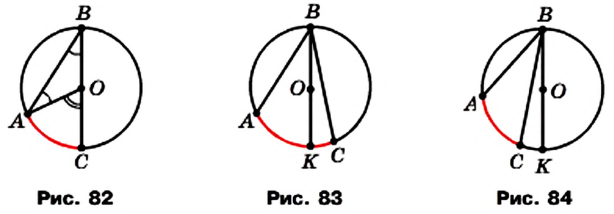
Теорема 9.1. Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

Доказательство. О На рисунке 81 угол АВС вписанный.

Докажем, что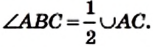
Рассмотрим три случая расположения центра О окружности относительно вписанного угла АВС.

Случай 1. Центр О принадлежит одной из сторон угла, например стороне ВС (рис. 82).
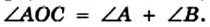
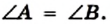
Проведем радиус ОА. Центральный угол АОС — внешний угол равнобедренного треугольника АВО (стороны ОА и ОВ равны как радиусы). Тогда Однако Отсюда

Случай 2. Центр О принадлежит углу, однако не принадлежит ни одной из его сторон (рис. 83).
Проведем диаметр ВК. Согласно доказанному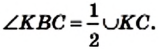
Имеем:

Случай 3. Центр О не принадлежит углу (рис. 84).
Для третьего случая проведите доказательство самостоятельно.

Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 85).

Следствие 2. Вписанный угол, опирающийся на диаметр (полуокружность), — прямой (рис. 86).

Докажите эти свойства самостоятельно.

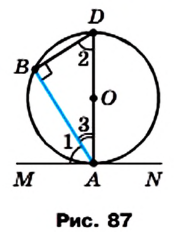
Пример №6 (свойство угла между касательной и хордой).

Отрезок АВ — хорда окружности с центром О (рис. 87). Через точку А проведена касательная MN. Докажите, что

Решение:

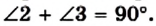
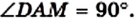
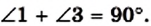
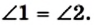
Проведем диаметр AD (рис. 87). Тогда угол В равен 90° как вписанный, опирающийся на диаметр AD. В прямоугольном треугольнике ABD Поскольку MN — касательная, то Тогда Получаем, что
Следовательно,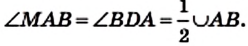
Имеем:

Пример №7

Постройте касательную к данной окружности, проходящую через данную точку, лежащую вне окружности.

Решение:

На рисунке 88 изображены окружность с центром О и точка М, лежащая вне этой окружности.

Пусть X — такая точка окружности, что прямая MX является касательной (рис. 88). Тогда угол МХО прямой. Следовательно, его можно рассматривать как вписанный в окружность с диаметром МО.

Проведенный анализ показывает, как провести построение.

Построим отрезок МО и разделим его пополам (рис. 89). Пусть точка К — его середина. Построим окружность радиуса КО с центром К. Обозначим точки пересечения построенной и данной окружностей буквами Е и F. Тогда каждая из прямых ME и MF является искомой касательной.

Действительно, угол МЕО равен 90° как вписанный угол, опирающийся на диаметр МО. Отрезок ОЕ — радиус данной окружности. Тогда по признаку касательной прямая ME — искомая касательная.

Описанная и вписанная окружности четырехугольника

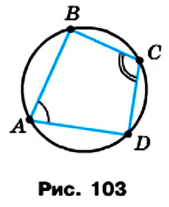
Определение. Окружность называют описанной около четырехугольника, если она проходит через все его вершины.

На рисунке 103 изображена окружность, описанная около четырехугольника ABCD. В этом случае также говорят, что четырехугольник вписан в окружность.

Теорема 10.1. Если четырехугольник является вписанным в окружность, то сумма его противолежащих углов равна 180°.

Доказательство. Пусть четырехугольник ABCD вписан в окружность (рис. 103). Докажем, что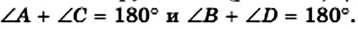
Поскольку углы А и С являются вписанными, то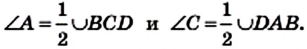
Имеем: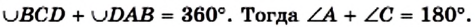
Аналогично можно показать, что

Вы знаете, что около любого треугольника можно описать окружность. Однако не всякий четырехугольник обладает таким свойством. Например, нельзя описать окружность около параллелограмма, отличного от прямоугольника. Распознавать четырехугольники, около которых можно описать окружность, позволяет следующая теорема.

Теорема 10.2 (обратная теореме 10.1). Если в четырехугольнике сумма противолежащих углов равна 180°, то около него можно описать окружность.

Доказательство. Рассмотрим четырехугольник ABCD, в котором 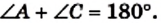Докажем, что около него можно описать окружность.

Предположим, что около этого четырехугольника нельзя описать окружность. Опишем окружность около треугольника ABD. По предположению точка С не принадлежит этой окружности. Поэтому возможны два случая.

Случай 1. Точка С лежит вне описанной окружности треугольника ABD (рис. 104).

Пусть сторона ВС пересекает окружность в точке Четырехугольник вписан в окружность. Тогда по теореме 10.1 получаем, что Но по условию Отсюда Однако это равенство выполняться не может, так как по свойству внешнего угла треугольника

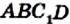
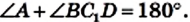
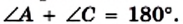
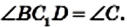
Итак, точка С не может лежать вне окружности, описанной около треугольника ABD.

Случай 2. Точка С лежит внутри описанной окружности треугольника ABD (рис. 105). Рассуждая аналогично, можно показать, что точка С не может лежать внутри рассматриваемой окружности. Убедитесь в этом самостоятельно.

Таким образом, предположив, что точка С не принадлежит окружности, описанной около треугольника ABD, мы получили противоречие.

Теорему 10.2 можно рассматривать как признак принадлежности четырех точек одной окружности.

Если четырехугольник вписан в окружность, то существует точка, равноудаленная от всех его вершин (центр описанной окружности). Чтобы найти эту точку, достаточно найти точку пересечения серединных перпендикуляров двух соседних сторон четырехугольника.

Определение. Окружность называют вписанной в четырехугольник, если она касается всех его сторон.

На рисунке 106 изображена окружность, вписанная в четырехугольник ABCD. В этом случае также говорят, что четырехугольник описан около окружности.

Теорема 10.3. Если четырехугольник является описанным около окружности, то суммы его противолежащих сторон равны.

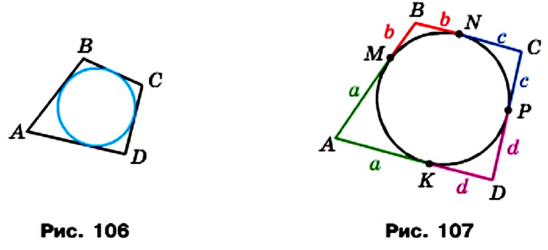
Доказательство. Пусть четырехугольник ABCD описан около окружности (рис. 107). Докажем, что АВ + CD = ВС + AD.

Точки М, N, Р, К — точки касания окружности со сторонами четырехугольника.

Поскольку отрезки касательных, проведенных к окружности через одну точку, равны, то АК =АМ, ВМ = BN, CN = СР, DP = DK. Пусть АК = а, ВМ = b, CN = с, DP = d.

Тогда АВ + CD = a + b + c + d,
ВС + AD = b + c + a + d.

Следовательно, АВ + CD = ВС + AD.

Вы знаете, что в любой треугольник можно вписать окружность. Однако не всякий четырехугольник обладает таким свойством. Например, нельзя вписать окружность в прямоугольник, отличный от квадрата. Распознавать четырехугольники, в которые можно вписать окружность, позволяет следующая теорема.

Теорема 10.4. Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность.

Доказательство. Рассмотрим выпуклый четырехугольник ABCD, в котором АВ + CD = ВС + AD. Докажем, что в него можно вписать окружность.

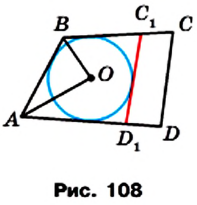
Пусть биссектрисы углов А и В пересекаются в точке О (рис. 108). Тогда точка О равноудалена от сторон АВ, ВС и AD. Следовательно, существует окружность с центром в точке О, которая касается этих трех сторон.

Предположим, что эта окружность не касается стороны CD. Тогда возможны два случая.

Случай 1. Сторона CD не имеет общих точек с построенной окружностью.
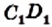
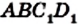
Проведем касательную параллельно стороне CD (рис. 108). Четырехугольник описан около окружности. Тогда по теореме 10.3 получаем, что

Однако по условию

Вычтем из равенства (2) равенство (1):

Отсюда имеем:

Это равенство противоречит утверждению, доказанному в ключевой задаче п. 1.

Итак, сторона CD должна иметь общие точки с рассматриваемой окружностью.

Случай 2. Сторона CD имеет две общие точки с построенной окружностью.

Рассуждая аналогично, можно показать, что сторона CD не может иметь две общие точки с построенной окружностью. Убедитесь в этом самостоятельно.

Таким образом, предположив, что построенная окружность не касается стороны CD, мы получили противоречие.

Если четырехугольник описан около окружности, то существует точка, равноудаленная от всех его сторон (центр вписанной окружности). Чтобы найти эту точку, достаточно найти точку пересечения биссектрис двух соседних углов этого четырехугольника.

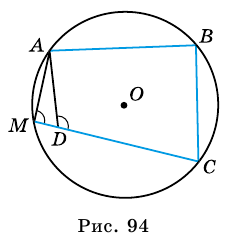
Пример №8 (признак принадлежности четырех точек одной окружности).

Точки А, М, N, В таковы, что 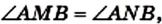причем точки M и N лежат в одной полуплоскости относительно прямой АВ. Докажите, что точки А, М, N, В лежат на одной окружности.

Решение:

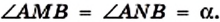
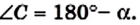
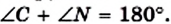
Пусть Около треугольника АМВ опишем окружность (рис. 109). Пусть С — произвольная точка окружности, не принадлежащая дуге АМВ. Тогда четырехугольник АСВМ вписан в окружность. Отсюда Имеем: Следовательно, по теореме 10.2 около четырехугольника ACBN можно описать окружность. Поскольку около треугольника АВС можно описать только одну окружность, то этой окружности принадлежат как точка М, так и точка N.

Сумма углов четырехугольника

• Сумма углов четырехугольника равна 360°.

Параллелограмм

• Параллелограммом называют четырехугольник, у которого каждые две противолежащие стороны параллельны.

Свойства параллелограмма

• Противолежащие стороны параллелограмма равны.
• Противолежащие углы параллелограмма равны.
• Диагонали параллелограмма точкой пересечения делятся пополам.

Высота параллелограмма

• Высотой параллелограмма называют перпендикуляр, опущенный из любой точки прямой, содержащей сторону параллелограмма, на прямую, содержащую противолежащую сторону.

Признаки параллелограмма

• Если в четырехугольнике каждые две противолежащие стороны равны, то этот четырехугольник — параллелограмм.
• Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
• Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Прямоугольник

• Прямоугольником называют параллелограмм, у которого все углы прямые.

Особое свойство прямоугольника

• Диагонали прямоугольника равны.

Признаки прямоугольника

• Если один из углов параллелограмма прямой, то этот параллелограмм — прямоугольник.
• Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.

Ромб

• Ромбом называют параллелограмм, у которого все стороны равны.

Особое свойство ромба

• Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Признаки ромба

• Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
• Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм — ромб.

Квадрат

• Квадратом называют прямоугольник, у которого все стороны равны.

Средняя линия треугольника

• Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

• Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине.

Трапеция

• Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Высота трапеции

• Высотой трапеции называют перпендикуляр, опущенный из любой точки прямой, содержащей одно из оснований, на прямую, содержащую другое основание.

Средняя линия трапеции

• Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.

Свойство средней линии трапеции

• Средняя линия трапеции параллельна основаниям и равна половине их суммы.

Центральный угол окружности

• Центральным углом окружности называют угол с вершиной в центре окружности.

Вписанный угол окружности

• Вписанным углом окружности называют угол, вершина которого принадлежит окружности, а стороны пересекают окружность.

Градусная мера вписанного угла окружности

• Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

Свойства вписанных углов

• Вписанные углы, опирающиеся на одну и ту же дугу, равны.
• Вписанный угол, опирающийся на диаметр (полуокружность), — прямой.

Окружность, описанная около четырехугольника

• Окружность называют описанной около четырехугольника, если она проходит через все его вершины.

Свойство четырехугольника, вписанного в окружность

• Если четырехугольник является вписанным в окружность, то сумма его противолежащих углов равна 180°.

Признак четырехугольника, около которого можно описать окружность

• Если в четырехугольнике сумма противолежащих углов равна 180°, то около него можно описать окружность.

Окружность, вписанная в четырехугольник

• Окружность называют вписанной в четырехугольник, если она касается всех его сторон.

Свойство окружности, описанной около четырехугольника

• Если четырехугольник является описанным около окружности, то суммы его противолежащих сторон равны.

Признак четырехугольника, в который можно вписать окружность

• Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность.

Вписанные и описанные четырехугольники

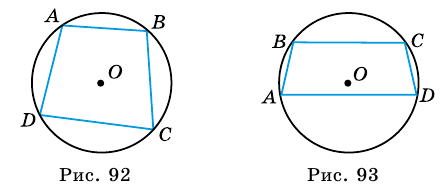
Четырехугольник называют вписанным в окружность, если все его вершины лежат на окружности. Окружность при этом называют описанной около четырехугольника (рис. 92).

Теорема 1 (свойство углов вписанного четырехугольника). Сумма противолежащих углов вписанного четырехугольника равна 180°.

Доказательство:

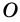
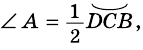
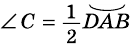
Пусть в окружность с центром вписан четырехугольник (рис. 92). Тогда (по теореме о вписанном угле).

Поэтому 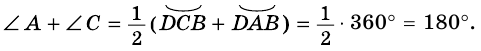Тогда

Следствие 1. Если около трапеции можно описать окружность, то трапеция равнобокая.

Доказательство:

Пусть трапеция вписана в окружность, (рис. 93). Тогда Но в трапеции Поэтому Следовательно, — равнобокая трапеция (по признаку равнобокой трапеции).

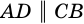
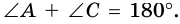
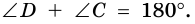
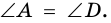
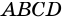
Как известно из курса геометрии 7 класса, около любого треугольника можно описать окружность. Для четырехугольников это не так.

Теорема 2 (признак вписанного четырехугольника). Если в четырехугольнике сумма двух противолежащих углов равна 180°, то около него можно описать окружность.

Доказательство:

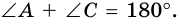
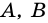
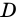
Пусть в четырехугольнике Проведем через точки и окружность. Докажем (методом от противного), что вершина четырехугольника также будет лежать на этой окружности.

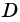
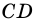
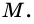
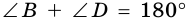
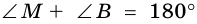
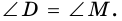
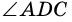
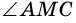
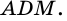
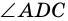
1) Допустим, что вершина лежит внутри круга (рис. 94). Продолжим до пересечения с окружностью в точке Тогда (по условию) и (по свойству углов вписанного четырехугольника). Тогда Но — внешний, a — не смежный с ним внутренний угол треугольника Поэтому должен быть больше, чем

Пришли к противоречию, значит, наше предположение ошибочно, и точка 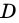не может лежать внутри круга.

2) Аналогично можно доказать, что вершина 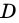не может лежать вне круга.

3) Следовательно, точка 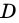лежит на окружности, ограничивающей круг (рис. 92), а значит около четырехугольника можно описать окружность.

Следствие 1. Около любого прямоугольника можно описать окружность.

Следствие 2. Около равнобокой трапеции можно описать окружность.

Заметим, что, как и в треугольнике, центром описанной около четырехугольника окружности является точка пересечения серединных перпендикуляров к его сторонам, поскольку она равноудалена от всех его вершин. Например, в прямоугольнике такой точкой является точка пересечения диагоналей.

Четырехугольник называют описанным около окружности, если все его стороны касаются окружности. Окружность при этом называют вписанной в четырехугольник (рис. 95).

Теорема 3 (свойство сторон описанного четырехугольника). В описанном четырехугольнике суммы противолежащих сторон равны.

Доказательство:

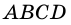
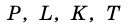
Пусть четырехугольник — описанный, — точки касания (рис. 96). По свойству отрезков касательных, проведенных из одной точки к окружности,

Ha рисунке 96 равные отрезки обозначены одинаковым цветом.

Тогда

Следовательно,

Как известно из курса геометрии 7 класса, в любой треугольник можно вписать окружность. Для четырехугольников это не так.

Теорема 4 (признак описанного четырехугольника). Если в четырехугольнике суммы противолежащих сторон равны, то в этот четырехугольник можно вписать окружность.

Доказательство этой теоремы является достаточно громоздким, поэтому его не приводим.

Следствие. В любой ромб можно вписать окружность.

Как и в треугольнике, центром окружности, вписанной в четырехугольник, является точка пересечения биссектрис его углов. Так как диагонали ромба являются биссектрисами его углов, то центр вписанной в ромб окружности — точка пересечения диагоналей.

Теорема Фалеса

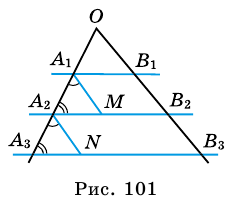
Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Доказательство:

Пусть параллельные прямые пересекают стороны угла с вершиной (рис. 101), при этом Докажем, что

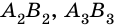
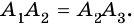
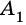
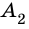
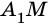
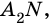
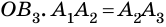
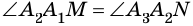
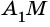
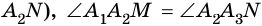
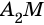
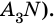
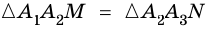
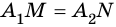
1) Проведем через точки и прямые и параллельные прямой (по условию), (как соответственные углы при параллельных прямых и (как соответственные углы при параллельных прямых и Поэтому

(по стороне и двум прилежащим к ней углам), а значит, (как соответственные стороны равных треугольников).

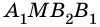
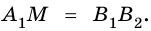
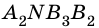
2) Четырехугольник — параллелограмм (по построению). Поэтому Аналогично -параллелограмм, поэтому

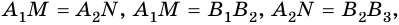
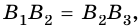
Таким образом, следовательно что и требовалось доказать.

Следствие. Параллельные прямые, пересекающие две данные прямые и отсекающие на одной из них равные отрезки, отсекают равные отрезки и на другой прямой.

С помощью линейки без делений по теореме Фалеса возможно разделить отрезок на любое количество равных частей.

Пример №9

Разделите отрезок 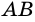на б равных частей.

Решение:

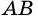
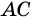
1) Пусть — данный отрезок (рис. 102). Проведем произвольный луч и отложим на нем циркулем последовательно 6 отрезков:

2) Через точки 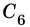и проведем прямую.

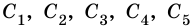
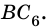
3) Через точки — с помощью угольника и линейки проведем прямые, параллельные прямой Тогда по теореме Фалеса эти прямые разделят отрезок АВ на 6 равных частей:

Фалес Милетский — древнегреческий математик и астроном. По давней традиции его считают одним из так называемых семи мудрецов света, ведь он был одним из самых выдающихся математиков своего времени.

В молодые годы любознательный юноша отправился путешествовать по Египту с целью познакомиться с египетской культурой и Фалес не только быстро изучил то, что в то время уже было известно египетским ученым, но и сделал ряд собственных научных открытий. Он самостоятельно определил высоту египетских пирамид по длине их тени, чем очень удивил египетского фараона Амазиса, а вернувшись на родину, создал в Милети философскую школу.

По мнению историков Фалес был первым, кто познакомил греков с геометрией и стал первым греческим астрономом. Он предсказал солнечное затмение, произошедшее 28 мая 585 года до н. э.

На гробнице Фалеса высечена надпись: «Насколько мала эта гробница, настолько велика слава этого царя астрономов в области звезд».

• Четырехугольники и окружность
• Параллелограмм, его свойства и признаки
• Площадь параллелограмма
• Прямоугольник и его свойства
• Сумма углов треугольника
• Внешний угол треугольника
• Свойство точек биссектрисы угла
• Свойство катета прямоугольного треугольника, лежащего против угла в 30°

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🎦 Видео

Четырехугольники. Вебинар | МатематикаСкачать

Отрезок, соединяющий середины диагоналей трапецииСкачать

Средняя линия треугольника и трапеции. 8 класс.Скачать