Четырехугольник является одновременно вписанным и описанным

Четырехугольник называется вписанным, если все его вершины лежат на окружности.

Вписанные и описанные четырехугольники

Четырехугольник называется описанным, если все его стороны касаются некоторой окружности.

Для того, чтобы четырехугольник был вписанным, необходимо и достаточно, чтобы сумма его противолежащих углов равнялась 180°.

Необходимость. Пусть четырехугольник ABCD вписан в окружность с центром в точке O.

По теореме 6.1 ∠ A B C + ∠ A D C = 1 2 ∪ A D C + 1 2 ∪ A B C = 1 2 ( ∪ A D C + ∪ A B C ) = 180 ˆ . Аналогично ∠ B A D + ∠ B C D = 180 ˆ .

Достаточность. Пусть ABCD – данный четырехугольник и ∠ B A D + ∠ B C D = 180 ˆ . Существует окружность, проходящая одновременно через три точки A, B и D (теорема 6.5). Пусть точка C лежит внутри окружности. Прямая (BC) пересекает окружность в точке C 1 . Тогда четырехугольник A B C 1 D – вписанный в окружность и в соответствии с необходимым условием ∠ B A D + ∠ B C 1 D = 180 ˆ . Но ∠ B C D > ∠ B C 1 D как внешний к углу C 1 C D . Тогда ∠ B A D + ∠ B C D > ∠ B A D + ∠ B C 1 D , что противоречит условию. Следовательно, C лежит на окружности, и данный четырехугольник вписанный. Аналогично рассматривается случай, если предположить, что точка C лежит вне окружности. Теорема доказана.

Рис. 7.5.1. К теореме 7.13

Для того, чтобы выпуклый четырехугольник был описанным, необходимо и достаточно, чтобы суммы длин его противолежащих сторон были равны.

Необходимость. Пусть четырехугольник ABCD описанный, и M, P, L, N – точки касания его сторон. Имеем BM = BN, CM = CP, DP = DL, AL = AN (отрезки касательных, проведенных из одной точки равны). Отсюда BM + MC + AL + LD = BN + AN + CP +PD.

Достаточность. Пусть в четырехугольнике ABCD выполнено равенство AB + CD = BC + AD. Биссектрисы углов (BAD) и (ABC) пересекаются в точке O. Точка O одинаково удалена от прямых AB, BC и AD . Пусть ω (O, r) – окружность, касающаяся сторон AB, BC и AD, а сторона CD пересекает окружность ω. Проведем касательную к окружности ω из точки C, и пусть она пересекает прямую AD в точке D₁. Тогда из необходимого условия – AB + CD₁ = BC + AD₁. Вычитая из данного равенства равенство в условиях теоремы получаем CD₁ – CD = AD₁ – AD или CD₁ – CD = DD₁, CD₁ = CD + DD₁. Мы пришли к противоречию, так как CD₁

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Вписанные и описанные четырехугольники

Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности.
Очевидно, эта окружность будет называться описанной вокруг четырехугольника.

Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник.

На рисунке — вписанные и описанные четырехугольники и их свойства.

Ты нашел то, что искал? Поделись с друзьями!

Посмотрим, как эти свойства применяются в решении задач ЕГЭ.

. Два угла вписанного в окружность четырехугольника равны и . Найдите больший из оставшихся углов. Ответ дайте в градусах.

Сумма противоположных углов вписанного четырехугольника равна . Пусть угол равен . Тогда напротив него лежит угол в градусов. Если угол равен , то угол равен .

. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен .

Пусть сторона равна , равна , а . По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит,

Получается, что равна . Тогда периметр четырехугольника равен . Мы получаем, что , а большая сторона равна .

. Около окружности описана трапеция, периметр которой равен . Найдите ее среднюю линию.

Мы помним, что средняя линия трапеции равна полусумме оснований. Пусть основания трапеции равны и , а боковые стороны — и . По свойству описанного четырехугольника,
, и значит, периметр равен .
Получаем, что , а средняя линия равна .

Еще раз повторим свойства вписанного и описанного четырехугольника.

Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны .

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.

Докажите эти утверждения. Это задание особенно полезно тем, кто решает задачи второй части профильного ЕГЭ по математике.

Видео:вписанный и описанный четырехугольникСкачать

Доказать, что если четырехугольник является одновременно вписанным и описанным, то его площадь равна корню из произведения сторон?

Доказать, что если четырехугольник является одновременно вписанным и описанным, то его площадь равна корню из произведения сторон.

По формуле Брахмагупты площадь вписанного в окружность четырехугольника равна :

где a, b, c, d — стороны четырёхугольника, p — полупериметр.

Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны, т.

Уберём из формулы площади полупериметр, зная, что a + b = c + d :

$S = sqrt<(dfrac(a + b + c + d) — a)(dfrac(a + b + c + d) — b)> cdot \ \ sqrt<dfrac(a + b + c + d) — c)(dfrac(a + b + c + d) — d)> = \ \ sqrt<bigg(dfracbigg )^4(a + b + c -d)(a + b — c + d)(a — b+ c + d)(-a + b + c + d) > = \ \ sqrt<bigg(dfracbigg )^4(c + d + c -d)(c + d — c + d)(a — b+ a + b)(-a + b + a + b) >= \ \ sqrt< dfrac 2c cdot 2d cdot 2a cdot 2b > = sqrt< dfraccdot 16abcd > = boxed <sqrt>$.

Видео:2 ПРАВИЛА описанного четырехугольника #shortsСкачать

Сторона правильного четырехугольника равна 10 см?

Сторона правильного четырехугольника равна 10 см.

Найдите радиус окружности описанной около этого четырехугольника.

Видео:Описанные четырехугольники. 9 класс.Скачать

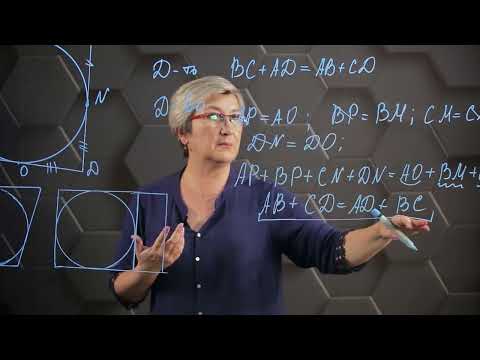
Как найти сторону описанного четырехугольника x + 4, если соседние стороны равны по 5 см?

Как найти сторону описанного четырехугольника x + 4, если соседние стороны равны по 5 см?

Как найти сторону описанного четырехугольника 2х, если соседние стороны равны по 5 см?

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Сторона правильного четырехугольника, описанного около некоторой окружности, равна 8?

Сторона правильного четырехугольника, описанного около некоторой окружности, равна 8.

Найдите площадь правильного треугольника, вписанного в эту окружность.

Видео:11 класс, 44 урок, Описанный четырехугольникСкачать

Найдите радиусы вписанной и описанной окружнотей около правильного четырехугольника со стороной 9 см?

Найдите радиусы вписанной и описанной окружнотей около правильного четырехугольника со стороной 9 см.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Сторона правильного треугольника описанного около окружности равна 12 корней из 3 Найдите сторону правильного шестиугольника вписанного в данную окружность?

Сторона правильного треугольника описанного около окружности равна 12 корней из 3 Найдите сторону правильного шестиугольника вписанного в данную окружность.

Видео:Вписанные четырехугольники. 9 класс.Скачать

Сторона квадрата равна 16 см?

Сторона квадрата равна 16 см.

Найди площади вписанной окружности в квадрате, и описанной.

Видео:11 класс, 43 урок, Вписанный четырехугольникСкачать

Как найти площадь квадрата описанного около окружности если площадь вписанного в эту окружность правильного 6 — ка равна 9 корней из 3?

Как найти площадь квадрата описанного около окружности если площадь вписанного в эту окружность правильного 6 — ка равна 9 корней из 3.

Видео:3 правила для вписанного четырехугольника #shortsСкачать

Сторона правильного треугольника равна 6 корней из 3?

Сторона правильного треугольника равна 6 корней из 3.

Вычислите площадь вписанного в него круга.

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Докажите, что площадь правильного шестиугольника равна утроенному произведению радиусов вписанной и описанной окружностей?

Докажите, что площадь правильного шестиугольника равна утроенному произведению радиусов вписанной и описанной окружностей.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Окружность радиуса 6 см вписана в четырехугольник, сумма противоположных сторон которого равна 28 см?

Окружность радиуса 6 см вписана в четырехугольник, сумма противоположных сторон которого равна 28 см.

Найдите площадь четырехугольника.

Видео:Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Сумма двух противоположных сторон описанного четырехугольника равна 13 см, а радиус вписанной в него окружности равен 9 см?

Сумма двух противоположных сторон описанного четырехугольника равна 13 см, а радиус вписанной в него окружности равен 9 см.

Найдите площадь четырехугольника.

На странице вопроса Доказать, что если четырехугольник является одновременно вписанным и описанным, то его площадь равна корню из произведения сторон? из категории Геометрия вы найдете ответ для уровня учащихся студенческий. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

По поводу третьей задачи. В условии явная ошибка. 2 — мя лучами угол нельзя разделить на 4 равных угла, только на 3 угла по 40 градусов. При этом невозможно получить суммированием ни одного угла по 60 градусов. Разделить на 4 равных угла можно то..

Если сторона треугольника, вписанного в окружность, совпадает с диаметром (проходит через центр окружности), то это значит, что треугольник прямоугольный. Из этого делаем вывод, что треугольник АВС — прямоугольный, а угол В — прямой. Исходя из этог..

Тк АС — диаметр = > угол В 90 градусов угол С = 180 — 90 — 81 = 9 градусов.

Угол EBC = BEA (как накрестлежащие) угол BAE = 180 — ABE — BEA = 180 — 62 — 62 = 56 (по правилу треугольника) BAE = BCD = 56 (по правилу параллелограмма) ABC = ABE + EBC = 62 + 62 = 124 ADC = ABC = 124 ОТВЕТ : BAE = ADC = 56, ABC = ADC = 124.

Х — первый угол, тогда х + 20 второй угол х + х + 20 = 180(сумма смежных углов 180) 2х = 160 х = 80 — первый угол 80 + 20 = 100 — второй угол.

Нарисуем трапецию и проведём высоте BM. Площадь трапеции равна полусумму оснований на высоту, а средняя линия трапеции равна полусумме оснований. Зная площадь трапеции и среднюю линию, найдём высоту. 180 : 45 = 4 Далее AM² = AB² — BM² = 25 — 16 = ..

1) Площадь поверхности шара (сферы) можно найти по формуле : Sсф = 4πR². 2) Для того, чтобы найти радиус шара, рассмотрим ΔОВА — прямоугольный, ОВ = 4 см, АВ = 3 см, по т. Пифагора ОА = R = √(ОВ² + АВ²) = = √(4² + 3²) = √(16 + 9) = √25 = 5 (см). 3..

АМ = МВ = 16 / 2 = 8 см МК = КВ = 8 / 2 = 4 см АК = АМ + МК = 8 + 4 = 12 см Ответ : 12 см.

С) т. К. у ромба перпендикулярные диагонали, а не у прямоугольника.

🌟 Видео

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

ОГЭ Задание 25 Свойства вписанного и описанного четырехугольникаСкачать

Геометрия 11 класс. Вписанный четырехугольникСкачать

ГЕОМЕТРИЯ ОГЭ ЕГЭ. ЧЕТЫРЕХУГОЛЬНИКИ ВПИСАННЫЕ И ОПИСАННЫЕСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать