- Задача
- Подсказка
- Решение
- Послесловие
- Доказательство
- Решение головоломки
- Правильный шестиугольник и его свойства
- Определение и построение
- Свойства простые и интересные
- Описанная окружность и возможность построения
- Вписанная окружность
- Периметр и площадь
- Занимательные построения
- От теории к практике
- Правильный шестиугольник и его свойства
- 🎦 Видео
Видео:Геометрия - Построение шестиугольникаСкачать

Задача
Правильный шестиугольник со стороной n разбит на единичные треугольники. Отметим все вершины этих треугольников. Найдите:
а) количество правильных шестиугольников с вершинами в отмеченных точках, стороны которых лежат на линиях разбиения (как оранжевый шестиугольник на рис. 1);
б) количество всех правильных шестиугольников с вершинами в отмеченных точках.
Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Подсказка
а) Начните с небольших n = 1, 2, 3, … Постарайтесь заметить закономерность в последовательности чисел, равных количеству шестиугольников в каждом случае.
б) Рассмотрите частный случай: выясните, сколько шестиугольников определяют точки, расположенные на периметре правильного шестиугольника со стороной m, и, учитывая результат пункта а), найдите общее число всех шестиугольников.
Видео:Шестиугольник в изометрииСкачать

Решение
а) Итак, рассмотрим правильный шестиугольник H со стороной n, нарисованный на треугольной сетке. Посчитаем, сколько в нем содержится правильных шестиугольников со сторонами, параллельными сторонам H.
Ясно, что шестиугольник со стороной n всего один — он совпадает с H. Шестиугольников со стороной (n-1) уже 7 штук: у одного центр совпадает с центром H, а остальные получаются из него сдвигами к каждой из вершин H. Если продолжить уменьшать размер шестиугольника, то после аккуратного разбора случаев можно получить, что со стороной (n-2) будет 19 шестиугольников, а со стороной (n-3) — уже 37. Как возникают эти числа и что их объединяет?
Зафиксируем натуральное (k 
Поскольку у каждого шестиугольника ровно одна левая нижняя вершина, то получается, что всего таких шестиугольников будет столько же, сколько узлов сетки попадает внутрь и на стороны шестиугольника со стороной (n-k).
Считать число точек внутри шестиугольника с данной стороной m можно разными способами. Мы последуем простому и изящному рассуждению, приведенному Мартином Гарднером в книге «Путешествие во времени». На рис. 3 все точки разбиты на четыре группы: те, что находятся в трех параллелограммах, плюс одна центральная точка. В одном параллелограмме (m(m-1)) точек, поэтому всего в шестиугольнике со стороной m будет (p_m=3m(m-1)+1=3m^2-3m+1) точек.
Нам, чтобы теперь решить задачу, нужно просуммировать эти выражения по всем m от 1 до n, то есть найти сумму (P=sumlimits_^n p_m). Удобнее всего это сделать, перегруппировав слагаемые так, чтобы отдельно сложить квадраты, отдельно — первые степени и отдельно — единицы:
Теперь осталось воспользоваться известными формулами для суммы чисел от 1 до n и для суммы их квадратов (см. задачу Суммы квадратов, суммы кубов. ):
После упрощения получится, что это выражение равно (n^3).
б) Надо заметить, что все точки, расположенные на периметре правильного шестиугольника со стороной m (где (minmathbb), (mle n)) определяют ровно m правильных шестиугольников (рис. 4). Верно и обратное: если на нашей сетке построен правильный шестиугольник, то его вершины обязательно будут лежать на сторонах другого шестиугольника, которые при этом параллельны сторонам H.
С учетом результатов пункта а) это означает, что надо найти сумму (N=sumlimits_^(p_cdot m)). Или, в полном виде:
Упрощать это выражение можно по-разному. Вот один из путей. Сначала выделим в отдельное слагаемое сумму, которую мы уже нашли в пункте а):
Сумма в первых скобках равна, как мы знаем, (n^3), и с учетом множителя n получится (n^4).
Разберемся со второй суммой. Компактно она записывается в виде (sumlimits_^ p_mcdot (m-1)). Но каждое слагаемое ( p_mcdot (m-1)=(3m^2-3m+1)(m-1)=3m^3-6m^2+4m-1) — это многочлен, а значит с этой суммой можно поступить так же, как мы делали в пункте а) — перегруппировать ее так, чтобы каждая степень складывалась отдельно:
Опять воспользуемся известными формулами для этих сумм и получим:
После упрощения останется следующее: (frac34n^4-frac12n^3-frac14n^2).
Поэтому искомое число всех правильных шестиугольников равно:
Видео:Как построить правильный шестиугольник.Скачать

Послесловие
Ненадолго отвлечемся от треугольных решеток и рассмотрим довольно естественно возникающий в контексте этой задачи вопрос: можно ли на обычной квадратной сетке (на построить правильный шестиугольник или треугольник так, чтобы все его вершины находились в узлах?
Оказывается, что нет. Краткое доказательство приводится ниже в скрытом виде, так что у вас остается возможность подумать самостоятельно над тем, почему это так.
Доказательство
Поскольку взятые через одну вершины правильного шестиугольника образуют правильный треугольник, то достаточно доказать, что не существует правильного треугольника с вершинами в узлах обычной квадратной решетки.
Допустим, что такой треугольник ABC все-таки существует. Тогда его площадь обязательно выражается рациональным числом. Это сразу следует из формулы Пика (см. статью Г. Мерзона Площади многоугольников и тающий лёд), но есть и простое наглядное рассуждение, не привлекающее такую «тяжелую артиллерию». Дело в том, что треугольник ABC достраивается до прямоугольника AMNK (достаточно провести через его вершины вертикальные и горизонтальные линии сетки, см. рис), площадь которого, очевидно, целая. При этом добавляются три прямоугольных треугольника (или два, если одна из сторон треугольника ABC идет по линии сетки), площади S1, S2 и S3 которых либо целые, либо полуцелые. Значит, и площадь треугольника ABC сама тоже либо целая, либо полуцелая — и в любом случае рациональная.
С другой стороны, площадь правильного треугольника выражается через его сторону AB по формуле (AB^2sqrt3/4). Но по теореме Пифагора (AB^2=AM^2+MB^2) — целое число. Поскольку (sqrt3) — число иррациональное, то и площадь получается иррациональной. Получаем противоречие: одно и то же число (площадь ABC) не может быть одновременно рациональным и иррациональным.
Можно рассуждать и несколько по-другому. А именно, следить можно не за площадями, а за углами треугольника. Точнее, за их тангенсами. С одной стороны, как хорошо известно, угол равностороннего треугольника равен 60°, а его тангенс — (sqrt3). С другой стороны, аналогичным достроением до прямоугольника получим, что этот угол представляется как сумма (или разность — в зависимости от расположения треугольника ABC относительно линий сетки) двух углов, тангенсы которых рациональны. Из этого следует, что и этот угол должен быть рациональным (см. формулу тангенса суммы). Опять получается противоречие.
Вернемся к треугольной решетке. При внимательном ее рассмотрении обнаруживаются интересные свойства. Например, в каждом правильном шестиугольнике с вершинами в узлах решетки центр тоже является узлом. Кажется, что это очень простое наблюдение, но оно позволяет заметить большее. Оказывается, что число шестиугольников, имеющих центром некоторый узел, в точности равно значению выражения (h(h+1)/2), где h — расстояние от этого узла до ближайшей стороны исходного шестиугольника, а в качестве единицы измерения взята высота единичного треугольника сетки (рис. 5).
Это легко можно доказать, опираясь на факт, которым мы пользовались при решении пункта б): с центром в данном узле существует ровно h шестиугольников размера от 1 до h, стороны которых параллельны сторонам исходного шестиугольника H, а каждый из них «порождает», в соответствии с упомянутым фактом, число шестиугольников, равное его размеру. Значит, надо сложить числа от 1 до h, а это и даст выражение (h(h+1)/2). Числа такого вида называют треугольными.
Опираясь на эту находку, сделанную Сергеем Царановым, можно решить пункт б) еще одним способом. Для этого в каждом внутреннем узле решетки запишем число, равное количеству шестиугольников, имеющих центром данный узел (рис. 6, слева) — то есть соответствующее треугольное число Tk. Сумма всех записанных чисел будет равна числу всех правильных шестиугольников (будут посчитаны и те шестиугольники, стороны которых не лежат на линиях разбиения).
Но как сосчитать такую сумму? Можно так: все слагаемые разобьем на 6 одинаковых групп, заключенные в треугольные области, тогда искомая сумма равна увеличенной в 6 раз сумме всех чисел одной группы и плюс центральное число, не вошедшее ни в одну из групп (рис. 6, справа), которое равно Tn. Учитывая, что в группе по рядам записаны треугольные числа, получаем, что нужно посчитать сумму (sumlimits_^(T_icdot (n-i))). Это делается аналогично тому, как подсчитывались суммы в решении — получится (frac(n-1)n(n+1)(n+2)).
Значит, всего шестиугольников
Упрощая это выражение получим все тот же результат — (left(fracright)^2). Это, кстати, квадрат центрального треугольного числа.
Другой подход есть и к пункту а), причем он почти не требует вычислений. По аналогии с рис. 2 будем отмечать положения, которые может занимать центр шестиугольника (со сторонами, параллельными сторонам исходного шестиугольника), последовательно уменьшая его размер от n до 1 (рис. 7).
То есть для каждого размера мы имеем свое множество центров. Каждое из этих множеств можно представить себе по-другому: в виде трехгранного уголка, сложенного из единичных кубиков (рис. 8). Из таких уголков складывается кубик со стороной n. Это и дает ответ: n 3 шестиугольников.
С обсуждаемой задачей связана и придуманная автором головоломка «Разрушенные шестиугольники»: из спичек сложен правильный шестиугольник, разбитый на треугольные ячейки (рис. 9); какое наименьшее количество спичек надо убрать из этой конструкции, чтобы в ней не осталось ни одного контура правильного шестиугольника?
Попробуйте решить ее самостоятельно, опираясь на уже известные сведения о числе шестиугольников.
Решение головоломки
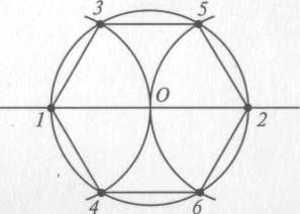
Как мы уже знаем, в шестиугольнике со стороной 3 есть 27 правильных шестиугольников: 19 со стороной 1 спичка, 7 со стороной 2 спички и 1 со стороной 3 спички. Заметим, что шесть спичек — по одной при каждой вершине исходного шестиугольника — не входят ни в один из этих 27 шестиугольников, поэтому ни одну из этих спичек нет смысла убирать.
Остальные спички можно представить в объединения трех неперекрывающихся групп спичек. В первой группе 6 шестиугольников со стороной 1 спичка, во второй группе 7 таких шестиугольников, в третьей группе — еще 6 (см. рис.).
Чтобы разрушить эти 19 шестиугольников, надо разбить их на смежные пары и в каждой паре убрать общую спичку, то есть надо убрать 3 + 4 + 3 = 10 спичек. После чего останется только один центральный шестиугольник со стороной 2, для разрушения которого надо убрать еще одну спичку. Значит, всего требуется убрать 11 спичек — например так, как показано на следующем рисунке.
Эта головоломка основана на исходной задаче при n = 3. При n = 1 и n = 2 она решается совсем просто, а вот уже при n = 4 возникают сложности и без компьютерного перебора справиться не получается. Возможно, у кого-то из читателей получится это сделать.
Видео:Как сделать правильный шестиугольник из бумагиСкачать

Правильный шестиугольник и его свойства

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
чертится прямая линия и на ней ставится точка;
- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Видео:Шестиугольник - гексагон за 1 минуту ! Без циркуля и заморочек ! Сможет даже ребёнок .Скачать

Свойства простые и интересные
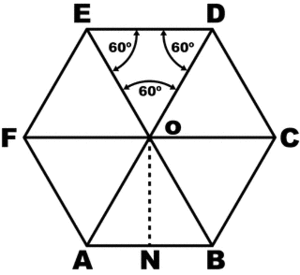
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
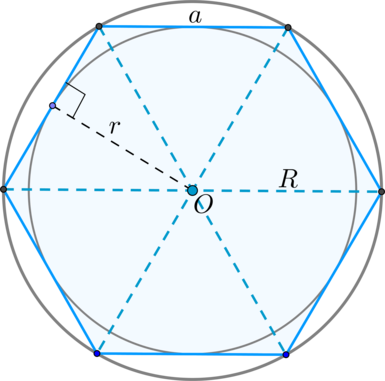
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
R=а.
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
S=πR²
Вписанная окружность
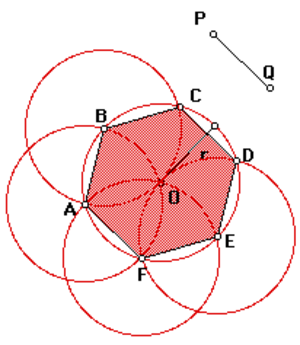
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
Видео:Построение правильного шестиугольника при помощи циркуля и линейкиСкачать

От теории к практике
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Видео:🔥 ФОКУС с треугольником #shortsСкачать

Правильный шестиугольник и его свойства
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac 4cdot 180^circ=90^circ) ;
каждый угол правильного шестиугольника равен (dfrac6cdot 180^circ=120^circ) .
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfracn\ r&=Rcdot cosdfracn end]
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: (a=R) .
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны (120^circ) .
4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt>a^2) .
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac) .
🎦 Видео
Построение медианы в треугольникеСкачать

Построение высоты в треугольникеСкачать

ВНЕШНИЕ УГЛЫ ТРЕУГОЛЬНИКА 😉 #shorts #математика #егэ #огэ #профильныйегэСкачать

Как поделить окружность на 3 равные части. Очень просто. Уроки черчения.Скачать

Построение пятиугольника циркулемСкачать

Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Осевая симметрия, как начертить треугольники симметричноСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Сравнение углов. Виды углов. Чертежный треугольник. 5 класс.Скачать

ТЕМА 5. ПОСТРОЕНИЕ ШЕСТИГРАННОЙ ПРИЗМЫ, КОНУСА И ЧЕТЫРЕХГРАННОЙ ПИРАМИДЫ.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать













 чертится прямая линия и на ней ставится точка;
чертится прямая линия и на ней ставится точка;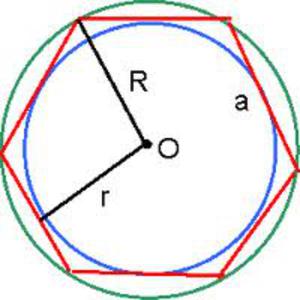 Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.