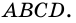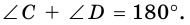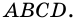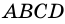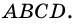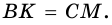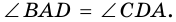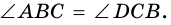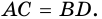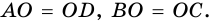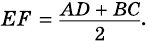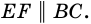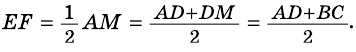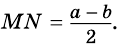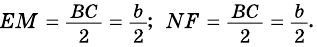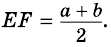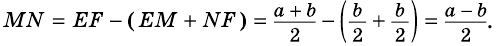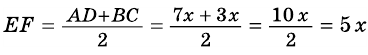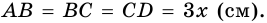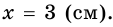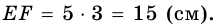Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение четырехугольника
- Выпуклые четырехугольники
- Параллелограмм
- Определение четырехугольника
- Выпуклые четырехугольники
- Параллелограмм
- Прямоугольник
- Квадрат
- Трапеция
- Примеры решений заданий из ОГЭ
- Трапеция и ее свойства с определением и примерами решения
- Свойства трапеции
- Свойства равнобокой трапеции
- Свойство средней линии трапеции
- Решение на Упражнение 1286 из ГДЗ по Математике за 6 класс: Мерзляк А.Г.
- Условие
- Решение 1
- Решение 2
- Популярные решебники
- 💡 Видео
Видео:8 класс, 4 урок, ПараллелограммСкачать

Определение четырехугольника
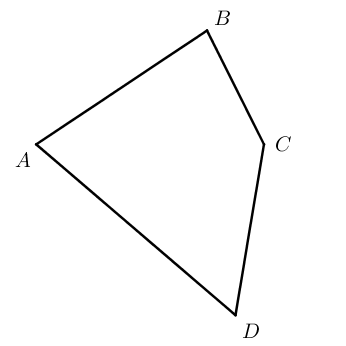
Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырехугольники бывают выпуклые ( A B C D ) и невыпуклые ( A 1 B 1 C 1 D 1 ) .
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Выпуклые четырехугольники
В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.
Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: A B и A D , A B и B C , B C и C D , C D и A D .
Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: A B и C D , B C и A D .
Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C , B и D .
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. A C и B D – диагонали четырехугольника A B C D .
Диагонали выпуклого четырехугольника пересекаются в одной точке.
Площадь произвольного выпуклого четырехугольника можно найти по формуле:
S = 1 2 d 1 d 2 ⋅ sin φ
где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).
Рассмотрим более подробно некоторые виды выпуклых четырехугольников.
Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.
Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Параллелограмм
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма:
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180 ° .
- Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )
Площадь параллелограмма можно найти по трём формулам.
Как произведение стороны и высоты, проведенной к ней.
Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.
Как произведение двух смежных (соседних) сторон на синус угла между ними.
Как полупроизведение диагоналей на синус угла между ними.
Ромб – параллелограмм, у которого все стороны равны.
Свойства ромба:
- Диагонали пересекаются под прямым углом.
- Диагонали являются биссектрисами углов, из которых выходят.
- Сохраняются все свойства параллелограмма.
Площадь ромба можно найти по трём формулам.
Как произведение стороны ромба на высоту ромба.
Как квадрат стороны ромба на синус угла между двумя сторонами.
Как полупроизведение диагоналей ромба.
Видео:ГЕОМЕТРИЯ 8 класс: Трапеция (что это такое, признаки и свойства) | ВидеоурокСкачать

Прямоугольник
Прямоугольник – это параллелограмм, у которого все углы равны 90 ° .
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Сохраняются все свойства параллелограмма.
Площадь прямоугольника можно найти по двум формулам:
Как произведение двух смежных (соседних) сторон прямоугольника.
Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.
Видео:№52. Две стороны треугольника параллельны плоскости α. Докажите, что и третья сторонаСкачать

Квадрат
Квадрат – прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Сохраняет свойства ромба.
- Сохраняет свойства прямоугольника.
Площадь квадрата можно вычислить по двум формулам:
Как квадрат стороны.
Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).
Видео:Какие бывают четырехугольники?Скачать

Трапеция
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.
Стороны, которые параллельны друг другу называются основаниями , другие две стороны называются боковыми сторонами .
B C и A D – основания, A B и C D – боковые стороны трапеции A B C D .
Свойства трапеции:
сумма углов, прилежащих к боковой стороне, равна 180 ° .
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2
Площадь трапеции можно найти по двум формулам:
Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.
Как полупроизведение диагоналей на синус угла между ними.
Виды трапеций
Прямоугольная трапеция – трапеция, у которой два угла прямые.
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.
Свойство равнобокой трапеции: углы при основании равны
Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с четырехугольниками
Видео:8 класс, 6 урок, ТрапецияСкачать

Трапеция и ее свойства с определением и примерами решения
Содержание:
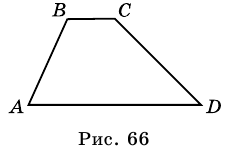
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
На рисунке 66 изображена трапеция
Видео:ОГЭ ЗАДАНИЕ 15 ГЕОМЕТРИЯ 1 ЧАСТЬ РАВНОБЕДРЕННАЯ ТРАПЕЦИЯСкачать

Свойства трапеции
Рассмотрим некоторые свойства трапеции.
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.
Так как 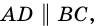
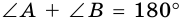
2. Трапеция является выпуклым четырехугольником.
Поскольку 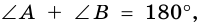
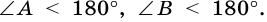
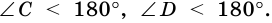
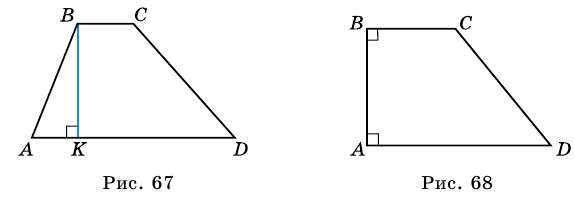
Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.
Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 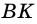
Трапецию называют прямоугольной, если один из ее углов -прямой. На рисунке 68 — прямоугольная трапеция 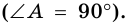
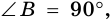
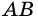
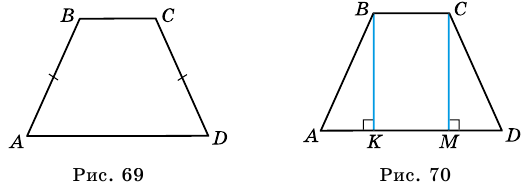
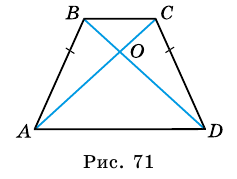
Трапецию называют равнобокой, если ее боковые стороны равны. На рисунке 69 — равнобокая трапеция
Видео:Четырехугольники или все что нужно знать о трапеции на ОГЭ. Задание номер 17Скачать

Свойства равнобокой трапеции
Рассмотрим некоторые важные свойства равнобокой трапеции.
1. В равнобокой трапеции углы при основании равны.
Доказательство:
1) Пусть в трапеции 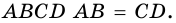
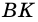
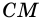
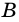
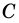
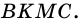
2) 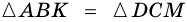
3) Также 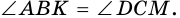
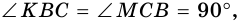
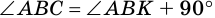
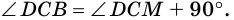
2. Диагонали равнобокой трапеции равны.
Доказательство:
Рассмотрим рисунок 71. 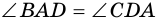
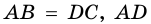
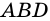
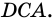
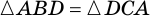
Пример:
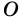
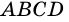
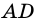
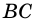
Доказательство:
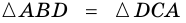
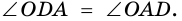
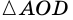
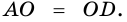
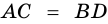
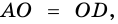
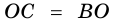
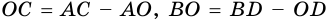
Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.
Доказательство:
1) Пусть в 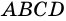
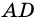
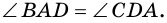
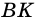
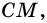
2) Тогда 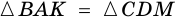
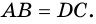
Термин «трапеция» греческого происхождения (по-гречески «трапед-зион» означает «столик», в частности столик для обеда; слова «трапеция» и «трапеза» — однокоренные).
В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.
Трапеция в современной трактовке впервые встречается у древнегреческого математика Посидония (I в.), но начиная только с XVIII в. этот термин стал общепринятым для четырехугольников, у которых две стороны параллельны, а две другие — не параллельны.
Видео:Трапеция, решение задач. Вебинар | МатематикаСкачать

Свойство средней линии трапеции
Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.
Рассмотрим свойство средней линии трапеции.
Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 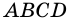
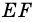
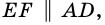
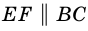
1) Проведем луч 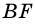
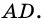
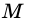
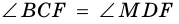
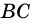
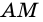
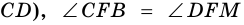
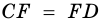
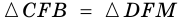
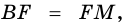
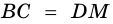
2) Поскольку 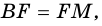
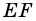
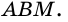
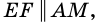
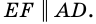
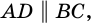
3) Кроме того,
Пример:
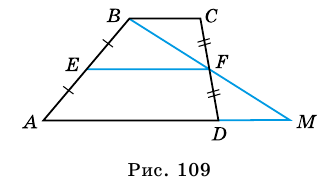
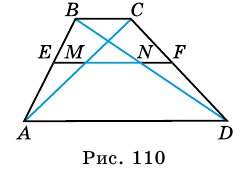
Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.
Доказательство:
Пусть 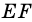
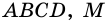
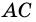
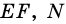
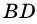
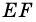
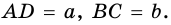
1) Так как 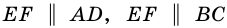
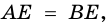
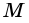
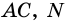
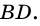
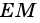
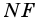
Тогда
2) 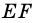
3)
Пример:
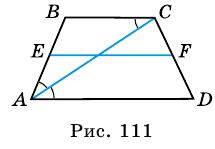
В равнобокой трапеции диагональ делит острый угол пополам. Найдите среднюю линию трапеции, если ее основания относятся как 3 : 7, а периметр трапеции — 48 см.
Решение:
Пусть 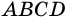
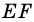
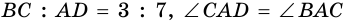
1) Обозначим 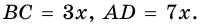
2) 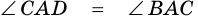
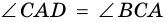
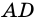
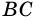
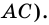
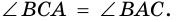
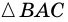
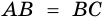
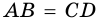
3) Учитывая, что 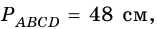
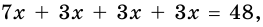
4) Тогда
То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).
О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Площадь трапеции
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Площадь параллелограмма
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Многострадальная задача про кривую трапецию. 8-9 класс | МатематикаСкачать

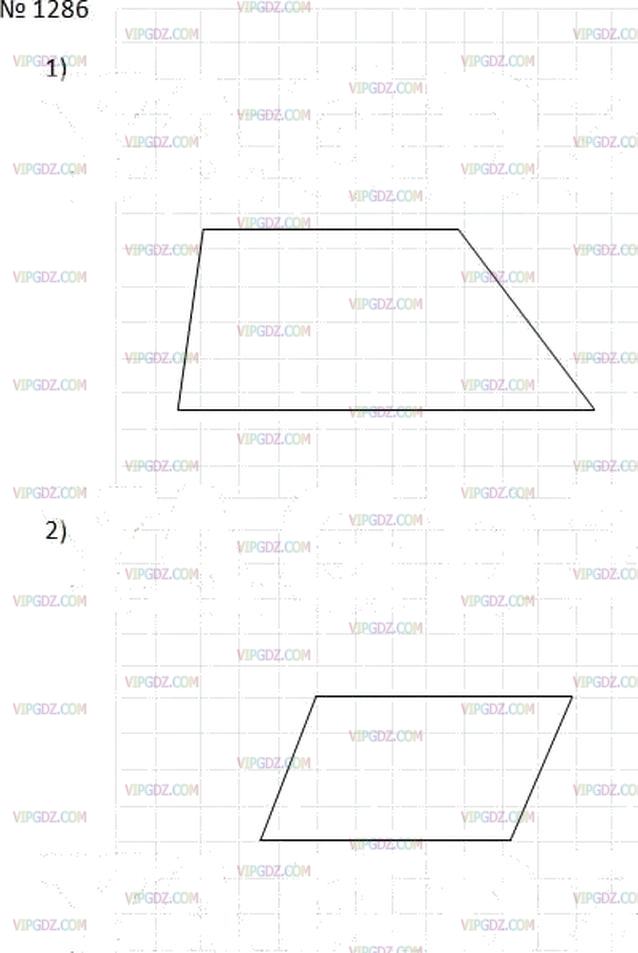
Решение на Упражнение 1286 из ГДЗ по Математике за 6 класс: Мерзляк А.Г.
Условие
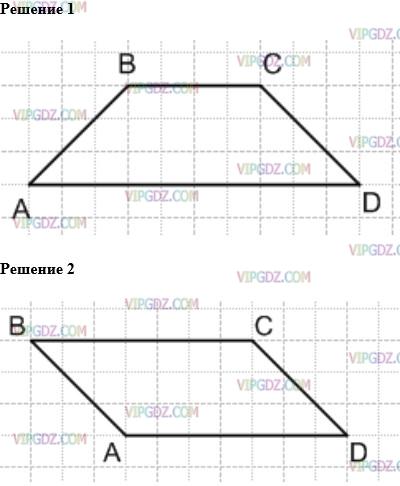
Решение 1
Решение 2
Поиск в решебнике
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Популярные решебники
Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. — 2013г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015г.
💡 Видео
Задача про А и ВСкачать

четырехугольники в огэ по математике 2023 / маттаймСкачать

СРЕДНЯЯ ЛИНИЯ. ТРАПЕЦИЯ. ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. Контрольная № 2 Геометрия 8 классСкачать

Задача на вычисление площади трапецииСкачать

В СССР такую задачу решали 2 человека Я и ты, но ты лучшеСкачать

Геометрия 8 класс - ТЕОРИЯ: Многоугольник. Четырёхугольник. Вычисление ПЛОЩАДИ Четырёхугольников (1)Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать