Четырехугольник авсд вписан в окружность р точка пересечения продолжений сторон ав и сд

Геометрия | 5 — 9 классы

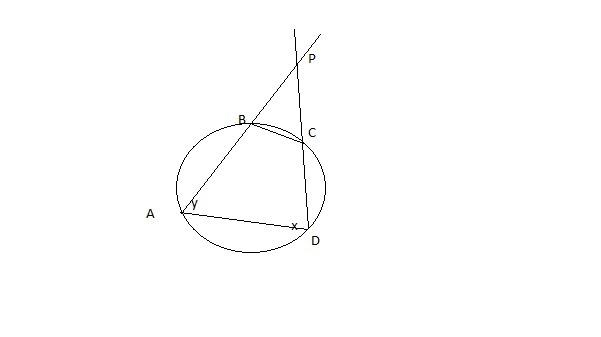
Четырёхугольник ABCD вписан в окружность, P — точка пересечения продолжений сторон AB и CD.

Докажите, что AP * BP = CP * DP.

Пусть ∠BAD = y, ∠CDA = x.

Тогда по свойству вписанного четырехугольника имем :

∠BAD + ∠BCD = 180⇒ ∠BCD = 180 — y,

∠CDA + ∠ABC = 180⇒ ∠ABC = 180 — x.

∠ABC и ∠PBC — смежные, значит, ∠PBC = 180 — ∠BCD = 180 — 180 + x = x.

∠BCD и ∠BCP — смежные, значит, ∠BCP = 180 — ∠BCD = 180 — 180 + y = y.

∠P — общий для треугольников BPC и ABP, а два других угла равны⇒ треугольники подобны.

Из подобия следует, что AP / CP = DP / BP⇔ AP * BP = CP * DP.

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Четырёхугольник ABCD вписан в окружность?

Четырёхугольник ABCD вписан в окружность.

Видео:Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать

В четырёхугольник ABCD вписана окружность, AB = 8, CD = 30?

В четырёхугольник ABCD вписана окружность, AB = 8, CD = 30.

Найдите периметр четырёхугольника.

У четырёхугольника все стороны разные.

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K?

Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K.

Докажите, что треугольники KAB и KCD подобны.

Видео:#29. Регион ВсОШ 2023, 9.5Скачать

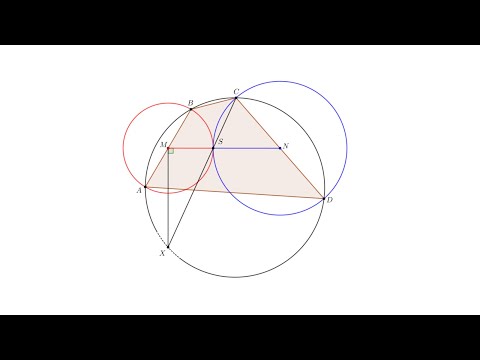
Четырёхугольник ABCD вписан в окружность, P — точка пересечения продолжений сторон AB и CD?

Четырёхугольник ABCD вписан в окружность, P — точка пересечения продолжений сторон AB и CD.

Докадите, что AP * BP = CP * DP.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Помогите пожалуйста решить)Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K?

Помогите пожалуйста решить)

Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K.

Докажите, что треугольники KAB и KCD подобны.

Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

В четырёхугольнике ABCD вписана окружность , AB = 7 ВС = 13 и СD = 11?

В четырёхугольнике ABCD вписана окружность , AB = 7 ВС = 13 и СD = 11.

Найдите четвёртую сторону четырёхугольника.

Видео:Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

В четырёхугольник ABCD вписана окружность, АВ = 8, ВС = 7 и СД = 31?

В четырёхугольник ABCD вписана окружность, АВ = 8, ВС = 7 и СД = 31.

Найдите четвёртую сторону четырёхугольника.

Видео:ОГЭ ЗАДАНИЕ 16 ЧЕТЫРЕХУГОЛЬНИК АВСД ВПИСАН В ОКРУЖНОСТЬ. НАЙДИТЕ УГОЛ АБДСкачать

Четырёхугольник ABCD со сторонами AB = 34 и CD = 22 вписан в окружность?

Четырёхугольник ABCD со сторонами AB = 34 и CD = 22 вписан в окружность.

Диагонали AC и BD пересекаются в точке K , причём ∠AKB = 60° Найдите радиус окружности, описанной около этого четырёхугольника.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

В четырёхугольнике ABCD вписана окружность, AB = 10, BC = 6, CD = 16?

В четырёхугольнике ABCD вписана окружность, AB = 10, BC = 6, CD = 16.

Найдите четвёртую сторону четырёхугольника.

Видео:2122 в четырёхугольник ABCD вписана окружностьСкачать

В четырёхугольник Abcd вписана окружность, ab = 7, CB = 13 и cd = 11?

В четырёхугольник Abcd вписана окружность, ab = 7, CB = 13 и cd = 11.

Найдите четвёртую сторону четырёхугольника.

Вы зашли на страницу вопроса Четырёхугольник ABCD вписан в окружность, P — точка пересечения продолжений сторон AB и CD?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Пусть∠1 = 2х, ∠2 = 3х ∠1 + ∠2 = 180°⇒2х + 3х = 5х = 180°⇒х = 36°⇒∠1 = 2 * 36° = 72°, ∠2 = 3 * 36° = 108°.

Видео:ОГЭ по математике. Задание 15Скачать

Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность

С разделением математики на алгебру и геометрию учебный материал становится сложнее. Появляются новые фигуры и их частные случаи. Для того чтобы хорошо разобраться в материале, необходимо изучить понятия, свойства объектов и сопутствующие теоремы.

Видео:Четырехугольник АВСD со сторонами АВ=12 иСD=13 вписан в окружность. 27 вариант Ященко ОГЭ задача 25Скачать

Общие понятия

Под четырехугольником подразумевается геометрическая фигура. Состоит она из 4-х точек. Причем 3 из них не располагаются на одной прямой. Имеются отрезки, последовательно соединяющие указанные точки.

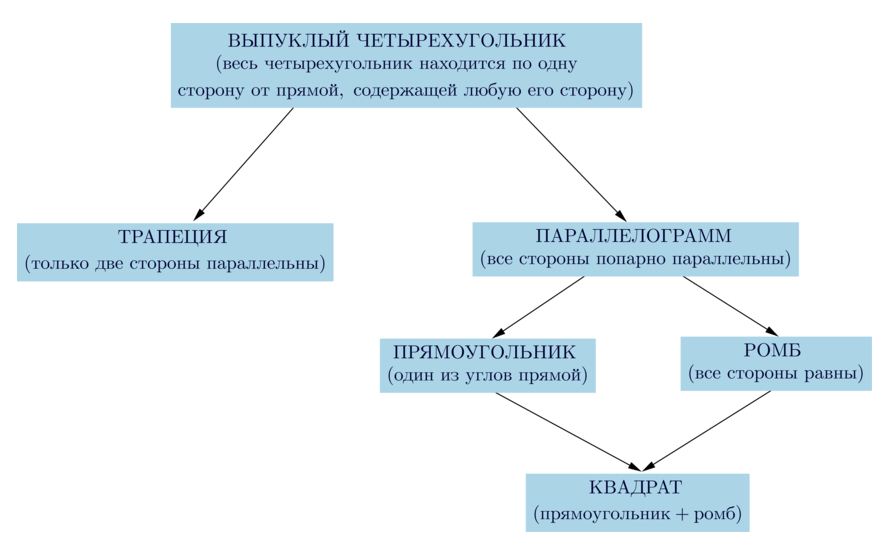
Все четырехугольники, изучаемые в школьном курсе геометрии, показаны в следующей схеме. Вывод: любой объект из представленного рисунка обладает свойствами предыдущей фигуры.

Четырехугольник может быть следующих видов:

• Параллелограмм. Параллельность его противоположных сторон доказывается соответствующими теоремами.
• Трапеция. Четырехугольник, у которого основания параллельны. Другие две стороны – нет.
• Прямоугольник. Фигура, у которой все 4 угла = 90º.
• Ромб. Фигура, у которой все стороны равны.
• Квадрат. Совмещает в себя свойства последних двух фигур. У него все стороны равны и все углы прямые.

Основное определение данной темы – вписанный четырехугольник в окружность. Оно заключается в следующем. Это фигура, вокруг которой описана окружность. Она должна проходить через все вершины. Внутренние углы четырехугольника, вписанного в окружность, в сумме дают 360º.

Не каждый четырехугольник может быть вписан. Связано это с тем, что серединные перпендикуляры 4-х сторон могут не пересечься в одной точке. Это сделает невозможным нахождение центра окружности, описанной около 4-угольника.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Частные случаи

Из всякого правила есть исключения. Так, в данной теме также имеются частные случаи:

• Параллелограмм, как таковой, не может быть вписан в окружность. Только его частный случай. Это прямоугольник.
• Если все вершины ромба находятся на описывающей линии, то он является квадратом.
• Все вершины трапеции находятся на границе окружности. В таком случае говорят о равнобедренной фигуре.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Свойства вписанного четырехугольника в окружность

Перед решением простых и сложных задач по заданной теме необходимо удостовериться в своих знаниях. Без изучения учебного материала невозможно решить ни один пример.

Видео:#МАТЕМАТИКА #ОГЭ-2023 || Вариант №1 на 4 || 15 балловСкачать

Теорема 1

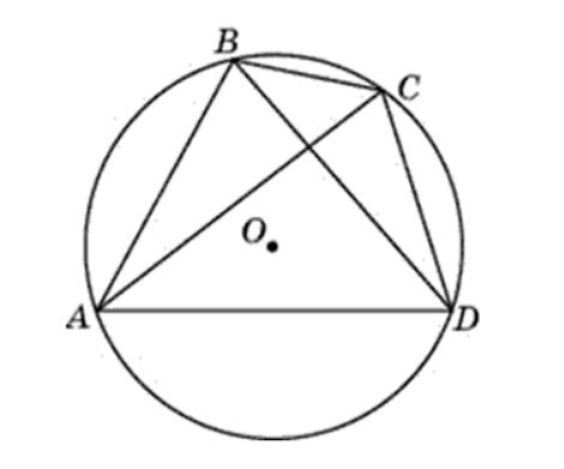
Сумма противоположных углов, четырехугольника вписанного в окружность, равна 180º.

Дано: четырехугольник АВСД вписан в окружность. Ее центр – точка О. Нужно доказать, что _{18 ноября, 2018}

Видео:ВСЯ ГЕОМЕТРИЯ ЗА 30 МИНУТСкачать

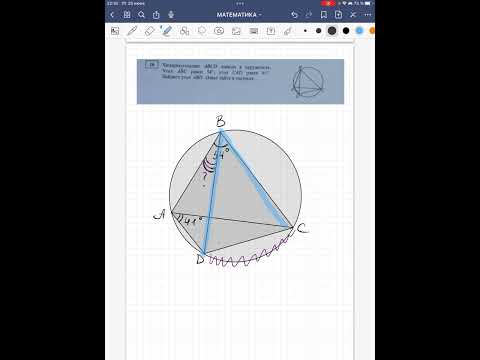
Продолжения сторон ab и cd четырехугольника abcd вписанного в окружность пересекаются в точке p. Градусная

мера меньшей дуги окружности, стягиваемой хордой bc равно 40, а градусная мера меньшей дуги, стягиваемой хордой ad, равно 130. найдите градусную меру угла apd.

1) Проведём BD. Получим вписанные углы. ∠ABD = 65° ( опирается на дугу 130° и равен её половине)

2) ∠РВD = 180° — 65° = 115° (как смежный с ∠ABD)

3) ∠BDC = 20° ( ( опирается на дугу 40° и равен её половине)

∠ P = 180° — (115° + 20°) = 180° — 135° = 45°

🌟 Видео

Четырёхугольник ABCD вписан в окружность причём BC CD Известно что угол ADC равен 93Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Задача 6 №27876 ЕГЭ по математике. Урок 117Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать