Видео:+Как найти длину окружностиСкачать

Свойства
Поскольку радиус конуса характеризует размер его основания, то зная его, можно найти диаметр, длину окружности и площадь круга, лежащего в основании. Диаметр представляет собой удвоенный радиус, длина окружности – удвоенный радиус, умноженный на число π, а площадь круга – квадрат радиуса, умноженный на число π. d=2r P=2πr S_(осн.)=πr^2
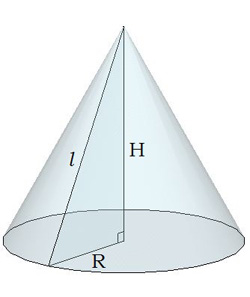
Зная радиус и образующую конуса, можно уже найти его высоту, угол между образующей и основанием, угол раствора конуса. Высота конуса через радиус и образующую ищется по теореме Пифагора в прямоугольном треугольнике, оттуда же можно вычислить и угол β через тригонометрические отношения сторон. Угол α можно найти из равнобедренного треугольника, образованного двумя образующими и диаметром, отняв из 180 градусов два угла β. (рис.40.1, 40.2) h=√(l^2-r^2 ) cosβ=r/l α=180°-2β
Площадь боковой поверхности конуса равна произведению полупериметра основания на образующую или произведению числа π на радиус и образующую. Чтобы найти площадь полной поверхности, зная радиус и образующую конуса, необходимо прибавить к площади боковой поверхности произведение числа π на квадрат радиуса, что является площадью основания конуса. S_(б.п.)=πrl S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)
Объем конуса, также как и объем пирамиды рассчитывается как одна треть основания, умноженная на высоту. V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, вычисляется как произведение высоты на радиус конуса, деленное на сумму радиуса и образующей. Радиус сферы, описанной вокруг конуса, представляет собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4) r_1=hr/(l+r)=(r√(l^2-r^2 ))/(l+r) R=l^2/2h
Видео:Длина окружности. Математика 6 класс.Скачать

Задание №3 Длина окружности основания конуса
| Длина окружности основания конуса равна 18πсм, высота конуса равна 4,5см. Вычислить объём конуса. | |
 | Дано: С окружности= 18πсм Hконуса=4,5см Найти: Vконуса-? |
Решение: Длину окружности основания конуса можно вычислить по формуле c=2πR. Вычислим радиус основания конуса R= 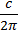 = = 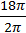 =9см Вычислим объём конуса V=πR 2 =9см Вычислим объём конуса V=πR 2  = = 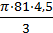 =121,5πсм 3 Ответ: V(конуса)= 121,5πсм 3 =121,5πсм 3 Ответ: V(конуса)= 121,5πсм 3 | |
| Решить задание на ЯКласс | №3 Длина окружности основания конуса |
Задание №4 Высота усечённого конуса
Площади оснований усечённого конуса равны 4πсм 2 и 36π см2; объём равен 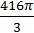 см 3 . Вычислить высоту усечённого конуса. см 3 . Вычислить высоту усечённого конуса. | |
Дано: S1= 4πсм 2 S2= 36πсм 2 V усеч.конуса= 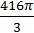 см 3 . Найти: Hконуса-? см 3 . Найти: Hконуса-? | |
Решение: 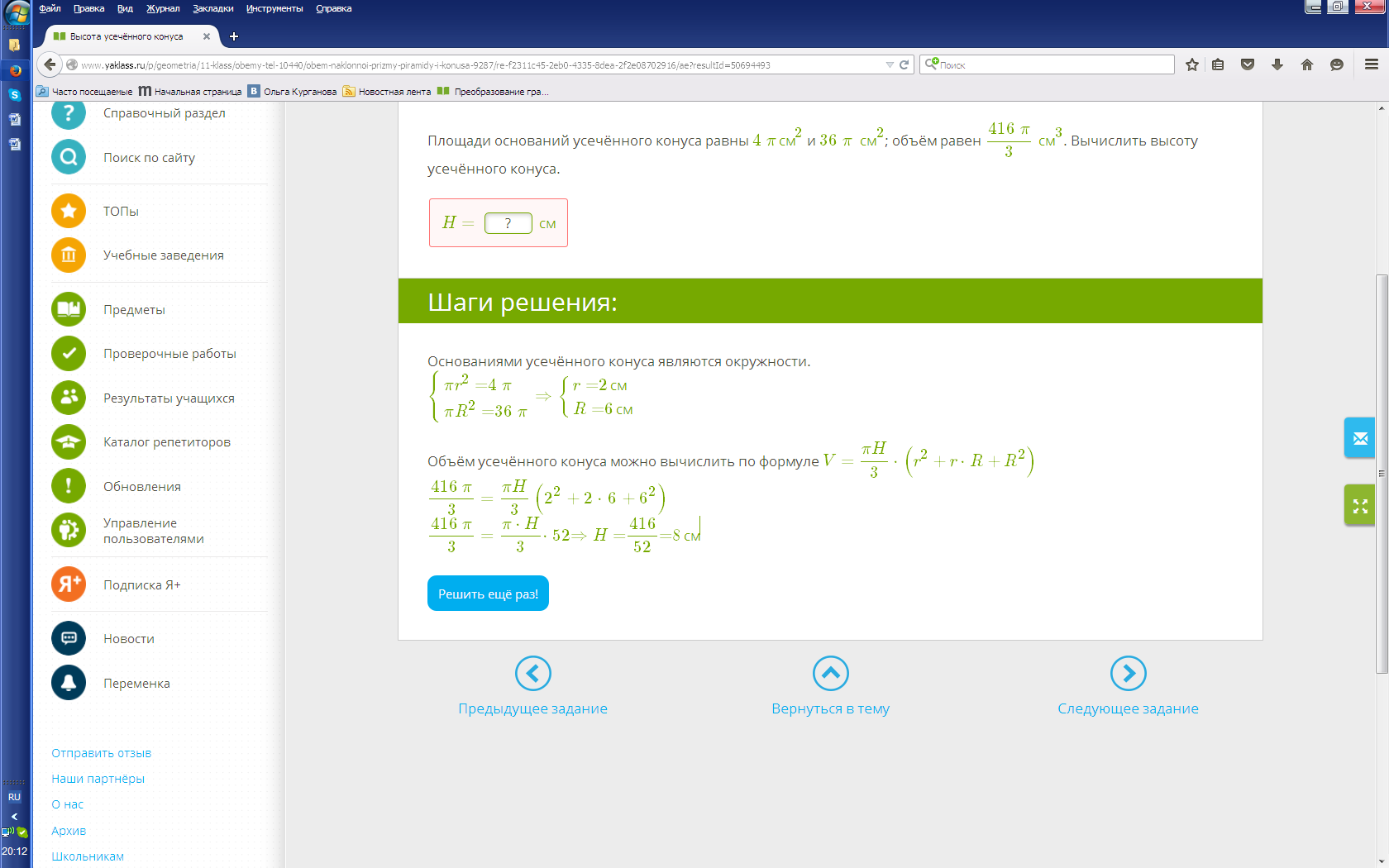 Ответ: Hконуса= 8 см Ответ: Hконуса= 8 см | |
| Решить задание на ЯКласс | №4 Высота усечённого конуса |
Задание № 5 Осевое сечение конуса
| Осевым сечением конуса является равносторонний треугольник, сторона которого равна 12мм. Вычисли объём конуса. | |
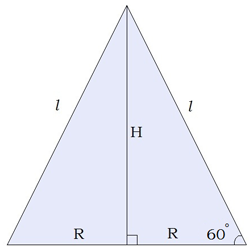 | Дано: а=12мм Найти: Vконуса-? |
Решение: На рисунке — осевое сечение конуса. V=πR 2  R= R= 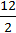 =6мм H=6 =6мм H=6 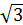 мм, по соотношению в прямоугольном треугольнике, угол в котором равен 30 o . V= мм, по соотношению в прямоугольном треугольнике, угол в котором равен 30 o . V= 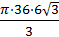 V= V= 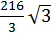 ⋅π мм 3 ⋅π мм 3 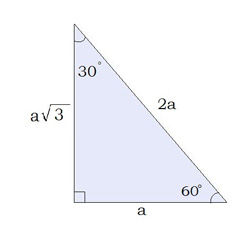 Ответ: V= Ответ: V= 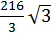 ⋅π мм 3 ⋅π мм 3 | |
| Решить задание на ЯКласс | №5 Осевое сечение конуса |
Содержание отчета
a) Записать дату, Тему занятия и его цель
b) Записать решение заданий в тетрадь.
c) Ответить на контрольные вопросы письменно.
Контрольные вопросы
| Какую часть от объема цилиндра занимает объем конуса, если известно, что высота и основания у них одинаковы?. | |
| Врашением какой фигуры и вокруг какой оси образуется усеченный конус? | |
| Что такое осевое сечение конуса? | |
| Какие фигуры могут иметь правильный треугольник в качестве осевого сечения? | |
| 5. | По какой формуле вычисляется объем пирамиды? |
Дата добавления: 2016-03-15 ; просмотров: 5833 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Найти длина окружности основания конуса
Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники . На рисунке 168 осевым сечением конуса является треугольник ABP ( АР = ВР ). Угол АPВ называют углом при вершине осевого сечения конуса .
Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.
Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP ).
Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).
Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением .

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.
ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60 ° ; б) в 90 ° . Найти площадь сечения.
Решени е. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.
Хорда АВ окружности основания стягивает дугу в 60 ° , значит, △ AOB — правильный и АВ = R .
Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S △ ABP = 



Тогда S △ ABP = 

Ответ: а) 
18.3. Касательная плоскость к конусу
Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.
Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.
Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.
18.4. Изображение конуса
Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).
Для достижения наглядности изображения невидимые линии изображают штрихами.
Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.
18.5. Развёртка и площадь поверхности конуса
Пусть l — длина образующей, R — радиус основания конуса с вершиной Р .
Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a ), то получим развёртку поверхности конуса (рис. 176, б ), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса ; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):
α = 
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.
Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле
S бок = 
где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = 
Таким образом, доказана следующая теорема.
Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼
Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.
S кон = π Rl + π R 2 . (3)
Следствие. Пусть конус образован вращением пря м оугольного треугольника ABC вокруг катета АС (рис. 177). Тогда S бок = π • BC • АВ. Если D — середина отрезка АВ, то AB = 2 AD, поэтому
S бок = 2 π ВС • AD. (4)
Проведём DE ⟂ АB ( E ∈ l = AС ) . Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А ) имеем


Тогда соотношение (4) принимает вид
S бок = (2 π • DE ) • AC, (6)
т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.
Это следствие будет использовано в п. 19.7.
18.6. Свойства параллельных сечений конуса

Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Доказательств о. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α , параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).
Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β , α || β , то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O 1 = α ∩ РО. Обозначим этот круг F 1 .
Рассмотрим гомотетию 
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия 



где k — коэффициент гомотетии 
А поскольку гомотетия является подобием, то круг F 1 , являющийся параллельным сечением конуса, подобен его основанию.
Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO 1 : Р О , где РO 1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
S сечен : S основ = k 2 = 
18.7. Вписанные в конус и описанные около конуса пирамиды
Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.
Для построения изображения правильной пирамиды, вписанной в конус:
— строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;
— соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;
— выделяют видимые и невидимые (штрихами) линии изображаемых фигур.
На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:
— прямоугольный треугольник (см. рис. 179);
🎥 Видео
Длина окружности. Площадь круга - математика 6 классСкачать

Конус. Площадь боковой поверхности конуса.Скачать

КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Длина окружности. 9 класс.Скачать

Цилиндр, конус, шар, 6 классСкачать

Объём цилиндраСкачать

РАДИУС ОСНОВАНИЯ ? Конус / база #506339Скачать

Длина дуги окружности. 9 класс.Скачать

Длина окружности. Практическая часть. 9 класс.Скачать

Площадь сектора и сегмента. 9 класс.Скачать

МЕРЗЛЯК-6. ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА. ПАРАГРАФ-25Скачать

КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

№555. Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конусаСкачать

Длина окружности. Площадь круга, 6 классСкачать

8 класс. ОГЭ. Найти диаметр окружностиСкачать

Длина окружности и площадь кругаСкачать

КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР ИЛИ РАДИУС? Примеры | МАТЕМАТИКА 6 классСкачать














