Через вершину а равнобедренного треугольника авс с основанием ас проведена прямая ад параллельная вс

Геометрия | 5 — 9 классы

Через вершину А равнобедреного ттреугольника АВС с основанием ВС проведена прямая, паралельная стороне ВС.

Вычислите градусную меру угла САВ, если угол АВС = 75 градусов( не использовать то, что сумма углов треугольника равна 180 градусов, только свойства параллельных прямых ).

Рассмотрим треугольник АВС.

Угол АВС = 75 градусов, т.

К. прямые параллельны, = > угол АВС = углу ВАD( т.

К. они внутренние накрест лежащие).

Треугольник равнобедренный, угол АВС = 180 — (75 + 75) = 30 градусов.

Видео:Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать

Известо что сумма углов = 180 градусов найдите градусную меру угла при основании равнобедренного треугольника если его внешний угол при вершине = 124 градуса?

Известо что сумма углов = 180 градусов найдите градусную меру угла при основании равнобедренного треугольника если его внешний угол при вершине = 124 градуса.

Видео:№243. Через вершину С треугольника ABC проведена прямая, параллельная его биссектрисе АА1Скачать

В треугольнике АВС угол В равен 90 градусов?

В треугольнике АВС угол В равен 90 градусов.

Через вершину С проведена прямая, параллельная стороне АВ и образует с АС угол, равный 36 градусам.

Найдите углы А и С.

Видео:№473. Через вершину С треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите,Скачать

В треугольнике АВС угол С равен 90 градусов ?

В треугольнике АВС угол С равен 90 градусов .

Через вершину А проведена прямая АД параллельная стороне СВ Угол ДАВ = 54 градуса .

Найдите углы В и САв .

Видео:№235. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD. Найдите углыСкачать

Треугольник АВС — равнобедренный, АС — основание треугольника?

Треугольник АВС — равнобедренный, АС — основание треугольника.

Угол АВС = 30 градусов.

Через вершину В проведена прямая ЕF, параллельная АС.

Докажите, что углы АВЕ и CBF равны.

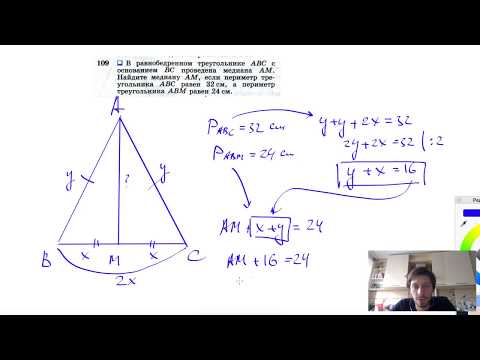
Видео:№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать

Через вершину А треугольника ABC с прямым углом С проведена прямая параллельная BC?

Через вершину А треугольника ABC с прямым углом С проведена прямая параллельная BC.

Вычислете градусную меру угла ABC если угол CAB = 50 градусов.

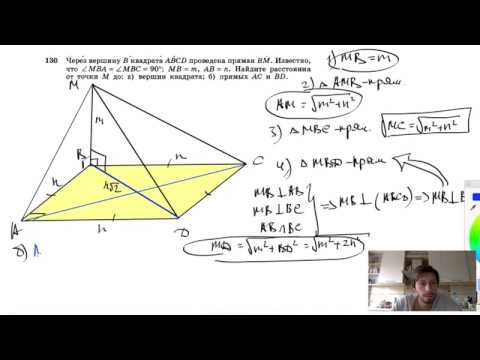
Видео:№130. Через вершину В квадрата ABCD проведена прямая ВМ. Известно, что ∠MBA = ∠MBC=90°, МВ =m, АВСкачать

Через вершину B треугольника ABC проведена Прямая параллельная стороне AC Вычислите градусную меру угла ABC если BAC равен 40 градусов BCA равен 70 градусов?

Через вершину B треугольника ABC проведена Прямая параллельная стороне AC Вычислите градусную меру угла ABC если BAC равен 40 градусов BCA равен 70 градусов.

Видео:№245. Через точку пересечения биссектрис ВВ1 и СС1 треугольника ABC проведена прямая, параллельнаяСкачать

Через вершину В треугольника АВС проведена прямая, пенпендикулярная высоте ВD ?

Через вершину В треугольника АВС проведена прямая, пенпендикулярная высоте ВD .

Вычислите градусные меры углов АВD и DВС, если известно что угол ВАС = 35 градусов, угол ВСА = 70 градусов.

Видео:№145. Через вершину А прямоугольного треугольника ABC с прямым углом С проведена прямая AD,Скачать

В треугольнике авс угол а = 90 градусов, а угол с на 40 градусов больше угла в?

В треугольнике авс угол а = 90 градусов, а угол с на 40 градусов больше угла в.

Чему равна градусная мера угла с?

Видео:№155. Через вершину прямого угла С равнобедренного прямоугольного треугольника ABCСкачать

Через вершину прямого угла С прямоугольного треугольника АВС к его плоскости проведен перпендикуляр СД?

Через вершину прямого угла С прямоугольного треугольника АВС к его плоскости проведен перпендикуляр СД.

Найти длину стороны АВ треугольника АВС, если АД = 20 см, СД = 16 см, угол САВ = 60 градусов.

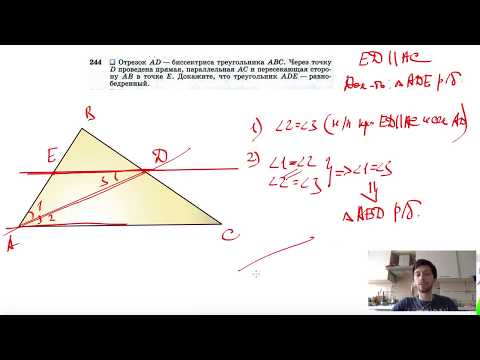
Видео:№244. Отрезок AD — биссектриса треугольника ABC. Через точку D проведена прямая, параллельная АССкачать

Найти градусную меру угла при вершине равнобедренного треугольника, если мера угла при основании равна 30 градусов?

Найти градусную меру угла при вершине равнобедренного треугольника, если мера угла при основании равна 30 градусов.

На странице вопроса Через вершину А равнобедреного ттреугольника АВС с основанием ВС проведена прямая, паралельная стороне ВС? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

1) если диагональ биссектрисса, то параллелограмм является ромбом. Значит все четыре стороны равны, делим 34 / 4 = 8, 5 cм. Значит ВС = 7, 5см. 2) если угол 45, то треугольник будет равнобедренный и его вторая сторона тоже будет 5 см. Из большего..

4 оси имеет прчмоугольник.

Радиус основания цилиндра S1 = πR² = 16π ; R² = 16 ; R = 4 см. Сторона осевого сечения равна диаметру основания цилиндра ; равна 8 см. Площадь осевого сечения равна S2 = 8² = 64 см². Ответ : 64 см².

S поверхности шара = 4πR = 2. 5S = 4 * π *  = 4 * π * 6. 25 = 25π.

Какая фигура имеет четыре стороны одной длинны? (квадрат) перимет какой геометрической фигуры равен — (a + b)•2.

Вот вроде, думаю правильно.

Рассмотрим треугольники rsd и psd pd = rd — дано rs = ps — дано ds — общая сторона треугольники rsd и psd равны, следовательно угол pds = углу rds угол pds + угол rds = 360 — 98 = 262 (град. ) угол rds = 262 : 2 = 131 (град. ).

Ответы и решения на фото.

H = √3a / 2 r = √3a / 6 — радиус вписанной окружности R = √3a / 3 — радиус описанной окружности.

Если mh 3 см, а угол mnh 30°, то mh по свойству прямоугольного треугольника = 1 / 2 mn, значит mn 6 см отсюда mn = pq = 6 см mq = mh + hq = 5 + 3 = 8 см mq = np = 8 см находим углы hnp = 90° по свойству перпендикуляра, значит угол n получается угол m..

Видео:№150. Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскостиСкачать

Задача 16 геометрия на ЕГЭ-2021 по математике

На этой странице — обзор разных типов заданий № 16 ЕГЭ-2021 по математике, то есть задач по геометрии.

Все они имеют нечто общее: во-первых, это стандартный уровень сложности, то есть вполне решаемые задачи. Пункт (а) в них вообще простой.

Во-вторых, в каждой из них применяются свойства четырехугольников, вписанных в окружности.

В первой задаче такая окружность находится почти сразу, причем она – вспомогательная, и ее можно даже не изображать на чертеже. Главное – найти равные вписанные углы, опирающиеся на равные дуги или на одну дугу.

Также здесь использована формула синуса тройного угла. Если вы ее забыли – не беда. Ведь а формулу синуса суммы вы знаете.

1. Дана равнобедренная трапеция ABCD, в которой меньшее основание ВС равно боковой стороне. Точка Е такова, что ВЕ перпендикулярно AD и СЕ перпендикулярно BD.
а) Доказать, что угол АЕВ равен углу BDA.
б) Найти площадь трапеции ABCD, если АВ = 32, косинус угла АDВ равен

– равнобедренный, CM – высота, проведенная к основанию, значит, M – середина BD.

Докажем, что точки A, B, C, D, E лежат на одной окружности.

ABCD – равнобедренная трапеция, ее можно вписать в окружность.

В – медиана и высота, значит, равнобедренный, BE = ED.

Тогда по трем сторонам, четырехугольник BCDE можно вписать в окружность, т.к.

Так как вокруг можно описать только одну окружность и вокруг четырехугольников ABCD и BCDE тоже можно описать окружность, точки A, B, C, D, E лежат на одной окружности, так как опираются на одну и ту же дугу AB (точки E и D лежат по одну сторону от прямой AD).

б) Так как AB = BC = CD, то дуги AB, BC и CD также равны.

Четырехугольник ABDE вписан в окружность, тогда

По формуле синуса тройного угла,

тогда по теореме синусов

Проведем в трапеции ABCD высоту CK, тогда

BH и CK – высоты трапеции, а так как трапеция равнобедренная, то

Во второй задаче мы увидим ту же идею: вспомогательную окружность. Это один из методов, помогающих решать задачи ЕГЭ по геометрии. Есть здесь и другой мощный прием – использование двух пар подобных треугольников. И еще свойство высоты прямоугольного треугольника, проведенной к гипотенузе. Если вы в восьмом и девятом классе учили геометрию – вы должны владеть этими приемами.

2. Дан прямоугольный треугольник АВС с прямым углом С. Из вершины С на гипотенузу опущена высота СН, на АС и ВС соответственно отмечены точки М и N так, что угол MHN – прямой.
а) Докажите, что треугольники МNH и АВС подобны.
б) Найдите СN, если АС = 5, СМ = 2, ВС = 3.

а) Рассмотрим четырехугольник CMHN.

по условию, значит, CMHN можно вписать в окружность; вписанные, опираются на дугу HN.

Запишем соотношение сходственных сторон.

По условию, AM = 3, найдем CH — высоту

по теореме Пифагора,

AH — проекция катета AC на гипотенузу, по свойствам прямоугольного треугольника, отсюда

В следующей задаче мы снова видим окружность и вписанную в нее трапецию. И наверное, вы уже заметили: пункт (а) задач по геометрии на ЕГЭ часто оказывается подсказкой для решения пункта (б). То, что мы доказали в (а), мы используем в пункте (б).

3. Даны 5 точек на окружности: A, B, C, D, E, причем АЕ = ED = CD, ВЕ перпендикулярен АС.
Точка Т – точка пересечения АС и BD.
а) Докажите, что отрезок ЕС делит отрезок ТD пополам.
б) Найдите площадь треугольника АВТ, если BD = 10, АЕ =

Докажем, что M — середина TD.

Если AE = ED = DC, то дуги AE, ED, DC, также равны;

— накрест лежащие, при пересечении AC и DE секущей CE, значит, AEDC — равнобедренная трапеция. значит, BD — диаметр окружности.

(опирается на диаметр), по катету и гипотенузе, тогда DM — биссектриса равнобедренного т.к. — равнобедренный, то DM — медиана M — середина CE, кроме того, DM — высота

В — медиана и высота, значит, — равнобедренный, а так как — накрест лежащие, при параллельных прямых AC и DE и секущей CE, то по боковой стороне и углу при основании, тогда

CDET — ромб, M — точка пересечения его диагоналей, M — середина TD.

Мы нашли, что AE = ED = CD = CT = ET.

BD = 10 — диаметр окружности.

— равнобедренный, AE = ET, — высота и медиана

Тогда BN — медиана и высота — равнобедренный, AB = BT.

Обозначим тогда — опираются на дугу AE,

Из по теореме синусов:

И еще одна трапеция, вписанная в окружность. Теперь вы точно выучите ее свойства наизусть! Также здесь применяется теорема о пересекающихся хордах. Все эти полезные теоремы, свойства и признаки можно найти в нашей универсальной шпаргалке – Справочнике Анны Малковой для подготовки к ЕГЭ по математике. Скачать Справочник бесплатно можно здесь.

4. Трапеция с большим основанием AD и высотой ВН вписана в окружность. Прямая BH пересекает окружность в точке К.

б) Найдите AD, если: радиус окружности равен шести, СК пересекается с AD в точке N и площадь четырехугольника BHNC в 24 раза больше, чем плошать треугольника KHN.

а) Трапеция ABCD вписана в окружность, следовательно, AB = CD (трапеция равнобокая)

Тогда — вписанные, опираются одну и ту же на дугу AK;

следовательно, CK — диаметр окружности, так как вписанный угол, опирающийся на диаметр, прямой; — опирается на диаметр CK, значит,

(опираются на дугу BC), тогда

Обозначим так как HE = BC,

Из подобия треугольников KNH и KCB следует, что тогда

По теореме о пересекающихся хордах,

Представив левую часть уравнения как разность квадратов, получим:

По смыслу задачи тогда и значит

Задача по геометрии на ЕГЭ по математике оценивается в 3 балла. Как видите, в 2021 году эти 3 балла за геометрию можно было получить без особенных трудностей. На нашем Онлайн-курсе подготовки к ЕГЭ мы решаем и такие задачи по геометрии, и более сложные. Если ты сейчас в 10-м или в 11-м классе – попробуй бесплатно Демо-доступ к Онлайн-курсу.

5. (Резервный день) Окружность с центром О, построенная на катете АС прямоугольного треугольника АВС, как на диаметре, пересекает гипотенузу АВ в точках А и D. Касательная, проведенная к этой окружности в точке D, пересекает катет ВС в точке М.

А) Докажите, что ВМ = СМ
Б) Прямая DM пересекает прямую АС в точке Р, прямая ОМ пересекает прямую ВР в точке К.

Найдите ВК : КР, если

а) Так как – радиус окружности, – равнобедренный, так как (касательная перпендикулярна радиусу, проведенному в точку касания), тогда

– угол между касательной и хордой,

Тогда т.е. – высота – прямоугольный, – равнобедренный, отсюда

Найдем BK : KP, если тогда

Значит, (вертикальные), — равнобедренный, тогда так как MK – биссектриса

Видео:№563. Через точку М, взятую на медиане AD треугольника ABC, и вершину В проведена прямая,Скачать

ВПР 2020 по математике 7 класс задание №14 реальное с ответами

ПОДЕЛИТЬСЯ

ВПР 2020 по математике 7 класс задания и ответы с решением для реального задания №14 которое будет на официальной всероссийской проверочной работе в 2020 году.

Ссылка для скачивания реальных заданий №14: скачать задания

Ссылка для скачивания ответов и решения к заданиям: скачать в PDF

Решу ВПР 2020 по математике 7 класс ответы и решения задание №14:

Интересные задания с ответами ВПР 2020 математика 7 класс:

1)В треугольнике ABC проведена биссектриса CE. Найдите величину угла BCE, если ∠BAC = 46° и ∠ABC = 78°.

Ответ: 28

2)В треугольнике ABC проведена биссектриса AL, угол ALC равен 121°, угол ABC равен 101°. Найдите угол ACB. Ответ дайте в градусах.

Ответ: 39

3)В треугольнике два угла равны 36° и 73°. Найдите его третий угол. Ответ дайте в градусах.

Ответ: 71

4)В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах.

Ответ: 49

5)В треугольнике ABC проведена биссектриса AL, угол ALC равен 78°, угол ABC равен 52°. Найдите угол ACB. Ответ дайте в градусах.

Ответ: 76

6)В треугольнике АВС известно, что BAC=64 градусов, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Ответ: 32

7)В равнобедренном треугольнике АВС с основанием ВС проведена медиана АМ. Найдите медиану АМ, если периметр треугольника АВС равен 40 см, а периметр треугольника АВМ равен 32 см.

Ответ: 12

8)В равнобедренном треугольнике АВС с основанием ВС проведена медиана АМ. Найдите медиану АМ, если периметр треугольника АВС равен 56 см, а периметр треугольника АВМ равен 42 см.

Ответ: 14 см

9)Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 78 см, а одна из сторон равна 18 см. Найдите две другие стороны треугольника.

Ответ: 18 см, 30 см, 30 см

10)Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 86 см, а одна из сторон равна 20 см. Найдите две другие стороны треугольника.

Ответ: 20 см, 33 см, 33 см

11)Высоты, проведенные к боковым сторонам АВ и АС остроугольного равнобедренного треугольника АВС, пересекаются в точке М. Найдите углы треугольника, если угол ВМС = 140°.

Ответ: 40 градусов, 70 градусов, 70 градусов.

12)В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.

Ответ: 10 градусов

13)На сторонах угла BAC и на его биссектрисе отложены равные отрезки AB, AC и AD.
Величина угла BDC равна 160°. Определите величину угла BAC.

Ответ: 40 градусов

14)На сторонах угла BAC, равного 20°, и на его биссектрисе отложены равные отрезки AB,
AC и AD. Определите величину угла BDC.

Ответ: 170 градусов

15)Отрезки AB и CD — диаметры окружности с центром O. Найдите периметр треугольника AOD, если известно, что CB = 13 см, AB = 16 см.

Ответ: 29 см

16)Отрезки AB и CD — диаметры окружности с центром O. Найдите периметр треугольника AOD, если известно, что CB = 11 см, AB = 17 см.

Ответ: 28 см

17)В треугольнике ABC стороны AB и BС равны, угол B равен C пересекаются в точке M. Найдите величину угла AMC.

Ответ: 128 градусов

18)В треугольнике ABC стороны AB и BС равны, угол B равен 88 градусов. Биссектрисы углов А и C пересекаются в точке M. Найдите величину угла AMC.

Ответ: 134 градуса

19)В треугольнике ABC стороны AB и BС равны, угол B равен 72 градуса. Биссектрисы углов А и C пересекаются в точке M. Найдите величину угла AMC.

Ответ: 126 градусов

21)На продолжении стороны AB равнобедренного треугольника ABC с основанием AC отметили точку D так, что AD = AC и точка A находится между точками B и D. Найдите величину угла , ADC если угол ABC равен 32 градуса.

22)На продолжении стороны AB равнобедренного треугольника ABC с основанием AC отметили точку D так, что AD = AC и точка A находится между точками B и D. Найдите величину угла , ADC если угол ABC равен 44 градуса.

23)На продолжении стороны AB равнобедренного треугольника ABC с основанием AC отметили точку D так, что AD = AC и точка A находится между точками B и D. Найдите величину угла , ADC если угол ABC равен 28 градусов.

24)На продолжении стороны AB равнобедренного треугольника ABC с основанием AC отметили точку D так, что AD = AC и точка A находится между точками B и D. Найдите величину угла , ADC если угол ABC равен 52 градусов.

25)В равнобедренном треугольнике ABC с основанием AC угол B равен 120°. Высота треугольника, проведённая из вершины, A равна 7. Найдите длину стороны AC.

26)В равнобедренном треугольнике ABC с основанием AC угол B равен 120°. Высота треугольника, проведённая из вершины, A равна 5. Найдите длину стороны AC.

27)В равнобедренном треугольнике ABC с основанием AC угол B равен 120°. Высота треугольника, проведённая из вершины, A равна 9. Найдите длину стороны AC.

28)В равнобедренном треугольнике ABC с основанием AC угол B равен 120°. Высота треугольника, проведённая из вершины, A равна 8. Найдите длину стороны AC.

29)Сторона AB треугольника ABC продолжена за точку B. На продолжении отмечена точка D так, что BC=BD. Найдите величину угла, BCD если угол ACB равен 60°, а угол BAC равен 50 .

30)Сторона AB треугольника ABC продолжена за точку B. На продолжении отмечена точка D так, что BC=BD. Найдите величину угла, BCD если угол ACB равен 30°, а угол BAC равен 40°.

31)Сторона AB треугольника ABC продолжена за точку B. На продолжении отмечена точка D так, что BC=BD. Найдите величину угла, BCD если угол ACB равен 75°, а угол BAC равен 35°.

32)Сторона AB треугольника ABC продолжена за точку B. На продолжении отмечена точка D так, что BC=BD. Найдите величину угла, BCD если угол ACB равен 35°, а угол BAC равен 65°.

33)В прямоугольном треугольнике ABC с прямым углом C проведена высота CD. Найдите величину угла A, если DB = 6, а BC =12.

34)В прямоугольном треугольнике ABC с прямым углом C проведена высота CD. Найдите величину угла A, если DB = 8, а BC =16.

35)В прямоугольном треугольнике ABC с прямым углом C проведена высота CD. Найдите величину угла A, если DB = 3, а BC =6.

36)В прямоугольном треугольнике ABC с прямым углом C проведена высота CD. Найдите величину угла A, если DB = 9, а BC = 18.

37)Сторона AB треугольника ABC продолжена за точку B. На продолжении отмечена точка D так, что BC = BD. Найдите величину угла BCD, если угол ACB равен 60°, а угол BAC равен 50°. Ответ дайте в градусах. Запишите решение и ответ.

38)Сторона AB треугольника ABC продолжена за точку B. На продолжении отмечена точка D так, что BC = BD. Найдите величину угла BCD, если угол ACB равен 35°, а угол BAC равен 65°. Ответ дайте в градусах. Запишите решение и ответ.

📸 Видео

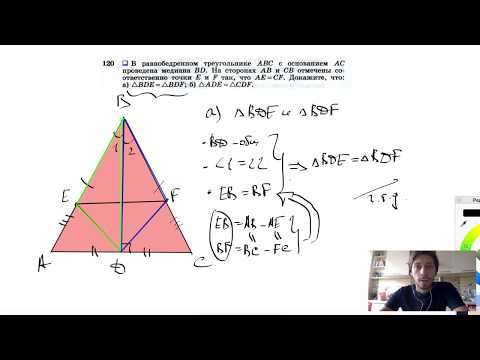
№120. В равнобедренном треугольнике ABC с основанием АС проведена медиана BD. На сторонах АВ и СВСкачать

[ОГЭ] В равнобедренном треугольнике ABC с основанием АС внешний угол при вершине С равен 123°Скачать

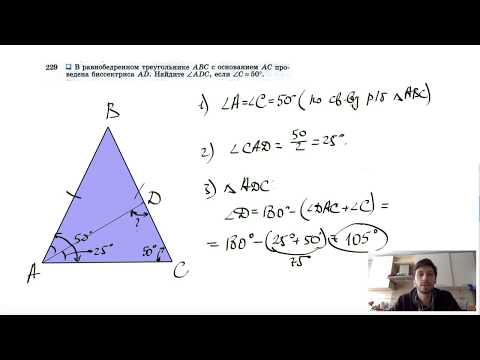
№229. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD.Скачать

№38. Через вершину А ромба ABCD проведена прямая а, параллельная диагонали BD,Скачать

№193. В треугольнике ABC ∠A=40°, ∠B=70°. Через вершину B проведена прямая BD так, что луч ВССкачать

№152. Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. НайдитеСкачать

№149. Отрезок AD перпендикулярен к плоскости равнобедренного треугольника ABC. Известно,Скачать

ОГЭ 2022 Демоверсия. 25 задание | Основание AC равнобедренного треугольника ABC равно 12.....Скачать