Окружность с центром O, вписанная в треугольник ABC, касается стороны BC в точке K. К этой окружности проведена касательная, параллельная биссектрисе AP треугольника и пересекающая стороны AC и BC в точках M и N соответственно.
а) Докажите, что угол MOC равен углу NOK.
б) Найдите периметр треугольника ABC, если отношение площадей трапеции AMNP и треугольника ABC равно 2:7, MN = 2, AM + PN = 6 .
а) Обозначим Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому MO и NO — биссектрисы внешних углов при вершинах M и N треугольника MCN. Значит,
а так как CO — биссектриса угла ACP, получаем, что
Следовательно,
б) Луч MO — биссектриса угла AMN, поэтому Значит, треугольник AOM равнобедренный, AM = AO. Аналогично PN = OP.
Пусть радиус вписанной окружности треугольника ABC равен r, а полупериметр треугольника ABC равен p. Точка O лежит на основании AP трапеции AMNP, поэтому высота трапеции равна r. Тогда
Поскольку получаем, что p = 14, а периметр равен 28.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание
Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать  Через центр О вписанной в треугольник АВС окружности проведена прямая, параллельная стороне ВС и пересекающая стороны АВ и АС соответственно в точках М и N?Геометрия | 10 — 11 классы Через центр О вписанной в треугольник АВС окружности проведена прямая, параллельная стороне ВС и пересекающая стороны АВ и АС соответственно в точках М и N. А) Докажите, что периметр треугольника АMN равен АB + АC. Б) Найдите периметр этого треугольника, если известно, что площадь треугольника АВС равна √15, ВС = 2, а отрезок АО в 4 раза больше радиуса вписанной в треугольник АВС окружности. А) Периметр треугольника AMN равен АМ + AN + MN. Центр вписанной окружности О лежит на пересечении биссектрис внутренних углов треугольника АВС. Следовательно, треугольник ОМВ равнобедренный, так как < ; MOB = < ; OBC (как накрест лежащие при параллельных прямых MN и ВС и секущей ОВ), а < ; MBO = < ; OBC (так как ОВ — биссектриса угла В треугольника АВС). Точно так же в треугольнике NOC имеем ON = NC. MN = MO + ON или MN = MB + NC. AB = AM + MB, AC = AN + NC. Тогда периметр треугольника AMN равен АМ + AN + NO + OM = АМ + AN + NC + MB = АВ + АС, что и требовалось доказать. Б) Из прямоугольного треугольника АОР (радиус в точку касания перпендикулярен касательной) имеем : АР = √(AO² — OP²) = √(16r² — r²) = r√15. Тогда по свойству : «Расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны, равно d = (a + b — c) / 2 = p — c», где с — сторона, лежащая против угла С, имеем : АВ + АС — ВС = 2r√15 (1). С другой стороны по формуле площади треугольника имеем : Sabc = p * r, где р — полупериметр треугольника АВС. Отсюда r = S / p = 2√15 / (AB + AC + BC). Подставляем (2) в (1) : АВ + АС — ВС = 2 * (2√15 / (AB + AC + BC)) * √15. АВ + АС — 2 = 2 * (2√15 / (AB + AC + 2)) * √15. Или (АВ + АС — 2 ) * (AB + AC + 2) = 4 * 15. Или (АВ + АС)² — 4 = 4 * 15, отсюда (АВ + АС) = √(4(1 + 15)) = 8. Но выше мы доказали, что АВ + АС — это периметр треугольника AMN. Видео:Геометрия Точка O центр окружности вписанной в треугольник ABC BC = a AC = b угол AOB = 120 НайдитеСкачать  Из вершины прямого угла С треугольника АВС проведена высота СР?Из вершины прямого угла С треугольника АВС проведена высота СР. Радиус окружности, вписанной в треугольник ВСР, равен 60, тангенс угла ВАС равен 4 / 3 (четыре третьих). Найдите радиус окружности, вписанной в треугольник АВС. Видео:Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать  Из вершины прямого угла С треугольника АВС проведена высота СР?Из вершины прямого угла С треугольника АВС проведена высота СР. Радиус окружности вписанной в треугольник ВСР, равен 8, тангенс угла ВАС равен 3 / 4. Найдите радиус вписанной окружности треугольника АВС. Видео:№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать  Помогите пожалуйста?Из вершины прямого угла С треугольника АВС проведена высота СР. Радиус окружности, вписанной в треугольник ВСР, равен 60, тангенс угла ВАС равен 4 / 3. Найдите радиус окружности, вписанной в треугольник АВС. Видео:№473. Через вершину С треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите,Скачать  В треугольнике АВС стороны равны 3?В треугольнике АВС стороны равны 3. Найдите радиус окружности, вписанной в треугольник. Видео:Геометрия В треугольнике ABC известны длины сторон AB = 18, AC = 36, точка O — центр окружностиСкачать  Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК параллельно АС, ВМ : АМ = 1 : 4?Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК параллельно АС, ВМ : АМ = 1 : 4. Найдите периметр треугольника ВМК, если известно что периметр треугольника АВС равен 25 см. Видео:✓ Простое решение красивой геометрии | Планиметрия | Физтех-2021. Математика | Борис ТрушинСкачать  В прямоугольном треугольнике АВС угол В равен 90, МN средняя линия MN / / АВ?В прямоугольном треугольнике АВС угол В равен 90, МN средняя линия MN / / АВ. Докажите, что радиус окружности вписанный в треугольник АВС, в 2 раза больше радиуса окружности, вписанный в треугольник МNC. Видео:№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать 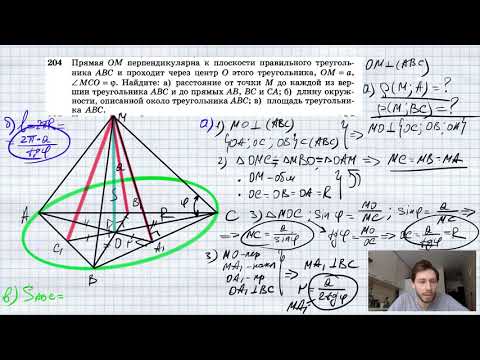 Из вершины прямого угла с треугольника АВС проведена высота СР?Из вершины прямого угла с треугольника АВС проведена высота СР. Радиус окружности, вписанной в треугольник вср, равен 8, тангенс угла ВАС равен 4 3. Найдите радиус вписанной окружности треугольника АВС. Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать  Равносторонний треугольник АВС вписан в окружность радиуса 10см?Равносторонний треугольник АВС вписан в окружность радиуса 10см. Н сторону треугольника. Видео:№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать  Помогите плииз 1)из вершины прямого угла С треугольника АВС проведена высота СР?Помогите плииз 1)из вершины прямого угла С треугольника АВС проведена высота СР. Радиус окружности, вписанной в треугольник ВСР, равен 8, тангенс угла ВАС равен 3 / 4. Найдите радиус вписанной окружности треугольника АВС 2)из вершины прямого угла С треугольника АВС проведена высота СР. Радиус окружности, вписанной в треугольник АСР равен 12 см, тангенс угла АВС равен 2, 4. Найдите радиус вписанной окружности треугольника АВС. Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать  Окружность радиуса 2, вписанная в треугольник АВС, касается средней линии треугольника, параллельной стороне ВС?Окружность радиуса 2, вписанная в треугольник АВС, касается средней линии треугольника, параллельной стороне ВС. Периметр треугольника АВС равен 24. Найти стороны треугольника. Вы перешли к вопросу Через центр О вписанной в треугольник АВС окружности проведена прямая, параллельная стороне ВС и пересекающая стороны АВ и АС соответственно в точках М и N?. Он относится к категории Геометрия, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей. Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Через центр о окружности вписанной в треугольник авс проведена прямая mn параллельная abБАЗА ЗАДАНИЙ Задание № 16. Планиметрия с доказательством. 1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D. 2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно. 3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD. 4. В треугольнике ABC точки A 1 , B 1 , C 1 — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°. 5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно. 6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P. 7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L. 8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N. 9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D. 10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны. 11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно. 12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB. 13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый. 14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C 1 , B 1 соответственно. 15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD. 16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота. 17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M. 18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно. 19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно. б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60. 20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD. 21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K. 22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L 23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части. 24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P. 25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K. 26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности. 27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O. 28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17. 🔍 ВидеоОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать  Задание 3 ЕГЭ по математике. Урок 41Скачать  ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать  2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать  Стереометрия 10 класс. Часть 1 | МатематикаСкачать  №702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать  Окружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать  Задача 16 из проф ЕГЭ по математике основная волна, резервный день. Запад. Вариант 1Скачать  |










