Через точки делящие сторону треугольника на три равные части проведены прямые параллельные другой

Геометрия | 5 — 9 классы

Через точки M и N, делящие сторону AB треугольника ABC на три равные части, проведены прямые, параллельные стороне BC.

Найдите площадь части треугольника, заключённой между этими прямыми, если площадь треугольника ABC равна 1.

Обозначим точки пересечения прямых с стороной AC через K и L.

AK = KL = LC по теореме Фалеса.

AN = 2 / 3 от AB а AL 2 / 3 от AC.

Треугольник ABC подобен ANL подобен AMK.

Так как прямые параллелны и соответсвенные углы равно.

Коэффициент подобия для треугольников ANL и ABC равен 2 / 3 : 1 = 2 / 3

Площади этих треугольников относятся друг другу как квадрат коэфициента подобия тоесть 4 / 9.

S1 — площадь ANL а S2 площадь ABC.

Так как площадь ABC известно и оно ранво 1 то площадь S1 = 4 / 9.

Таким же образом найдем площадь S3 треугольника AMK.

Smkln = S1 — S3 = 3 / 9.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Через середину основания ac равнобедренного треугольника abc проведены прямые параллельные его боковым сторонам?

Через середину основания ac равнобедренного треугольника abc проведены прямые параллельные его боковым сторонам.

Докажите что отрезки этих прямых заключённые внутри треугольника равны.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Две прямые, параллельные стороне ab треугольника abc, делят сторону AC в отношении 2 : 3 : 2?

Две прямые, параллельные стороне ab треугольника abc, делят сторону AC в отношении 2 : 3 : 2.

Найдите площади полученных частей треугольника, если площадь данного треугольника равна 98см2.

Видео:Найдите третью сторону треугольникаСкачать

Через внутреннюю точку треугольника проведены прямые параллельно всем сторонам данного треугольника?

Через внутреннюю точку треугольника проведены прямые параллельно всем сторонам данного треугольника.

Площади образовавшихся треугольников равны 25, 16, 4.

Найдите площадь данного треугольника.

Видео:Бестселлер Все правила по геометрии за 7 классСкачать

Прямая DE параллельна AC треугольника ABC, отсекает от него треугольник DBE, стороны которого в четыре раза меньше сторон данного треугольника?

Прямая DE параллельна AC треугольника ABC, отсекает от него треугольник DBE, стороны которого в четыре раза меньше сторон данного треугольника.

Найдите площадь ABC, если площадь трапеции равна 30.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

В треугольнике ABC проведена медиана BM, на стороне AB взята точка K так, что AK = 1 / 3AB?

В треугольнике ABC проведена медиана BM, на стороне AB взята точка K так, что AK = 1 / 3AB.

Площадь треугольника AMK равна 5.

Найдите площадь треугольника ABC.

Видео:Геометрия 7 класса в одной задаче. Геометрия 7 класс кратко | МатематикаСкачать

Задание 1 Стороны треугольника ABC пересечены прямой MN параллельной AC?

Задание 1 Стороны треугольника ABC пересечены прямой MN параллельной AC.

Периметры треугольника ABC и треугольника MBN относятся как 3 : 1.

Площаль ABC равна 144.

Чему равна площадь треугольника MBN ?

Задание 2 В треугольнике ABC медианы BD, AE CF.

O — точка пересечения медиан.

Площадь треугольника AOD равна 2, 8.

Найдите площадь треугольника BFC.

Задание 3 Периметр треугольника составляет 11 / 13 частей периметра подобного ему треугольника.

Найдите сторону большего треугольника, если соответствующая ей сторона меньше на 1.

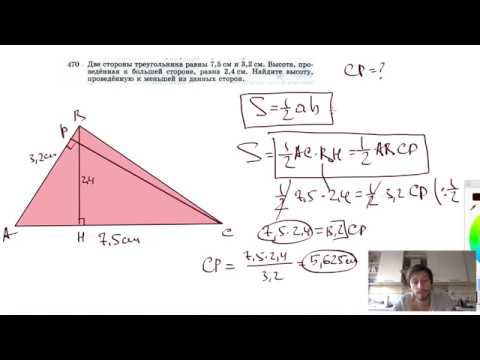
Видео:№470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведенная кСкачать

ПОМОГИТЕ СРОЧНО ?

Через вершину D трапеции ABCD проведена прямая , параллельная боковой стороне AB.

На этой прямой взята точка K.

Найдите площадь трапеции ABCD , если площадь треугольника ABK равна Q , а площадь треугольника ABC = S.

Видео:Треугольники. Практическая часть - решение задачи. 7 класс.Скачать

Средняя линия DE треугольника ABC, параллельна стороне AB?

Средняя линия DE треугольника ABC, параллельна стороне AB.

Площадь треугольника CDE равна 14.

Найдите площадь треугольника ABC.

Видео:Задача про стороны треугольника. Геометрия 7 класс.Скачать

Одна из сторон треугольника разделена на три равные части , и через точки деления проведены прямые, параллельные другой стороне?

Одна из сторон треугольника разделена на три равные части , и через точки деления проведены прямые, параллельные другой стороне.

Найдите отношения площади данного треугольника к площадям треугольников , отсеченных построенными прямыми.

Если можно с рисунком.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Средняя линия DE треугольника ABC параллельная стороне AB?

Средняя линия DE треугольника ABC параллельная стороне AB.

Площадь треугольника CDE равна 12.

Найдите площадь треугольника ABC.

На этой странице находится вопрос Через точки M и N, делящие сторону AB треугольника ABC на три равные части, проведены прямые, параллельные стороне BC?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Ответ : (x + 4)² + y² = 16Объяснение : Уравнение окружности с центром в точке О(х₀ ; у₀) и радиусом R имеет вид : (x — x₀)² + (y — y₀)² = R²По условию R = 4, значит точка А имеет координаты ( — 4 ; 0). Подставляем : (x — ( — 4))² + (y — 0)² = 4²(x +..

Только вместо 6 подставь свое значение 14 тр. AВD = тр. ADМ (по двум сторонам BD = DM, AD — общая, и глу между ними) АМ = АВ = 6см АС = 2АВ = 2 * 6 = 12 Ответ : 12.

Первый случай — расположение по разные стороны от прямой. Воспользуемся координатным методом. Координата нужна только одна, х, вторая, y, не важна и мы её просто не будем указывать S1(18), И1( — 8) Координата точки Щ1 найдётся как среднее арифметич..

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Точки M и N делят сторону BC треугольника ABC на три равные части (M лежит ближе к B). Прямая, параллельная стороне АС, пересекает

Видео:КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Ваш ответ

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

решение вопроса

Видео:Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,701
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Через точки делящие сторону треугольника на три равные части проведены прямые параллельные другой

Видео:✓ Все сюжеты по планиметрии из ЕГЭ за 50 минут | ЕГЭ. Задание 16. Профильный уровень | Борис ТрушинСкачать

Разделы

Видео:Задание 24 Отношение площадей подобных треугольниковСкачать

Дополнительно

Задача по математике — 6803

Найдите высоту прямоугольного треугольника, опущенную на гипотенузу, если известно, что основание этой высоты делит гипотенузу на отрезки, равные 1 и 4.

Задача по математике — 6804

Высота равнобедренного треугольника, опущенная на боковую сторону, разбивает её на отрезки, равные 2 и 1, считая от вершины треугольника. Найдите основание треугольника.

Задача по математике — 6805

Стороны треугольника равны 10, 17 и 21. Найдите высоту треугольника, проведённую из вершины наибольшего угла.

Задача по математике — 6806

Точки $L$ и $N$ — середины оснований соответственно $BC$ и $AD$ трапеции $ABCD$, а точки $K$ и $M$ — середины диагоналей $AC$ и $BD$ соответственно. Известно, что $KM=LN$.
а) Докажите, что сумма углов при одном из оснований трапеции равна $90^$.
б) Найдите высоту трапеции, если известно, что площадь четырёхугольника $KLMN$ равна 12, а разность оснований трапеции равна 10.

Задача по математике — 6807

Диагональ $BD$ трапеции $ABCD$ ($ADparallel BC$) разбивает её на два равнобедренных треугольника с основаниями $AD$ и $DC$.
а) Докажите, что луч $AC$ — биссектриса угла $BAD$.
б) Найдите $CD$, если известны диагонали трапеции: $BD=5$ и $AC=8$.

Задача по математике — 6808

В окружность вписаны две трапеции. Основания и боковые стороны одной из них соответственно параллельны основаниям и боковым сторонам другой.
а) Докажите, что диагонали одной трапеции равны диагоналям другой.
б) Найдите отношение площадей этих трапеций, если известно, что боковая сторона одной из них равна радиусу окружности, а боковая сторона другой в два раза меньше.

Задача по математике — 6809

Диагональ $AC$ прямоугольника $ABCD$ с центром $O$ образует со стороной $AB$ угол $30^$. Точка $E$ лежит вне прямоугольника, причём $angle BEC=120^$.
а) Докажите, что $angle CBE=angle COE$.
б) Прямая $OE$ пересекает сторону $AD$ прямоугольника в точке $K$. Найдите $EK$, если известно, что $BE=40$ и $CE=24$.

Задача по математике — 6810

Дан треугольник $ABC$ со сторонами $AB=4$, $BC=6$ и $AC=8$.
а) Докажите, что прямая, проходящая через точку пересечения медиан и центр вписанной окружности, параллельна стороне $BC$.
б) Найдите длину биссектрисы треугольника $ABC$, проведённой из вершины $A$.

Задача по математике — 6811

В параллелограмме $ABCD$ точка $M$ — середина стороны $AD$, $P$ — точка пересечения отрезка $BM$ с диагональю $AC$.
а) Докажите, что прямая $DP$ проходит через середину стороны $AB$.
б) Биссектриса угла $BAC$ пересекает отрезок $BM$ в точке $Q$. Найдите отношение $PM:BQ$, если известно, что $AB:AC=1:3$.

Задача по математике — 6812

Биссектриса $AD$ треугольника $ABC$ делит его медиану $BM$ пополам.
а) Докажите, что площадь треугольника $ACD$ вдвое больше площади треугольника $ABD$.
б) В каком отношении медиана $BM$ делит биссектрису $AD$?

Задача по математике — 6813

На основаниях $AD$ и $BC$ трапеции $ABCD$ отмечены точки $M$ и $N$ соответственно, а на боковых сторонах $AB$ и $CD$ — точки $K$ и $L$ соответственно. При этом $DM:AM=CN:BN=BK:AK=CL:LD=1:2$.
а) Докажите, что четырёхугольник $KMLN$ — трапеция.
б) Известно, что $AD=3BC$. В каком отношении диагональ $BD$ трапеции $ABCD$ делит боковые стороны трапеции $KMLN$?

Задача по математике — 6814

На сторонах $AD$ и $BC$ параллелограмма $ABCD$ взяты соответственно точки $M$ и $N$, причём $M$ — середина $AD$, а $BN:NC=1:3$.
а) Докажите, что прямые $AN$ и $AC$ делят отрезок $BM$ на три равные части.
б) Найдите площадь четырёхугольника, образованного пересечениями прямых $AN$, $AC$, $BD$ и $BC$, если площадь параллелограмма $ABCD$ равна 40.

Задача по математике — 6815

Вневписанная окружность равнобедренного треугольника касается его боковой стороны.
а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание.
б) Известно, что радиус этой окружности в пять раз больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?

Задача по математике — 6816

Точки $B_$ и $C_$ лежат на сторонах соответственно $AC$ и $AB$ треугольника $ABC$, причём $AB_:B_C=AC_:C_B$. Прямые $BB_$ и $CC_$ пересекаются в точке $O$.
а) Докажите, что прямая $AO$ делит пополам сторону $BC$.
б) Найдите отношение площади четырёхугольника $AB_OC_$ к площади треугольника $ABC$, если известно, что $AB_:B_C=AC_:C_B=1:2$.

Задача по математике — 6817

На диагонали $BD$ параллелограмма $ABCD$ отмечены точки $P$ и $Q$, причём $BP=PQ=QD$.
а) Докажите, что прямые $AP$ и $AQ$ проходят через середины $M$ и $N$ сторон $BC$ и $CD$ соответственно.
б) Найдите отношение площади пятиугольника $CMPQN$ к площади параллелограмма $ABCD$.

🎦 Видео

ЕГЭ Задание 16 Отношение площадейСкачать

Задание 26 Подобные треугольникиСкачать

ВСЕ правила и формулы ПЛАНИМЕТРИИСкачать