Черчение эллипс как проекция окружности построение овала (5 видео)

Чертежик

Содержание

Метки
Построение овала
ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ ОКРУЖНОСТЕЙ
Способы построения эллипса
💥 Видео

Метки

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Построение овала

Рассмотрим построение овала двумя методами: окружности и параллелограмма.

Воспользуемся методом окружности.

1.) Начинаем чертить с построения осей.

2.) Чертим окружность

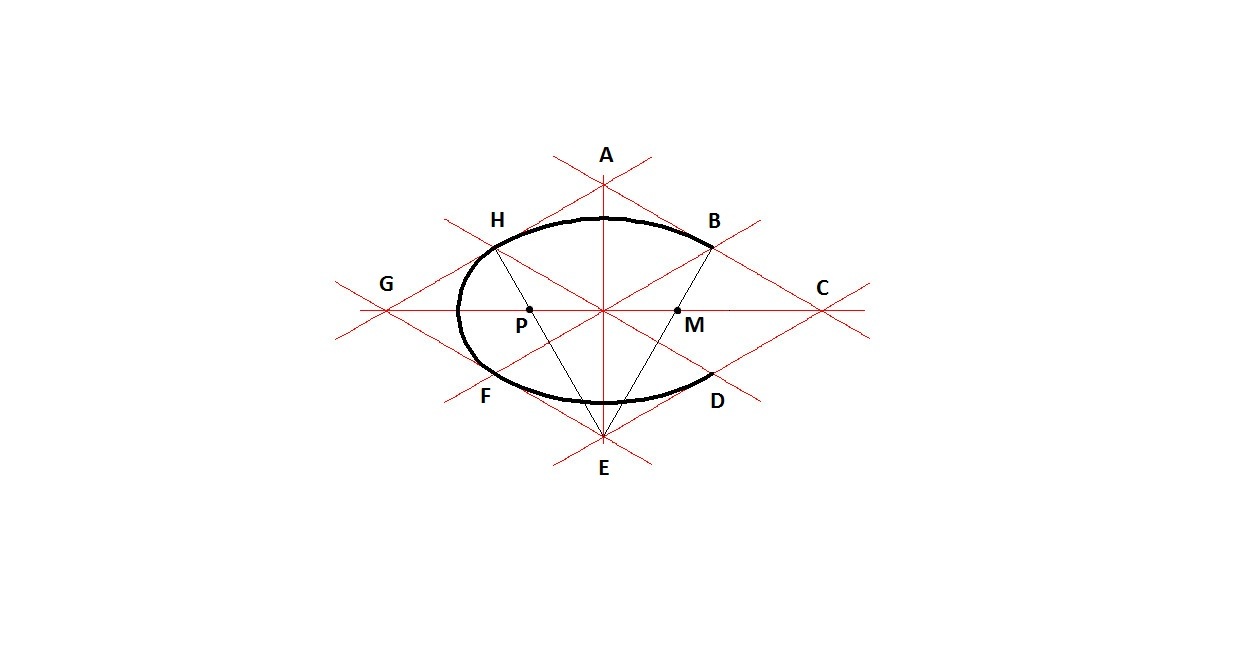
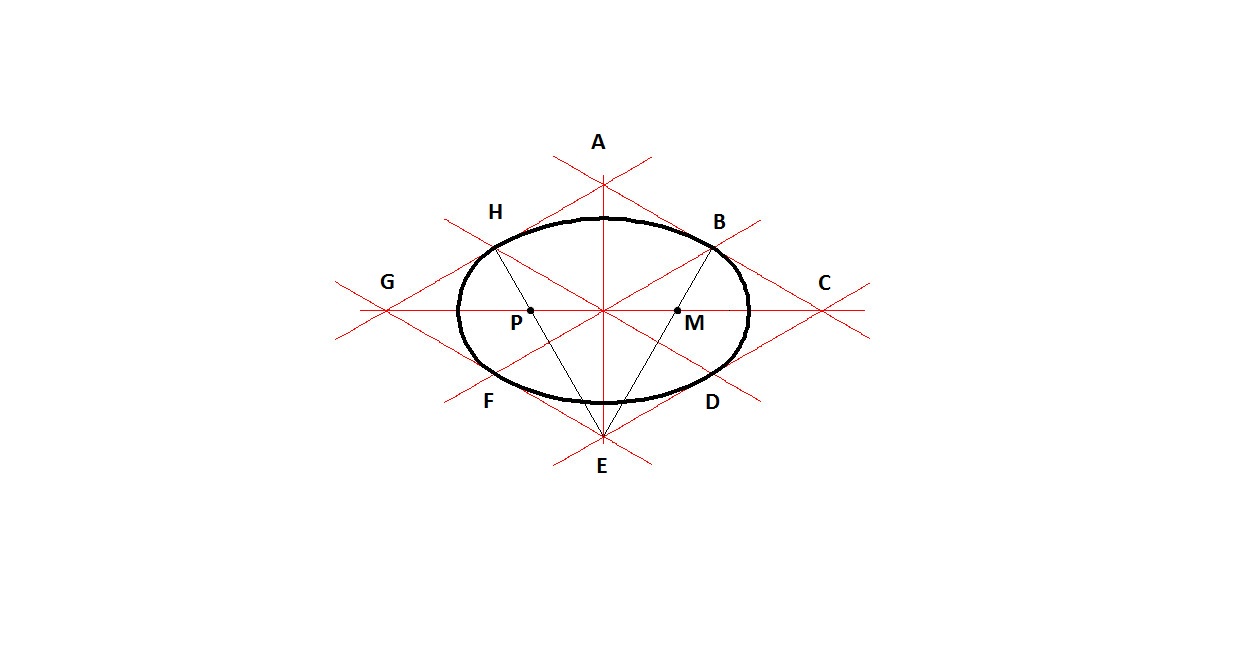
3.) Чертим дуги ЕА и BD радиусом ЕС

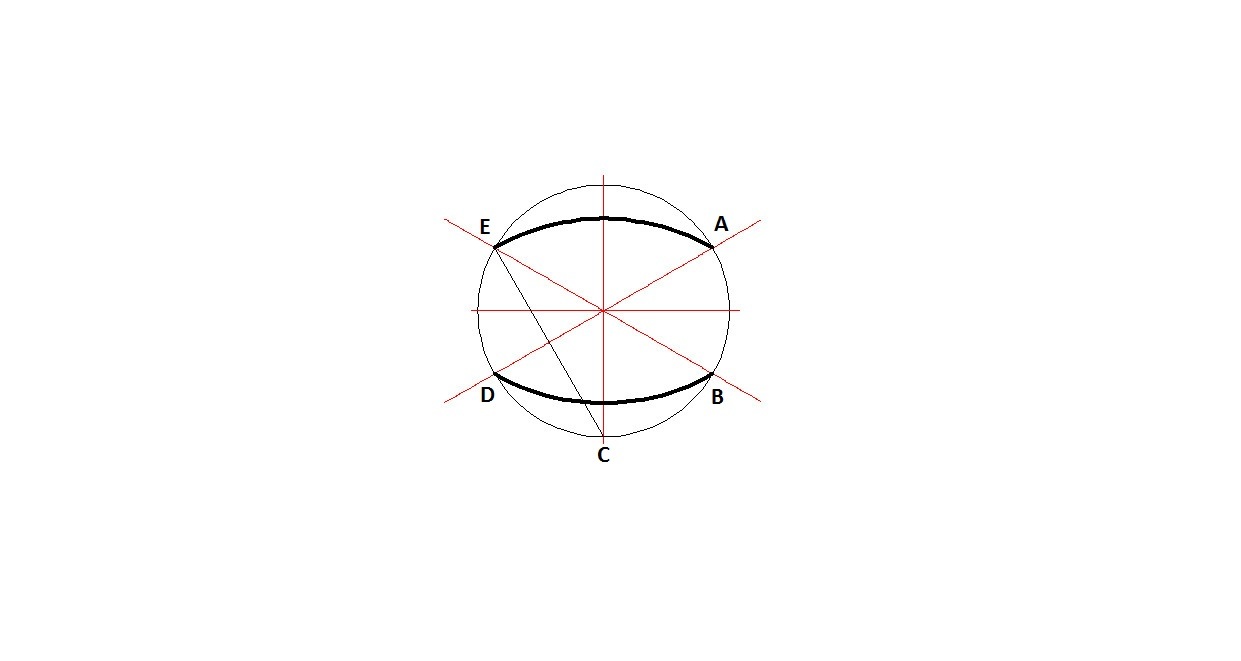
4.) Чертим дуги ED и AB радиусом FB

Применим метод параллелограмма.

1.) Начинаем с построения осевых линий

2.) Чертим линии параллельные осевым линиям. Где d — диаметр окружности.

3.) Строим дуги HB и DF радиусом HE4.) Продолжаем с черчения дуги BD радиуса MB и дуги FH радиусом PH

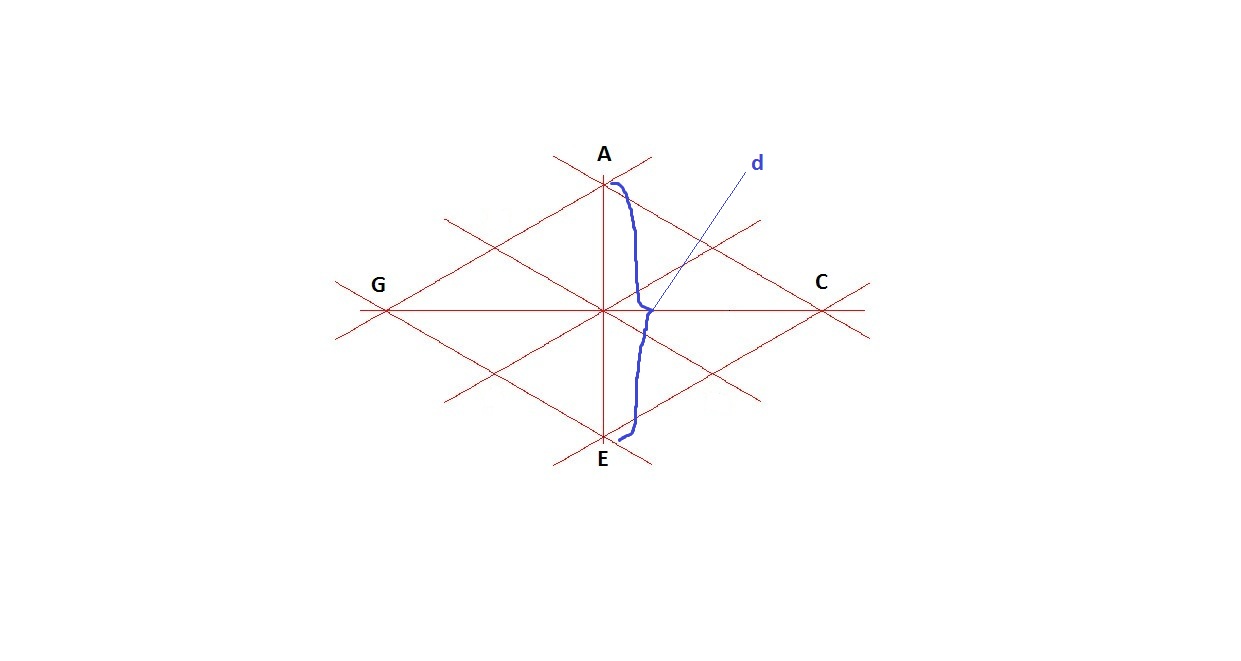
Применение построения овала на чертежах вы можете посмотреть здесь

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ ОКРУЖНОСТЕЙ

Окружности в изометрической проекции изображаются эллипсами (рис. 2.55). Их строят с помощью специальных инструментов — лекал. Это процесс трудоемкий. Поэтому в практике выполнения чертежей эллипсы заменяют овалами. Овал — кривая, состоящая из четырех дут окружности.

Рассмотрим построение овала в горизонтальной плоскости, представляющего собой изометрическую проекцию окружности. Строить овал целесообразно путем вписывания его в ромб, который является изометрической проекцией квадрата, описанного вокруг окружности (рис. 2.56, а).

1. Строим оси хиу изометрической проекции (рис. 2.56, б).
2. Строим аксонометрическое изображение квадрата, описанного вокруг окружности. Обратите внимание, что сторона квадрата равна диаметру окружности. Для этого от точки О на осях х и у откладывают отрезки, равные радиусу изображаемой окружности.
3. Через точки, полученные на оси х — 4 и 2, проводим прямые, параллельные оси у, а через точки на оси у — прямые, параллельные оси х. Получим ромб. Отметим точки А и В и проведем большую диагональ ромба, которая пройдет через точку О (рис. 2.56, в).

4. Из вершин тупых углов ромба точек А и В проводим дуги. Их радиус равен расстоянию от вершин тупого угла до точек 4, 3 или /, 2 соответственно (рис. 2.56, г).

Чтобы найти центры меньших дуг овала, через точки А и 4, А и 3 проводят прямые, которые, пересекаясь с большей диагональю ромба, дадут нам точки, которые будут центрами Oj и 0₂ малых дуг овала. Их радиус равен /. Дугами радиуса /?, проводят малые дуги овала (рис. 2.56, д, е).

Аналогичным способом строят овалы, лежащие во фронтальной и профильной плоскостях. Для овала во фронтальной плоскости построение ведут по осям хи^,ав профильной плоскости — по осям zny (рис. 2.57).

На рис. 2.58 показано построение овала без вписывания его в ромб.

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Способы построения эллипса

Для изложения дальнейшей части курса необходимо вспомнить способы построения эллипсов.

На рис. 20 и 21 показаны способы построения эллипса по его главным осям, а на рис. 22, 23, 23′ даны способы построения эллипса по двум сопряженным диаметрам а₀Ь₀ и c₀d₀.

Напомним, что диаметр а₀Ь₀ (см. рис. 22), сопряженный данному диаметру c₀d₀, делит пополам хорды, параллельные диаметру c₀d₀, и наоборот.

Для построения эллипса по заданным его главным осям на рис. 20 описаны две вспомогательные окружности.

Диаметр большой окружности принят равным большой оси эллипса, а диаметр малой окружности равен малой оси эллипса.

Разделив большую окружность на произвольное число частей, намечаем на ней точки 1, 2, 3, 4, . . Соединяя затем точки 1, 2, 3, 4, . . с центром О, получаем на малой окружности точки 1_1з 2_Ь 3_1з 4_1з . .

Закончив это предварительное построение, проводим из точек 1, 2, 3, 4, . вертикальные линии, а из точек 1₁₅ 2_1з 3_1з 4_1з . горизонтальные линии до пересечения с проведенными уже из точек 1, 2, 3, 4, . вертикальными линиями.

Полученные в местах пересечения точки 1₀, 2₀, 3₀, 4₀, . соединяем по лекалу и этим самым намечаем очертание эллипса, отвечающего заданным осям а₀Ъ₀ и c₀d₀ (см. рис. 20). Нетрудно видеть, что проделанное построение сводится по существу к построению эллипса как фигуры, родственной двум построенным окружностям. Действительно, если принять большую ось эллипса а₀Ь₀ за ось родства, а точки с₀ и с, расположенные на продолжении малой оси, — за родственные точки при совмещенных центрах родственной окружности и эллипса в точке О, то можно рассматривать точки эллипса 1₀, 2₀, 3₀, 4₀, . как точки, родственные точкам окружности 1, 2, 3, 4, . .

В самом деле, если обозначить большую полуось а₀О эллипса через R, а малую полуось с₀О — через г, то

Рис. 23‘

Нетрудно усмотреть, что точно в таком же отношении точки 1₀, 2₀, 3₀, 4₀, . делят хорды, параллельные вертикальной оси сО. Например, для точки 1₀ из подобия треугольников HjIq и 1 On (см. рис. 20) можно написать такое же соотношение:

На рис. 21 показан другой способ построения эллипса по его главным осям.

В данном случае эллипс строится при помощи ключа пропорциональности (рис. 21, а). Для построения ключа откладываем по горизонтальной линии отрезок от произвольной величины и в точке о на перпендикуляре ос» к линии от откладываем размеры большой и малой полуосей эллипса. Намеченные в результате этого построения точки q и с» соединяем с точкой т. Делим далее отрезок от на несколько частей точками 1, 2, 3 и, проводя через точки деления 1, 2, 3 вертикальные линии 1 — 1″, 2 — 2″, 3 — 3″, намечаем на линиях тс₁ и тс» отрезки, пропорциональные отрезкам линии от.

После построения ключа пропорциональности переходим к определению точек 1₀, 2₀, 3₀, принадлежащих эллипсу.

Для этой цели описываем радиусом о₀а₀ окружность (рис. 21, б) и, перенося на нее точки 1″, 2″, 3″. намечаем точки 1′, 2′, 3‘. . После этого точки эллипса 1₀, 2₀, 3₀, . будут найдены в местах пересечения вертикальных линий 1′ — 1₀, 2′ — 2₀, 3′ — 3₀, . с горизонтальными линиями 1_х — 1₀, 2_г — 2₀, 3₁ — 3₀, . .

Убедиться в том, что фигура а₀1о2₀3₀с₀3₀. есть эллипс, можно следующим способом.

Принимаем ось а₀Ь₀ за ось абсцисс X, а ось о₀с’ —за ось ординат Y.

Тогда можно будет написать для какой-либо точки эллипса, например для точки 3₀, и соответствующей точки (3′), отношение ординат в таком виде:

Подставляя эти значения в уравнение (34), получаем откуда

Следовательно, для данного ключа отношение ординат точек окружности 7′, 2′, 3′. к ординатам точек кривой 1₀, 2₀, 3₀. есть величина постоянная. Уравнение окружности может быть выражено через координаты X и Y принадлежащих ей точек, в частности через координаты точки 3′, следующим образом:

Подставляя сюда значение уу, выраженное через ординату у_3о в (36), получим:

или после преобразования будем иметь

т. е. уравнение эллипса, имеющего полуоси: что и требовалось доказать.

На рис. 22 показано построение эллипса по его двум сопряженным диаметрам а₀Ь₀ и c₀d₀, заданным по величине и по направлению. Нетрудно видеть, что в данном случае эллипс также рассматривается как фигура, родственная окружности, описанной на его диаметре а₀Ь₀. Направление родства определяется путем соединения точки окружности с с концом с₀ сопряженного диаметра c₀d₀. Диаметр c₀d₀ в данном случае будет родственным диаметру окружности cd, а хорды 1₀ — 8₀, 2₀ — 7₀, 3₀ — 6₀, . родственны соответственно одноименным хордам окружности. Точки эллипса 1₀, 2₀, с₀, 3₀, 4₀, . оказываются в этом случае родственными точкам 1, 2, 3, с, 3, 4, . окружности. Число точек на окружности может быть взято произвольно.

На рис. 23 и 23′ показан другой способ построения эллипса по двум его сопряженным диаметрам. Этот способ основан на свойствах аффинного преобразования отрезков сторон квадрата, описанного около окружности, в аффинно соответствующие им отрезки сторон паралле- лограма, построенного на сопряженных диаметрах эллипса, родственного данной окружности.

Осью родства на рис. 23 является линия a-Jo^ а направление родства параллельно линии ОО₀.

Построение ведем в такой последовательности (см. рис. 23′):

1) на сопряженных диаметрах а₀Ь₀ и c₀d₀ строим параллелограм ааjbjb;
2) делим сторону параллелограма аЪ на равные части точками 1, 2, 3 и 4 и на столько же равных частей делим диаметр c₀d₀ точками 11 > 2j, и
3) соединяем точки 1 и 2 с точкой а₀, а точки 3 и 4 — с точкой Ь₀;
4) из точек а₀ и Ь₀ проводим штрихпунктирные линии через точки 1_Ь 2₁ до пересечения с пунктирными линиями Ь₀4, Ь₀3, а₀1, а₀2;
5) соединяем плавной чертой полученные точки пересечения 1₀, 2₀, 3₀, 4₀, . и этим намечаем очертание искомого эллипса.

Построение главных осей эллипса

При построении косоугольной аксонометрической проекции окружности приходится определять величину и направление главных осей эллипса по заданным его сопряженным диаметрам (по величине и по направлению, см. табл. 37 в ч. 2).

В этом случае рекомендуется использовать следующий способ (рис. 24).

Радиусом OY₀ описываем четверть окружности и намечаем точку У₀ Соединяем точку Yq с точкой Х₀, являющейся концом сопряженного диаметра XqXq. Линию У₀‘Х₀ продолжаем в обе стороны за точки У₀‘ иХ₀.

Делим пополам отрезок YqX₀ и из полученной точки с, как из центра, проводим полуокружность через центр эллипса О.

Точки тип пересечения этой полуокружности с линией YqX₀ лежат на главных осях эллипса. При этом отрезок тХ₀ = а равен по величине большой полуоси эллипса От₀, а отрезок пХ₀ = b равен малой полуоси эллипса Ол₀.

Вычерчивание эллипса при помощи кругов кривизны

Для приближенного построения эллипса можно применить прием, показанный на рис. 25. На главных осях т₀т₀ и п₀п₀ строим прямоугольник.

Соединив точку п₀ с точками т₀ и т₀, опускаем на линии п₀ — т₀ перпендикуляры из точек а и Ь. Эти перпендикуляры в пересечении с главными осями намечают точки с, с_г и с₂, являющиеся центрами, из которых можно циркулем описать значительную часть очертания эллипса. Участки, отмеченные пунктиром, должны быть соединены при этом по лекалу или на глаз от руки.