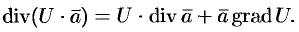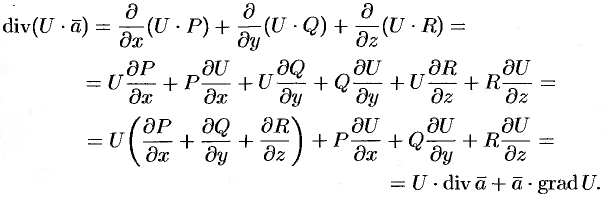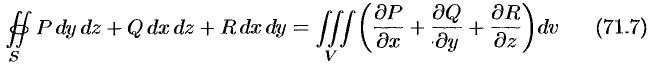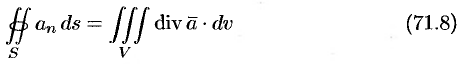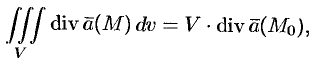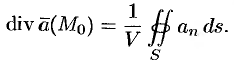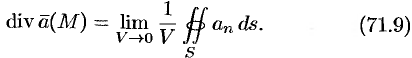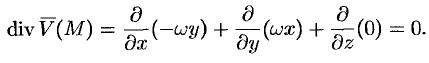Дивергенция поля. Формула Остроградского-Гаусса
Важной характеристикой векторного поля (71.1) является так называемая дивергенция, характеризующая распределение и интенсивность источников и стоков поля.
Дивергенцией (или расходимостью) векторного поля
в точке 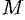
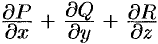
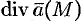
Отметим некоторые свойства дивергенции.
- Если
— постоянный вектор, то
.
, где
.
, т. e. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
- Если
— скалярная функция,
— вектор, то
Эти свойства легко проверить, используя формулу (71.6). Докажем, например, справедливость свойства 4.
Так как 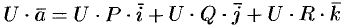
Используя понятия потока и дивергенции векторного поля, запишем известную в анализе (см. (58.9)) формулу Остроградского Гаусса
в так называемой векторной форме.
Рассматривая область 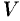
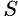
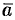
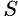
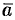
(в котором она чаще всего и встречается).
Формула Остроградского-Гаусса означает, что поток векторного поля через замкнутую поверхность 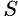
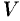
Используя формулу (71.8), можно дать другое определение дивергенции векторного поля 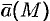
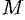
По теореме о среднем для тройного интеграла (см. п. 54.1) имеем:
где 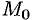
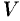
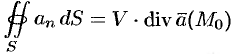
Пусть поверхность 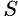
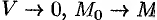
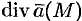
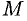
Дивергенцией векторного поля в точке 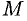
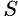
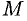
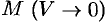
Определение (71.9) дивергенции эквивалентно (можно показать) определению (71.6).
Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном поле.
Исходя из физического смысла потока (обычно условно считают; что 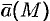
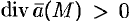
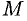
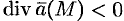
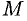
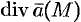
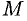
Понятно, что если в объеме 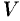
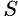
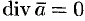
Векторное поле, в каждой точке которого дивергенция поля равна нулю, т. е. 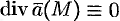
Пример №71.4.
Найти дивергенцию поля линейных скоростей 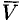
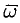
Решение:
Примем ось вращения жидкости за ось 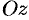
Поле 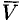
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:ДивергенцияСкачать

Векторное поле. Дивергенция. Вихрь
Допустим в каждой точке некоторой области пространства задан вектор А , тогда считается, что в этой области пространства задано векторное поле. Например, в трубе определено поле скоростей частиц текущей жидкости. Векторное поле наглядно изображается векторными линиями. Векторной линией называется такая линия, в каждой точке которой вектор, соответствующий этой точке, направлен по касательной к векторной линии.
Рассмотрим некоторые основные понятия, связанные с векторным полем. При изучении этих понятий будем приписывать векторам поля некоторый физический смысл: будем считать, что векторное поле есть поле скоростей текущей жидкости.
Выделим в векторном поле поверхность S (замкнутую или незамкнутую). Вычислим объем жидкости, протекающей через эту поверхность за единицу времени. Для этого разобьем поверхность на п малых элементов Л5’,,Л52 ^. Л5я . Объем жидкости, протекающей через элемент ASi за единицу времени, будет, равен A1cos
Если число элементов п увеличить до бесконечности, уменьшая при этом размеры каждой элементарной площадки до нуля, то объем жидкости будет:
Пределы подобного вида называют интегралами по поверхности S и обозначаются следующим образом:
Этот интеграл называется потоком вектора А через поверхность векторного поля S. Поток вектора может быть записан следующим образом:
где п — единичный вектор нормали к поверхности; Ах, Лу, Аг, А„ — проекции вектора А, соответственно на оси координат и нормаль к поверхности; пх, пу, т — углы этой нормали с осями координат.
Возьмем какую-нибудь точку поля М> в некотором малом объеме К, поверхность которого обозначим S; вычислим поток вектора через эту поверхность S. Рассмотрим предел, к которому стремится отношение этого потока к объему V при условии, что объем V стягивается в точку М.
Предел этот называется дивергенцией, или расходимостью вектора:
Если вычислить этот предел, то окажется, что
Дивергенцию от вектора А можно рассматривать как скалярное произведение двух векторов: А и символического вектора V (набла):
С учетом одного из свойств скалярного произведения основных единичных векторов:
получим скалярное произведение двух векторов:
По этой формуле вычисляем скалярное произведение:
Операции второго порядка даются формулами:
Пусть заданы скалярная Ф=Ф(г, t) и векторная F = F(r,t) функции кривой, описываемой радиус вектором г = /•(/) или х = x(t) , у = y(t) ,
2 = z(t) и параметром /. Их полные производные вдоль кривой г = г(/) по отношению к параметру t равны соответственно:
Пусть поле вектора А есть поле скоростей несжимаемой жидкости, причем в начале координат имеется источник жидкости е в этом случае
дивергенция вектора А, вычисленная для начала координат, будет равна +е. Если в начале координат имеется не источник жидкости, а сток, то дивергенция в этом случае будет равна
е . Вообще дивергенция поля скоростей текущей жидкости в данной точке есть относительное изменение плотности элемента жидкости, отнесенное к единице времени.
Основная теорема, связанная с понятием дивергенции, — теорема Остроградского — заключается в следующем:
Пусть для некоторого объема V пространства, ограниченного поверхностью S задано поле некоторого вектора А . Обозначим через S поверхность, ограничивающую этот объем. Формула Остроградского устанавливает зависимость между тройным интегралом, взятым по объему V, и двойным интегралом, взятым по поверхности S:
Интеграл от дивергенции вектора через объем V равен интегралу потока вектора через поверхность S, ограничивающую этот объем.
Рассмотрим в векторном поле какую-либо кривую L. Линейным интегралом вектора А вдоль кривой L называется интеграл, взятый по кривой
Если кривая L замкнута, то линейный интеграл называется циркуляцией вектора (rot А) по кривой L. Понятие линейного интеграла аналогично понятию работы. Если точка перемещается по кривой L под действием силы вектора А, проекции которой на оси координат равны AXiAy> Az, то линейный интеграл (2.3) представляет собой работу, совершенную этой силой.
Этот интеграл зависит не только от конечной и начальной точек интегрирования, но также и от кривой, по которой производится интегрирование. Интегралы (2.3), взятые по разным кривым, соединяющим данные фиксированные точки, — различны.
Однако, если подынтегральное выражение в линейном интеграле есть полный дифференциал d(p некоторой функции или вихрь вектора А) и является величиной векторной.
С учетом векторного произведения основных единичных векторов: 
Применяя это произведение, легко проверить, что вектор-вихрь можно рассматривать как векторное произведение вектора-набла на вектор

Очевидно, что вихрь потенциального вектора равен нулю:
Если вектор А есть вектор скорости текущей жидкости, то вектор
rot А для некоторой точки является удвоенной угловой скоростью вращения бесконечно малого объема, окружающего эту точку, в предположении, что этот объем в данный момент времени затвердел.
Основная теорема, связанная с понятием вихря, есть теорема Стокса. Пусть S — некоторая поверхность, ограниченная контуром L и целиком расположена в векторном поле. Теорема Стокса устанавливает связь между циркуляцией вектора по кривой L и интегралом, взятым по поверхности S.
Циркуляция вектора А по замкнутому контуру равна потоку вектора гоЫ через поверхность, ограниченную этим контуром:
Дивергенция от градиента скалярной величины есть величина скалярная:
где V 2 — оператор Лапласа; /=1,2,3 — соответственно координаты х,у и г.
Оператор скалярного произведения двух векторов (а • v): 

где индексы 1,2,3 соответствуют координатам x,y,z соответственно.
Можно показать, что
где (grad/i) т и (ул) г в AV -транспонированная диада.
Видео:Демидович №4429: дивергенция произведения функций от радиус-вектораСкачать

Элементы теории поля и векторного анализа (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 |


Пример 1.2. Найти 
Аналогично, 

Последнее соотношение можно использовать для получения напряженности поля для сферически-симметричных потенциалов, то есть для потенциалов, поверхности уровня которых представляют собой сферы.
1.3 Оператор C
Определение Оператором называется правило, по которому одной функции ставится в соответствие другая функция.
Предположим, мы имеем две функции f и φ.Соотношение f = Tφ, где T — оператор, устанавливает соответствие между ними, Например, если 

Заметим, соотношение (1.3) не зависит от того, какое скалярное поле мы дифференцируем. Эту формулу можно записать компактно, если ввести дифференциальный векторный оператор C (читается «набла»).

В многих случаях с оператором ∇ можно обращаться как с обычным вектором. ∇ = 

Примечание Вообще говоря, не любые три оператора образуют векторный оператор. (Также как не любые три числа образуют вектор.) Компоненты векторных операторов, как и компоненты обычных векторов, при преобразовании системы координат должны преобразовываться определенным образом. Можно провести и более простые рассуждения, показывающие, что ∇ — векторный оператор. В предыдущем разделе мы показали, что grad f = ∇ f — вектор, направленный по нормали к поверхности уровня. Поскольку, формально соотношение (1.6) выглядит как действие оператора на скалярную функцию и в результате получается вектор, то поэтому ∇ — векторный оператор.
Пример 1.3. Вычислить вектор 
Последовательно проводим действия:
1. Находим частные производные от функции



2. Каждую из полученных производных умножаем на соответствующий единичный вектор, полученные векторы складываем и результат умножаем на функцию 

3. Вычисляем полученный вектор в точке (1,2,0):

1.4 Действия с оператором ∇. Дивергенция вектора. Ротор вектора.
Рассмотрим векторное поле A(x, y,z) = Из двух векторов ∇ и A по обычным правилам векторной алгебры можно образовать скалярное произведение:

Эта скалярная величина называется дивергенцией вектора A и обозначается как divA:

Из векторов ∇ и A можно образовать и векторное произведение. Используя обычные правила векторной алгебры, получим:

Эта векторная величина называется ротором вектора A и обозначается как rotA:

Примечание Определения (1.1) и (1.13) даны в прямоугольной системе координат. К независящим от выбора системы координат определениям дивергенции и ротора функции, а также к их смыслу мы вернемся позже.
В различных применениях векторного анализа часто возникает необходимость в вычислении div(Af) и rot(Af), где A — векторное поле, f-скалярное. Получим соответствующие формулы, используя (1.8), (1.10) и (1.12):


Пример 1.4. Вычислить divr, где r = – радиус вектор:
Пример 1.5. Вычислить rotr, где, по-прежнему, r = – радиус вектор:
Пример 1.6. Вычислить div(rφ(r)),где r = – радиус вектор, r — его длина, φ(r) – произвольная дифференцируемая функция от r.
Используя формулу (1.14) и решения примеров 1.2 и 1.4, получаем
Пример 1.7. Вычислить rot(rφ(r)),где r, r и φ(r) определены в примере 1.6.
Используя формулу (1.15) и решения примеров 1.2 и 1.5, получаем:
1.5 Некоторые формулы векторного анализа
До сих пор мы рассматривали действие оператора ∇ на скалярные и векторные поля и их произведения. Сейчас мы получим некоторые часто встречающиеся в приложениях соотношения, в которых оператор ∇ встречается дважды.
1.5.1 Вычисление rot gradf
Пустьf(x, y,z) – некоторое скалярное поле. Тогда, используя формулы (1.3) и (1.10) получим:

Этот же результат можно получить проще, используя, оператор ∇.
rot gradf = [∇,(∇f] = [∇,∇]f = 0, так как векторное произведение вектора самого на себя равно нулю.
1.5.2 Вычисление div rot A
Используя соотношения (1.8) –(1.11) и правила для вычисления смешанного произведения векторов, получаем:

так как в определителе две одинаковых строки.
1.5.2 Вычисление div gradf. Оператор Лапласа.
Используя соотношения (1.6) –(1.9) и правила для вычисления скалярного произведения векторов, получаем:

Оператор 

Оператор Лапласа может действовать и на векторное поле A(x, y,z). По определению:
ΔA = i ΔAx+ j ΔAy+ k ΔAz (1.20)
1.5.3 Вычисление rot rotA.
Для вычисления используем известную формулу для двойного векторного произведения:
где A, B, C– три произвольных вектора.
rot rotA = [∇,[∇A]] = ∇(∇,A)-( ∇,∇)A = grad divA — ΔA (1.21)
Разумеется, эту же формулу мы получим, используя (1.12) и расписывая выражение rot rotA по компонентам.
Последняя строка в этом выражении, сумма слагаемых в которой равна нулю, добавлена для удобства вычислений. Группируя слагаемые со знаком “+”и со знаком “-“ и принимая во внимание равенство смешанных производных, получим:

Примечание Последние вычисления показывают преимущества использования оператора ∇ при рассмотрении различных векторных соотношений, содержащих дифференцирование.
📸 Видео
Демидович №4427: дивергенция радиус-вектораСкачать

ДивергенцияСкачать

Определить дивергенцию следующих векторных полей... Волькенштейн 9.1 а и бСкачать

Александр Чирцов: ротор, дивергенция и градиентСкачать

Радиус векторСкачать

Дивергенция векторного поляСкачать

#8 Ротор/Дивергенция/ГрадиентСкачать

Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Дивергенция векторного поля. Гидродинамическая аналогия. Теорема Остроградского.Скачать

Демидович №4438: дивергенция векторного произведенияСкачать

Радиус-векторыСкачать

Демидович №4430: дивергенция произведения функции и градиентаСкачать

41. Основные понятия теории векторных полейСкачать

Демидович №4441б: поток радиус-вектора через замкнутую поверхностьСкачать

2.4. Радиус-вектор и вектор перемещенияСкачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

РоторСкачать


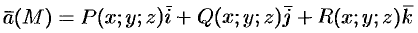
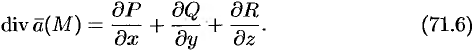
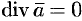 .
.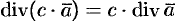 , где
, где 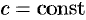 .
.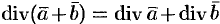 , т. e. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
, т. e. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых. — скалярная функция,
— скалярная функция,