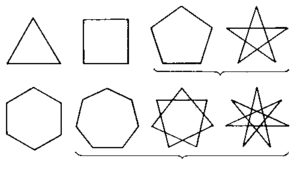
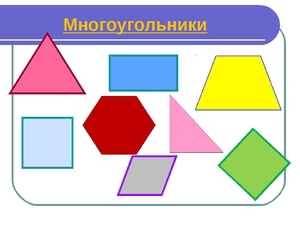
Чем отличаются четырехугольник и многоугольник (5 видео)

Что такое многоугольник в математике — виды, свойства и примеры фигур с названиями

Геометрическую фигуру, ограниченную со всех сторон ломанной линией, называют многоугольником. В математике такое понятие применимо для множества объектов, образованных из трёх и более отрезков. Фигуры, относящиеся к этому классу, могут иметь как произвольную форму, так и строгую. Например, семиугольник, квадрат. Но при этом их всех объединяют одинаковые свойства и ряд правил.

Содержание

Общие сведения
Простейшие четырёхугольники
Треугольный многоугольник
Теорема об углах
Четырехугольники и многоугольники
Четырехугольники и многоугольники.
Свойства параллелограмма:
Геометрическая фигура многоугольник
Основные понятия
Виды фигур
Треугольник
Четырехугольник
Видео
Видео

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Общие сведения

Основной линией, с помощью которой образовывается многоугольная фигура, называется ломанная. Это несколько последовательно соединённых между собой отрезков. Если при этом они друг друга не пересекают, кривую считают простой. В ином случае говорят про ломанную с самопересечением. Каждый отрезок, входящий в кривую, называют звеном. Точки, ограничивающие его — вершинами.

Нарисовать ломанную можно по-разному. Главное, соблюдать правило последовательного соединения точек отрезков. Если при этом получится рисунок, на котором первая вершина начального отрезка совпадёт с последней вершиной (ломанная замкнётся), такая кривая называется замкнутой. Но чаще используется другое название — многоугольник. Другими словами, это фигура, образованная соединёнными между собой прямыми, состоящая из отрезков без самопересечения.

Любого вида многоугольник состоит из следующих частей:

Две прямые линии, соединяющиеся у вершины, образуют угол. Он получается при пересечении лучей, проходящих по сторонам фигуры. Именно от количества углов, получаемых при построении, тот или иной геометрический объект может иметь своё уникальное название. Например, тело с тремя углами — треугольник, четырьмя — четырёхугольник, пятью — пятиугольник.

Понятия применимы не только к плоскости, но и к пространству. Так, во втором случае с помощью ломанной образовывается пространственный многоугольник. Его особенность в том, что вершины тела не лежат в одной плоскости и как минимум фигура должна иметь их по меньшей мере 4. Многоугольник с n вершинами называется n—угольником.

Каждая фигура со множеством углов имеет особые линии. Это такие отрезки, построение которых помогает охарактеризовать тело. Одной из них является диагональ. Это элемент, который получается при соединении отрезком двух несоседних вершин. Таких замкнутых прямых в многоугольнике может быть много. При этом из одной вершины можно строить несколько диагоналей.

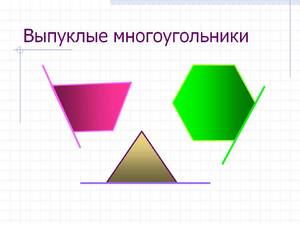
А также все многоугольники разделяют на 2 типа — выпуклые и невыпуклые. Тело хотя бы с одним углом, смотрящим внутрь, относится ко второму типу, а тот, чьи углы направлены наружу — к первому. В школьном курсе геометрии изучают только второй вид, расположенный на плоскости. Более сложными видами многоугольников занимается стереометрия и планиметрия.

Видео:Геометрия 8 класс (Урок№1 - Многоугольники. Четырёхугольник.)Скачать

Простейшие четырёхугольники

Любой многоугольник, который состоит из четырёх углов, называют четырёхугольным. Он относится к простейшим геометрическим телам. Если о нём ничего не известно, его считают произвольным, то есть фигурой, у которой нет особенных углов или сторон. В другом случае четырёхугольники имеют собственные названия.

Наиболее часто приходится сталкиваться со следующими видами:

прямоугольник — четырёхугольник, у которого все углы прямые, то есть равняются 90 0 ;
ромб — фигура с четырьмя сторонами одинаковой длины;
квадрат — многоугольник, удовлетворяющий одновременно условиям ромба и прямоугольника.

Для всех этих видов характерно, что каждая из фигур имеет 2 пересекающиеся диагонали. Причём точка их соприкосновения делит отрезок на 2 равные части. Кроме этого, для прямоугольника и квадрата длина одной диагонали равна другой. Если у четырёхугольного прямоугольника обозначить стороны a и b, противоположные им грани также будут a и b.

Каждый отрезок, образующий многоугольник, имеет свою длину. При их сложении получается периметр фигуры. Для его обозначения используют заглавную латинскую букву P. Например, если есть многоугольник, образованный сторонами AB, BC, CA, его периметр будет равняться: Pabc = AB + BC + CA. Можно обратить внимание, что количество углов соответствует числу сторон, складываемых для нахождения P. Это важный параметр, позволяющий оценить размер фигуры.

Из-за особенностей прямоугольника формулу для расчёта периметра можно переписать так: P = 2*(a + b). В то же время площадь такой фигуры находится путём простого перемножения примыкающих сторон: S = a*b. Параметры квадрата можно вычислить, зная длину только одной стороны. Всё дело в том, что длины отрезков, из которых он состоит, равны друг другу, поэтому для квадрата периметр находится как P = 4*a, а площадь: S = a*a = a 2 .

Прямая четырёхугольная фигура является частным случаем ромба. А значит, что все формулы, указанные для квадрата, справедливы и при применении к нему. Следует отметить, что площадь ромба может быть найдена и как половина произведения его диагоналей.

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Треугольный многоугольник

Такую фигуру называют треугольником. Она состоит из трёх углов и такого же числа сторон. Их, принято обозначать маленькими буквами a, b, c или подписывать двумя заглавными по названиям вершин, которые являются началом и концом отрезка. Например, треугольник ABC содержит стороны: AB = a, BC = b, AC = c.

В зависимости от особенностей, фигура может называться:

разносторонней — многоугольник, у которого все 3 стороны не равны;
равнобедренной — длины любых двух граней совпадают;
равносторонней (правильной) — все стороны фигуры одинаковые.

Но несмотря на классификацию, все перечисленные виды обладают общими свойствами. Считается, что угол любого плоского треугольника образуется при пересечении двух лучей, содержащих его стороны, то есть если говорят об ∠A, то подразумевают, что был лучи AB и АС, при построении которых он и образовался. Таким образом, он заключается не между сторонами, а лучами.

Как и для любого другого многоугольника, у треугольника есть периметр и площадь. Следуя из определения первого, для фигуры с вершинами ABC он будет равен сумме длин всех сторон: P = a + b + c. У треугольников существуют так называемые замечательные линии: медиана, биссектриса, высота.

Эти 3 параметра определяют свойства треугольной фигуры. С их помощью можно находить, площадь, стороны, значения углов. Определение медианы звучит так: это прямая, проведённая из угла к противолежащей стороне таким образом, что разделяет её пополам. Под биссектрисой же понимают отрезок, разделяющий угол на 2 равные части. Высотой называют перпендикуляр, опущенный на противоположную сторону из вершины.

Треугольник, который выглядит, как прямой угол, называют прямоугольным. То есть построив в любом многоугольнике с тремя углами высоту, можно получить две фигуры, обе из которых точно будут прямоугольными. Боковые грани, перпендикулярные друг другу, называют катетами, а оставшуюся сторону — гипотенузой. По сути, тело представляет собой разделённый диагональю квадрат. Отсюда площадь многоугольника будет равняться произведению катетов, делённых на 2: S = a*b/2. А также следует отметить, что у равнобедренного треугольника медиана, высота и биссектриса совпадают.

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Теорема об углах

Многоугольники бывают выпуклые и вогнутые. Чтобы узнать, какой из них приходится рассматривать в том или ином случае, можно сделать следующее. Через каждую сторону провести прямую. Если по отношению к любой из них фигура будет лежать в одной полуплоскости относительно неё, многоугольник считается выпуклым, в ином случае — вогнутым.

Для первого типа существуют важные соотношения. Пусть имеется произвольный многоугольник. Интерес представляет сумма всех его углов. Посчитать её можно следующим образом. Нужно взять любую вершину и соединить её со всеми оставшимися прямой линией. В результате получится несколько треугольников. Затем нужно посчитать их количество. Например, в шестиугольнике их будет 4, восьмиугольнике — 6. Это число легко находится, так как существует правило, согласно которому в любой n-угольной фигуре можно построить n-2 треугольника.

В каждом треугольнике сумма углов равняется 180 градусов. Отсюда следует, что искомая сумма будет равняться 180 0 * (n — 2). Например, для восьмиугольного она равняется 180 * (8 — 2) = 1080 0 . Для многоугольника можно вести понятие внешнего угла.

К любой вершине можно построить 2 таких смежных угла. Если взять каждый из них, то их сумма будет равняться: a1 + a2 +…+ an = 360 0 . Доказать это можно так. Угол a1 равняется (180 — ∠A1), a2 = (180 — ∠A2) и так далее. Таких слагаемых будет n штук. Тогда можно записать, 180 * n — 180 * (n — 2) = 180 * 2 = 360. Таким образом, сумма всех внешних углов равняется 360 0 .

Лучше всего понять сказанное можно, рассмотрев пример, рассчитанный на учащихся средней школы. Пусть есть правильный шестиугольник. Нужно определить его угол. У такой фигуры все стороны, а значит и углы равны. Для начала следует определить их сумму. Она будет равняться 180 * (4−2) = 180 0 * 4 = 720 0 . Но так как это шестиугольник, результат необходимо поделить на 6. Таким образом, искомый угол правильной фигуры будет равняться 120 градусам.

Видео:ЧЕТЫРЕХУГОЛЬНИК и его элементы. §1 геометрия 8 классСкачать

Четырехугольники и многоугольники

Видео:Математика 1 класс Урок 9 Четырёхугольник Обозначение четырёхугольникаСкачать

Четырехугольники и многоугольники.

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны.

Свойства параллелограмма:

1. В параллелограмме противоположные стороны и углы попарно равны.

2. Диагональ делит параллелограмм на два равных треугольника.

3. Диагонали точкой пересечения делятся пополам.

4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

5. Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.

6. В параллелограмме биссектрисы углов, прилежащих к одной стороне (соседних углов), пересекаются под углом в $90°$.

Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними. $S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
Площадь параллелограмма равна произведению основания на высоту. $S=h_a·a$, где $a$ — сторона параллелограмма, $h_a$ — высота, проведенная к стороне $a$.

Прямоугольник — это параллелограмм, у которого все углы прямые.

Все свойства параллелограмма (Так как прямоугольник – это тот же параллелограмм, только особенный, поэтому у него присутствуют все свойства параллелограмма).
Диагонали прямоугольника равны.

Площадь прямоугольника равна половине произведения смежных (соседних) сторон.

$S=a·b$, где $а$ и $b$ — смежные стороны.

Ромб — это параллелограмм, у которого все стороны равны.

Все свойства параллелограмма.
Диагонали ромба пересекаются под прямым углом. BD⊥AC.
Диагонали ромба являются биссектрисами углов.

1. Площадь ромба равна половине произведения его диагоналей.

$S=/$, где $d_1$ и $d_2$ — диагонали ромба

2. Площадь ромба равна произведению квадрата стороны на синус острого угла ромба.

$S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.

Квадрат – это прямоугольник, у которого все стороны равны.

Все свойства прямоугольника.
Все свойства ромба.

$S=a^2$, где $а$ — сторона квадрата.
$S=/2$, где $d$ — диагональ квадрата.

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие нет.

Параллельные стороны называются основаниями: $ВС$ и $AD$ — основания.

Непараллельные стороны называются боковыми сторонами: $АВ$ и $CD$ – боковые стороны.

Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.

Свойства средней линии трапеции:

1. Средняя линия параллельна основаниям трапеции.

2. Средняя линия равна полусумме оснований.

3. Диагональ делит среднюю линию на две части, каждая из которых является средней линией получившихся треугольников.

$МК$ — средняя линия треугольника $ABD; MK=/$.

$KN$ — средняя линия треугольника $BCD; KN=/$.

Трапеция, у которой боковые стороны равны, называется равнобедренной.

Свойства равнобедренной трапеции:

1. Углы при основаниях равны.

2. Диагонали в равнобедренной трапеции равны.

3. Основание высоты равнобедренной трапеции, опущенной из меньшего основания, делит другое основание на отрезки, больший из которых равен полусумме оснований.

4. Основания высот равнобедренной трапеции, опущенных из меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований.

5. Если трапеция является равнобедренной, то около неё можно описать окружность.

6. Если в равнобедренной трапеции диагонали пересекаются под прямым углом, то высота рана длине средней линии данной трапеции.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

Два многоугольника называются подобными, если их углы соответственно равны, а стороны одного многоугольника больше сходственных сторон другого многоугольника в некоторое число раз.

Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного многоугольника больше сторон другого многоугольника.)

Периметры подобных многоугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
Отношение площадей двух подобных многоугольников равно квадрату коэффициента подобия.

Часто встречаются задания, в которых на клетчатой бумаге изображен многоугольник и надо найти его площадь. Площадь можно вычислить несколькими способами:

Можно определить по рисунку тип многоугольника и по известным формулам найти площадь.
Площадь искомой фигуры можно найти по формуле Пика:

$S=/+В-1$, где $Г$ — количество узлов на границе фигуры (на сторонах и вершинах);

$В$ — количество узлов внутри фигуры.

Узел — это уголок клетки или пересечение линий

Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки $1$ см $×$ $1$ см. Ответ дайте в квадратных сантиметрах.

Отметим красными точками узлы на границе фигуры (Г), а желтыми – узлы внутри фигуры (В).

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Геометрическая фигура многоугольник

Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.

Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.

Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.

Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.

Видео:Многоугольники. 8 класс.Скачать

Основные понятия

Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:

Если вершины являются концами одной стороны, они называются соседними.
Если отрезок соединяет между собой несоседние вершины, то он имеет название диагонали. У треугольника не может быть диагоналей.
Внутренний угол — это угол при одной из вершин, который образован двумя его сторонами, сходящимися в этой точке. Он всегда располагается во внутренней области геометрической фигуры. Если многоугольник невыпуклый, его размер может превосходить 180 градусов.
Внешний угол при определенной вершине — это угол смежный с внутренним при ней же. Иными словами, внешним углом можно считать разность между 180° и величиной внутреннего угла.
Сумма величин всех отрезков носит название периметра.
Если все стороны и все углы равны — он носит название правильного. Правильными могут быть только выпуклые.

Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:

Многоугольник называется плоским, если ограничивает конечную часть плоскости. Эта геометрическая фигура может быть вписанной в окружность или описанной вокруг окружности.
Выпуклым называется n-угольник, который соответствует одному из условий, приведенных ниже.
Фигура расположена по одну сторону от прямой линии, которая соединяет две соседних вершины.
Эта фигура служит общей частью или пересечением нескольких полуплоскостей.
Диагонали располагаются внутри многоугольника.
Если концы отрезка располагаются в точках, которые принадлежат многоугольнику, весь отрезок принадлежит ему.
Фигура может называться правильной, если у нее все отрезки и все углы равны. Примерами могут служить квадрат, равносторонний треугольник или правильный пятиугольник.
Если n-угольник невыпуклый, все стороны и углы его равны, а вершины совпали с таковыми правильного n-угольника, он называется звездчатым. У таких фигур могут иметься самопересечения. Примерами могут служить пентаграмма или гексаграмма.
Треугольник или четырехугольник называется вписанным в окружность, когда все его вершины располагаются внутри одной окружности. Если же стороны этой фигуры имеют точки соприкосновения с окружностью, это многоугольник описанным около некоторой окружности.

Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Виды фигур

Треугольник

Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.

Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.

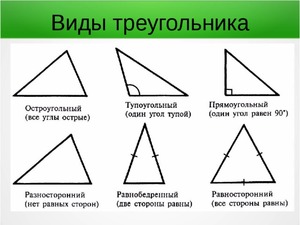
По соотношениям между сторонами все треугольники можно подразделять на несколько видов:

Равносторонние — у которых длина всех отрезков одинаковая.
Равнобедренные — треугольники, у которых равны два отрезка из трех.
Разносторонние — если длина всех отрезков разная.

Кроме того, принято различать следующие треугольники:

Остроугольные.
Прямоугольные.
Тупоугольные.

Четырехугольник

Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.

Если все углы четырехугольника прямые — эта фигура называется прямоугольником.
Прямоугольник, у которого все стороны имеют одинаковую величину, называется квадратом.
Четырехугольник, все стороны которого равны, называется ромбом.

На одной прямой не может находиться сразу три вершины четырехугольника.

Видео:Видеоурок 10. Многоугольники. Математика 1 классСкачать