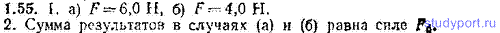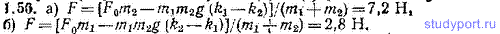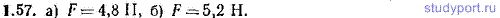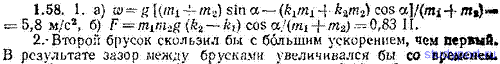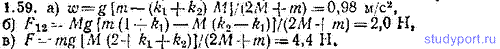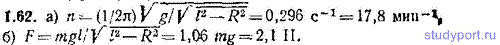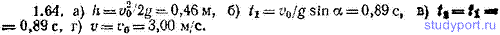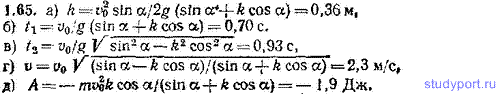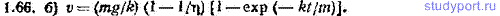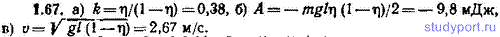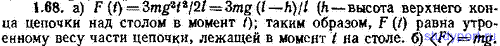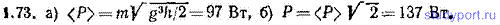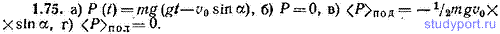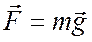1.54. Чтобы определить коэффициент трения k между деревянными поверхностями, брусок положили на доску и стали поднимать один конец доски до тех пор, пока брусок не начал по ней скользить. Это произошло при угле наклона доски α = 14°. Чему равен k?
1.55. Два соприкасающихся бруска лежат на горизонтальном столе, по которому они могут скользить без трения. Масса первого бруска m1=2,00 кг, масса второго бруска m2=3,00 кг. Один из брусков толкают с силой F0=10,0 Н (рис. 1.9). Найти: 1. Силу F, с которой бруски давят друг на друга в случае, если сила F0, приложена к бруску 1 (а), к бруску 2 (б). 2. Что примечательного в полученных результатах?
1.56. Решить задачу 1.55 в предположении, что коэффициент трения между бруском и столом равен k1=0,100 для бруска 1 и k2=0,200 для бруска 2.
1.57. Решить задачу 1.56, положив k1=0,200 и k2=0,100. Сопоставить результаты задач 1.55, 1.56 и данной задачи.
1.58. Два соприкасающихся бруска скользят по наклонной доске (рис. 1.10). Масса первого бруска m1=2,00 кг, масса второго бруска m2=3,00 кг. Коэффициент трения между бруском и доской равен k1=0,100 для бруска 1 и k2=0,200 для бруска 2. Угол наклона доски α=45°. 1. Определить: а) ускорение ω, с которым движутся бруски, б) силу F, с которой бруски давят друг на друга. 2. Что происходило бы в случае k1>k2?
1.59. На горизонтальном столе лежат два тела массой M=1,000 кг каждое. Тела связаны невесомой нерастяжимой нитью (рис. 1.11). Такая же нить связывает тело 2 с грузом массы m=0,500 кг. Нить может скользить без трения по изогнутому желобу, укрепленному на краю стола. Коэффициент трения первого тела со столом k1=0,100, второго тела k2=0,150. Найти: а) ускорение ω, с которым движутся тела, б) натяжение F12 нити, связывающей тела 1 и 2, в) натяжение F нити, на которой висит груз.
1.60. Эстакада на пересечении улиц имеет радиус кривизны R=1000 м. В верхней части эстакады в дорожное покрытие вмонтированы датчики, регистрирующие силу давления на эстакаду. Отмечающий эту силу прибор проградуирован в кгс (1 кгс=9,81 Н). Какую силу давления F показывает прибор в момент, когда по эстакаде проезжает со скоростью v=60,0 км/ч автомобиль массы m=1,000 т?
1.61. На заряженную частицу, движущуюся в магнитном поле, действует магнитная сила F=q [vB] (q — заряд частицы, v — ее скорость, B — характеристика поля, называемая магнитной индукцией). Найти уравнение траектории, по которой будет двигаться частица в однородном магнитном поле (т. е. поле, во всех точках которого В одинакова по модулю и направлению) в случае, если в начальный момент вектор v перпендикулярен к В. Никаких сил, кроме магнитной, нет. Известными считать массу m, заряд q и скорость v частицы, а также магнитную индукцию поля B. В качестве координатной плоскости x, y взять плоскость, в которой движется частица.
1.62. Шарик массы m=0,200 кг, привязанный к закрепленной одним концом нити длины l=3,00 м, описывает в горизонтальной плоскости окружность радиуса R= 1,00 м. Найти: а) число оборотов n шарика в минуту, б) натяжение нити F.
1.63. Горизонтально расположенный диск вращается вокруг проходящей через его центр вертикальной оси с частотой n=10,0 об/мин. На каком расстоянии r от центра диска может удержаться лежащее на диске небольшое тело, если коэффициент трения k=0,200?
1.64. Небольшому телу сообщают начальный импульс, в результате чего оно начинает двигаться поступательно без трения вверх по наклонной плоскости со скоростью v0=3,00 м/с. Плоскость образует с горизонтом угол α=20,0°. Определить: а) на какую высоту h поднимется тело, б) сколько времени t1 тело будет двигаться вверх до остановки, в) сколько времени t2 тело затратит на скольжение вниз до исходного положения, г) какую скорость v имеет тело в момент возвращения в исходное положение.
1.65. Решить задачу 1.64 в предположении, что коэффициент трения между телом и плоскостью k=0,100. Масса тела m=1,00 кг. Помимо указанных в предыдущей задаче величин, определить: д) какую работу А совершает сила трения на всем пути снизу вверх и обратно. Сравнить результаты задачи 1.64 и данной задачи.
1.66. Шарик массы m помещен в высокий сосуд с некоторой жидкостью и отпущен без толчка. Плотность жидкости в η раз меньше плотности шарика. При движении шарика возникает сила сопротивления среды, пропорциональная скорости движения: F=-kv. а) Описать качественно характер движения шарика. б) Найти зависимость скорости шарика v от времени t.
1.67. Тонкая стальная цепочка с очень мелкими звеньями, имеющая длину l=1,000 м и массу m=10,0 г, лежит на горизонтальном столе. Цепочка вытянута в прямую линию, перпендикулярную к краю стола. Конец цепочки свешивается с края стола. Когда длина свешивающейся части составляет η=0,275 длины l, цепочка начинает соскальзывать со стола вниз. Считая цепочку однородной по длине, найти: а) коэффициент трения k между цепочкой и столом, б) работу А сил трения цепочки о стол за время соскальзывания, в) скорость v цепочки в конце соскальзывания.
1.68. Тонкая стальная цепочка с очень мелкими звеньями висит вертикально, касаясь нижним концом стола. Масса цепочки m, длина l. В момент t=0 цепочку отпускают. Считая цепочку однородной по длине, найти: а) мгновенное значение F(t) силы, с которой цепочка действует на стол, б) среднее значение этой силы за время падения.
1.69. Сила, действующая на частицу, имеет вид F=aex(H), где a — константа. Вычислить работу А, совершаемую над частицей этой силой на пути от точки с координатами (1, 2, 3) (м) до точки с координатами (7, 8, 9) (м).
1.70. Частица движется равномерно по окружности. Чему равна работа А результирующей всех сил, действующих на частицу: а) за один оборот, б) за полоборота, в) за четверть оборота?
1.71. Частица перемещается по окружности радиуса r под действием центральной силы F. Центр окружности совпадает с силовым центром. Какую работу А совершает сила F на пути s?
1.72. Тангенциальное ускорение wτ частицы массы m, движущейся по некоторой криволинейной траектории, изменяется с расстоянием s, отсчитанным вдоль траектории от некоторого начального положения частицы, по закону ωτ=ωτ(s). Написать выражение для работы A, совершаемой над частицей всеми действующими на нее силами, на участке траектории от s1 до s2.
1.73. Тело массы m=1,00 кг падает с высоты h=20,0 м. Пренебрегая сопротивлением воздуха, найти: а) среднюю по времени мощность
, развиваемую силой тяжести на пути h, б) мгновенную мощность P на высоте h/2.
1.74. Брошенный камень массы m поднимается над уровнем, на котором находится точка бросания, на высоту h. В верхней точке траектории скорость камня равна v. Сила сопротивления воздуха совершает над камнем на пути от точки бросания до вершины траектории работу Aсопр. Чему равна работа A бросания камня?
1.75. Тело массы m брошено под углом α к горизонту с начальной скоростью v0. Пренебрегая сопротивлением воздуха, найти: а) мгновенную мощность P(t), развиваемую при полете тела приложенной к нему силой, б) значение мощности P в вершине траектории, в) среднее значение мощности
под за время подъема тела, г) среднее значение мощности
пол за все время полета (точка бросания и точка падения находятся на одном уровне).
1.76. Тело массы m начинает двигаться под действием силы F=2tex+3t 2 ey. Найти мощность P(t), развиваемую силой в момент времени t.
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
- Работа и энергия. Работа, мощность. Консервативные и диссипативные силы. Кинетическая и потенциальная энергия механической системы. Закон сохранения энергии
- Страницы работы
- Фрагмент текста работы
- 1.2 — Динамика материальной точки и поступательного движения тела. Работа и мощность
- UptoLike
- Решебник Савельева (1988) — Задача 1. 76
- Решебник Савельева (1988) — Задача 1. 75
- Решебник Савельева (1988) — Задача 1. 74
- Решебник Савельева (1988) — Задача 1. 73
- Решебник Савельева (1988) — Задача 1. 72
- Решебник Савельева (1988) — Задача 1. 71
- Решебник Савельева (1988) — Задача 1. 70
- Решебник Савельева (1988) — Задача 1. 69
- Решебник Савельева (1988) — Задача 1. 68
- Решебник Савельева (1988) — Задача 1. 67
- 🎦 Видео
Видео:Физика - движение по окружностиСкачать

Работа и энергия. Работа, мощность. Консервативные и диссипативные силы. Кинетическая и потенциальная энергия механической системы. Закон сохранения энергии
Страницы работы
Фрагмент текста работы
ТЕМА 9 РАБОТА И ЭНЕРГИЯ
1 Работа, мощность.
2 Консервативные и диссипативные силы.
3 Кинетическая и потенциальная энергия механической системы.
4 Закон сохранения энергии.
Вопросы для самоподготовки
1 Напишите различные возможные варианты выражения для работы. Поясните смысл величин входящих в эти выражения.
2 В каких единицах измеряются работа и мощность в системе СИ? Дайте определения этих единиц. 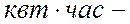
3 Сформулируйте теорему об изменении кинетической энергии.
4 Частица движется равномерно по окружности. Чему равна работа равнодействующей всех сил, действующих на частицу: а) за один оборот, б) за половину оборота, в) за четверть оборота?
5 Какие силы называют консервативными? диссипативными? Приведите примеры консервативных и диссипативных сил.
6 Дайте определение потенциальной энергии. Чем она обусловлена?
7 Почему потенциальная энергия может быть определена только с точностью до некоторой постоянной? Что это за постоянная?
8 Как следует понимать выражение «Потенциальная энергия является функцией состояния системы»?
9 Сформулируйте закон сохранения энергии. Почему в механике рассматривают только два вида энергии — кинетическую и потенциальную?
10 Приведите пример замкнутой механической системы, в которой закон сохранения механической энергии не выполняется.
Основные понятия по теме
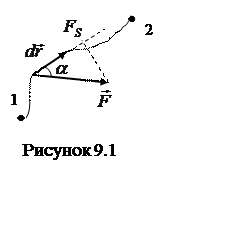
Пусть под действием силы 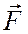
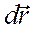
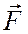
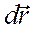
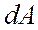
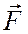
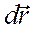
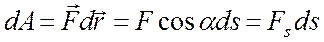
Здесь 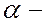
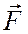
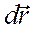
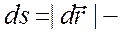
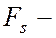
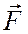
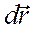
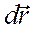
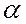
В общем случае работа силы 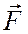
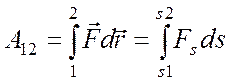
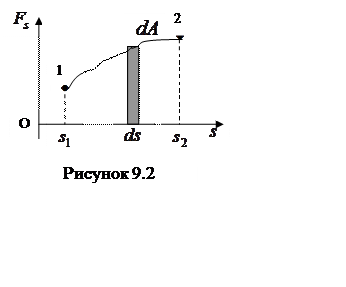
Выражение (9.2) имеет наглядный геометрический смысл. Если зависимость 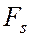
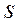
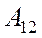
Для характеристики скорости, с которой совершается работа, вводят понятие мощности. Мощность 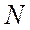
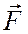
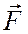
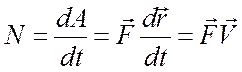
Таким образом, мощность, развиваемая силой 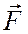
Вычисление работы конкретных сил по формуле (9.2) показывает, что работа некоторых из них не зависит от формы траектории и определяется только начальным 1 и конечным 2 положениями точки. Силы, обладающие таким свойством, называются консервативными. Примерами таких сил могут служить:
— сила тяжести
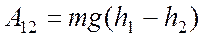
— сила упругости
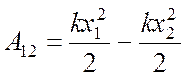
Очевидно, что работа консервативных сил на любом замкнутом пути равна нулю.
Все силы, не являющиеся консервативными, называются неконсервативными. Важным примером неконсервативных сил могут служить диссипативные силы, к которым относятся силы трения и сопротивления. Работа этих сил зависит от пути между начальным и конечным положениями точки и не равна нулю на любом замкнутом пути.
Независимость работы консервативных сил от пути между точками 1 и 2 позволяет ввести для этих сил понятие потенциальной энергии.
Потенциальной энергией тела в состоянии 1 называют величину равную работе по перемещению тела из этого состояния в «бесконечность» под действием только консервативных сил
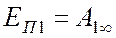
Термин «бесконечность» в данном определении имеет условный смысл. Им обозначено состояние тела в котором его потенциальная энергия принята равной нулю.
Вычислим работу, совершаемую при перемещении тела из состояния 1 в состояние 2 (рисунок 9.3). Учитывая тот факт, что работа консервативных сил не зависит от пути, получаем
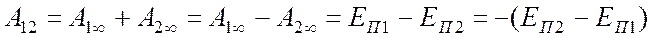
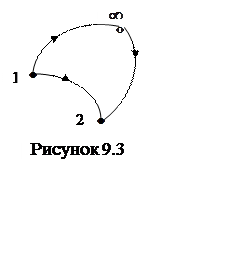
Приведенная выше формулировка (9.6) определяет потенциальную энергию тела в поле консервативных сил. При этом сила и потенциальная энергия связаны соотношением
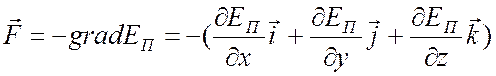
Потенциальная энергия взаимодействующих тел определяется их взаимным расположением и характером сил взаимодействия между ними.
Помимо потенциальной энергии в механике рассматривается кинетическая энергия. Кинетическая энергия – это энергия движения тела. Она зависит только от массы и скорости тела. Для точечного тела
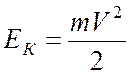
Связь кинетической энергии и работы устанавливает теорема об изменении кинетической энергии: изменение кинетической энергии тела при его перемещении из состояния 1 в состояние 2 равно работе всех сил приложенных к телу на этом перемещении
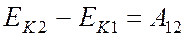
Сумму кинетической и потенциальной энергий называют полной механической энергией
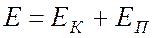
Записав выражения аналогичные (9.7) и (9.10) для системы тел, нетрудно получить, что для произвольно выбранных состояний 1 и 2
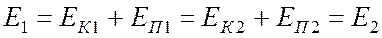
Соотношение (9.12) выражает закон сохранения энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия не изменяется
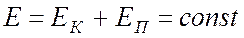
Закон сохранения энергии является следствием однородности времени – инвариантности физических законов относительно выбора начала отсчета времени.
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

1.2 — Динамика материальной точки и поступательного движения тела. Работа и мощность
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

UptoLike
Задачи из раздела « Динамика материальной точки и поступательного движения тела. Работа и мощность » сборника по общему курсу физики И.В. Савельева. Решение задач можно скачать в 1 клик.
Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Решебник Савельева (1988) — Задача 1. 76
Тело массы m начинает двигаться под действием силы F = 2tex + 3t2ey. Найти мощность P(t), развиваемую силой в момент времени t.
Видео:Вращательное движение. 10 класс.Скачать

Решебник Савельева (1988) — Задача 1. 75
Тело массы m брошено под углом a к горизонту с начальной скоростью v0.
Видео:Центростремительное ускорение. 9 класс.Скачать

Решебник Савельева (1988) — Задача 1. 74
Брошенный камень массы m поднимается над уровнем, на котором находится точка бросания, на высоту h. В верхней точке траектории скорость камня равна v. Сила сопротивления воздуха совершает над камнем на пути от точки бросания до вершины траектории работу Aсопр.
Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Решебник Савельева (1988) — Задача 1. 73
Тело массы m = 1,00 кг падает с высоты h = 20,0 м. Пренебрегая сопротивлением воздуха, найти: а) среднюю по времени мощность (Р), развиваемую силой тяжести на пути h, б) мгновенную мощность Р на высоте h/2.
Видео:Движение по окружности | Физика в анимациях | s01e07Скачать

Решебник Савельева (1988) — Задача 1. 72
Тангенциальное ускорение wт частицы массы m, движущейся по некоторой криволинейной траектории, изменяется с расстоянием s, отсчитанным вдоль траектории от некоторого начального положения частицы, по закону wт = wт(s).
Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Решебник Савельева (1988) — Задача 1. 71
Частица перемещается по окружности радиуса r под действием центральной силы F. Центр окружности совпадает с силовым центром. Какую работу А совершает сила F на пути s?
Видео:Физика - уравнения равноускоренного движенияСкачать

Решебник Савельева (1988) — Задача 1. 70
Частица движется равномерно по окружности. Чему равна работа А результирующей всех сил, действующих на частицу: а) за один оборот, б) за полоборота, в) за четверть оборота?
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Решебник Савельева (1988) — Задача 1. 69
Сила, действующая на частицу, имеет вид F = аех(Н), где а — константа. Вычислить работу A, совершаемую над частицей этой силой на пути от точки с координатами (1, 2, 3) (м) до точки с координатами (7, 8, 9) (м).
Видео:Физика | Равномерное движение по окружностиСкачать

Решебник Савельева (1988) — Задача 1. 68
Тонкая стальная цепочка с очень мелкими звеньями висит вертикально, касаясь нижним концом стола. Масса цепочки m, длина l. В момент t = 0 цепочку отпускают.
Видео:Лекция 10. Угловая скорость и угловое ускорение │Физика с нуляСкачать

Решебник Савельева (1988) — Задача 1. 67
Тонкая стальная цепочка с очень мелкими звеньями, имеющая длину l = 1,000 м и массу m = 10,0 г, лежит на горизонтальном столе. Цепочка вытянута в прямую линию, перпендикулярную к краю стола. Конец цепочки свешивается с края стола.
🎦 Видео
Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Угловая скорость и радианная мера углаСкачать

Урок 89. Движение по окружности (ч.1)Скачать

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Физика 9 класс. Движение по окружностиСкачать

Тема 12. Ускорение точки при ее движении по окружностиСкачать