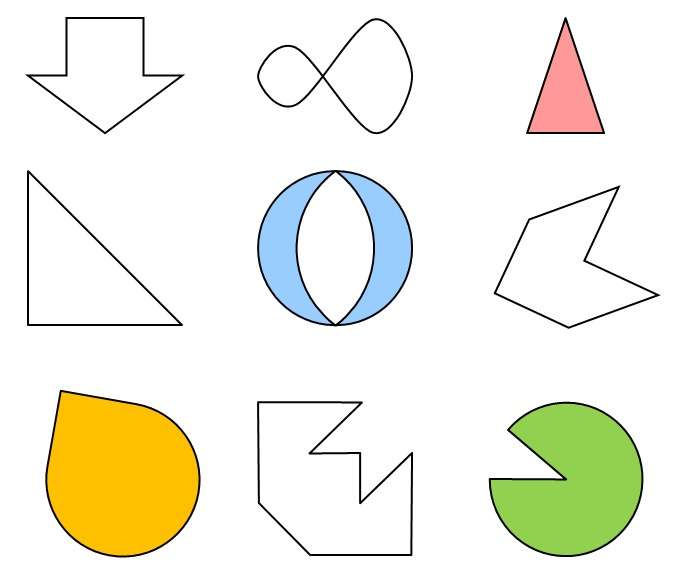
Что же такое ось симметрии? Это множество точек, которые образуют прямую, являющуюся основой симметрии, то есть, если от прямой отложили определенное расстояние с одной стороны, то оно отразится и в другую сторону в таком же размере. Осью может выступать все, что угодно, — точка, прямая, плоскость и так далее. Но об этом лучше говорить на наглядных примерах.
Видео:Ось симметрииСкачать

Симметрия
Для того чтобы понять, что такое ось симметрии, нужно вникнуть в само определение симметрии. Это соответствие определенного фрагмента тела относительно какой-либо оси, когда его структура неизменна, а свойства и форма такого объекта остаются прежними относительно его преобразований. Можно сказать, что симметрия — свойство тел к отображению. Когда фрагмент не может иметь подобного соответствия, это называется асимметрией или же аритмией.

Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Видео:Ось симметрии. Что это такое и как её проводить?Скачать

Виды симметрии
Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:
Видео:№417. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?Скачать

История симметрии
Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.
В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.
А философ Платон считал многогранники олицетворением четырех природных стихий:
- тетраэдр — огонь, так как его вершина направлена вверх;
- куб — земля, так как это самое устойчивое тело;
- октаэдр — воздух, нет каких-либо объяснений;
- икосаэдр — вода, так как тело не имеет грубых геометрических форм, углов и так далее;
- образом всей Вселенной являлся додекаэдр.
Из-за всех этих теорий правильные многогранники называют телами Платона.
Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.
Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».
Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».
Что уж там говорить, симметрия — ключевое понятие для всех деятелей искусства на протяжении многих веков, но в XX веке ее смысл оценили также все деятели точных наук. Точным свидетельством являются физические и космологические теории, например, теория относительности, теория струн, абсолютно вся квантовая механика. Со времен Древнего Вавилона и, заканчивая передовыми открытиями современной науки, прослеживаются пути изучения симметрии и открытия ее основных законов.
Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника — также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно — длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.
Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых — бесконечное множество.
У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии — диагонали, а во втором — средние линии. Множество таковых осей только у квадрата.
Видео:Прямоугольник. Ось симметрии. 5 классСкачать

Симметрия в природе
Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.
А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия — основное условие.
Видео:Центральная симметрия. 6 класс.Скачать

Вывод
Нас постоянно окружают какие-либо явления и предметы, например, радуга, капля, цветы, лепестки и так далее. Их симметрия — очевидна, в какой-то степени она обусловлена гравитацией. Часто в природе под понятием «симметрия» понимают регулярную смену дня и ночи, времен года и так далее.
Подобные свойства наблюдаются везде, где есть порядок и равенство. Также и сами законы природы — астрономические, химические, биологические и даже генетические подчинены определенным принципам симметрии, так как имеют совершенную системность, а значит, сбалансированность имеет всеохватывающий масштаб. Следовательно, осевая симметрия — один из основополагающих законов мироздания в целом.
Видео:Осевая симметрия. 6 класс.Скачать

Учебник Моро 4 класс 1 часть. Страница 67
Упражнения
313. Запиши вычисления в строчку.
18 ч 36 мин — 9 ч = (18 ч — 9 ч) + 36 мин = 9 ч 36 мин
18 ч 36 мин — 9 мин = 18 ч + (36 мин — 9 мин) = 18 ч 27 мин
12 км 065 м + 20 м = 12 км + (65 м + 20 м) = 12 км 85 м
20 мин 30 с + 25 с = 20 мин + (30 с + 25 с) = 20 мин 55 с
2 мин 30 м — 1 мин = (2 мин — 1 мин) + 30 с = 1 мин 30 с
6 м 20 см + 75 см = 6 м + (20 см + 75 см) = 6 м 95 см
314. Запиши вычисления столбиком
315. В трёх составах 120 товарных вагонов. В первом и втором составах вместе 77 вагонов, во втором и третьем — 70 вагонов. Сколько вагонов в каждом составе? Сделай чертёж к задаче и реши её.
1) 120 — 70 = 50 (шт.) — вагонов в первом составе.
2) 120 — 77 = 43 (шт.) — вагонов во третьем составе.
3) 70 — 43 = 27 (шт.) — вагонов во втором составе.
Ответ: 50, 27 и 43 вагона.
316. На видеокассету, рассчитанную на 210 мин, записали два фильма: первый длится 1 ч 38 мин, второй — 1 ч 27 мин. Можно ли на эту кассету записать ещё один фильм, который длится 23 мин?
1) 1 ч 38 мин + 1 ч 27 мин + 23 мин = 98 мин + 87 мин + 23 мин = 208 мин — заняли бы все три фильма.
317. Реши:
318. 1) Найди площадь и периметр треугольника ACD.
Найдём площадь треугольника
Прямоугольник MBCD состоит из четырёх треугольников. Значит можно сказать, что площадь прямоугольника равна сумме площадей треугольников 1, 2, 3 и 4.
- треугольник 1 = треугольнику 2, S(ABC) = S(ACK)
- треугольник 3 = треугольнику 4, S(AMD) = S(ADK)
Значит можно записать: S (ACK) + S (AKD) = S (MBCD) : 2
- S (ACD) = S (ACK) + S (AKD) = S (MBCD) : 2 = 8 • 3 : 2 = 24 : 2 = 12 см²
Найдём периметр треугольника
Периметр — это сумма длин всех сторон треугольника.
- P = 42 + 58 + 80 = 100 + 80 = 180 мм = 18 см.
2) Будет ли отрезок АК его осью симметрии?
Нет, так как прямоугольник ABCK не равен квадрату AKDM.
Видео:Осевая и центральная симметрия, 6 классСкачать

Осевая и центральная симметрии
Если прямая 


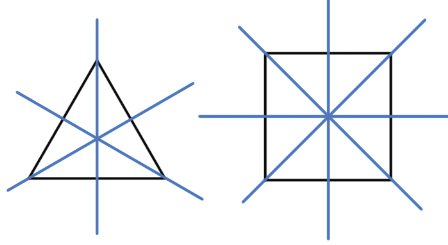
Фигура называется симметричной относительно прямой 


Пример (синим цветом обозначены оси симметрии):
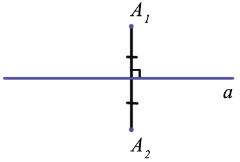
Точки А1 и А2 называются симметричными относительно точки О, если О — середина отрезка А1А2. Точка О считается симметричной самой себе.
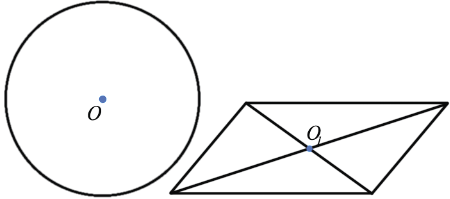
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры.
Пример (синим цветом обозначены центры симметрии):
Поделись с друзьями в социальных сетях:
📹 Видео
Оси симметрии прямоугольника, равнобедренного треугольника, окружностиСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Геометрия на С++. Поиск осей симметрии выпуклого четырехугольникаСкачать

6 класс, 26 урок, СимметрияСкачать

Математика 5 класс. Ось симметрии фигурыСкачать

Вершина параболы и ось симметрии. ПримерСкачать

Симедиана. Гармонические четырехугольники. | Олимпиадная математикаСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

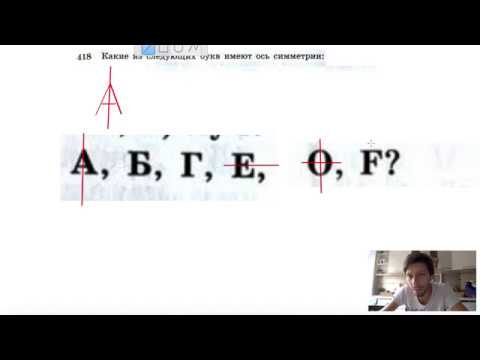
№418. Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О, F?Скачать
3 правила для вписанного четырехугольника #shortsСкачать

Осевая симметрия, как начертить треугольники симметричноСкачать