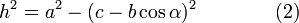1. Свойство углов, образованных при пересечении двух параллельных прямых третьей прямой (формулировки и примеры)
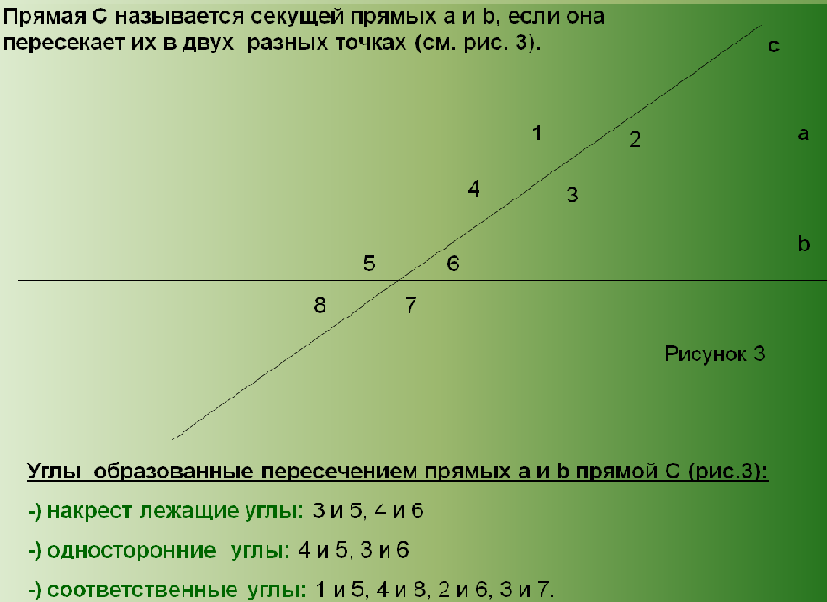
При пересечении двух прямых секущей, образуется 8 уг-
лов. На рисунке 8 обозначим их цифрами.
Углы 3 и 5, 4 и 6 — накрест лежащие;
Углы 4 и 5, 3 и 6 — односторонние;
Углы 1 и 5, 4 и 8, 2 и 6, 3 и 7 — соответственные.
Если прямые а и Ь на рис.8 параллельны, то эти углы
имеют специальные свойства:
Теорема: Если две параллельные прямые пересечены се-
кущей, то накрест лежащие углы равны.
Теорема: Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Теорема: Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°
2. Решение треугольника по двум сторонам и углу между ними.
Решением треугольника называется нахождение всех его шести элементов (трех сторон и трех углов) по каким-нибудь трем заданным элементам, определяющим треугольник.
Решение треугольника по двум сторонам и углу между ними
То есть мы нашли три неизвестных элемента треугольника, а значит, решили треугольник.
3. Задача по теме »Средняя линия треугольника» (типа №46-48)
№46. В треугольнике ABC отмечены точки D и E, которые являются серединами сторон AB и BC соответственно Найдите периметр четырехугольника ADEC, если AB=24 см, BC=32 см и АС=44 см
DE — средняя линия треугольника ABC по определению. По свойству средней линии (средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьем стороне и равна ее половине)
Периметр четырехугольника ADEC равен
№ 47 . Диагональ квадрата равна 26 см. Найдите периметр
четырехугольника, вершинами которого являются середи-
ны сторон квадрата.
Периметр четырехугольника EFGH равен EF+FG+GH+HE=4EF=4*13=52 cм.
№ 48 . В равностороннем треугольнике QRP отмечены точки S, T и O, которые являются серединами сторон QR, RP и QP соответственно. Найдите периметр параллелограмма QSTO, если периметр треугольника SRT равен 27 см.
ST — средняя линия треугольника QRP, по свойству средней линии она параллельна QP и равна . Треугольники следовательно, т. SPT — равносторонний , и SR=RT=ST, его периметр равен SR+RT+ST= 27 см, откуда получаем, что 3SR=27 cм; SR=9см=RT=ST. QO= = ST=9 см; QS= =SR=9 см. В параллелограмме противоположные стороны равны, значит, SQ=TO. Следовательно, периметр параллелограмма QSTO равен ST+TO+OQ+QS=36см.
4. Задача по теме «Неравенство треугольника»
(типа № 44)
№ 44. Расстояние от точки А до точек В и С равны 3 см и
14 см соответственно, а расстояния от точки D до точек
В и С равны 5 см и б см соответственно. Докажите, что
точки А, В, С и D лежат на одной прямой.
AC=14, AB=3, CD=6, BD=5 (см)
Проведем отрезок AC. Проведем окружность с центром в точке A радиуса 3 см. Точка B лежит на этой окружности. При этом AM=3 cм. Проведем окружность с центром в точке С радиуса 6 см. Точка D лежит на этой окружности. При этом CN=6 см. Тогда MN=AC-AM-CN=5 см. Теперь видим, что BD=5см, тогда и только тогда, когда точки B и D лежат на отрезке AC. Что и требовалось доказать.
Видео:№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

ГЕОМЕТРИЯ 9 класс
Билет № 1
1. Углы, образованные при пересечении двух параллельных прямых третьей прямой. Свойство внутренних односторонних углов.
2. Треугольник: определение и виды. Теорема косинусов (доказательство). Следствия из теоремы косинусов.
3. Найдите диагонали равнобедренной трапеции, основания которой равны 4 см и 6 см, а боковая сторона равна 5 см.
4. В окружности радиуса 6 см проведена хорда АВ. Через середину М этой хорды проходит прямая, пересекающая окружность в точках С и Е. Известно, что СМ = 9 см, —>
- >» src=»http://narod2.yandex.ru/i/users/color/red/arrow-s3.png» />Главная
- >» src=»http://narod2.yandex.ru/i/users/color/red/arrow-s3.png» />Билет 1
- >» src=»http://narod2.yandex.ru/i/users/color/red/arrow-s3.png» />Билет 2
1) Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Вертикальные углы — два угла, которые образуются при пересечении двух прямых, эти углы не имеют общих сторон. Другими словами — два угла называют вертикальными, если стороны одного угла являются продолжениями сторон другого. Два вертикальных угла равны.
 Свойство внутренних односторонних углов:
Свойство внутренних односторонних углов:
Если при пересечении двух прямых, лежащих в одной плоскости, третьей прямой углы одной из пар соответственных или накрест лежащих углов равны, то сумма углов каждой пары односторонних углов равна 180 градусов.
2) Треуго́льник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки
| Типы треугольников | ||
|---|---|---|
 Остроугольный |  Тупоугольный |  Прямоугольный |
 Разносторонний |  Равнобедренный | 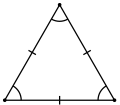 Равносторонний |
По величине углов
Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми(меньшими 90°). Выделяют следующие виды треугольников:
- Если все углы треугольника острые, то треугольник называется остроугольным;
- Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
- Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
По числу равных сторон
- Разносторонним называется треугольник, у которого длины трёх сторон различны.
- Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называютсябоковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
- Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.
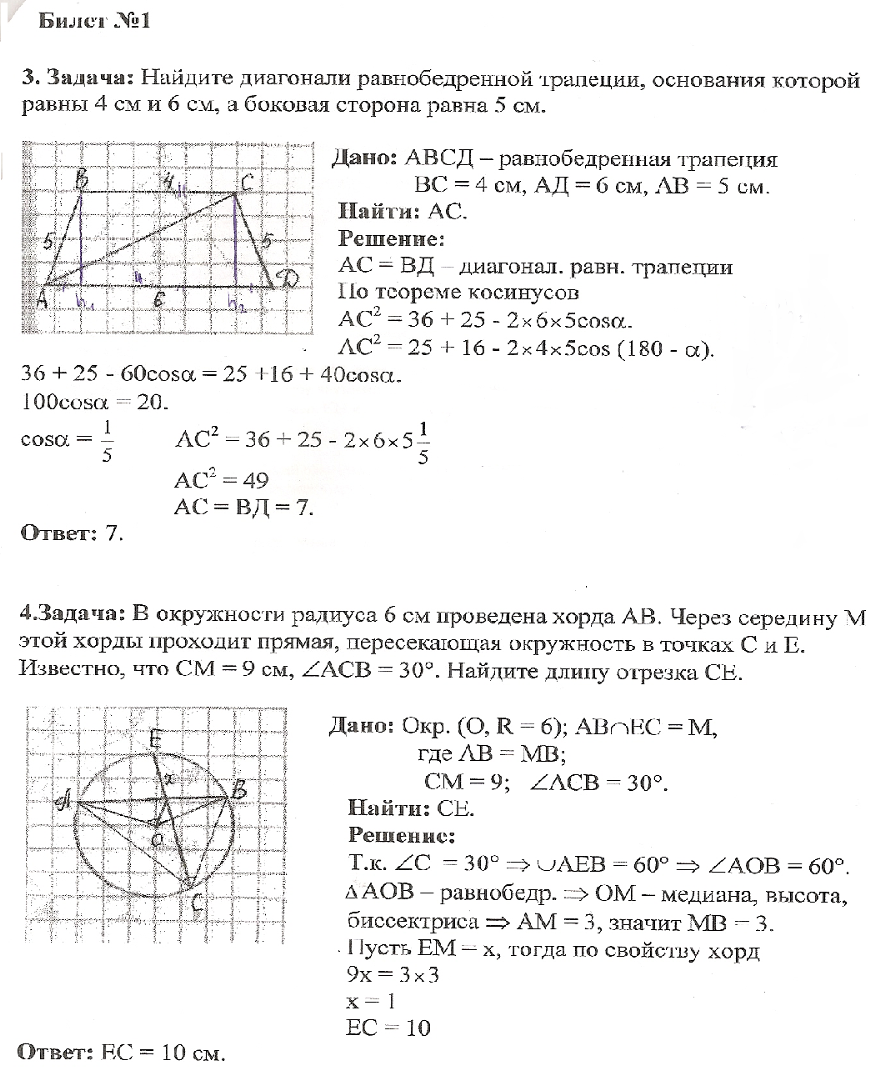
Теорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора:
Для плоского треугольника со сторонами a,b,c и углом α , противолежащим стороне a , справедливо соотношение: 
Рассмотрим треугольник ABC. Из вершины C на сторону AB опущена высота CD. Из треугольника ADC следует:
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
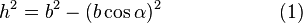
Приравниваем правые части уравнений (1) и (2) и:
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.
Выражения для сторон b и c:
3)
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Углы при пересечении двух прямых
Если какие-нибудь две прямые пересечены третьей прямой, то пересекающая их прямая называется секущей по отношению к прямым, которые она пересекает.
При пересечении двух прямых третьей, образуется два вида углов: внешние и внутренние.
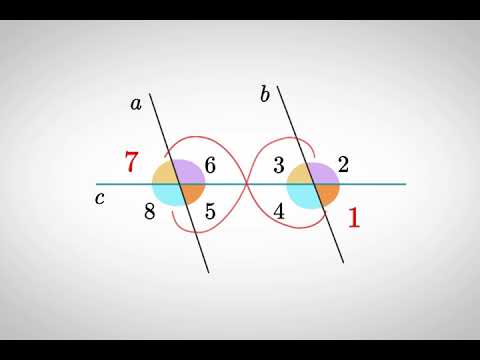
На рисунке изображены две прямые a и b, пересекаемые прямой c. Прямая c по отношению к прямым a и b является секущей. Синим цветом на рисунке обозначены внешние углы (∠1, ∠2, ∠7 и ∠8), а красным — внутренние углы (∠3, ∠4, ∠5 и ∠6).
Также при пересечении двух прямых третьей, образовавшиеся углы получают попарно следующие названия:
| Соответственные углы: ∠1 и ∠5, ∠3 и ∠7, ∠2 и ∠6, ∠4 и ∠8. |  |
| Внутренние накрест лежащие углы: ∠3 и ∠6, ∠4 и ∠5. |  |
| Внешние накрест лежащие углы: ∠1 и ∠8, ∠2 и ∠7. |  |
| Внутренние односторонние углы: ∠3 и ∠5, ∠4 и ∠6. |  |
| Внешние односторонние углы: ∠1 и ∠7, ∠2 и ∠8. |  |
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Углы при пересечении параллельных прямых
Если секущая пересекает две параллельные прямые линии, то:
- внутренние накрест лежащие углы равны;
- сумма внутренних односторонних углов равна 180°;
- соответственные углы равны;
- внешние накрест лежащие углы равны;
- сумма внешних односторонних углов равна 180°.
🌟 Видео
Углы, образованные при пересечении двух прямых секущейСкачать

Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

№208. Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50°Скачать

Углы при пересечении двух прямых третьейСкачать

№201. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210Скачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Задача про углы образованные от пересечения прямых. Геометрия 7 класс.Скачать

Углы, образованные при пересечении двух прямых секущейСкачать

ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ 4. Углы, образованные при пересечении двух параллельных прямых третьейСкачать

Геометрия 7. Углы, образованные при пересечении двух параллельных прямых секущей. Урок на bilimland.Скачать
Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Найти углы образованные при пересечении двух прямых если один из углов на 50 градусов больше другогоСкачать
Углы при пересечении двух прямых секущей (третьей прямой). Виды углов урок 5. Геометрия 7 класс.Скачать

№65. Найдите неразвернутые углы, образованные при пересечении двух прямых,Скачать

ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

УГЛЫ: Односторонние, Накрест Лежащие, Внутренние, Внешние // Теорема об углах — Геометрия 7 классСкачать

7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

 Свойство внутренних односторонних углов:
Свойство внутренних односторонних углов: