Прежде чем приступить к тематике статьи, напомним основные понятия.
Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.
Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.
Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.
- Сложение двух векторов
- Сложение нескольких векторов
- Умножение вектора на число
- Свойства операций над векторами
- Арифметическое n-мерное векторное пространство. Арифметические векторы и их обозначение. Линейно зависимые и линейно независимые системы векторов
- Страницы работы
- Содержание работы
- Глава 8 Арифметическое n-мерное векторное пространство.
- Векторы на ЕГЭ по математике. Действия над векторами
- Сложение векторов
- Вычитание векторов
- Умножение вектора на число
- Скалярное произведение векторов
- Онлайн-курс «Математика 10+11 100 баллов»
- 🎬 Видео
Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

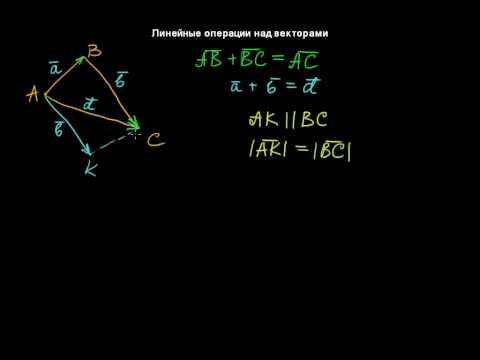
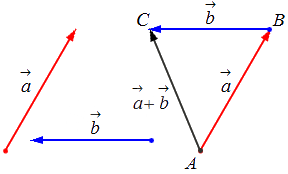
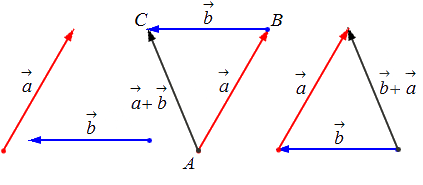
Сложение двух векторов
Исходные данные: векторы a → и b → . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор A B → , равный вектору а → ; из полученной точки undefined – вектор В С → , равный вектору b → . Соединив точки undefined и C , получаем отрезок (вектор) А С → , который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.
Геометрически сложение векторов выглядит так:
— для неколлинеарных векторов:
— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

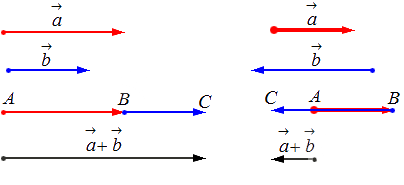
Сложение нескольких векторов
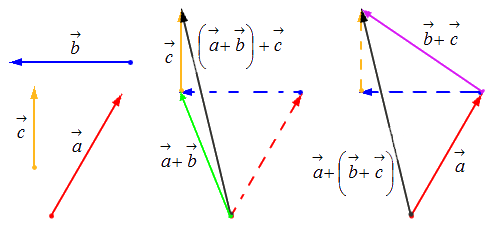
Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.
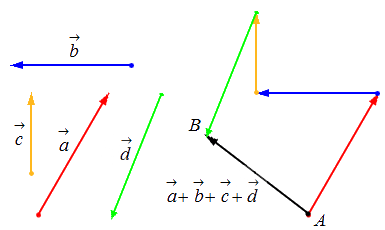
Исходные данные: векторы a → , b → , c → , d → . Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a → ; затем от конца полученного вектора откладывается вектор, равный вектору b → ; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B , а полученный отрезок (вектор) A B → – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .
Геометрически оно выглядит следующим образом:
Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a → и b → есть сумма векторов a → и — b → .
Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

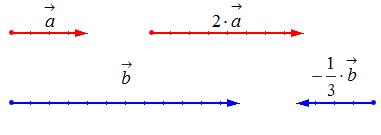
Умножение вектора на число
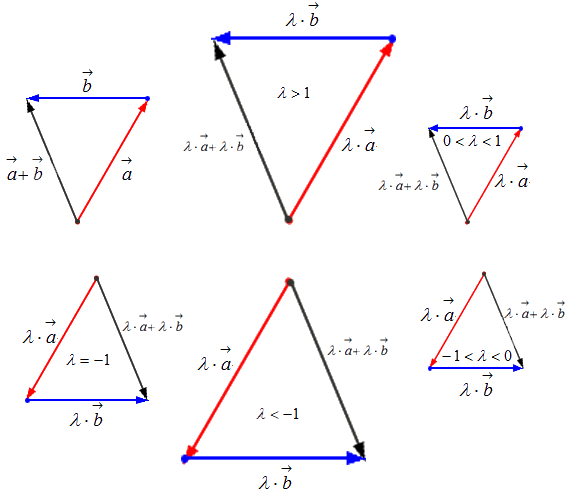
Чтобы произвести действие умножения вектора на некое число k , необходимо учитывать следующие правила:
— если k > 1 , то это число приведет к растяжению вектора в k раз;
— если 0 k 1 , то это число приведет к сжатию вектора в 1 k раз;
— если k 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k = 1 , то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.
Исходные данные:
1) вектор a → и число k = 2 ;
2) вектор b → и число k = — 1 3 .
Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:
Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Свойства операций над векторами
Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.
Исходные данные: векторы a → , b → , c → и произвольные действительные числа λ и μ .
- Свойство коммутативности: a ⇀ + b → = b → + a → .
- Свойство ассоциативности: ( a → + b → ) + c → = a → + ( b → + c → ) .
- Свойство использования нейтрального элемента по сложению (нулевой вектор 0 → ⃗). Это очевидное свойство: a → + 0 → = a →
- Свойство использования нейтрального элемента по умножению (число, равное единице): 1 · a → = a → . Это очевидное свойство, не предполагающее никаких геометрических преобразований.
- Любой ненулевой вектор a → имеет противоположный вектор — a → и верным является равенство: a → + ( — a → ) = 0 → . Указанное свойство — очевидное.
- Сочетательное свойство операции умножения: ( λ · µ ) · a → = λ · ( µ · a → ) . Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
- Первое распределительное свойство (очевидно): ( λ + µ ) · a → = λ · a → + µ · a → .
- Второе распределительное свойство: λ · ( a → + b → ) = λ · a → + λ · b → .
Геометрически это свойство определяется подобием треугольников:
Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.
Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.
Задача: упростить выражение a → — 2 · ( b → + 3 · a → )
Решение
— используя второе распределительное свойство, получим: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · ( 3 · a → )
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a → — 2 · b → — 2 · ( 3 · a → ) = a → — 2 · b → — ( 2 · 3 ) · a → = a → — 2 · b → — 6 · a →
— используя свойство коммутативности, меняем местами слагаемые: a → — 2 · b → — 6 · a → = a → — 6 · a → — 2 · b →
— затем по первому распределительному свойству получаем: a → — 6 · a → — 2 · b → = ( 1 — 6 ) · a → — 2 · b → = — 5 · a → — 2 · b → Краткая запись решения будет выглядеть так: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · 3 · a → = 5 · a → — 2 · b →
Ответ: a → — 2 · ( b → + 3 · a → ) = — 5 · a → — 2 · b →
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Арифметическое n-мерное векторное пространство. Арифметические векторы и их обозначение. Линейно зависимые и линейно независимые системы векторов
Страницы работы
Содержание работы
Глава 8 Арифметическое n-мерное векторное пространство.
Выше мы дали понятие вектора на плоскости и в пространстве.
На плоскости вектор определяется двумя координатами, то есть парой чисел. В пространстве вектор определяется уже тройкой чисел. Причём в этих случаях возможна была геометрическая интерпретация. Во многих задачах экономики приходится встречаться с величинами, которые определяются гораздо большим числом характеристик чем три. Поэтому обобщим понятие вектора на тот случай, когда число характеристик равно n.
Определение 1: Арифметическим n — мерным вектором называется любая последовательность из n действительных чисел:
Обозначать арифметический вектор будем как и обычный вектор чертой сверху, числа а1, а2, …, аn называются компонентами или координатами вектора.
Имеем арифметический вектор с координатами –1, 2, 3, 0, 1.
Многие определения, введённые для векторов, на плоскости и в пространстве фактически обозначаются на случай двух координат. Тем не менее, повторим их.
Определение 2: Дав вектора 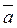
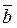
равенство векторов записывают: 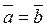
Определение 3: Вектор, у которого все компоненты равны нулю, называется нулевым вектором (0,0,…0).
Обозначается: 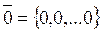
Определение 4: Суммой двух векторов 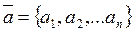
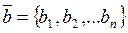
Определение 5: Произведением вектора 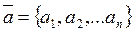
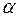
Операции сложения двух арифметических векторов и умножение арифметического вектора на число обладает следующими свойствами.
1. 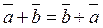
2. 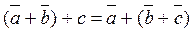
3. 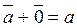
4. Для любого вектора 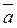
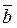
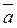
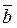
5. 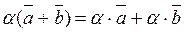
6. 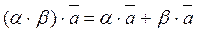
7. 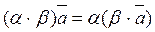
8. 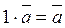
Приведённые свойства почти очевидны и являются следствиями свойств сложения и умножения чисел.
Определение 6: Арифметическим n – мерным пространством называется множество всех n – мерных арифметических векторов с введёнными выше операциями сложения векторов и умножения вектора на число. Обозначается R n .
Очень важным понятием для арифметических векторов является скалярное произведение, но для арифметических векторов оно определяется несколько иначе.
Определение 7: Скалярным произведением двух векторов 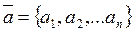
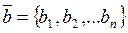
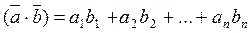
Скалярное произведение обладает теми же свойствами, которые были введены для трёхмерных векторов.
Модуль арифметического n – мерного вектора определяется, так же как и в трёхмерном пространстве.
Аналогично вводится и понятие угла между двумя не нулевыми векторами.
Определение 8: Неравенство Коши-Буияковского. Для любых двух векторов 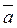
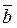
Определение 9: Два арифметических вектора 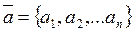
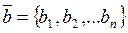
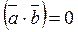
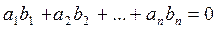
8.2 Линейно зависимые и линейно независимые системы векторов.
Прежде чем ввести понятие линейной зависимости векторов, дадим определение системы векторов.
Определение 1: Если мы имеем дело не с одним, а несколькими векторами, то есть набор векторов 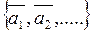
Определение 2: Пусть даны векторы 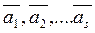
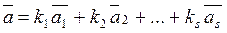
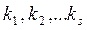
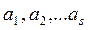
Определение 3: Система векторов 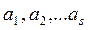
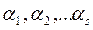
Определение 4: Система векторов 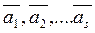
выполняется только в том случае, если все коэффициенты одновременно равны нулю 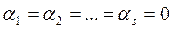
Свойства линейной зависимости.
1. Система из одного вектора линейно зависима тогда и только тогда, когда это нулевой вектор.
2. Система, содержащая более одного вектора, линейно зависима тогда и только тогда, когда среди данных векторов имеется такой, который выражается линейно через остальные.
3. Если часть системы векторов линейно зависима, то и вся система векторов линейно зависима. Таким образом, система, содержащая нулевой вектор, линейно зависима.
4. Если система векторов 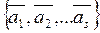
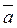
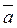
Рассмотрим систему векторов.
числа 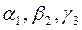
Любая лестничная система векторов линейно независимая.
Определение 5: Векторы 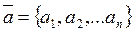
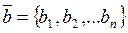
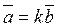
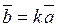
Видео:Геометрические векторы. Линейная алгебра. Лекция 1Скачать

Векторы на ЕГЭ по математике. Действия над векторами
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения 
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:
Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор 
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: 
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами:
Здесь в скобках записаны координаты вектора 
Находятся они просто: координата конца вектора минус координата его начала.
Если координаты вектора заданы, его длина находится по формуле
Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Сложение векторов
Для сложения векторов есть два способа.
1 . Правило параллелограмма. Чтобы сложить векторы 



Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы 



По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .
При сложении векторов 

Видео:Линейная алгебра. Векторы и операции над векторами.Скачать

Вычитание векторов
Вектор 



Теперь понятно, что такое вычитание векторов. Разность векторов 



Видео:Линейная зависимость и линейная независимость векторов.Скачать

Умножение вектора на число
При умножении вектора 



Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:
Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов 

Из формулы для скалярного произведения можно найти угол между векторами:
Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.
 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.
🎬 Видео
Арифметическая прогрессия 9 класс. Формулы, о которых вы не знали | МатематикаСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Как разложить вектор по базису - bezbotvyСкачать

Коллинеарность векторовСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Как за 10 минут понять СЛОЖНЕЙШУЮ ТЕМУ в Алгебре? Геометрическая прогрессияСкачать

Базис (завершение). Геометрические векторы (начало) | Лекция 4 | ЛинАл | СтримСкачать

§2 Линейная операция над векторамиСкачать


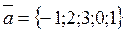
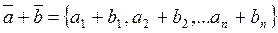
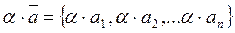
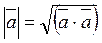
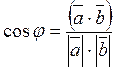
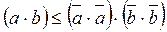
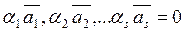

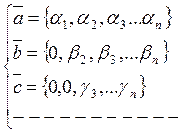

















 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»