Как изображаются окружности в аксонометрии ответ (8 видео)

Аксонометрические проекции

Согласно ГОСТ 2.317-69, из прямоугольных аксонометрических проекций рекомендуется применять прямоугольные изометрию и диметрию.

В прямоугольной изометрии размеры предмета по всем трем измерениям сокращаются на 18 %. ГОСТ рекомендует изометрическую проекцию строить без сокращения по осям координат), что соответствует увеличению изображения против оригинала в 1,22 раза.

На рисунках 172 и 173 показано расположение осей в изометрии и диметрии.

Рисунок 172 — Расположение осей в изометрии

Р исунок 173 — Расположение осей в диметрии

При построении прямоугольной диметрической проекции сокращение длин по оси y’ принимают вдвое больше, чем по двум другим. В практических построениях вводится масштаб увеличения, равный 1,06, и тогда коэффициенты искажения по осям x’ и z’ равны единице, а по оси y’ вдвое меньше — 0,5.

Содержание

Построение окружности в аксонометрии
Построение аксонометрических изображений
Штриховка в аксонометрии
Построение аксонометрических проекций окружности
Изображение окружностей на аксонометрических плоскостях
🔥 Видео

Видео:2 2 3 построение изометрии окружностиСкачать

Построение окружности в аксонометрии

При параллельном проецировании окружности на какую-нибудь плоскость П* получаем ее изображение в общем случае в виде эллипса (рисунок 174).

Рисунок 174 — Проецирование окружности на плоскость

ГОСТ 2.317-69 определяет положение окружностей, лежащих в плоскостях, параллельных плоскостям проекций для прямоугольной изометрической проекции (рисунок 175) и для прямоугольной диметрии (рисунок 177).

Рисунок 175 — Изометрические проекции окружностей расположенных в

плоскостях параллельных плоскостям проекций

Построение изометрической проекции окружности показано на рисунке 176. Если изометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1,2, 3 равна 1,22, а малая ось — 0.71 диаметра окружности. Если изометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая — 0.58 диаметра окружности.

Рисунок 176 — Построение изометрической проекции окружности

Рисунок 177 — Диметрические проекции окружностей расположенных в

плоскостях параллельных плоскостям проекций

Построение диметрической проекции окружности представлено на рисунке 178. Если диметрическую проекцию выполняют без искажения по осям x и z то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 — 0.95, эллипсов 2 и 3 — 0.35 диаметра окружности. Если диметрическую проекцию выполняют с искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 — 0.9, эллипсов 2 и 3 — 0,33 диаметра окружности.

Рисунок 178 — Построение диметрической проекции окружности

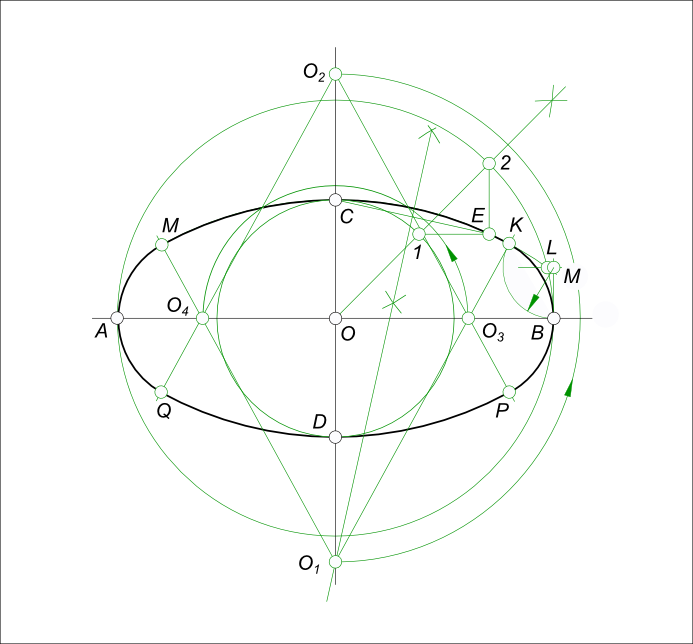
Как бы ни была расположена плоскость окружности, сначала целесообразно построить параллелограмм A*B*C*D* – параллельную проекцию квадрата ABCD, описанного около данной окружности, а затем с помощью восьми точек и восьми касательных вписать в него эллипс. Точки 1, 3, 5 и 7 – середины сторон параллелограмма. На отрезке 3*B*, как на гипотенузе, построить прямоугольный равнобедренный треугольник 3*KB*; из точки 3* радиусом 3*K описать полуокружность, которая пересечет A*B* в точках L и M; эти точки делят отрезок 3*A* и равный ему отрезок 3*B* в отношении 3:7; через точки L и М провести прямые параллельные боковым сторонам параллелограмма, и отметить точки 2*, 4*, 6* и 8* расположенные на диагоналях. Построить касательные к эллипсу в найденных точках. Касательные t₂ и t₆ параллельны BD, а касательные t₄ и t₈ параллельны AC. Получив восемь точек и столько же касательных, можно с достаточной точностью вычертить эллипс (рисунок 179).

Рисунок 179 — Построение эллипса

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Построение аксонометрических изображений

Переход от ортогональных проекций предмета к аксонометрическому изображению рекомендуется осуществлять в такой последовательности:

На ортогональном чертеже размечают оси прямоугольной системы координат, к которой и относят данный предмет. Оси ориентируют так, чтобы они допускали удобное измерение координат точек предмета. Например, при построении аксонометрии тела вращения одну из координатных осей целесообразно совместить с осью тела (рисунок 180)

Рисунок 180 — Построение аксонометрического изображения

2. Строят аксонометрические оси с таким расчетом, чтобы обеспечить наилучшую наглядность изображения и видимость тех или иных точек предмета.

3. По одной из ортогональных проекций предмета чертят вторичную проекцию.

4. Создают аксонометрическое изображение, для наглядности делают вырез четверти.

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Штриховка в аксонометрии

Согласно ГОСТ 2.317-68 ЕСКД линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (рисунок 181).

Рисунок 181 — Штриховка в аксонометрии

При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии – параллельно измеряемому отрезку.

В аксонометрических проекциях спицы маховиков и шкивов, ребра жесткости и подобные элементы штрихуют.

Видео:Построение аксонометрии моделиСкачать

Построение аксонометрических проекций окружности

Построение аксонометрических проекций окружности вызывает трудности, в связи с тем, что окружность принимает вид эллипса в аксонометрии. Возникает вопрос: как рисовать эллипс? Чтобы построить окружность в аксонометрии используют следующие способы: — построение по вспомогательной квадратной сетке; — построение при помощи циркуля;

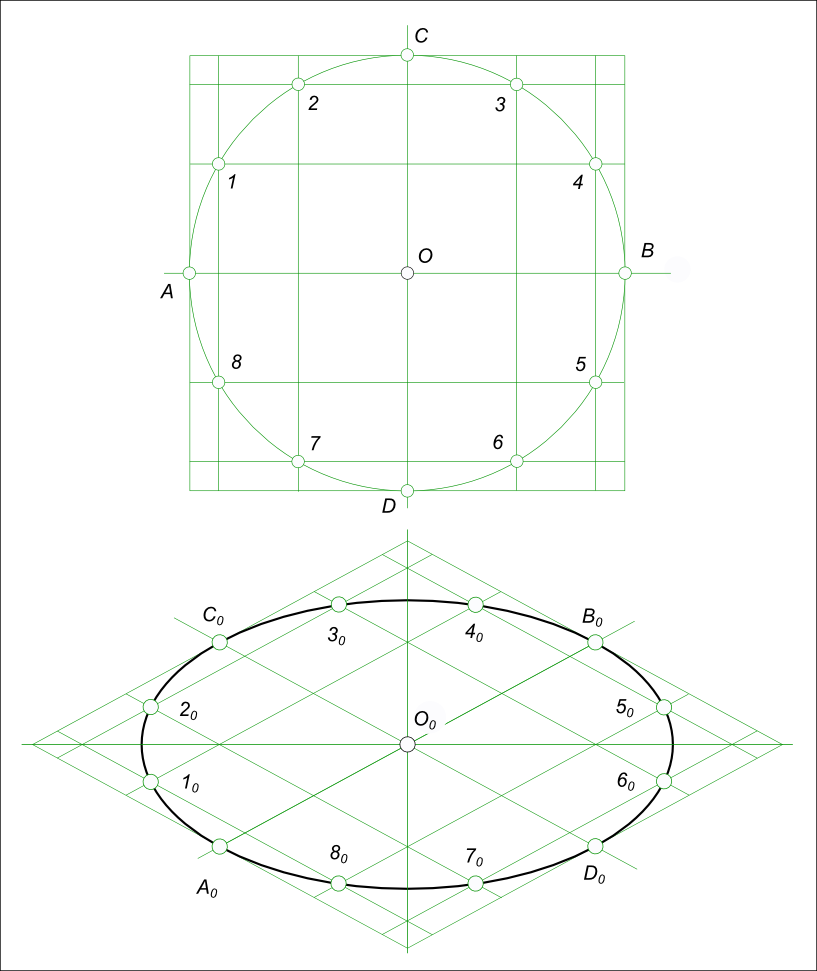
По первому способу квадрат описывает окружность и делится на 4×4=16. Отмечаем точки пересечения линий сетки с линией окружности. Затем строим аксонометрическую проекцию сетки и на ней отмечаем точки A₀, 1₀, 2₀, . 8₀. По этим точкам строим окружность, при помощи лекала. Данным способом окружность строится также в перспективе.

Окружность для данного вида аксонометрической проекции — прямоугольной изометрии получилась получилась несколько больше своего действительного размера, в следствии применения приведенных коэффициентов искажения.

По второму способу окружность строится при помощи циркуля Построение аксонометрических проекций окружности в косоугольной фронтальной диметрии

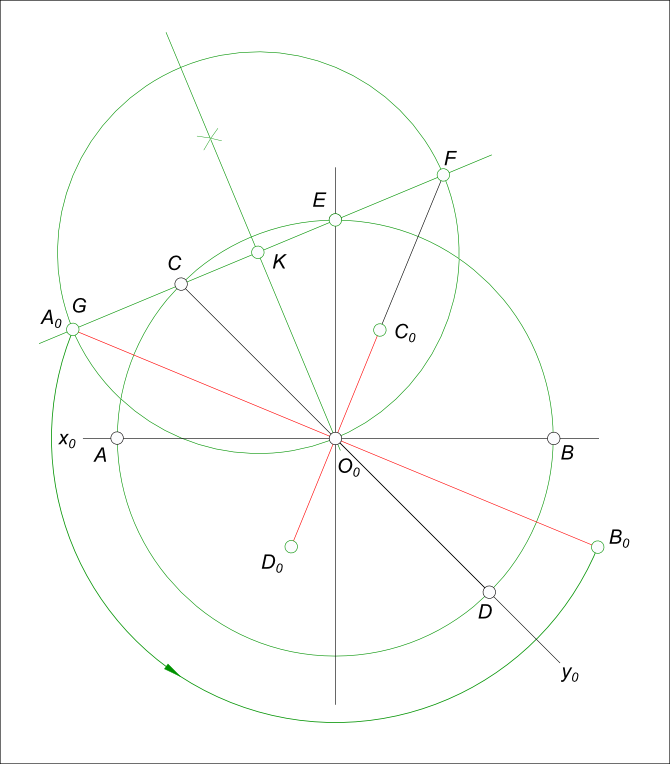
Пусть окружность расположена параллельно горизонтальной плоскости проекции: — сначала определяем направление большой и малой оси эллипса, используя для этого построение показанное на рисунке Сопрягаемые диаметры AB и CD построены на аксонометрических осях x₀ и y₀, их центры совпадают с началом координат. Концы одного из диаметров (AB) соединим дугой окружности из центра O₀. Восстановив перпендикуляр к диаметру в точке O₀ отметим на их пересечении точку E. Соединяем точки C, E прямой линией. Находим середину отрезка CE — точку K. Из точки K описываем окружность радиусом KO₀ и отмечаем точки F и G, в которых она пересекается с прямой CE. Длина половины большой оси равна отрезкам GE, CF, длина половины малой оси равна отрезкам CG, EF; — затем, после построения осей эллипса:

— проводим прямую O — 2 делящую угол между осями пополам при этом находим точки 1 и 2 пересечения данной прямой с окружностями малой и большой оси; — из точки 1 проводим прямую параллельную большой оси, а из точки 2 проводим прямую параллельную малой оси и на их пересечении находим точку эллипса E; — соединяем точки E, C прямой линией. Через середину отрезка CE восстанавливаем к нему перпендикуляр до пересечения с малой осью в точке O₁, которая определяет центр дуги CE; — строим точку O₂ симметричную O₁, относительно центра эллипса — O; — на пересечении дуг CE и 2B отмечаем точку L, проводим через данную точку прямую параллельную большой оси до пересечения ее в точке M с прямой BM, перпендикулярной большой оси — OB; — из центра M проводим дугу радиусом MB до пересечения ее с дугой CE в точке K, являющейся точкой сопряжения дуг овала; — соединив прямой линией точки K и O₁ на пересечении ее с большой осью находим точку O₃, являющуюся центром дуги BK; — точку P находим на пересечении прямой O₂O₃ с дугой радиусом O₃B. P — точка сопряжения дуг BK и BP; — точке O₃ симметрична относительно центра эллипса точка O₄; — аналогично, построив точки сопряжения для левой половины , проводим дуги овала, предварительно удалив ненужные построения.

Построение аксонометрических проекций окружности в прямоугольной изометрии

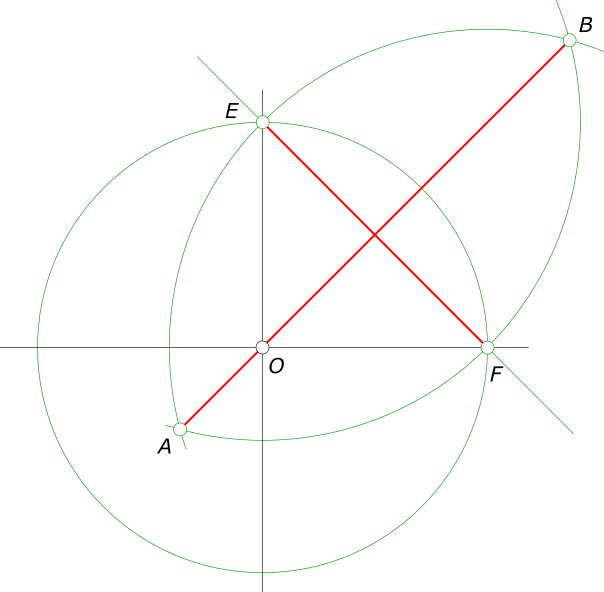
Графически определяем размеры осей эллипса: — проводим две взаимно перпендикулярные линии; — приняв точку их пересечения за центр O, описываем из него окружность заданного диаметра и отмечаем точки E и F; — из точек E и F описываем дуги радиусом R = EF = FE и находим точки их пересечения A и B; — соединив точки A и B, получим большую ось эллипса, равную 1,22d; — соединив точки E и F, получим малую ось эллипса, равную 0,7d

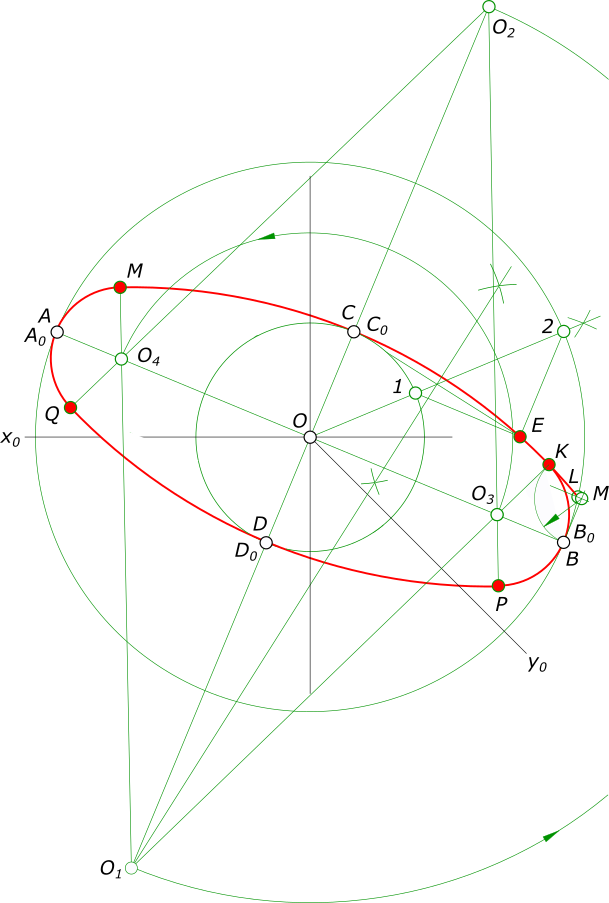
Пусть, строится окружность, расположенная параллельно горизонтальной плоскости проекции

где большая ось AB перпендикулярна свободной оси (z) и малая ось CD. — затем, после построения осей эллипса: — проводим прямую O — 2 делящую угол между осями пополам при этом находим точки 1 и 2 пересечения данной прямой с окружностями малой и большой оси; — из точки 1 проводим прямую параллельную большой оси, а из точки 2 проводим прямую параллельную малой оси и на их пересечении находим точку эллипса E; — соединяем точки E, C прямой линией. Через середину отрезка CE восстанавливаем к нему перпендикуляр до пересечения с малой осью в точке O₁, которая определяет центр дуги CE; — строим точку O₂ симметричную O₁, относительно центра эллипса — O; — на пересечении дуг CE и 2B отмечаем точку L, проводим через данную точку прямую параллельную большой оси до пересечения ее в точке M с прямой BM, перпендикулярной большой оси — OB; — из центра M проводим дугу радиусом MB до пересечения ее с дугой CE в точке K, являющейся точкой сопряжения дуг овала; — соединив прямой линией точки K и O₁ на пересечении ее с большой осью находим точку O₃, являющуюся центром дуги BK; — точку P находим на пересечении прямой O₂O₃ с дугой радиусом O₃B. P — точка сопряжения дуг QP и BP; — точке O₃ симметрична относительно центра эллипса точка O₄; — аналогично, построив точки сопряжения для левой половины , проводим дуги овала, предварительно удалив ненужные построения.

Более просто выглядит построение окружности, расположенной параллельно горизонтальной плоскости проекции

Видео:Окружность в прямоугольной изометрии 3 способ построенияСкачать

Изображение окружностей на аксонометрических плоскостях

В прямоугольной изометрической проекции окружности, расположенные в плоскостях, параллельных плоскостям П₁, П₂, П₃, изображаются эллипсами. Они строятся по большой и малой осям, которые равны 1,22d и 0,77d или заменяются овалами. Построение эллипсов представлено на рис. 5.3. В прямоугольной диметрической проекции окружность, расположенная во фронтальной плоскости , проецируется в эллипс с осями, равными 1,06d и 0,94d. Окружности, расположенные в горизонтальной и профильной плоскостях, проецируются в одинаковые эллипсы с осями, равными 1,06d и 0,35d. Построение эллипсов в диметрии представлено на рис. 5.3. Построение эллипсов в аксонометрии часто заменяется построением четырехцентровых овалов, представленные на рис. 5.4.

Рис.5.4

Построение эллипса по восьми точкам.Построение эллипса по восьми точкам начинаем с построение большой оси, всегда расположенной перпендикулярно отсутствующей в плоскости оси( отрезок 1-2). Малая соь эллипса располагается перпендикулярно большой оси эллипса и, следовательно, совпадает с отсутствующей в плоскости осью ( отрезок 3-4-).

Церез центр эллипса проводятся аксонометрические оси, находящиеся в данной плоскости и на них откладываются отрезки равные диаметру окружности отрезки, которую строят в изометрии ( отрезок 7 – 8)и во фронтальной плоскости для диметрии ( отрезки 5 – 6). В горизонтальной и профильной плоскости для диметрии вдоль оси Y откладывается отрезок равный 0,5d ( отрезок 7 – 8)

При построении наглядных изображений на практике используют чаще всего аксонометрические проекции, приведенные в ГОСТе 2.317-69*.

При выборе вида аксонометрических изображений следует руководствоваться такими рекомендациями:

1. Изометрическую проекцию следует применять тогда, когда все три стороны объекта имеют приблизительно одинаковое количество особенностей;

2. Прямоугольную диметрическую проекцию применяют в случаях, когда только одна сторона объекта содержит наибольшее количество особенностей;

3. Косоугольную диметрическую проекцию применяют тогда, когда объект имеет ряд окружностей, расположенных в плоскостях параллельных П₂.

Из прямоугольных аксонометрических проекций лучше выбирать диметрическую проекцию или прямоугольную изометрию. Прямоугольная изометрическая проекция проще в построении, так как при этом коэффициенты искажения по всем осям равны между собой и равны:

Для упрощения построения объектов в изометрии коэффициенты искажения округляются до 1 , но изображение при этом получается увеличенным. Для прямоугольной диметрии выбираются коэффициенты искажения равными:

Для упрощения вычисления размеров при построении диметрической проекции объекта коэффициенты искажения округляются и принимаются равными:

Для построения объекта в аксонометрии необходимо сначала построить его проекционный чертеж, а затем используется способ координат. В этом случае аксонометрические проекции объекта строятся по координатам отдельных точек, взятым с ортогонального чертежа. Построение , как правило , начинается с построения вторичной проекций точек. В качестве вторичной проекции чаще всего используем горизонтальную проекцию точки. Затем из горизонтальной вторичной проекции проводим прямую, параллельную оси Z ( строго вертикальную прямую). На ней откладываем координату Z точки и получаем первичную проекцию, т.е.ее аксонометрическую изображение( рис. 5.5).

Вторичная проекция

Рис. 5.5

При построении прямоугольной изометрической проекции шестигранной призмы используем ортогональный чертеж призмы шестиугольника ( рис. 5.6). За оси координат принимаем оси симметрии. Затем проводим аксонометрические оси. Далее от начала координат откладываем вершины шестиугольника вдоль оси Х , находим остальные вершины на отрезках параллельных оси Y. Построив нижнее основание призмы откладываем высоту призмы и строим параллельное верхнее основание.

Используя ортогональный чертеж пирамиды и задавшись видом аксонометрии, строим ее аксонометрическое изображение( рис. 5.6).

Рис. 5.6

Последовательность изображения детали в аксонометрии представлена на рис. 5.7. Сначала на ортогональном чертеже детали выполняем разрезы и определяем положение координатных осей. При изображении аксонометрии симметричных тел целесообразно одну из осей ( в данном случае ось Z) совместить с осью тела.

Первым этапом построения аксонометрической проекции детали проводим аксонометрические оси и делаем разметку всех центров отверстий, отмечая их аксонометрическими осями.

Второй этап состоит в изображений фигур сечений, получаемых при мысленном рассечении тела плоскостями параллельными П₁, П₂, П₃. Выполняем штриховку сечений соответственно направлениям представленным на рис. 5.7. В прямоугольной диметрии коэффициент искажения по оси Y равен 0,5 и штриховка выполняется с учетом этого. Следует отметить, что условность , применяемая на чертежах по ГОСТ 2.305-68 относительно сплошных тонких тел, называемых ребрами жесткости, круглых непустотелых валов и т.п., на аксонометрические проекции не распространяются. Эти элементы в аксонометрии показываются рассеченными и заштриховываются.

Третий этапсостоит в построении линий пересеения поверхностей тела, лежащих за секущими плоскостями.

Четвертый этапдополняет построение поверхностей деталей, лежащих за фигурами сечений.

Пятый этап завершаем построение аксонометрического изображения детали , выполняя его обводку сплошной основной линией по ГОСТ 2.303-68, толщиной от 0,6 до 1,5 мм.