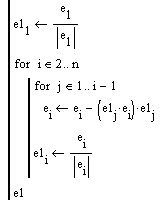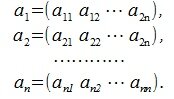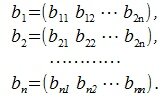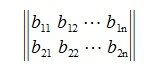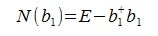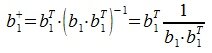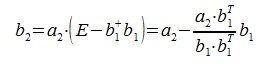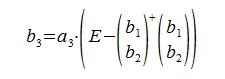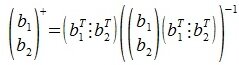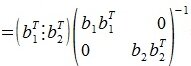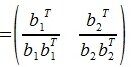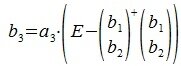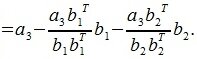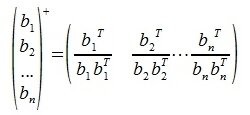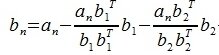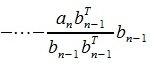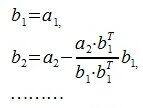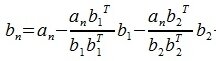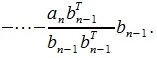| Классическая ортогонализация Грама-Шмидта | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(N^3)[/math] |
| Объём входных данных | [math]N^2[/math] |
| Объём выходных данных | [math]3N^2/2[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(N^2)[/math] |
| Ширина ярусно-параллельной формы | [math]O(N)[/math] |
Основные авторы описания: Инжелевская Дарья Валерьевна (свойства и структура алгоритмов), А.В.Фролов(общая редактура текста)
- Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.5.1 Пример реализации на Python
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- Процесс ортогонализации Грама-Шмидта
- Примеры решения задач
- Ортогональная матрица. Ортогонализация Грамма-Шмидта.
- Ортогонализация Грамма-Шмидта
- Ортонормализация Грамма-Шмидта
- 🔥 Видео
Видео:A.7.4 Ортогонализация набора векторов. Процесс Грама-Шмидта.Скачать

Содержание
Видео:Процесс ортогонализации Грама-Шмидта. ПримерСкачать

1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
1.2 Математическое описание алгоритма
Пусть имеются линейно независимые векторы [math]mathbf_1,;ldots,;mathbf_N[/math] .
то классический процесс Грама — Шмидта выполняется следующим образом:
На основе каждого вектора [math]mathbf_j ;(j = 1 ldots N)[/math] может быть получен нормированный вектор: [math]mathbf_j = <mathbf_jover | mathbf_j |_2>[/math] (у нормированного вектора направление будет таким же, как у исходного, а длина — единичной).
Результаты процесса Грама — Шмидта:
[math]mathbf_1,;ldots,;mathbf_N[/math] — система ортогональных векторов либо
[math]mathbf_1,;ldots,;mathbf_N[/math] — система ортонормированных векторов.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро последовательной версии метода ортогонализации Грамма-Шмидта можно составить из множественных (всего их [math]frac[/math] ) вычислений проекций : [math]mathbf_<mathbf>,mathbf[/math]
1.4 Макроструктура алгоритма
Данный алгоритм использует в качестве составных частей другие, более мелкие. Далее описание будет не в максимально детализированном виде (т.е. на уровне арифметических операций), а только на уровне его макроструктуры. Типичной макрооперацией, часто встречающиеся в алгоритме является оператор проекции векторов. Как записано и в описании ядра алгоритма, основную часть метода ортогонализации Грамма-Шмидта составляют множественные (всего их [math]frac[/math] ) вычисления оператора проекции.
1.5 Схема реализации последовательного алгоритма
Следующий алгоритм реализует нормализацию Грамма-Шмидта. Векторы [math]v_1. v_k[/math] заменяются набором ортонормированных векторов, которые имеют ту же линейную оболочку.
Вычислительная сложность этого [math]2Nk^2[/math] операции с плавающей точкой, где N — размерность векторов.
Последовательность исполнения метода следующая:
1.5.1 Пример реализации на Python
1.6 Последовательная сложность алгоритма
Для построения ортогонального набора векторов в последовательном варианте требуется:
При классификации по последовательной сложности, таким образом, ортогонализация Грамма-Шмидта относится к алгоритмам с кубической сложностью.
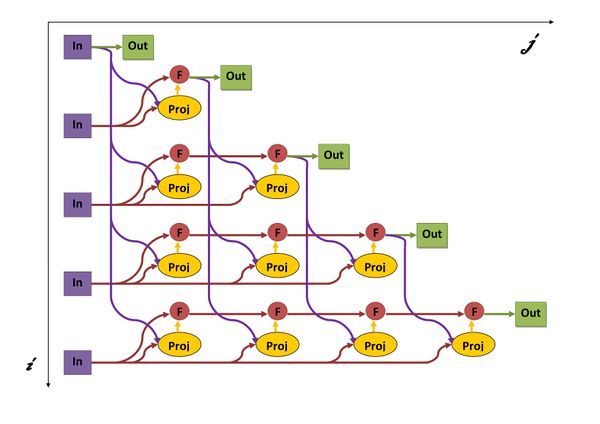
1.7 Информационный граф
Опишем граф алгоритма как аналитически, так и в виде рисунка.
Граф алгоритма состоит из двух групп вершин, расположенных в целочисленных узлах двух областей.
Первая группа вершин расположена в двумерной области, соответствующая ей операция [math]mathbf_<mathbf>,mathbf = <langle mathbf, mathbf rangle over langle mathbf, mathbfrangle> mathbf ,[/math] .
Естественно введённые координаты области таковы:
i — меняется в диапазоне от 2 до N, принимая все целочисленные значения;
j — меняется в диапазоне от 1 до i-1, принимая все целочисленные значения.
Аргументы операции следующие:
[math]a_i[/math] : элементы входных данных, а именно [math]a_i[/math] ;
[math]b_j[/math] : результат срабатывания операции, соответствующей вершине из второй группы, с координатой j.
Вторая группа вершин расположена в двухмерной области, соответствующая ей операция [math]a — b[/math] .
Естественно введённые координаты области таковы:
i — меняется в диапазоне от 2 до N, принимая все целочисленные значения;
j — меняется в диапазоне от 1 до i-1, принимая все целочисленные значения.
Аргументы операции следующие:
j=1 — входные данные [math]a_j[/math]
j>1 — результат срабатывания операции, соответствующей вершине из второй группы, с координатой j-1
результат срабатывания операции, соответствующей вершине из первой группы, с координатой j
1.8 Ресурс параллелизма алгоритма
В параллельном варианте, в отличие от последовательного, можно параллельно производить вычитание соответствующего [math]mathbf_<mathbf>,mathbf[/math] для всех [math]i=j+1..N[/math] . Параллельное же вычисление проекций соответствует другому алгоритму.
При классификации по высоте (количество ярусов в ЯПФ ) ЯПФ, таким образом, ортогонализация Грамма-Шмидта относится к алгоритмам со сложностью [math]O(N^2)[/math] .
При классификации по ширине (максимальное количество вершин в ярусе) ЯПФ его сложность будет [math]O(N)[/math] .
1.9 Входные и выходные данные алгоритма
Объём входных данных: [math]Nk[/math]
Выходные данные: множество ортогональных векторов [math] <displaystyle mathbf _,;ldots ,;mathbf _> [/math] , каждый из которых описывается [math]mathbf[/math] .
Объём выходных данных: [math]Nk[/math]
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным (отношение кубической к квадратичной).
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, также линейна.
Алгоритм почти полностью детерминирован — единственность результата выполнения гарантирована, однако возможно накопление ошибок округления при использовании классического процесса Грама-Шмидта.
Алгоритм является численно неустойчивым — ошибки округления могут привести к неортогональности полученных векторов.
Процесс Грама — Шмидта может применяться также к бесконечной последовательности линейно независимых векторов.
Процесс Грама ― Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольной матрицы с положительными диагональными элементами ― QR-разложение, что есть частный случай разложения Ивасавы.
Видео:Лекция 5.7. Ортогонализация Грама-Шмидта: примерСкачать

Процесс ортогонализации Грама-Шмидта
Определение. Векторы $a$ и $b$ называются ортогональными, если их скалярное произведение равно нулю.$$left(a, bright)=0.$$
Определение. Системы $S_ = langle a_,a_,…,a_rangle,$ и $S_ = langle b_,b_,…,b_rangle,$ называются эквивалентными, когда векторы каждой из систем, линейно выражаются через векторы, другой системы.
Теорема. Допустим, у нас есть линейно независимая система $S = langle a_,a_,ldots,a_rangle.$ Тогда всегда найдется такая система $S_ = langle b_,b_,…,b_rangle,$ которая будет эквивалентной и ортогональной к $S,$ которая получается следующим методом:
Докажем же существование $S_$ эквивалентной $S$ с помощью индукции. При $k = 1$ $$b_ = a_.$$ При $k = 2$ $$left(b_, b_right) = left(a_ + lambda_b_, b_right) = left(a_, b_right) + lambda_left(b_, b_right) =$$$$= left(a_, b_right)-dfrac<left(a_, b_right)><left(b_, b_right)>left(b_, b_right) = 0.$$ Из чего очевидно, что $S = langle a_,a_rangle$ и $S_ = langle b_,b_rangle$ — эквивалентны.
Теперь докажем для $k = m,$ при $2leqslant jleqslant k$ $$left(b_, b_right) = left(a_ + sumlimits_^lambda_b_, b_right) = left(a_, b_right) + sumlimits_^lambda_left(b_, b_right) =$$$$= left(a_, b_right)-sumlimits_^dfrac<left(a_, b_right)><left(b_, b_right)>left(b_, b_right) = 0.$$ Как видим, по индукции мы доказали, что любой ЛНЗ системе, методом Грама-Шмидта, можно найти эквивалентную ей ортогональную систему.
Видео:Процесс ортогонализации Грама-Шмидта. ТемаСкачать

Примеры решения задач
Рассмотрим примеры задач, в которых может использоваться процесс ортогонализации Грама-Шмидта. Постарайтесь решить данные примеры самостоятельно, а затем сверить свое решение с приведенным.
- Применяя процесс ортогонализации по Грамму-Шмидту построить ортогональный базис подпространства, натянутого на данную систему векторов $S = langle a_, a_, a_rangle.$
$$a_ = (1, 2, 2, -1), a_ = (1, 1, -5, 3), a_ = (3, 2, 8, -7).$$
Первым делом, найдем $b_$. В первом пункте пишется, что $b_ = a_.$
Дальше найдем $b_.$ Из формулы пункта 2), мы видим, что: $$b_ = a_ + lambda_ cdot b_, lambda_ = dfrac<left(a_, b_right)><left(b_, b_right)>,$$ все необходимое для решения мы нашли, осталось только решить. Итак:$$lambda_ = -dfrac<left(a_, b_right)><left(b_, b_right)> = -dfrac = -left(dfracright) = 1,$$ лямбду мы нашли, $b_$ у нас есть, теперь мы можем найти $b_:$ $$b_ = a_ + lambda_cdot b_ = (1, 1, -5, 3) + (1, 2, 2, -1) = (2, 3, -3, 2).$$
Выпишем же формулу для $b_:$ $$b_ = a_ + lambda_ cdot b_ + lambda_ cdot b_,$$ при $$lambda_ = -dfrac<left(a_, b_right)><left(b_, b_right)>,quad lambda_ = -dfrac<left(a_, b_right)><left(b_, b_right)>,$$ найдем все необходимое: $$lambda_ = -dfrac= -3,$$ $$lambda_ = -dfrac= 1.$$ Теперь вычислим $b_:$ $$b_ = (3, 2, 8, -7)-3(1, 2, 2, -1) + 1(2, 3, -3, 2) = (2, -1, -1, 2).$$
Получили ортогональный базис $S_ = langle b_, b_, b_rangle$ — систему, эквивалентную данной, $S = langle a_, a_, a_rangle.$ $$S_ = langle (1, 2, 2, -1), (2, 3, -3, 2), (2, -1, -1, 2)rangle.$$
Применяя процесс ортогонализации по Грамму-Шмидту построить ортогональный базис подпространства, натянутого на данную систему векторов $S = langle a_, a_, a_rangle.$
$$a_ = (1, 1, -1, -2), a_ = (5, 8, -2, -3), a_ = (3, 9, 3, 8).$$
Первым делом, найдем $b_$, $b_ = a_.$
Дальше найдем $b_.$ Из формулы пункта 2) мы видим, что: $$b_ = a_ + lambda_ cdot b_, lambda_ = dfrac<left(a_, b_right)><left(b_, b_right)>,$$ все необходимое для решения мы нашли, осталось только решить. Итак:$$lambda_ = -dfrac = -left(dfracright) = 3,$$ лямбду мы нашли, $b_$ у нас есть, теперь мы можем найти $b_:$ $$b_ = a_ + lambda_cdot b_ = (5, 8, -2, -3) + (-3, -3, 3, 6) = (2, 5, 1, 3).$$
Видео:Ортогональные системы векторов. Процесс ортогонализации (задача 1357)Скачать

Ортогональная матрица. Ортогонализация Грамма-Шмидта.
Квадратная матрица 
где E — единичная матрица, A T — транспонированная матрица.
Из условия AA T =E следует, что A T является обратной к матрице A:
Для любой невырожденной квадратной матрицы можно построить ортогональную матрицу. Для построения ортогональной матрицы применяют метод ортогонализации Грамма-Шмидта. Затем нормируют полученные векторы строки. Эти две процедуры вместе называют методом ортонормализации Грамма-Шмидта.
Видео:Лекция 5.8. Ортогонализация Грама-ШмидтаСкачать

Ортогонализация Грамма-Шмидта
Пусть задана некоторая квадратная матрица, строки которой являются векторы
и пусть эти векторы линейно независимы (т.е. матрица построенная этими векторами строками невырождена). Требуется получить взаимно ортогональные n векторы
Суть метода заключается в следующем:
1. Выбирается некоторая строка (пусть это будет a1). b1 выбирается равным a1.
3. Вектор b3 получается проектированием a3 на нуль-пространство матрицы
Рассмотрим подробнее процесс ортогонализации.
На втором шаге вычисляем нуль-пространство b1:
где E- единичная матрица порядка nxn,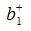
Для пректирования a 2 на нуль-пространство b 1 вычисляем
На третьем шаге вычисляем b 3:
Так как векторы b 1 и b 2 ортогональны, то
Для n -го вектора получим:
Таким образом, процедура ортогонализации Грамма-Шмидта имеет следующий вид:
Видео:Практика 19 Процесс ортогонализации Грама ШмидтаСкачать

Ортонормализация Грамма-Шмидта
Суть метода ортонормализации Грамма-Шмидта заключается в ортогонализации методом Грамма-Шмидта а затем нормализации полученных векторов строк:
🔥 Видео
Ортогонализация Грама Шмидта 1361Скачать

Процесс ортогонализации Грама-Шмидта. Еще один примерСкачать

Линейная алгебра Практика 16 Процесс ортогонализации Грама Шмидта Ортогональный оператор ПриведеСкачать

Процесс ортогонализации Грама-Шмидта. ОтветыСкачать

Метод ортогонализации Грама-Шмидта. Семинар 24Скачать
10 5 Процесс ортогонализацииСкачать

Ортогонализация Грама-Шмидта, ортонормированный базис | 27 | Константин Правдин | ИТМОСкачать

Матрица ГрамаСкачать

10. Ортогонализация с помощью процедуры Грама ШмидтаСкачать
Процесс ортогонализации Грама-Шмидта. ВопросыСкачать
Линейная алгебра | ортогонализация по Граму Шмидту | 1Скачать

Скалярное произведение. Ортогональный базис.Скачать

Тимашев Д.А. - Линейная алгебра и геометрия. Лекции - 15. Ортогонализация Грама–ШмидтаСкачать