Abcda1b1c1d1 прямоугольный параллелепипед какая из прямых параллельна плоскости a1ad ответ

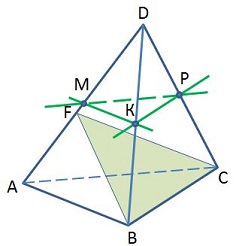
Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FАB.

Комментарий:
1) МК – средняя линия треугольника ADB, следовательно МК || АВ.
2) АВ лежит в плоскости FАB, следовательно по признаку параллельности прямой и плоскости МК || FАВ

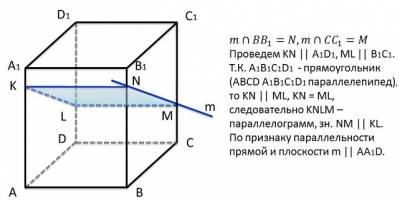
АВСDA ₁ B₁ C₁ D₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A₁ AD?

Комментарий:

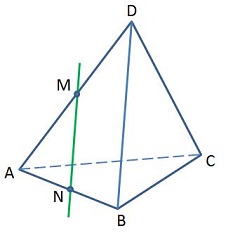
В тетраэдре DАВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN?

Комментарий:
MN – средняяя линия треугольника ADB, значит MN || DB. По признаку параллельности прямой и плоскости MN || DBC.

Выберите ВЕРНЫЕ высказывания:

1Параллельные прямые не имеют общих точек.2Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости.3Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей.4Существует параллелепипед, у которого все углы граней острые

Комментарий
«Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.»
Высказывание № 1 – верно. «не пересекаются», значит не имеют общих точек
Высказывание № 2 – неверно. не каждая прямая, лежащая в параллельной для данной прямой плоскости, так же будет лежать в одной плоскости с этой прямой.
Высказывание № 3 – верно. Линия пересечения плоскостей – это прямая, принадлежащая каждой из этих плоскостей, следовательно данная прямая параллельна данным плоскостям по признаку параллельности прямой и плоскости.
Высказывание № 4 – не верно. грани параллелепипеда – параллелограммы, противоположные стороны каждого из которых параллельны, следовательно углы при них и секущей (смежная сторона) в сумме равны 180 0
Если все углы граней будут острыми, то сумма одностосронних углов будет меньше 180 0 . Получили противоречие.

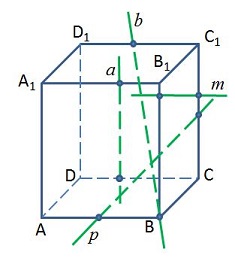
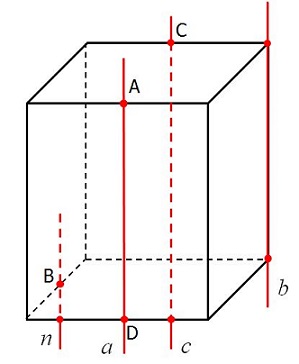
Точки А, В, С и D – середины ребер прямоугольного параллелепипеда. Назовите параллельные прямые.

1a || n2a || b3b || c4a || c

Комментарий
a || b, т.к. каждая из этих прямых параллельна одному и тому же ребру параллелепипеда – линии пересечения плоскостей, в которых лежат данные прямые.

Прямоугольный параллелепипед (продолжение)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный урок предназначен для самостоятельного ознакомления с темой «Прямоугольный параллелепипед (продолжение)». На этом занятии мы продолжим изучать прямоугольный параллелепипед. Вначале повторим основные свойства этой геометрической фигуры, затем решим несколько задач с использованием этих свойств.

Тестовые задания по геометрии к разделу «Прямые и плоскости в пространстве» 1 курс СПО

Тестовые задания по геометрии к разделу «Прямые и плоскости в пространстве»1.Аксиомы стереометрии. 2.Параллельность прямых и плоскостей. 3.Перпендикулярность прямых и плоскостей. Ответы в конце разработки

Просмотр содержимого документа
«Тестовые задания по геометрии к разделу «Прямые и плоскости в пространстве» 1 курс СПО»

Прямые и плоскости в пространстве

Предмет стереометрии. Основные понятия и аксиомы стереометрии.

Параллельность прямыхв пространстве. Параллельность двух плоскостей.

Векторы в пространстве.

Перпендикулярность прямых, прямой и плоскости.

Перпендикуляр и наклонная.

Угол между прямой и плоскостью.

Двугранный угол. Перпендикулярность плоскостей.

Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.

1) АВС 2) DBC 3) DAB 4) DAC

Каким плоскостям принадлежит точка К?

Выберите верные высказывания:

1) Любые три точки лежат в одной плоскости.

2) Если центр окружности и ее точка лежат в плоскости, то и вся окружность лежит в этой плоскости.

3) Через три точки, лежащих на прямой, проходит только одна плоскость.

4) Через две пересекающихся прямые проходит плоскость , и притом только одна.

Выберите неверные высказывания:

1) Если три прямые имеют общую точку, то они лежат в одной плоскости.

2) Прямая, пересекающая две стороны треугольника, лежит в плоскости этого треугольника.

3) Две плоскости могут имеет только две общие точки.

4) Три попарно пересекающиеся в разных точках прямые, лежат в одной плоскости.

Назовите прямую, по которой пересекаются плоскости A₁BC и A₁AD.

Назовите прямую, по которой пересекаются плоскости DCC₁ и A₁AD.

Прямые АВ и CD пересекаются. Через прямую АВ проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью ВСD.

1) АС 2) АB 3) BС 4) ВD

Прямые АВ и CD пересекаются. Через точки В и D проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью AСD.

1) АС 2) АB 3) BС 4) ВD

Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.

1) АВС 2) DBC 3) DAB 4) DAC

Каким плоскостям принадлежит точка F?

Выберите верные высказывания:

1) Любые четыре точки лежат в одной плоскости.

2) Через прямую и не лежащую на ней точку проходит только одна плоскость.

3) Если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости .

4) Две плоскости могут иметь только одну общую точку.

Выберите неверные высказывания:

1) Две окружности, имеющие общий центр, лежат в одной плоскости .

2) Прямая, проходящая через вершину треугольника, лежит в плоскости этого треугольника.

3) Три вершины треугольника принадлежат одной плоскости.

4) Через две параллельные прямые проходит плоскость , и притом только одна.

Назовите прямую, по которой пересекаются плоскости DCC₁ и A₁BC.

Назовите прямую, по которой пересекаются плоскости ABC и C₁CB.

Прямые АВ и CD пересекаются. Через прямую CD проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью AВС.

1) СD 2) АD 3) BС 4) ВD

Прямые АВ и CD пересекаются. Через точки A и D проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью BСD.

1) АС 2) АD 3) BС 4) ВD

Параллельность прямых и плоскостей

Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FBC.

1) МР 2) РК 3) МК 4) МК и РК

АВСDA₁B₁C₁D₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A₁B₁C₁?

В тетраэдре DАВС ВК = КС, DP = PC. Плоскости какой грани параллельна прямая РК?

1) DAB 2) DBC 3) DAC 4) ABC

Выберите верные высказывания:

1) Две прямые в пространстве называются параллельными, если они не пересекаются.

2) Если одна из двух параллельных прямых параллельна плоскости, то другая прямая либо так же ей параллельна, либо лежит в этой плоскости.

3) Существует такая прямая, которая лежит в плоскости и параллельна прямой, пересекающей данную плоскость.

4) Скрещивающиеся прямые не имеют общих точек.

Точки А, В, С и D – середины ребер прямоугольного

параллелепипеда. Назовите параллельные прямые.

Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания:

1) Прямые СD и MN скрещивающиеся.

2) Прямые АВ и MN лежат в одной плоскости.

3) Прямые СD и MN пересекаются.

4) Прямые АВ и СD скрещивающиеся.

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Треугольники АВК и АВF расположены так, что прямые АВ и FK скрещиваются. Как расположены прямые АК и ВF?

1) они параллельны 2) скрещиваются 3) пересекаются

В тетраэдре DАВС АВ = ВС = АС = 20; DA = DB = DC = 40. Через середину ребра АС плоскость, параллельная АD и ВC. Найдите периметр сечения.

Параллельность прямых и плоскостей

Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FАB.

1) МР 2) РК 3) МК 4) МК и РК

АВСDA₁B₁C₁D₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A₁AD?

В тетраэдре DАВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN?

1) DAB 2) DBC 3) DAC 4) ABC

Выберите верные высказывания:

1) Параллельные прямые не имеют общих точек.

2) Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости.

3) Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей.

4) Существует параллелепипед, у которого все углы граней острые.

Точки А, В, С и D – середины ребер прямоугольного

параллелепипеда. Назовите параллельные прямые.

Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания:

1) Прямые СD и MN пересекаются.

2) Прямые АВ и MN скрещивающиеся

3) Прямые АВ и СD параллельные.

4) Прямые АВ и MN пересекаются

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Точки А и В – середины ребер параллелепипеда. Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Два равнобедренных треугольника АВС и АВD с общим основанием АВ расположены так, что точка С не лежит в плоскости АВD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам ВС и ВD.

1) они параллельны 2) скрещиваются 3) пересекаются

В тетраэдре DАВС АВ = ВС = АС = 10; DA = DB = DC = 20. Через середину ребра ВС плоскость, параллельная АС и ВD. Найдите периметр сечения.

Перпендикулярность прямых и плоскостей

Через сторону АВ треугольника АВС проведена плоскость, перпендикулярная к стороне ВС. Определите вид треугольника относительно углов.

1) остроугольный 2) прямоугольный 3) тупоугольный

Треугольник АВС – правильный, О – центр треугольника. Расстояние от точки М до вершины А равно 3. Найдите высоту треугольника.

АВСD – параллелограмм; Найдите периметр параллелограмма.

1) 20 2) 25 3) 40 4) 60

Через вершину А треугольника ABC проведена плос­кость α, параллельная ВС. Расстояние от ВС до плоскости α равно 12. Найдите расстояние от точки пересечения ме­диан треугольника АВС до этой плоскости.

1) 8 2) 6 3) 12 4) 18

Высота ромба равна 12. Точка М равноудалена от всех сторон ромба и находится на расстоянии, равном 8, от его плоскости. Чему равно расстояние точки М до сторон ромба?

На рисунке Найдите угол между МС и плоскостью АМВ.

1) 30 0 2) 60 0 3) 90 0 4) 45 0

Выберите верные высказывания:

1) Прямая пересекает параллельные плоскости под разными углами.

2) Две прямые, перпендикулярные к одной плоскости, параллельны.

3) Длина перпендикуляра меньше длины наклонной, проведенной из той же точки.

4) Две скрещивающиеся прямые могут быть перпендикулярными к одной плоскости.

Отрезок АВ упирается концами А и В в грани прямого двугранного угла. Расстояния от точек А и В до ребра равны 1, а длина отрезка АВ равна 3. Найдите длину про­екции этого отрезка на ребро.

В тетраэдре DABC АО пресекает ВС в точке Е; Найдите .

Прямоугольник ABCD и параллелограмм ВЕМС распо­ложены так, что их плоскости взаимно перпендикулярны. Найдите угол MCD.

1) 90 0 2) 60 0 3) 30 0 4) 45 0

Перпендикулярность прямых и плоскостей

Через сторону АD параллелограмма АВСD, проведена плоскость, перпендикулярная к стороне DС. Определите вид треугольника АВС.

1) остроугольный 2) прямоугольный 3) тупоугольный

Треугольник АВС – правильный, О – центр треугольника. Высота треугольника равна 3. Найдите расстояние от точки М до вершин треугольника.

АВСD – параллелограмм; Найдите BD.

1) 20 2) 15 3) 40 4) 10

Через вершину А треугольника ABC проведена плос­кость α, параллельная ВС. Расстояние от точки пересече­ния медиан треугольника АВС до этой плоскости равно 4. На каком расстоянии от плоскости находится ВС?

1) 8 2) 6 3) 12 4) 14

Точка Р удалена от всех сторон ромба на расстояние» равное , и находится от его плоскости на расстоянии равном 2. Чему равна сторона ромба, если его угол 30°?

На рисунке Найдите угол между МС и плоскостью АМВ.

1) 30 0 2) 60 0 3) 90 0 4) 45 0

Выберите верные высказывания:

1) Угол между прямой и плоскостью может быть не больше 90 0 .

2) Две плоскости, перпендикулярные к одной прямой, пересекаются.

3) Длина перпендикуляра больше длины наклонной, проведенной из той же точки.

4) Диагональ прямоугольного параллелепипеда больше любого из ребер.

Отрезок АВ упирается концами А и В в грани прямого двугранного угла. Расстояния от точек А и В до ребра равны 2, а длина отрезка АВ равна 4. Найдите длину про­екции этого отрезка на ребро.

В тетраэдре DABC основание ABC — правильный тре­угольник. Вершина D проецируется в его центр О. Найди­те угол между плоскостью ADO и гранью DCB.

1) 30 0 2) 60 0 3) 90 0 4) 45 0

Треугольник АМВ и прямоугольник ABCD расположе­ны так, что их плоскости взаимно перпендикулярны. Най­дите угол MAD.

🔍 Видео