Видео:Угол между векторами | МатематикаСкачать

Определение взаимного угла в Matlab/Simulink
В процессе моделировании переходных процессов в Matlab/Simulink (с библиотекой SimPowerSystems) возникает необходимость в определении взаимного угла между двумя наблюдаемыми векторами (например, угол между током и напряжением или угол между двумя напряжениями). Следует отметить, что взаимным углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения второго вектора.
В статье представлены два способа моделирования отдельных пользовательских блок-элементов расчетной схемы для определения взаимного угла между двумя наблюдаемыми аналоговыми сигналами.
Рис.1. Взаимный угол между векторами
Способ №1. Определение взаимного угла из разности значений собственных углов векторов
Самым простым способом определить взаимный угол между двумя векторами является метод основанный на вычислении разности значений собственного угла первого и второго вектора:
где 
В случае если полученное значение взаимного угла отрицательное 

Следует отметить, что полученный угол имеет область значений, которая ограничивается «плавающим» интервалом 


Если 

Если 

Описанный выше алгоритм легко реализуется в программном обеспечении Matlab/Simulink.
Рис.2. Реализация в программном обеспечении Matlab/Simulink
Для преобразования аналогового сигнала в вектор используется блок «Fourier», который из периодического сигнала определяет амплитуду и фазу. В качестве блока, который позволяет выбрать необходимое значение взаимного угла используется ключ «Switch» на вход которого поступает логический сигнал «0» или «1». В зависимости от поступающего логического сигнала выбирается одно из двух значений взаимного угла.
В результате получена первая модель определения взаимного угла между аналоговыми сигналами в Matlab/Simulink область значений которой определена на интервале 
Способ №2 Определение взаимного угла из выражения для определения скалярного произведения векторов
Рассмотрим более сложный способ определения взаимного угла между векторами с использованием выражения для определения скалярного произведения векторов:


В результате угол между векторами определяется через арккосинус отношения скалярного произведения к произведению модулей векторов.
Однако следует отметить, что функция арккосинус имеет область значений, которая ограничивается интервалом 
Если 



Если 



В результате мы получим, что область значений будет ограничиваться интервалом 
Рассмотрим реализацию рассмотренного выше алгоритма определения взаимного угла между векторами в программном обеспечении Matlab/Simulink.
Рис.3. Реализация в программном обеспечении Matlab/Simulink
Для преобразования аналогового сигнала в вектор используется блок «Fourier», который из периодического сигнала определяет амплитуду и фазу. Также имеется возможность преобразовать вектор через вещественные и мнимые составляющие с помощью использования блока «Magnitude-Angle to Complex» и блока «Complex to Real-Imag».
Рис.4. А лгоритм определения вещественной и мнимой составляющей комплексного числа из аналогового сигнала
Взаимный угол между двумя рассматриваемыми векторами определяется с помощью использования математических блок-элементов в программном обеспечении Matlab/Simulink.
В качестве блока, который позволяет выбрать значение между положительным и отрицательным числом, используется ключ «Switch» на вход которого поступает логический сигнал «0» или «1». В зависимости от поступающего логического сигнала выбирается одно из двух значений взаимного угла.
В результате получена вторая модель определения взаимного угла между аналоговыми сигналами в Matlab/Simulink область значений которой определена на интервале 
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
Видео:Угол между векторами. 9 класс.Скачать

Угол между двумя векторами matlab
Видео:Как находить угол между векторамиСкачать

Художественные модели для рисования — эталонные изображения для рисования фигур (NON-NUDE SERIES DLDS # 6) в Ultra HD 4K
Я хочу рассчитать угол между двумя векторами V = [Vx Vy Vz] а также B = [Bx By Bz] . эта формула верна?
и есть ли другой способ его вычислить?
Мой вопрос не в том, чтобы нормализовать векторы или сделать это проще. Я спрашиваю, как получить угол между этими двумя векторами
- 1 Кажется, это скорее вопрос математики, чем вопрос программирования.
- 1 В зависимости от вашего языка вы должны добавить круглые скобки, чтобы убедиться, что продукт оценивается до разделения. Если оценивать слева направо, это было бы неправильно.
Судя по этой ссылке, это кажется наиболее стабильным решением:
- 1 Вот почему я запутался и не знаю, какой из них правильный и почему
- 2 Просто прочитайте больше по предоставленной мной ссылке. Оба они верны в теории, но на практике этот вариант упоминается для обеспечения более стабильных результатов (в то время как альтернатива с acos вычисляет немного быстрее).
Вариантов очень много:
Все формулы из этой ветки mathworks. Говорят, что а3 самая стабильная, но я не знаю почему.
За несколько векторов хранящиеся в столбцах матрицы, можно вычислить углы с помощью этого кода:
Вы можете вычислить VdotB намного быстрее и для векторов произвольной длины с помощью оператора точки, а именно:
Кроме того, как упоминалось в комментариях, в Matlab есть функция точки для прямого вычисления внутренних продуктов.
Кроме того, формула такова, что вы делаете правильно.
- 4 Если вы хотите быть лаконичным, по крайней мере рекомендую V*B’
- 1 Есть ли причина, по которой вы избегаете внутреннего dot функция?
- @HighPerformanceMark Не говоря уже о том, чтобы забыть о его существовании.
- нет, нет причин, и функция точки работает очень хорошо, но я просто написал такой вопрос.
Эта функция должна возвращать угол в радианах.
Решение Денниса Джахеруддина отлично подходит для трехмерных векторов, для векторов более высокой размерности я бы предложил использовать:
Это исправляет числовые проблемы, из-за которых аргумент acos может быть чуть выше 1 или ниже -1. Однако все еще проблематично, когда один из векторов является нулевым вектором. Этот метод также требует всего 3 * N + 1 умножения и 1 sqrt. Однако для этого также требуются 2 сравнения, в которых метод atan не требуется.
Видео:Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Smnggeophysics
Видео:Нахождение угла между векторами через координаты. 9 класс.Скачать

Угол между двумя векторами matlab
- Главная
-
- Угол между двумя векторами matlab
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Определение угла между двумя векторами
Я хочу рассчитать угол между двумя векторами V = [Vx Vy Vz] а также B = [Bx By Bz] . эта формула верна?
и есть ли другой способ его вычислить?
Мой вопрос не в том, чтобы нормализовать векторы или сделать это проще. Я спрашиваю, как получить угол между этими двумя векторами
- 1 Кажется, это скорее вопрос математики, чем вопрос программирования.
- 1 В зависимости от вашего языка вы должны добавить круглые скобки, чтобы убедиться, что продукт оценивается до разделения. Если оценивать слева направо, это было бы неправильно.
Судя по этой ссылке, это кажется наиболее стабильным решением:
- 1 Вот почему я запутался и не знаю, какой из них правильный и почему
- 2 Прочтите больше по предоставленной мной ссылке. Оба они верны в теории, но на практике этот вариант упоминается для обеспечения более стабильных результатов (в то время как альтернатива с acos вычисляет немного быстрее).
Вариантов очень много:
Все формулы из этой ветки mathworks. Говорят, что а3 самая стабильная, но я не знаю почему.
За несколько векторов хранящиеся в столбцах матрицы, можно вычислить углы с помощью этого кода:
Вы можете вычислить VdotB намного быстрее и для векторов произвольной длины с помощью оператора точки, а именно:
Кроме того, как упоминалось в комментариях, в Matlab есть функция точки для прямого вычисления внутренних продуктов.
Кроме того, формула такова, что вы делаете правильно.
- 4 Если вы хотите быть лаконичным, по крайней мере рекомендую V*B’
- 1 Есть ли причина, по которой вы избегаете внутреннего dot функция?
- @HighPerformanceMark Не говоря уже о том, чтобы забыть о его существовании.
- нет, нет причин, и функция точки работает очень хорошо, но я просто написал такой вопрос.
Эта функция должна возвращать угол в радианах.
Решение Денниса Джахеруддина отлично подходит для трехмерных векторов, для векторов более высокой размерности я бы предложил использовать:
Это исправляет числовые проблемы, из-за которых аргумент acos может быть чуть выше 1 или ниже -1. Однако все еще проблематично, когда один из векторов является нулевым вектором. Этот метод также требует всего 3 * N + 1 умножения и 1 sqrt. Однако для этого также требуются 2 сравнения, в которых метод atan не требуется.
🔍 Видео
11 класс, 5 урок, Угол между векторамиСкачать

Скалярное произведение векторов. 9 класс.Скачать

Математика это не ИсламСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

9 класс, 17 урок, Угол между векторамиСкачать

100 тренировочных задач #135 Угол между векторамиСкачать

Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать

Угол между прямыми в пространстве. 10 класс.Скачать

Все типы 2 задание векторы ЕГЭ по математике профиль 2024Скачать

Косинус угла между векторами. Коллинеарность векторовСкачать

Задание 3 ЕГЭ профиль #121Скачать
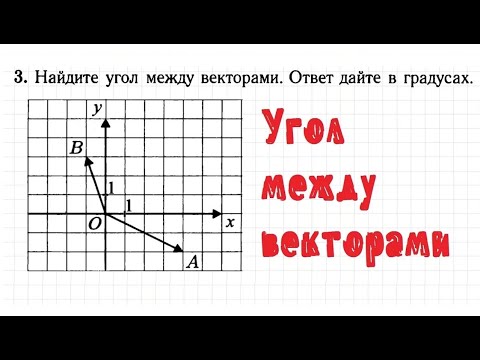
105. Угол между векторамиСкачать










