Пожалуй сложно назвать геодезические купола чем-то необычным или новым. В этой заметке я расскажу немного об этих конструкциях в общем, об их устройстве, а также покажу на примере как я кое что на эту тему считал. Код тоже будет.
Википедию цитировать не буду. Почему я выбрал купол в качестве дома?
- При равном объеме площадь поверхности сферы будет меньше, чем у любой другой формы. Это положительно влияет как на материалоемкость, так и на энергозатраты при эксплуатации.
- Мне нравится как выглядит сфера.
- Это интересный инженерный проект, в каком-то смысле даже вызов. Это сложно, трудно и потому весело!
Как это геодезические сферы устроены вообще? С первого взгляда кажется, что это какое-то переплетение рёбер и уловить систему сложно. В этой заметке попробуем разобраться.
В основе таких конструкций лежит икосаэдр или октаэдр. В общем правильный многогранник.
В моем случае это был именно икосаэдр и чаще используют его. Далее берем одну грань и заменяем ее на несколько треугольников, вершины которых лежат на сфере, центр которой совпадает с центром икосаэдра. Звучит не слишком складно. Отвлечемся.
Есть замечательный калькулятор www.acidome.ru который позволяет в реальном времени покрутить геодезик. Берем в качестве основы icosahedron, ставим частоту 1, часть сферы 1/1.
Это и есть наш основной икосаэдр. Частота это на сколько частей мы разобьем каждое ребро икосаэдра. Ставим 3,4, 5 и ничего становится непонятно. Переключаем в режим кровли и ищем пятиугольники. В тех местах, где у нас вершина икосаэдра — будет пятиугольник. Между тремя пятиугольниками грань икосаэдра.
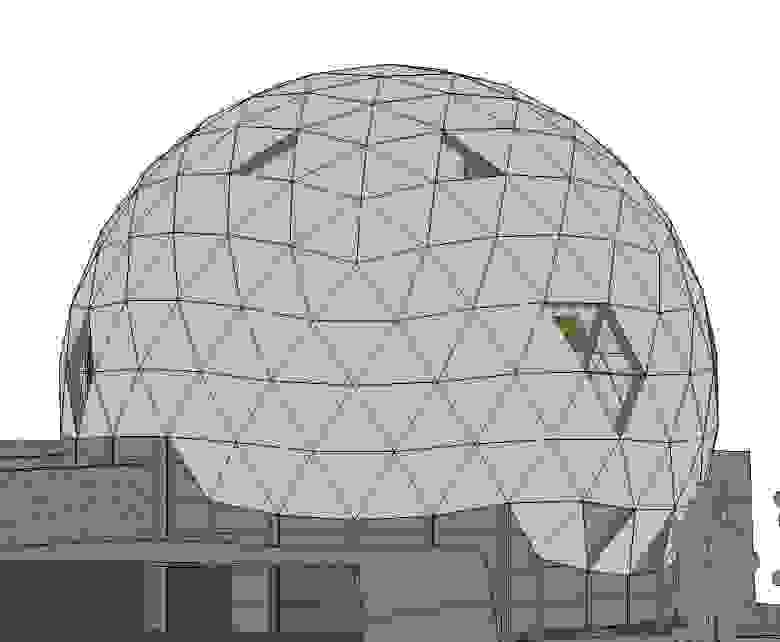
Если внимательно смотреть на геодезик и знать, что искать (обычно пятиугольник), то становится видна регулярность структуры. На Биосфере в Монреале при должном усердии можно найти пятиугольники и посчитать частоту. Частота у нас равна количеству ребер между двумя пятиугольниками.
Сами “большие” треугольники, с вершинами на вершинах икосаэдра также имеют структуру. На acidome в режиме кровли это видно по цвету. Треугольники расположены симметрично относительно центра “большого” треугольника. Количество их типов меньше общего числа треугольников. В случае с частотой 5 уникальных треугольников 9.
В процессе проектирования дома я столкнулся с задачей постройки сферы в Dynamo. Это такой инструмент, который позволяет научить Autodesk Revit работать со сложными формами. Такая среда визуального программирования.
Погуглив я даже нашел скетч, который в Dynamo строил геодезическую сферу. Сферу то он строил, да не ту.
Дело вот в чем. Когда мы берем одно ребро икосаэдра и делим его на мелкие треугольники — сделать это можно несколькими способами. В acidome за это отвечает переключатель “метод разбиения”.
Найденный скетч строил сферу методом равных хорд. Что это значит? Мы берем большой треугольник икосаэдра, каждое его ребро делим на нужное нам количество частей, соединяем точки на ребрах между собой и получаем плоскую сетку из треугольников. Затем эту сетку мы проецируем на сферу. Все бы хорошо, но сами эти треугольники достаточно сильно отличаются по размеру. Центральный больше всех. Оно и понятно, центр “большого” треугольника у нас на максимальном расстоянии от сферы. Это плохо, так как в этом случае сложнее оптимизировать расход материалов. Будет больше отходов.
Другой метод разбиения (равными дугами) предполагает, что мы строим поверх “большого” треугольника дуги и уже их делим на равные части. Подход отличается, простой проекцией не обойтись.
Скетч не подходил. Я попытался его исправить и в итоге мне пришлось нырнуть в это дело с головой.
Как оказалось помимо визуальной среды Dynamo имеет встроенный Python. С этим языком я ранее не сталкивался, но где наша не пропадала? В конце концов это просто инструмент.
Дальше будут кусочки кода, прошу обратить внимание, что это мой hello world в python, а целью было не построить максимально эффективное и производительное решение, а построить нужную сферу.
- Метод равных дуг.
- Строительство и обустройство теплицы в виде геодезического купола на дачном участке
- Чем привлекательны конструкции в форме купола
- Как самостоятельно построить купольную теплицу
- Принципы конструирования купольного каркаса
- Формула расчета длины элементов купола
- Подготовка к монтажу каркаса
- Полевые работы и монтаж основания
- Сборка и обшивка каркаса
- Внутреннее обустройство геотеплицы
- Геодезический купол. Об устройстве и моем опыте расчетов
- Немного истории
- Как правильно производить расчет длин стропильных частей?
- Рейтинг блогов и записей Живого Журнала
- Купольные дома: примеры и обзор технологий строительства
- Дом сфера – прихоть архитектора или подсказка природы?
- Примеры и разновидности купольных конструкций
- Особенности строительства
- Достоинства и интерьер купольных домов
- 📽️ Видео
Метод равных дуг.
Берем одну из граней икосаэдра и из углов этого треугольника строим дуги.
Затем дуги делим на равные части и соединяем точки на дугах новыми дугами. У всех дуг один центр — центр сферы. Точки соединяем не все со всеми, а одноименные. На картинке оно выглядит попроще, чем в коде.
Опа, а дуги то не пересекаются! Не слишком беглое гугление вывело меня на книгу, которая подтвердила мои предположения о том, что нужно в качестве вершины ребра геодезика использовать центр треугольника, образованного пересечением дуг. Также курил исходники acidome, но не помню нашел ли там этому подтверждение. Помню, что было интересно.
Центры надо как-то найти. Это центр треугольника и это не сложно, но нужно было понять где же у нас в ворохе точек эти треугольники. Мне показалось самым простым вариантом соединять ближайшие друг к другу точки.
Теперь нам нужно соединить между собой собранные на разных этапах точки, которые и являются вершинами ребер геодезической сферы. На картинке эти точки видно хорошо, но вот когда они в массиве — все сложнее. Было несколько вариантов, но так как задача была с наименьшими трудозатратами получить рабочий скрипт, вышло вот это:
Сегмент готов. Наверное существует какой-то правильный путь для решения этой задачи, но я проложил свой.
Дальше сегмент разворачивается, несколько раз копируется копируется и получается полная сфера. Вот один из поворотов:
Скриптик вышел страшненький, я его пару раз переписывал, так как были проблемы с экспортом в Revit. Думал, что проблемы с построением. В итоге на форуме Dynamo индус подсказал украинцу и все удалось!
Теперь можно строить сферу любой частоты и любого диаметра. Сравнение размеров с результатами acidome показало, что все сходится с высокой точностью. Повторяемость это хорошо.
Также я занялся оптимизацией размеров с целью минимизации обрезков. Так как все размеры были у меня на руках это было не так трудно. В итоге радиус сферы получился 5,65 метров при частоте 5. Такие размеры позволяют мне достаточно эффективно использовать материалы шириной 125 см. Такую ширину имеют листы OSB, листового металла, утеплителя, гипсокартона. При хорошей оптимизации количество обрезков минимально. Наилучших результатов можно добиться путем расчета раскладок треугольников на материале, но этим я не занимался.
Дальше было проще, так как Revit съел сложную форму и позволил с ней работать примерно с тем же успехом, что и с квадратно-параллельной.
Конечно, трудности на этом не закончились, но это уже совсем другая история.
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Строительство и обустройство теплицы в виде геодезического купола на дачном участке
Теплица на даче давно стала не только подспорьем в выращивании овощей, но еще и возможностью реализовать свои творческие амбиции. Среди всех новаторских решений особого внимания заслуживает геодезический купол – детище современной архитектуры. Интерес к оригинальной конструкции объясняется просто – установить такую теплицу на своем участке под силу даже неопытному мастеру – полусфера легко собирается из простых деталей, а производительность ее грядок не уступает урожаям из стандартных сооружений.
Видео:#2 Расчет купольных домов сферические теплицы Geodesic dome calculatorСкачать

Чем привлекательны конструкции в форме купола
Рост популярности купольных теплиц объясняется несколькими факторами:
- Для установки не нужен прочный фундамент, так как ее конструкция значительно легче, чем аналогичные по площади привычные укрытия.
- Сооружение легко монтируется и разбирается, при необходимости его несложно перенести на новое место.
- Полусферическая форма отличается высокой прочностью и стабильностью. Ячеистый каркас лучше противостоит сильным ветрам, легко выдерживает снегопады и обладает хорошей сейсмоустойчивостью.
- По сравнению с традиционными формами укрытий, строительство теплицы-купола обходится дешевле, так как для монтажа не требуется сложное оборудование. В строительстве используются простые доступные материалы – деревянные бруски или пластиковые трубки для каркаса, шурупы, поликарбонат, агроволокно или парниковую пленка для обшивки.
- За счет уникальной секционной структуры отпадает необходимость в установке внутренних опор, а это существенно экономит стройматериалы.
- В отличие от прямоугольных теплиц в полусфере, не нужно ориентировать грядки относительно сторон света – растения всегда хорошо освещены.
В геокуполе легко обеспечить необходимый микроклимат для выращивания нескольких урожаев огородных культур за год. Грунт всегда хорошо прогревается, а для поддержания стабильности температуры используются экологичные тепловые аккумуляторы – резервуары с водой.
Видео:Сравнение прочности купола из треугольников и из трапеций!Скачать

Как самостоятельно построить купольную теплицу
Построить такое сооружение на своем участке несложно. Для этого потребуется рассчитать размеры секций, распечатать схему сборки, подготовить детали каркаса, расчистить место для установки теплицы и можно приступать к монтажу.
Принципы конструирования купольного каркаса
По своей сути все геодезические купола – это многогранники, грани которых образовывают поверхность, максимально приближенную по форме к сфере. Форма граней может быть разной, но треугольник считается самым стабильным и устойчивым. Поэтому в большинстве случаев основным структурным элементом для создания полусферического каркаса является треугольник.
Для строительства каркаса малых купольных строений на дачных участках – теплиц, беседок, гостевых домиков – чаще всего применяют каркасно-щитовую технологию на основе равнобедренных треугольников разного размера. Чем меньше размер секций, тем больше их потребуется для создания сферического парника. Принцип их соединения между собой похож на пошив футбольного мяча – треугольники соединяются в выпуклые шести- и пятиугольники, которые объединены в устойчивую полусферу.
Совет! Если при расчете геокупола не учитывались углы соединения фрагментов, то монтаж лучше проводить при помощи коннекторов с 4, 5 и 6 лопастями.
Формула расчета длины элементов купола
Чтобы не ошибиться в процессе сборки, нужно заранее все высчитать длину всех ребер, правильную последовательность их чередования, углы соединения элементов. Для составления оптимальной схемы необходимо пользоваться специальными формулами. В основу расчета геодезического купола ложатся конкретные размеры:
- радиус основы сооружения;
- высота теплицы (выраженная в дробном отношении к диаметру сферы, H);
- частота разбивки на секции (V).
Чем выше числовой индекс V (1, 2, 3…), тем больше типов ребер потребуется подготовить. Купол 1V – это усеченный икосаэдр, все ребра одной длины. Такое сооружение больше похоже на пирамиду с пятью гранями. Для строительства домашней теплицы лучше всего подходят купола 2V (два вида ребер, H= радиусу) и 3V (ребра А, В, С, высота сооружения Н= 5/8, 7/12, 5/12 диаметра).
Длина каждого вида ребер (La, Lв, Lс…) рассчитывается по формуле L=R*K, где R – это радиус основания каркаса, а K – коэффициент по частоте разбивки.
Для вычисления необходимого количества материала для обшивки используют формулу расчета площади сферы: S=2π *R*H, где R – радиус основания, а H – вычисленная высота теплицы. Например, при радиусе основания 3V теплицы 4 м и высоте 3/8d, расчет площади будет таким:
S=2*3,14*4*(3/8*8) = 75,36 м2
Подготовка к монтажу каркаса
При строительстве геодезического купола своими руками для каркаса нужно выбирать легкий и прочный материал – деревянные бруски, нетяжелые металлические пруты или пластиковые трубы. Деревянные бруски перед покраской лучше пропитать противогрибковым составом. При подготовке фрагментов крайне важно соблюдать точность разметки – все детали одного типа должны быть взаимозаменяемы.
Совет! Окрашивайте ребра одинаковой длины одним цветом. Например: ребра А – красные, В – синие, С – желтые. Для облегчения работы с цветной схемой сборки маркировка готовых ребер должна совпадать с маркировкой на чертеже.
Количество ребер по типам и коннекторов для монтажа каждого вида купола высчитывается по схемам.
Полевые работы и монтаж основания
Для установки геодезического купола на даче необходимо выбрать открытый незатененный участок. Плодородную почву с площадки можно временно удалить, а саму поверхность засыпать глиной и тщательно выровнять и утрамбовать. Если почва неустойчивая, то под основание придется залить небольшой фундамент или вбить опорные сваи под каждый угол основы (форма фигуры повторяет очертания нижнего ряда схемы – десяти-, восьми- или двенадцатиугольник).
Высота основания зависит от того, как предполагается использовать постройку – для легкого летнего парника хватит 15-20 см, а для зимней теплицы с теплыми грядками лучше поднять стенки на 50-70 см. Основу обычно изготавливают из толстого бруса или деревянных щитов. Невысокое временное сооружение можно установить прямо на кирпичи или камни, уложенные под углы нижнего ряда каркаса.
Сборка и обшивка каркаса
Конструкцию собирать лучше снизу-вверх, соединяя ребра коннекторами или шурупами в соответствии со схемой. Вершину купола удобнее собрать на земле, и только потом прикрепить к каркасу. Заниматься монтажом такого «конструктора для взрослых» лучше с помощником – так удобнее фиксировать детали. Для входа во время сборки вместо нескольких элементов купола вставляется дверная коробка.
Совет! Для вентиляции установите в верхней части купола 2 рамки-форточки, изготовленные по внутренним размерам треугольного элемента.
Следующий этап – обшивка каркаса. Для этих работ выбирается плотный прозрачный материал – парниковая пленка, поликарбонат или стекло. Существует несколько способов укрыть купольную теплицу:
- готовый каркас обтягивают пленкой поверху;
- вырезают треугольники из поликарбоната (по размеру каждой ячейки каркаса) и крепятся, как мозаика;
- в ячейки каркаса вставляют стекло.
После того как купол полностью обшит, нужно проверить его герметичность. При необходимости места соединения реек и обшивки дополнительно герметизируют.
Видео:Последний треугольник в каркас купола ГудКармаСкачать

Внутреннее обустройство геотеплицы
Сборка геокупола своими руками завершена, самое время обустроить его внутри. До закладывания грядок необходимо подготовить системы обогрева, полива и вентиляции. Внутри купола по северной стороне необходимо закрепить блестящий материал (фольгу, металлизированную пленку) – так растения и резервуары с водой получат больше света и тепла.
Температура в теплице поддерживается с помощью самодельных аккумуляторов тепла – под светоотражающим щитом устанавливают несколько бочек с водой. Вода за день нагреется, благодаря чему ночью внутри будет поддерживаться необходимая температура. Эту же воду можно использовать для капельного полива.
Для обогрева грядок под слоем почвы можно уложить гофрированные трубы, в которые будет подаваться теплый воздух.
Трубы засыпают слоем навоза или компоста. Теплый воздух циркулирует по системе под грядками благодаря вентилятору, подключенному к солнечной батарее. Дополнительно для аккумуляции тепла в центре теплицы можно установить несколько пятилитровых фляг, также заполненных водой. Кроме встроенных форточек, можно установить автоматическую систему вентиляции для проветривания по расписанию.
Грядки в купольной теплице располагают по периметру.
Ширину грядки лучше делать не больше, чем 1,5 м, иначе тяжело ухаживать за растениями. Какую именно грядку обустроить – дело вкуса. Можно построить стандартные – до 40 см в высоту, высокие или теплые, вертикальные или двухъярусные. При большом радиусе основания в центре обычно обустраивают грядку-клумбу, на которой высаживают высокорослые или вьющиеся культуры.
Геодезические теплицы на природном обогреве подходят для выращивания любых культур в период с ранней весны и до ноября. При достаточно большом объеме купола и наличии дополнительного отопления и подсветки такие теплицы пригодны для круглогодичного использования даже в районах с умеренным климатом.
Как видите, самостоятельно построить на участке оригинальную теплицу-купол несложно. И если учесть, что затраты на ее создание и содержание несколько меньше, чем для других укрытий, то можно смело сказать, что популярность таких сооружений будет расти с каждым годом.
Видео:Простой расчёт развёртки конусаСкачать

Геодезический купол. Об устройстве и моем опыте расчетов
Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

Немного истории
Геодезические купола — архитектурные сооружения с несущей сетчатой оболочкой впервые появились в конце 40-х годов прошлого века. Патент на это изобретение получил американец Ричард Фуллер. Необычные строения должны были решить проблему быстрого возведения недорогого комфортабельного жилья. Для массовой застройки идея не прижилась, но активно используется для строительства футуристических кафе, бассейнов, стадионов.
Не менее популярны сферы и среди ландшафтных дизайнеров. Такие строения достаточно просторны и могут быть использованы для самых разных целей. Их необычный вид сразу притягивает внимание, они становятся центром пейзажной композиции.
Геодезический купол обладает большой несущей способностью, к тому же его можно построить из простых материалов в самые короткие сроки без привлечения бригад специалистов и техники. Так, купол высотой в 50 метров можно построить силами трех человек без привлечения строительного крана.
Видео:SketchUp: Как создать геодезический купол?Скачать

Как правильно производить расчет длин стропильных частей?
Обязательно обратите внимание, при пользовании калькулятором, на то, что использование коннектора другого вида, который отличается от представленного в видеоролике, может повлечь за собой необходимость в изготовлении стропильных частей других длин.
Всё будет зависеть от того, какое расстояние между болтовыми соединениями стропильных частей, исходя из этого, уже и следует производить правильный расчет длины.
Также обратите внимание и на то, что коннекторы могут быть пятилучевыми или шестилучевыми, все зависит от места их размещения в конструкции самого каркаса купольного дома и от того, сколько стропил, они будут соединять.
На въезде вашей территории загородного дома мы рекомендуем установить ворота с автоматикой и аксессуарами безопасности. Такими автоматическими воротами будет не только комфортно управлять, но и совершенно безопасно.
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Рейтинг блогов и записей Живого Журнала
Расчет геодезического купола производится по заданному радиусу (площади поверхности основания), с целью получить:
- Расчетные размеры ребер и их количество
- Количество и тип требуемых коннекторов
- Значения углов между ребрами
- Требуемые высоту, общую площадь постройки
- Площадь поверхности купола
Площадь основания купола ассчитывается по заданному радиусу S=π *R2. При этом надо учитывать, что реальная площадь получится несколько меньше, вследствие того, что радиус купола считается, обычно, по внешней поверхности полусферы (по «вершинам»), и стенки купола имеют также определенную толщину.
| Геодезический купол — не чистая сфера, апроксимация приводит к тому, что в основании лежит не круг, а многоугольник, вписанный в заданную окружность. Площадь такого многоугольника заведомо меньше площади круга. |
Высота геодезического купола пределяется по заданному диаметру, и может быть для четной частоты разбиения 1/2, 1/4 диаметра (при большой частоте может быть и 1/6, 1/8). Для нечетной — 3/8, 5/8 диаметра (и т.д.).
| 4V, 1/4 сферы | 4V, 1/2 сферы |
Площадь поверхности геодезического купола ассчитывается по известной формуле расчета площади сферы S=4π *R2. Для купола, равного 1/2 сферы, формула будет иметь вид S=2π *R2. В более сложному случае, когда речь идет о площади сегмента, сферы, формула расчета S=2π *RH, где H — высота сегмента.
Расчет конструктивных элементов геодезического купола ожно производить с использованием готовых таблиц, в которых заданы:
- Количество ребер купола одинаковой длины — ребра A, B, C, D, E, F, G, H, I. У купола с частотой 1V одно ребро — A. У купола с частотой 2V два ребра — A, B. У купола с частотой 3V три ребра — A, B, C. И т.д.
- Количство и тип используемых коннекторов — 4-х конечные, 5-ти конечные, 6-ти конечные.
- Коэффициенты пересчета длин ребер купола на радиус купола. К примеру, если вы хотите построить купол с частотой 2V высотой 1/2 и радиусом 3,5 метра, вам надо величину радиуса (3,5) умножить на коэффициент 0,61803 для определения длины ребра А, и умножить на коэффициент 0,54653 для определения длины ребра B. Получим: А=2,163м, В=1,912м.
1V купол
| Ребра | Коэффициенты | Количество |
| A | 1.05146 | 25 |
| 5-ти конечный коннектор | 6 | |
| 4-х конечный коннектор | 5 | |
2V купол
| Ребра | Коэффициенты | Количество для 1/2 |
| A | 0,61803 | 35 |
| B | 0,54653 | 30 |
| 4-х конечный коннектор | 10 | |
| 5-ти конечный коннектор | 6 | |
| 6-ти конечный коннектор | 10 | |
3V купол
| Ребра | Коэффициенты | Количество для 3/8 | Количество для 5/8 |
| A | 0,34862 | 30 | 30 |
| B | 0,40355 | 40 | 55 |
| C | 0,41241 | 50 | 80 |
| 4-х конечный коннектор | 15 | 15 | |
| 5-ти конечный коннектор | 6 | 6 | |
| 6-ти конечный коннектор | 25 | 40 | |
4V купол
| Ребра | Коэффициенты | Количество для 1/2 |
| A | 0,25318 | 30 |
| B | 0,29524 | 30 |
| C | 0,29453 | 60 |
| D | 0,31287 | 70 |
| E | 0,32492 | 30 |
| F | 0,29859 | 30 |
| 4-х конечный коннектор | 20 | |
| 5-ти конечный коннектор | 6 | |
| 6-ти конечный коннектор | 65 | |
5V купол
| Ребра | Коэффициенты | Количество для 5/8 |
| A | 0,19814743 | 30 |
| B | 0,23179025 | 30 |
| C | 0,22568578 | 60 |
| D | 0,24724291 | 60 |
| E | 0,25516701 | 70 |
| F | 0,24508578 | 90 |
| G | 0,26159810 | 40 |
| H | 0,23159760 | 30 |
| I | 0,24534642 | 20 |
| 4-х конечный коннектор | 25 | |
| 5-ти конечный коннектор | 6 | |
| 6-ти конечный коннектор | 120 | |
6V купол
| Ребра | Коэффициенты | Количество для 1/2 |
| A | 0,1625672 | 30 |
| B | 0,1904769 | 30 |
| C | 0,1819083 | 60 |
| D | 0,2028197 | 90 |
| E | 0,1873834 | 30 |
| F | 0,1980126 | 60 |
| G | 0,2059077 | 130 |
| H | 0,2153537 | 65 |
| I | 0,2166282 | 60 |
| 4-х конечный коннектор | 30 | |
| 5-ти конечный коннектор | 6 | |
| 6-ти конечный коннектор | 160 | |
Углы между ребрами между «лепестками» коннекторов) легко вычисляются по заданным сторонам треугольников.
Приблизительные значения углов апроксимации, в которых сходятся ребра геодезического купола на его вершинах:
- 1V купол — А=32º
- 2V купол — A=18º, B=16º
- 3V купол — A=10º, B=12º, С=12º
- 4V купол — A, B, С, D, E, F — 7-9º
- 5V купол — A, B, С, D, E, F, G, H, I — 6-7º
- 6V купол — A, B, С, D, E, F, G, H, I — 5-6º
Калькуляторы on-line:
Acidome calculator толковый российский on-line калькулятор
Geo-Dome
Tags: купол




Видео:ГудКарма - принцип сборки купольного каркаса, особенности монтажа | Айсдом.рфСкачать

Купольные дома: примеры и обзор технологий строительства
В представлении большинства людей жилой дом – прямоугольная коробка под скатной крышей.
К конструкциям сферического и купольного очертания отношение двоякое. Привлекая внимание необычным «космическим» видом у многих они вызывают сомнения в надежности и удобстве проживания.
Преодолеть сложившийся «кубический» стереотип, объективно изучить достоинства и недостатки купольных домов, оценить возможность их самостоятельного строительства вам поможет эта статья.
Дом сфера – прихоть архитектора или подсказка природы?
Начнем с того, что многие выдающиеся изобретения человек позаимствовал у природы, наблюдая за жизнью животных. Давайте обратим внимание на «технологии», используемые птицами при строительстве своих жилищ. Нетрудно заметить, что здесь нигде нет прямых углов. Полусферы, шары, окружности – только такие формы признает природа. Получается, что столь любимая нами жилая «коробка» вовсе не является венцом творения.
Обратив внимание на этот природный феномен, инженеры исследовали механические свойства сферических и купольных конструкций. Оказалось, что они не только обладают отличной аэродинамикой, но и намного прочнее прямоугольных.
Энергетически сферическая поверхность безупречна. При максимальном внутреннем объеме она имеет минимальную площадь. Поэтому в купольном строении потери тепла во внешнюю среду в несколько раз меньше, чем в обычном доме. Не зря обитатели арктики эскимосы веками строили сферические домики «иглу» из снега. Практический опыт подсказал им, какой должна быть ветростойкая и энергоэффективная конструкция.
В наши дни сферические дома из области теоретики перешли в разряд практических технологий экологического строительства. Тысячи людей во всем мире успели оценить их преимущества и не жалеют о своем выборе.
Примеры и разновидности купольных конструкций
Сферическую конструкцию можно построить двумя способами:
- В виде геодезического купола (собирается из треугольных каркасных ячеек, стыкуемых с помощью узловых элементов — коннекторов).
- Из гнутых стоек или сегментов арочной формы, соединяемых вершинами (стратодезический купол).
Гнутоклееные деревянные стойки для сборки стратодезического купола
По технологии стратодезического купола собирают «маковки» православных храмов. Геодезический купол пришел к нам из Америки. Его изобретателем считают инженера Фуллера.
Несмотря на различия во внешнем виде, эти конструкции отличаются минимальным весом, высокой жесткостью и устойчивостью.
Дома в форме сферы можно строить из любого материала, начиная от пенопласта и заканчивая бетоном. Выбор конкретного варианта зависит от технической оснащенности исполнителя. Для возведения жилых зданий чаще всего используют конструкции с деревянным каркасом.
Причин для этого несколько. Древесина – экологичный и прочный материал, обладающий высокой упругостью. Геодезические купола собирают из деревянных балок, соединяя их стальными коннекторами.
Каркас дома на основе геодезического купола
Стратодезические жилые конструкции строят из гнутоклееных балок.
Каркас здания на основе стратодезического купола
Японская технология сферических зданий основана на использовании гнутых пенопластовых блоков с замками. Из них собирают небольшие одноэтажные постройки. Пенопласт в таком доме выполняет сразу две функции: конструкционного материала и утеплителя.
Современный домик-«иглу» строится не из снега, а из пенопластовой «скорлупы»
Минимальный вес дома-сферы позволяет возводить его на мелкозаглубленном ленточном или свайном фундаменте. Для утепления секций используют минвату, солому, эковату или пенопласт.
Наиболее распространенный вид кровельного покрытия – мягкая битумная черепица. Этот материал идеально ложится на криволинейные поверхности.
Дом-сфера, покрытый битумной черепицей
Сторонники экостроительства делают выбор в пользу деревянного гонта – тонких дощечек, образующих оригинальное чешуйчатое покрытие.
Деревянный гонт естественно смотрится на сферическом здании Двухуровневый дом на основе стратодезического купола с гонтовой облицовкой
Недавно на рынке появились новые материалы, идеально адаптированные для создания бесшовного кровельного ковра. Это «жидкая пробка» (частицы пробкового дерева в акриловом полимере) и жидкая резина.
Как мы уже говорили, материал для строительства сферического дома может быть разнообразным. Если вам больше нравится бетон, нет проблем.
Используя технологию набрызга, можно возводить купольные постройки из легкого бетона
Современные технологии позволяют строить такие дома с помощью пневмоопалубки из ПВХ, на которую наносится вспененный утеплитель. Затем по утеплителю ставят арматурный каркас и наносят на него бетонную смесь методом торкретирования.
Из одних соломенных блоков дом-сферу не построишь. Этот материал используют как утеплитель. Солому плотно набивают в ячейки из досок и собирают из них купол.
Пространственный каркас выполнен из деревянных ячеек, наполненных соломой
Особенности строительства
Еще совсем недавно дом-купол был строительной экзотикой. За его возведение брались энтузиасты экологического движения и любители оригинальных конструкций. Сегодня интернет наполнен заводскими комплектами сферических домов. Необычное жилище на основе геодезического купола и стратодезическую конструкцию можно купить, не выходя из городской квартиры.
Тем же, кто предпочитает все делать собственными руками, мы рекомендуем остановиться на геодезическом куполе. В сборке он немного сложнее дома-сферы из полуарок, но зато не требует сложного оборудования для гнутья и склеивания древесины.
Самый ответственный узел конструкции – коннектор. От точности его изготовления зависит пространственная стыковка всех элементов. Поэтому для работы лучше купить готовый заводской комплект.
Следующий шаг – подготовка ребер каркаса из деревянных брусков толщиной 50 мм. Их ширина должна быть равной толщине утеплителя (минимум 10 см). Длину ребер выбирают, ориентируясь на сборочную схему геокупола.
Необходимое пояснение: в расчетах купольных каркасов используется термин «частота» или «сечение», обозначаемые символом V. Им определяется плотность разбивки поверхности купола на треугольники. Чем больше частота, тем менее «угловатой» и более шарообразной получается купольная конструкция.
Однако, увеличение частоты вызывает рост количества ребер и коннекторов, существенно усложняя конструкцию. Поэтому на практике чаще всего строят купольные дома с частотой 2V.
Частота разбивки (V) поверхности купола – базовый элемент расчетов
Кроме частоты нужно определиться с диаметром купола и его высотой. Если вы купите готовый комплект коннекторов, то пользоваться онлайн калькулятором для расчета длин ребер вам не придется. Изготовитель делает коннекторы для сборки каркаса заданной высоты и диаметра.
Как показывает практика, купол диаметром 8 метров и высотой 4 метра оптимален для сооружения двухуровневого дачного дома общей площадью 64 м2, зимнего сада или сауны.
Для того, чтобы построить купольный дом своими руками нужно выполнить несколько операций:
- Разметить на участке фундамент под каркас (ленточный, столбчатый, «шведская плита» или свайный).
- На стадии бетонирования заложить в фундамент анкера. Они нужны для крепления подкладочного бруса, к которому фиксируют первый ряд «треугольников» каркаса.
- Сборку ведут параллельными рядами, связывая ребра каркаса в пространственную конструкцию с помощью коннекторов.
- Завершив монтаж, купол изнутри обшивают деревянной вагонкой или гипсокартонном.
- В ячейки каркаса закладывают утеплитель, накрывают его ветрозащитной мембраной и обшивают снаружи плитой Изоплат или OSB.
- В местах установки окон обшивку не делают. В зоне установки дверей каркас «разрывают», оставляя в нем нишу нужного размера. Жесткость геодезического купола очень высокая, поэтому дверные проемы не могут ее существенно уменьшить.
Двухуровневый дом-сфера на стадии наружной обшивки плитой OSB
Некоторые застройщики делают первый этаж в виде многогранника, а второй венчают геокуполом.
Дверной проем идеально вписывается в дизайн сферического здания. А вот треугольные окна и доборные элементы дверной коробки обходятся дороже обычных. Их приходится заказывать как нестандартные изделия.
Достоинства и интерьер купольных домов
Кроме упомянутых преимуществ – уникальной прочности и ветростойкости, сферические строения обладают и другими достоинствами:
- экономичностью (за счет легкого фундамента, сборки без привлечения кранов, использования эффективного утеплителя);
- возможностью свободной планировки жилого пространства благодаря отсутствию внутренних стен;
- отличными звукоизоляционными качествами;
- привлекательным внешним видом и уникальным интерьером.
Внутри круглые здания на удивление вместительны и красивы. Большая высота позволяет без проблем размещать в них второй этаж.
Даже под небольшим 4-х метровым куполом можно разместить комфортную баню. Сферическая форма и центральное расположение печи обеспечивают экономию тепла и равномерный прогрев помещений.
Сауна под куполом – компактно и удобно
Характер отзывов о купольных домах в большинстве своем положителен. Владельцам нравится оригинальная форма, комфорт и вместительность этих построек.
Экономия энергоносителей, низкие затраты на строительство сферических зданий также часто упоминаются в комментариях их хозяев.
Из субъективных положительных эмоций следует отметить покой и умиротворенность, ощущаемые человеком в таком доме.
📽️ Видео
Как высчитать квадратуру из треугольника,трапеции и т. д.Скачать

купольная теплица своими руками (диаметр 6 метров)Скачать

ОГЭ. ПРО ЗОНТИКСкачать

Как сделать геокупол? | Геодезический купол своими рукамиСкачать

Расчет купольной теплицы диметром 6 метров, радиус 3 метра, стоимость теплицы. Все по уму.Скачать

Огэ.9кл.Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найтиСкачать

Расчет купольной конструкцииСкачать

Запомни: все формулы для площади треугольникаСкачать

Задания 1-5 Задача про зонтСкачать

Каркас геокуполов для глэмпинга и мероприятий. Основа конструктива сферы. Распаковка купола ЗСКСкачать

Купол из композитной арматуры - 1.Скачать