Золотые треугольники мона лиза

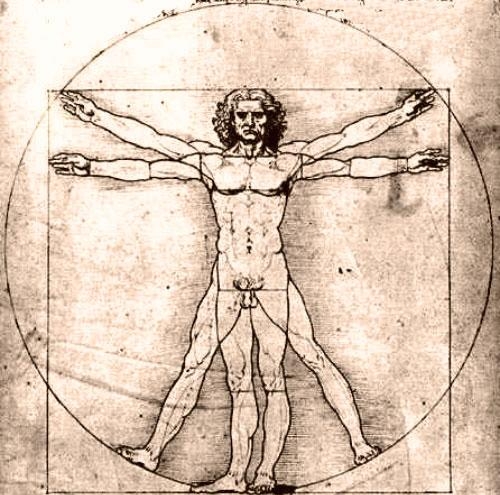
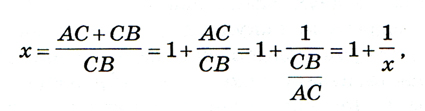Главная → Статьи → Золотое сечение

Весь наш мир можно описать числами. Многие числа играют настолько значительную роль в этом описании, что имеют собственные имена: Пи, экспанента (е) и т.д. Среди этих «именных» чисел есть весьма замечательное. Математики, художники, архитекторы в разные времена называли его «золотое число», «божественное число», «божественное сечение». Термин «золотое сечение» придумал Клавдий Птолемей, а популярным он стал благодаря Леонардо Да Винчи, который широко использовал его в своих работах. Люди искусства заметили, что пропорции форм, которые особенно приятны глазу для восприятия, в основе своей имеют «золотое сечение».

***
Известнейшим математическим сочинением античной науки являются «Начала» Евклида. Именно из «Начал» к нам пришла геометрическая задача «о делении отрезка в крайнем и среднем отношении». Что и является самим «Золотым сечением».
Суть задачи такова:
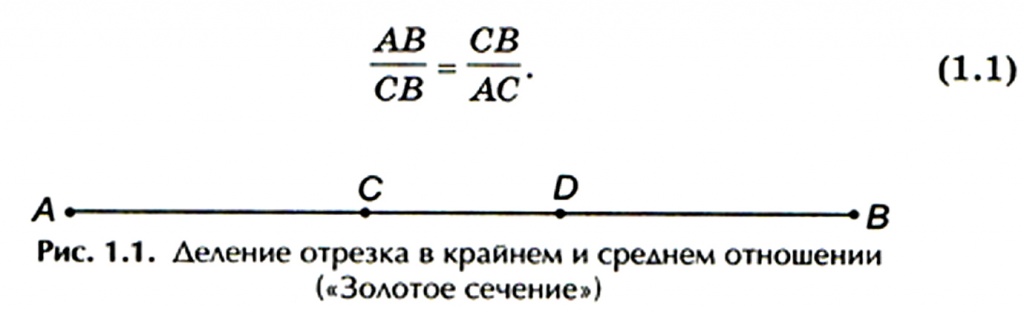
Разделим отрезок АВ точкой С в таком отношении, чтобы большая часть отрезка СВ так относилась к меньшей части отрезка АС, как отрезок АВ к своей большей части СВ, т. е.

Обозначим пропорцию (1.1) через х. Тогда, учитывая, что АВ = АС + СВ, пропорцию (1.1) можно записать в следующем виде:

откуда вытекает следующее алгебраическое уравнение для вычисления искомой пропорции х:

х* = х + 1. (1.2)
x* — в квадрате

Из «физического смысла» пропорции (1.1) вытекает, что искомое решение уравнения (1.2) должно быть положительным числом, откуда вытекает, что решением задачи о делении отрезка в крайнем и среднем отношении является положительный корень уравнения (1.2), который мы обозначим через , то есть

Приближенное значение золотой пропорции равно:
= 1,61803 39887 49894 84820 45868 34365 63811 77203…

ЗОЛОТЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ

На основе вышеизложенных пропорций в геометрии определены такие понятия золотых геометрических фигур:
— золотой прямоугольник (в котором отношение большей стороны к меньшей равно золотой пропорции);
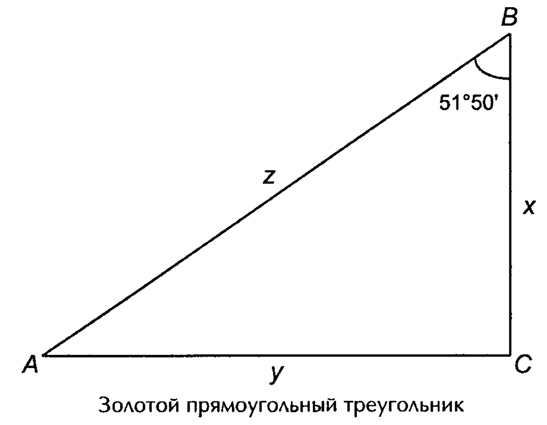
— золотой прямоугольный треугольник;
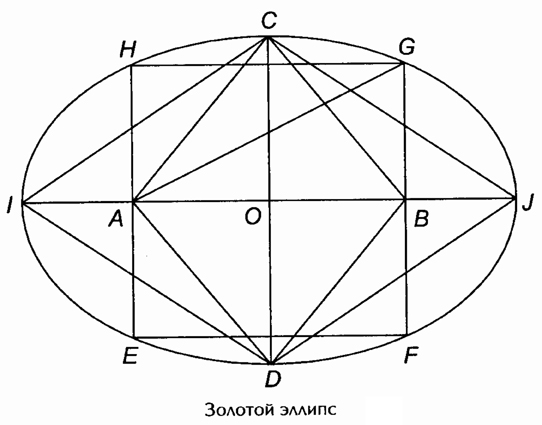
— золотой эллипс;
— золотой равнобедренный треугольник.

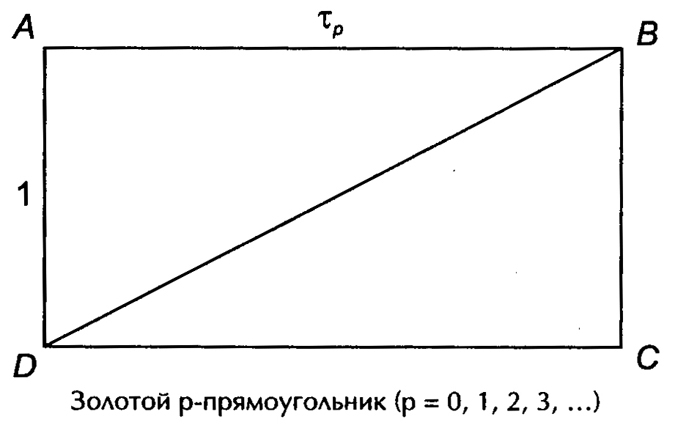
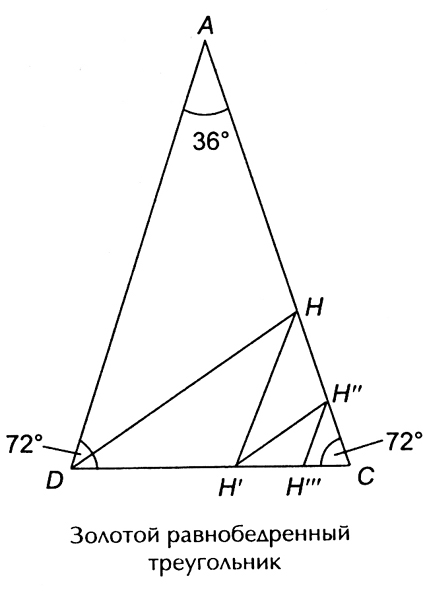
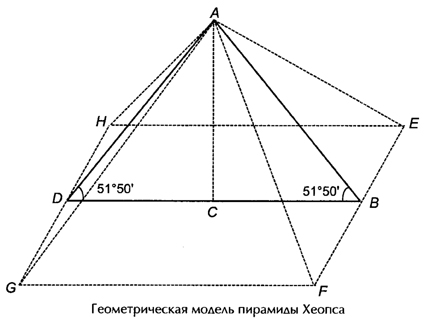
Прямоугольный треугольник со сторонами 3:4:5 называется «совершенным», «священным» или «египетским».
Создатели египетских пирамид выбрали в качестве «главной геометрической идеи» для пирамиды Хеопса – золотой прямоугольный треугольник, а для пирамиды Хефрена – «священный» треугольник.

Пентагон («pentagonon» — греч.), правильный пятиугольник. Если в пентагоне провести все диагонали, то в результате мы получим пятиугольную звезду, называемую пентаграммой («pentagrammon» — греч.: «pente» — пять и «grammon» — линия) или пентаклом.

Пентаграмма, называемая в народных поверьях «ведьминой стопой», играла большую роль во всех магических науках и рассматривалась как средство защиты от злых духов.
Каждые восемь лет планета Венера описывает абсолютно правильный пентакл по большому кругу небесной сферы.
Здание «Пентагона», военного ведомства США имеет форму пентагона.

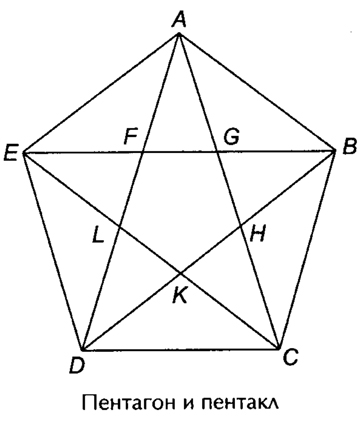
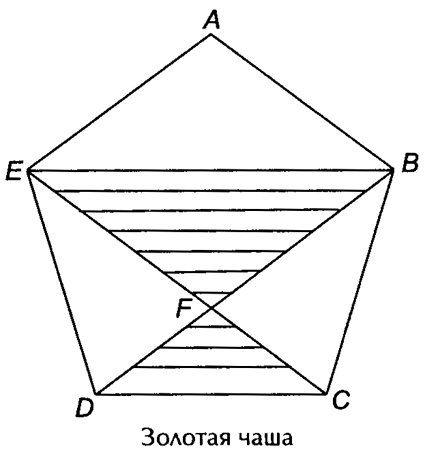
Пентагон и пентакл включают в себя ряд замечательных фигур, которые широко использовались в произведениях искусства. В античном искусстве широко известен так называемый закон золотой чаши, которые использовали античные скульпторы и золотых дел мастера. Заштрихованная часть пентагона дает схематическое представление золотой чаши.

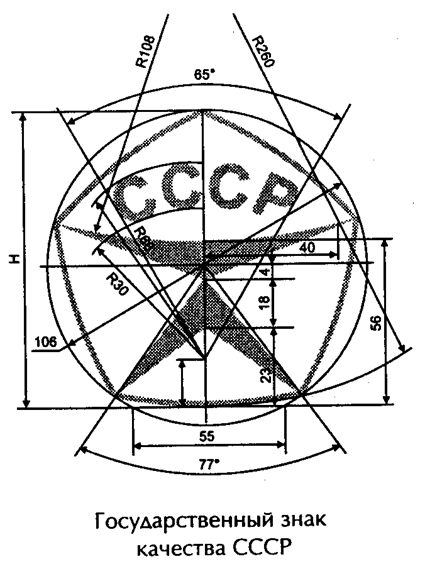
Когда-то в Советском Союзе существовал Государственный знак качества, в котором явно просматриваются мотивы золотой чаши.

В живой природе широко распространены формы, основанные на пентагональной симметрии – морские звезды, морские ежи, цветы..

ГАРМОНИЯ ЗОЛОТОГО СЕЧЕНИЯ
(краткий обзор истории искусства)

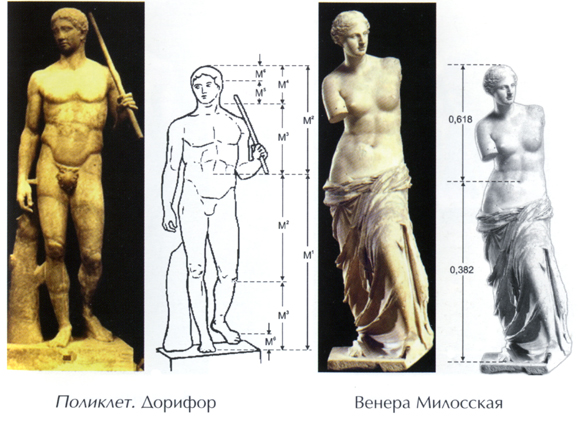
Эталоном красоты человеческого тела, образцом гармонического телосложения издав-на и по праву считаются великие творения греческих скульпторов: Фидия, Поликтета, Мирона, Праксителя. В своих творениях греческие мастера использовали принцип золотой пропорции. Одним из высших достижений классического греческого искусства может служить статуя Дорифора, изваянная Поликтетом в V веке до н. э. Эта статуя считается наилучшим примером для анализа пропорций идеального человеческого тела, установленных античными греческими скульпторами, и напрямую связана с Золотым сечение. М=0,618…
Венера Милосская, статуя богини Афродиты и эталон женской красоты, является од-ним из лучших памятников греческого скульптурного искусства.

Леонардо Да Винчи использовал пропорции Золотого сечения во многих своих самых знаменитых произведениях, и в частности, в «Тайной вечере» и знаменитой «Джоконде».
Исследователи картины «Джоконда» обнаружили, что композиционное построение кар-тины основано на двух золотых треугольниках, повернутых друг к другу своими основаниями. Гармонический анализ картины показывает, что зрачок левого глаза, через который проходит вертикальная ось полотна, находится на пересечении двух биссектрис верхнего золотого треугольника, которые с одной стороны, делят пополам углы при основании золотого треугольника, а с другой стороны, в точках пересечения с бедрами золотого треугольника делят их в пропорции Золотого сечения. Таким образом, Леонардо Да Винчи использовал в своей картине не только принцип симметрии, но и Золотое сечение.

Картина «Святое семейство» Микеланджело признана одним из шедевров западноевропейского искусства эпохи Возрождения. Гармонический анализ показал, что композиция картины основана на пентакле.

Пропорции статуи Давида (работы Микеланджело) основаны на Золотом сечении.

Яркий пример архитектуры барокко, Смольный собор в Санкт-Петербурге, производит неизгладимое впечатление. В его основных пропорциях так же усматривается Золотое сечение.

На знаменитой картине Ивана Шишкина «Корабельная роща» просматриваются мотивы Золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит картину Золотым сечением по горизонтали. Справа от сосны – освещенный солнцем при-горок. Он делит картину Золотым сечением по вертикали. Слева от главной сосны находится много сосен – можно продолжить деление Золотым сечением по горизонтали левой части картины. Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении Золотого сечения, придает ей характер уравновешенности и спокойствия.

Строительство штаб-квартиры ООН в Нью-Йорке было завершено в 1943 году. Здание привлекло тогда всеобщее внимание не только как общественное сооружение, созданное с применением новейших архитектурных средств, но и как первый пример использования сплошного солнцемодулирущего экрана на одном из фасадов. В этом здании также просматриваются мотивы Золотого сечения. В композиции здания четко выделяются три поставленных друг на друга золотых прямоугольника, которые и являются его главной архитектурной идеей.

Любое музыкальное произведение имеет временное протяжение и делится некоторыми «эстетическими вехами» на отдельные части, которые обращают на себя внимание и облегчают восприятие в целом. Этими вехами могут быть динамические и интонационные кульминационные пункты музыкального произведения. Отдельные временные интервалы музыкального произведения, соединяемые «кульминационным событием», как правило, находятся в соотношении Золотого сечения. В музыкальных произведениях различных композиторов обычно констатируется не одно Золотое сечение, а целая серия подобных сечений. Наибольшее количество произведений, в которых имеется Золоте сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).

Если музыка – гармоническое упорядочение звуков, то поэзия – гармоническое упорядочение речи. Четкий ритм, закономерное чередование ударных и безударных слогов, упорядоченная размерность стихотворений, их эмоциональная насыщенность делают поэзию родной сестрой музыкальных произведений. Золотое сечение в поэзии в первую очередь проявляется как наличие определенного момента стихотворения (кульминации, смыслового перелома, главной мысли произведения) в строке, приходящейся на точку деления общего числа строк стихотворения в золотой пропорции. Так, если стихотворение содержит 100 строк, то первая точка Золотого сечения приходится на 62-ю строку (62%), вторая – на 38-ю (38%) и т. д. Произведения Александра Сергеевича Пушкина, и в том числе «Евгений Онегин» — тончайшее соответствие золотой пропорции! Произведения Шота Руставели и М.Ю. Лермонтова также построены по принципу Золотого сечения.

Один из современных видов искусства – кинематограф, — вобравший в себя драматургию действия, живопись, музыку. В выдающихся произведениях киноискусства право-мерно искать проявления Золотого сечения. Первым это сделал создатель шедевра мирового кино «Броненосец «Потемкин» кинорежиссер Сергей Эйзенштейн. В построении этой картины он сумел воплотить основной принцип гармонии – Золотое сечение. Как отмечает сам Эйзенштейн, красный флаг на мачте восставшего броненосца (точка апогея фильма) взвивается в точке золотой пропорции, отсчитываемой от конца фильма.

В течение многих тысячелетий Золотое сечение было объектом восхищения и поклонения выдающихся ученых и мыслителей: Пифагора, Платона, Евклида, Луки Пачоли, Иоганна Кеплера, Павла Флоренского…
В настоящее время Золотое сечение оказывается источником новых плодотворных идей в математике и теоретической физике, биологии и ботанике, экономике и компьютерной науке…

Материал сформирован по книге «Код да Винчи и ряды Фибоначчи» А. Стахова, А. Слученковой, И. Щербакова, 2007 года выпуска, издательства «Питер».

Видео:Загадка Моны ЛизыСкачать

The Jizn

Видео:Секреты Моны ЛизыСкачать

Золотое сечение Фибоначчи. Божественная мера красоты

Давайте выясним, что общего между древнеегипетскими пирамидами, картиной Леонардо да Винчи «Мона Лиза», подсолнухом, улиткой, сосновой шишкой и пальцами человека? Ответ на этот вопрос сокрыт в удивительных числах, которые были открыты итальянским математиком средневековья Леонардо Пизанским, более известным по именем Фибоначчи (род. ок. 1170 — умер после 1228), итальянский математик. Путешествуя по Востоку, познакомился с […]

Давайте выясним, что общего между древнеегипетскими пирамидами, картиной Леонардо да Винчи «Мона Лиза», подсолнухом, улиткой, сосновой шишкой и пальцами человека?

Ответ на этот вопрос сокрыт в удивительных числах, которые были открыты итальянским математиком средневековья Леонардо Пизанским, более известным по именем Фибоначчи (род. ок. 1170 — умер после 1228), итальянский математик. Путешествуя по Востоку, познакомился с достижениями арабской математики; способствовал передаче их на Запад.

После его открытия числа эти так и стали называться именем известного математика. Удивительная суть последовательности чисел Фибоначчи состоит в том, что каждое число в этой последовательности получается из суммы двух предыдущих чисел.

Итак, числа, образующие последовательность:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …

называются «числами Фибоначчи», а сама последовательность — последовательностью Фибоначчи.

В числах Фибоначчи существует одна очень интересная особенность. При делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом всегда будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то пpевосходящая, то не достигающая его. (Прим. иррациональное число, т.е. число, десятичное представление которого бесконечно и не периодично)

Более того, после 13-ого числа в последовательности этот результат деления становится постоянным до бесконечности ряда… Именно это постоянное число деления в средние века было названо Божественной пропорцией, а ныне в наши дни именуется как золотое сечение, золотое сpеднее или золотая пропорция. В алгебpе это число обозначается гpеческой буквой фи (Ф)

Итак, Золотая пропорция = 1 : 1,618

233 / 144 = 1,618

377 / 233 = 1,618

610 / 377 = 1,618

987 / 610 = 1,618

1597 / 987 = 1,618

2584 / 1597 = 1,618

Видео:Похищение Моны Лизы | Как картина Леонардо да Винчи стала легендойСкачать

Тело человека и золотое сечение

Художники, ученые, модельеры, дизайнеры делают свои расчеты, чертежи или наброски, исходя из соотношения золотого сечения. Они используют мерки с тела человека, сотворенного также по принципу золотой сечения. Леонардо Да Винчи и Ле Корбюзье перед тем как создавать свои шедевры брали параметры человеческого тела, созданного по закону Золотой пропорции.

Самая главная книга всех современных архитекторов справочник Э.Нойферта «Строительное проектирование» содержит основные расчеты параметров туловища человека, заключающие в себе золотую пропорцию.

Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными. Принцип расчета золотой меры на теле человека можно изобразить в виде схемы:

Первый пример золотого сечения в строении тела человека:
Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618.

Кроме этого есть и еще несколько основных золотых пропорции нашего тела:

* расстояние от кончиков пальцев до запястья до локтя равно 1:1.618;

* расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618;

* расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1.618;

* расстояние точки пупа до коленей и от коленей до ступней равно 1:1.618;

* расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1.618;

* расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618;

* расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618:

Золотое сечение в чертах лица человека как критерий совершенной красоты.

В строении черт лица человека также есть множество примеров, приближающихся по значению к формуле золотого сечения. Однако не бросайтесь тотчас же за линейкой, чтобы обмерять лица всех людей. Потому что точные соответствия золотому сечению, по мнению ученых и людей искусства, художников и скульпторов, существуют только у людей с совершенной красотой. Собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора.

К примеру, если мы суммируем ширину двух передних верхних зубов и разделим эту сумму на высоту зубов, то, получив при этом число золотого сечения, можно утверждать, что строение этих зубов идеально.

На человеческом лице существуют и иные воплощения правила золотого сечения. Приведем несколько таких соотношений:

* Высота лица / ширина лица;

* Центральная точка соединения губ до основания носа / длина носа;

* Высота лица / расстояние от кончика подбородка до центральной точки соединения губ;

* Ширина рта / ширина носа;

* Ширина носа / расстояние между ноздрями;

* Расстояние между зрачками / расстояние между бровями.

Видео:ФАКТЫ О МОНА ЛИЗЕ КОТОРЫЕ ВЫ НЕ ЗНАЛИСкачать

Рука человека

Достаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг.

* Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца);

* Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения;

* У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи:

Видео:САМЫЕ ИНТЕРЕСНЫЕ ФАКТЫ О МОНА ЛИЗЕСкачать

Золотая пропорция в строении легких человека

Американский физик Б.Д.Уэст и доктор А.Л. Гольдбергер во время физико-анатомических исследований установили, что в строении легких человека также существует золотое сечение.

Особенность бронхов, составляющих легкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче.

* Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.

Видео:Почему Мона Лиза так знаменита 😮Скачать

Строение золотого ортогонального четырехугольника и спирали

Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

В геометрии прямоугольник с таким отношением сторон стали называть золотым прямоугольником. Его длинные стороны соотносятся с короткими сторонами в соотношении 1,168 : 1.

Золотой прямоугольник также обладает многими удивительными свойствами. Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов (например, раковинах улиток).

Полюс спирали лежит на пересечении диагоналей начального прямоугольника и первого отрезаемого вертикального. Причем, диагонали всех последующих уменьшающихся золотых прямоугольников лежат на этих диагоналях. Разумеется, есть и золотой треугольник.

Английский дизайнер и эстетик Уильям Чарлтон констатировал, что люди считают спиралевидные формы приятными на вид и используют их вот уже тысячелетия, объяснив это так:

«Нам приятен вид спирали, потому что визуально мы с легкостью можем рассматривать ее.»

Видео:4 лица Моны ЛизыСкачать

В природе

* Лежащее в основе строения спирали правило золотого сечения встречается в природе очень часто в бесподобных по красоте творениях. Самые наглядные примеры — спиралевидную форму можно увидеть и в расположении семян подсолнечника, и в шишках сосны, в ананасах, кактусах, строении лепестков роз и т.д.;

* Ботаники установили, что в расположении листьев на ветке, семян подсолнечника или шишек сосны со всей очевидность проявляется ряд Фибоначчи, а стало быть, проявляется закон золотого сечения;

Всевышний Господь каждому Своему творению установил особую меру и придал соразмерность, что подтверждается на примерах, встречающихся в природе. Можно привести великое множество примеров, когда процесс роста живых организмов происходит в строгом соответствии с формой логарифмической спирали.

Все пружинки в спирали имеют одинаковую форму. Математики установили, что даже при увеличении размеров пружинок форма спирали остается неизменной. В математике нет более иной формы, которая обладала бы такими же уникальными свойствами как спираль.

Видео:МОНА ЛИЗА: история кражи века или почему Джоконда - самая дорогая картина в мире? Леонардо Да ВинчиСкачать

Строение морских раковин

Ученые, изучавшие внутреннее и внешнее строение раковин мягкотелых моллюсков, обитающих на дне морей, констатировали:

«Внутренняя поверхность раковин безупречно гладкая, а внешняя вся покрыта шероховатостями, неровностями. Моллюск был в раковине и для этого внутренняя поверхность раковины должна была быть безупречно гладкой. Внешние углы-изгибы раковины увеличивают ее крепость, твердость и таким образом повышают ее прочность. Совершенство и поразительная разумность строения ракушки (улитки) восхищает. Спиральная идея раковин является совершенной геометрической формой и удивительна по своей отточенной красоте.»

У большинства улиток, которые обладают раковинами, раковина растет в форме логарифмической спирали. Однако нет сомнения, что эти неразумные существа не имеют представления не только о логарифмической спирали, но не обладают даже простейшими математическими знаниями, чтобы самим создать себе спиралевидную раковину.

Но тогда как же эти неразумные существа смогли определить и избрать для себя идеальную форму роста и существования в виде спиральной раковины? Могли ли эти живые существа, которых ученых мир называет примитивными формами жизни, рассчитать, что идеальной для их существования будет логарифмическая форму ракушки?

Конечно же нет, потому что такой замысел невозможно осуществить без наличия разума и знаний. Но таковым разумом не обладают ни примитивные моллюски, ни бессознательная природа, которую, правда, некоторые ученые называют создательницей жизни на земле(?!)

Пытаться объяснить происхождение подобной даже самой примитивной формы жизни случайным стечением неких природных обстоятельств по меньшей мере абсурдно. Совершенно ясно, что этот проект является осознанным творением.

Биолог Сэр Д`арки Томпсон этот вид роста морских раковин называет «форма роста гномов».

Сэр Томпсон делает такой комментарий:

«Нет более простой системы, чем рост морских ракушек, которые растут и расширяются соразмерно, сохраняя ту же форму. Раковина, что самое удивительное, растет, но никогда не меняет формы.»

Наутилус, размером в несколько сантиметров в диаметре, представляет собой самый выразительный пример гномового вида роста. С.Моррисон так описывает этот процесс роста наутилуса, спланировать который даже человеческим разумом представляется довольно сложным:

«Внутри раковины наутилуса есть множество отделов-комнат с перегородками из перламутра, причем сама раковина внутри представляет собой спираль, расширяющуюся от центра. По мере роста наутилуса в передней части ракушки нарастает еще одна комнатка, но уже больших размеров, чем предыдущая, а перегородки оставшейся позади комнатки покрываются слоем перламутра. Таким образом, спираль все время пропорционально расширяется.»

Приведем лишь некоторые типы спиралевидных раковин имеющих логарифмическую форму роста в соответствии с их научными названиями:
Haliotis Parvus, Dolium Perdix, Murex, Fusus Antiquus, Scalari Pretiosa, Solarium Trochleare.

Все обнаруженные ископаемые останки раковин также имели развитую спиральную форму.

Однако логарифмическая форма роста встречается в животном мире не только у моллюсков. Рога антилоп, диких козлов, баранов и прочих подобных животных также развиваются в виде спирали по законам золотой пропорции.

Видео:Мона Лизу испачкали тортом в Лувре | Вандал пытался разбить защитное стекло «Джоконды» ЛеонардоСкачать

Золотое сечение в ухе человека

Во внутреннем ухе человека имеется орган Cochlea («Улитка»), который исполняет функцию передачи звуковой вибрации. Эта костевидная структура наполнена жидкостью и также сотворена в форме улитки, содержащую в себе стабильную логарифмическую форму спирали = 73º 43’.

Видео:Edu: Почему Мона Лиза так знаменита?Скачать

Рога и бивни животных, развивающиеся в форме спирали

Бивни слонов и вымерших мамонтов, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль. Пауки всегда плетут свои паутины в виде логарифмической спирали. Строение таких микроорганизмов, как планктоны ( виды globigerinae, planorbis, vortex, terebra, turitellae и trochida) также имеют форму спирали.

Видео:Числа Фибоначчи и тайна Золотого сеченияСкачать

Золотое сечение в строении микромиров

Геометрические фигуры не ограничиваются только лишь треугольником, квадратом, пяти- или шестиугольником. Если соединить эти фигуры различным образом между собой, то мы получим новые трехмерные геометрические фигуры. Примерами этому служат такие фигуры как куб или пирамида. Однако кроме них существуют также другие трехмерные фигуры, с которыми нам не приходилось встречаться в повседневной жизни, и названия которых мы слышим, возможно, впервые. Среди таких трехмерных фигур можно назвать тетраэдр (правильная четырехсторонняя фигура), октаэдр, додекаэдр, икосаэдр и т.п. Додекаэдр состоит из 13-ти пятиугольников, икосаэдр из 20-и треугольников. Математики отмечают, что эти фигуры математически очень легко трансформируются, и трансформация их происходит в соответствии с формулой логарифмической спирали золотого сечения.

В микромире трехмерные логарифмические формы, построенные по золотым пропорциям, распространены повсеместно. К примеру, многие вирусы имеют трехмерную геометрическую форму икосаэдра. Пожалуй, самый известный из таких вирусов — вирус Adeno. Белковая оболочка вируса Адено формируется из 252 единиц белковых клеток, расположенных в определенной последовательности. В каждом углу икосаэдра расположены по 12 единиц белковых клеток в форме пятиугольной призмы и из этих углов простираются шипообразные структуры.

Впервые золотое сечение в строении вирусов обнаружили в 1950-хх гг. ученые из Лондонского Биркбекского Колледжа А.Клуг и Д.Каспар. 13 Первым логарифмическую форму явил в себе вирус Polyo. Форма этого вируса оказалась аналогичной с формой вируса Rhino 14.

Возникает вопрос, каким образом вирусы образуют столь сложные трехмерные формы, устройство которых содержит в себе золотое сечение, которые даже нашим человеческим умом сконструировать довольно сложно? Первооткрыватель этих форм вирусов, вирусолог А.Клуг дает такой комментарий:

«Доктор Каспар и я показали, что для сферической оболочки вируса самой оптимальной формой является симметрия типа формы икосаэдра. Такой порядок сводит к минимуму число связующих элементов… Большая часть геодезических полусферических кубов Букминстера Фуллера построены по аналогичному геометрическому принципу. 14 Монтаж таких кубов требует чрезвычайно точной и подробной схемы-разъяснения. Тогда как бессознательные вирусы сами сооружают себе столь сложную оболочку из эластичных, гибких белковых клеточных единиц.»

Комментарий Клюга еще раз напоминает о предельно очевидной истине: в строении даже микроскопического организма, который ученые классифицируют как «самую примитивную форму жизни», в данном случае в вирусе, присутствует четкий замысел и осуществлен разумный проект 16. Этот проект несопоставим по своему совершенству и точности исполнения с самыми передовыми архитектурными проектами, созданными людьми. К примеру проектами, созданными гениальным архитектором Букминстером Фуллером.

Трехмерные модели додекаэдра и икосаэдра присутствуют также и в строении скелетов одноклеточных морских микроорганизмов радиолярий (лучевиков), скелет которых создан из кремнезёма.

Радиолярии формируют свое тело весьма изысканной, необычной красоты. Форма их составляет правильный додекаэдр. Причем из каждого его угла прорастает псевдоудлиннение-конечность и иные необычные формы-наросты.

В качестве примеров микроорганизмов, воплощающих в своем строении эти трехмерные геометрические фигуры, приведем Circigonia Icosahedra с икасаэдральным строением скелета и Circorhegma Dodecahedra с додекаэдральным строением скелета, причем размеры этих микроорганизмов не достигают и одного миллиметра.

Видео:ДА ВИНЧИ И ЕГО ГЛАВНАЯ ТАЙНА | ЧТО СКРЫВАЕТ МОНА ЛИЗА | ЗАПРЕТНЫЕ ИЗОБРЕТЕНИЯСкачать

Золотые пропорции в строении молекулы ДНК

Все сведения о физиологических особенностях живых существ хранятся в микроскопической молекуле ДНК, строение которой также содержит в себе закон золотой пропорции. Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем — одна стомиллионная доля сантиметра).

21 и 34 — это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618

Видео:Мона Лиза (Джоконда), Леонардо да Винчи - анализ картиныСкачать

Золотое сечение в строении снежинок

Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом. Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору.

Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотого сечения.

Видео:Вандал с тортом и розами напал на Джоконду в ЛувреСкачать

Золотые пропорции в космическом пространстве

Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения.

Видео:Мона Лиза масломСкачать

Золотое сечение в физике

Последовательность чисел Фибоначчи и формула золотого сечения непосредственным образом затрагивает и сферу физики и физических законов:

«Представим две соприкоснувшиеся между собой стеклянные пластины. Теперь направим на них луч света. Часть луча пройдет сквозь стекло, другая часть поглотиться, оставшаяся же часть отразится от стекла. Произойдет явление «множественного отражения». Количество путей, которые проходит луч внутри стекла, прежде чем пройти и выйди сквозь стекло, зависит от количества лучей, который не прошли сквозь стекло, а подверглись отражению. Если подсчитать количество лучей, отразившихся от стекла и прошедших сквозь него, то опять же мы получим последовательность чисел Фибоначчи в соотношении 1:1.618.»

Строение всех встречающихся в природе живых организмов и неживых объектов, не имеющих никакой связи и подобия между собой, спланировано по определенной математической формуле. Это является самым ярким доказательством их осознанной сотворенности согласно некоему проекту, замыслу. Формула золотого сечения и золотые пропорции очень хорошо известны всем людям искусства, ибо это главные правила эстетики. Любое произведение искусства, спроектированное в точном соответствии с пропорциями золотого сечения, являет собой совершенную эстетическую форму.

Видео:10 загадок Моны Лизы Леонардо да ВинчиСкачать

Золотые треугольники мона лиза

Мона Лиза

Портрет Моны Лизы (Джоконда) Леонардо да Винчи привлекает тем, что композиция рисунка построена на «золотых треугольниках», точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника.

Леонардо да Винчи (Leonardo da Vinci)
(1452-1519)
— великий итальянский художник и скульптор,
исследователь, инженер-изобретатель, архитектор и механик, химик, ботаник и анатом, философ, поэт и музыкант .

Рождение Венеры
1485г, темпера на холсте, 172.5 x 278.5cм,
Галерея Уффици, Флоренция, Италия.

БОТТИЧЕЛЛИ (Botticelli) Сандро (Алессандро ди Мариано Филипепи) (1445 — 1510),
итальянский живописец. Представитель Раннего Возрождения.

Полотно «Рождение Венеры» написано несколькими годами позже» Весны». Неизвестно, кто из семейства Медичи был ее заказчиком. Мы знаем только, что с середины XVI. века она вместе с «Весной» находилась на вилле Кастелло. Литературными источниками для ее написания были произведения Полициано, Вергилия и Гомера.
На картине изображено не само рождение богини, а последовавший за тем момент, когда она, гонимая дыханием гениев воздуха, достигает берега, где ее встречает одна из граций.Согласно древнейшему греческому поэту Гесиоду («Теогония», 188-200), Венера родилась из моря — из пены, которую произвели гениталии оскопленного Урана ( САТУРН), выброшенные в воду Кроном. Она плывет к берегу в раскрытой раковине, подгоняемой мягким дуновением ветра, и наконец причаливает на Пафосе (на Кипре) — одном из главных мест почитания ее, культа в античности. Ее греческое имя Афродита, возможно, происходит от aphros, что значит «пена».
Около острова Киферы родилась Афродита, дочь Урана, из белоснежной пены морских волн. Легкий, ласкающий ветерок принес ее на остров Кипр. Там окружили юные Оры вышедшую из морских волн богиню любви. Они облекли ее в златотканую одежду и увенчали венком из благоухающих цветов. Где только не ступала Афродита, там пышно разрастались цветы. Весь воздух полон был благоуханием. Эрот и Гимерот повели дивную богиню на Олимп. Громко приветствовали ее боги. С тех пор всегда живет среди богов Олимпа златая Афродита, вечно юная, прекраснейшая из богинь. (Н.А.Кун «Легенды и мифы древней Греции»)

Афинская школа
Рафаэль
Рафаэль не был ученым-математиком, но, подобно многим художникам той эпохи, обладал немалыми познаниями в геометрии. В знаменитой фреске “Афинская школа”, где в храме науки предстоит общество великих философов древности, наше внимание привлекает группа Эвклида — крупнейшего древнегреческого математика, разбирающего сложный чертеж.
Хитроумная комбинация двух треугольников также построена в соответствии с пропорцией золотого сечения: она может быть вписана в прямоугольник с соотношением сторон 5/8. Этот чертеж удивительно легко вставляется в верхний участок архитектуры. Верхний угол треугольника упирается в замковый камень арки на ближнем к зрителю участке, нижний — в точку схода перспектив, а боковой участок обозначает пропорции пространственного разрыва между двумя частями арок.

🌟 Видео

О том, как Пабло Пикассо обвинили в краже "Джоконды"Скачать

11 Скрытых Секретов на Известных КартинахСкачать

Сколько стоит Мона Лиза?Скачать

Если бы Мона Лизу нарисовали в 2022! 😳🤯Скачать