Золотой и серебряный треугольник (8 видео)

Золотой и серебряный треугольник

Как и по какому принципу творятся и живут тело вечного Космоса и многообразные части его тела?

«[Тело космоса] было искусно устроено так, чтобы получать пищу от собственного тления, осуществляя все свои действия и состояния в себе самом и само через себя… Ибо такому телу из семи родов движения он уделил соответствующий род, а именно тот, который ближе всего к уму и разумению. Поэтому он заставил его единообразно вращаться в одном и том же месте, в самом себе, совершая круг за кругом, а остальные шесть родов движения были устранены»[1]. (*Остальные шесть родов движений, как объясняется в примечании, – это вперед, назад, направо, налево, вверх и вниз, связанные с развитием деятельности органов живых существ, зависимых от окружающего мира).

АЛЬТЕРНАТИВНОЕ ГЕОМЕТРИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ «ЗОЛОТОЙ» ПРОПОРЦИИ.

Чем принципиально отличается новое геометрическое решение задачи «золотой» пропорции от традиционно существующего решения (Рис. 1)?

Рис. 1. Исполнение «золотого сечения» отрезка АВ в современной геометрии.

В осуществленном мной решении задачи, отрезок прямой не просто делится на гармоничные части, а он рассматривается, как некая изначальная «порождающая модель» (по Платону). Произвольный отрезок прямой посредством круговых движений сам себя делит на гармоничные части и одновременно является всеобщей мерой бесконечного многообразия форм самоорганизующегося космоса, «космических идей» (отношений) и всех реально существующих частей космоса, «в том числе, конечно и человека… его души и тела». Разумеется, выразить данный тезис одним и даже сотней рисунков невозможно. Поскольку, «Триалектика» — это новый метод познания и наука о началах, то моя задача сужается к тому, чтобы показать принципиально новый метод решения задачи «золотых сечений», а не только его результаты.

Понятно, что, воображая непрерывное круговое движение некой реальной пространственной субстанции, мы не в состоянии моделировать реальность ее форм и беспрерывность ее вращения и кручения посредством циркуля. Посредством циркуля и линейки мы моделируем идеальные, а не реальные формы бытия, их относительные масштабы, разные количественные и пространственные отношения, моделируем идеальные отношения, в согласии с которыми, возможно, они и существуют.

Сравним рисунки альтернативных методов решения задачи.

Рис. 2. Альтернативное геометрическое исполнение
«золотого сечения» отрезка АВ.

ЗОЛОТОЕ СЕЧЕНИЕ ОТРЕЗКА «АВ». НОВЫЙ МЕТОД РЕШЕНИЯ (Рис. 2).

Порядок геометрического решения задачи «золотого» сечения отрезка АВ:

1. Раствором циркуля равному АВ = α чертим окружность с центром в точке А. Таким образом, изначально абстрактный отрезок АВ (алгебраическое решение «Беседа 1»), в новом геометрическом решении «золотого сечения» отрезка обретает статус «порождающей модели». Он становится мерой конкретного круга. То есть АВ становится радиусом – r конкретного круга с центром в точке А.

2. Продолжим отрезок АВ до пересечения его с окружностью в точке Р. Таким образом, ВР = 2r – диаметр окружности.

3. Не меняя раствора циркуля, ставим его ножку в точку Р и чертим дугу до пересечения ее с окружностью в точках Н и Т.

4. Соединяем точки В, Н и Т прямыми линиями и, таким образом получаем первую и основную, по мнению многих, сакральную геометрическую фигуру – равносторонний треугольник, сторона НТ которого в точке О делит радиус круга пополам и сама также делится пополам.

5. Раствором циркуля ОВ восстанавливаем перпендикуляр к диаметру круга в точке А до пересечения его с окружностью в точках E и J. АЕ = r.

6. Раствором циркуля ОЕ чертим дугу от точки Е до пересечения ее с отрезком АВ в точке М.

7. Раствором циркуля РМ чертим дугу от точки М до пересечения ее с окружностью в точке С.

8. Раствором циркуля АМ чертим окружность и отмечаем замечательные точки пересечения L и F.

9. Соединяем прямыми линиями, полученные в результате кругового движения, замечательные точки, где ВР ≈ 1,4142135r – сторона вписанного квадрата. Отрезки АО = ОР = 0,5r, ОМ = ОЕ и РС = РМ – по построению.

Прежде чем приступить к вычислению длин интересующих нас отрезков, приведем замечательную подсказку Платона к нашим построениям и вычислениям:

«Итак, нам приходится отдать предпочтение двум треугольникам, как таким, из которых составлено тело огня и (трех) прочих тел: один из них равнобедренный, а другой таков, что в нем квадрат большей стороны в три раза больше квадрата меньшей» [2].

Таким образом, в итоге круговых движений был построен равнобедренный треугольник ЕОМ (ОМ = ОЕ), разделенный на два прямоугольных треугольника: ОАЕ и МАЕ и равнобедренный прямоугольный треугольник ВАЕ. В согласии с теоремой Пифагора, произведем вычисления сторон названных треугольников:

Так как ОМ = ОЕ, то АМ = ОМ – АО; АМ = 1,1180339r – 0,5r ≈ 0,6180339r.

Отрезок РМ = ОМ + ОР = АМ + АВ;

РМ = 1,1180339r + 0,5r ≈ 0,6180339r + r ≈ 1,6180339r.

МВ = АВ – АМ = r – 0,6180339r ≈ 0,3819661r.

Таким образом, была доказана, скажем так, «не четко сформулированная» Платоном теорема. Любой произвольно взятый отрезок прямой, можно разделить на пропорциональные части «золотых» сечений, мерой круговых вращений самого отрезка.

ОНТОЛОГИЧЕСКИЙ СМЫСЛ МЕРЫ ОТРЕЗКА РАВНОГО 1,6180339……α, при исполнении золотого сечения отрезка АВ, как показано на Рис. 1 нам выяснить не удалось, поскольку такой отрезок отсутствует на рисунке. В этом мы полагаем главный недостаток геометрического решения задачи (Рис. 2). Рис.3 устраняет, указанный недостаток. Но не только в этом и, главным образом, не в этом проявляется достоинство геометрического решения данной фундаментальной задачи! Решая ее в русле разгадок сакральных смыслов, имеющихся в сочинениях Платона, мы приоткрываем новый, более богатый мир геометрии «золотых» геометрических фигур и «золотых» отношений между их сторонами, периметрами и площадями. Для этого произведем еще несколько вычислений на базе Рис. 2.

Таким образом, построен по данному отрезку АВ вписанный прямоугольный треугольник. Такая задача на построение ставится и решается в геометрии впервые. Но не в этом – ценность ее постановки и решения. Ценность ее – в параметрах построенного треугольника, у которого одна сторона (гипотенуза) равна 2АВ, один катет является стороной правильного вписанного пятиугольника, а другой катет – мера «золотого сечения» ≈ 1,6180339r. При этом замечательной точкой F катет РС делится в отношениях «золотого сечения»:

FC : FP = r : 0,6180339r ≈ 1,6180339; FP : PC = 0,6180339r : 1,6180339r ≈ 0,381966.

« ЗОЛОТОЙ» И «СЕРЕБРЯННЫЙ» ТРЕУГОЛЬНИКИ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА.

Стороны «золотого» ΔАЕМ соответственно равны:

сторона АЕ = r – сторона правильного, вписанного в данный круг 6-угольника;

сторона – сторона правильного, вписанного в данный круг 5-угольника;

сторона АМ ≈ 0,6180339r – сторона правильного, вписанного в данный круг 10-угольника.

Площади «золотого» и «серебряного» треугольников относятся как их основания: S_АЕМ : S_АЕО = АМ : АО. Подставив их значения, вычислим:

(0,5•0,6180339) : (0,5•0,5) = 0,6180339 : 0,5; 1,2360676 = 1,2360676.

Стороны «серебряного» ΔОАЕ – суть числа: АЕ = r = 1 – число триединой меры; ОЕ = 1,1180339 – число основания «золотого сечения»; АО = 0,5 – «вещественное» число [3].

«ЗОЛОТОЕ СЕЧЕНИЕ» ПЛОЩАДИ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА

Стороны ВМЕ замечательны тем, что сторона ВЕ равна стороне вписанного квадрата, а МЕ равна стороне вписанного пятиугольника в круг с центром А. Сторона ВМ ≈ 0,382r. Площадь ΔВМЕ составляет пятую часть площади РСВ (0,951 : 0,190 ≈ 5).

Произведем вычисление площадей указанных треугольников:

Площадь ΔВАЕ равна 0,5•АВ•АЕ = 0,5r 2 ;

Площадь АЕМ равна 0,5•АМ•АЕ = 0,5•0,6180339r r ≈ 0,309r 2 ;

Площадь ВМЕ равна 0,5r 2 – 0,309r 2 ≈ 0,19098r 2 .

Произведем вычисление отношений между площадями указанных треугольников:

0,309r 2 : 0,5r 2 ≈ 0,618; 0,191r 2 : 0,5r 2 ≈ 0,382; 0,309r 2 : 0,191r 2 ≈ 1,618 и т.д.

ГЕОМЕТРИЧЕСКОЕ ЧИСЛО ФИЗИЧЕСКОЙ КОНСТАНТЫ ТОНКОЙ СТРУКТУРЫ

Размышляя о мудрости некоторых мер теоретической и экспериментальной физики, в 2001 г. я писал: «Постоянная тонкой структуры или постоянная электромагнитной связи α = (137) -1 = 1/137 = 0,007299270072992700729 — число с тайной. Она фигурирует почти во всех уравнениях электродинамики, но никто до сих пор, не знает, почему она равна именно 1/137 Никто не смог предложить теоретическую формулу для α, объясняющую эту величину, и выводящую ее из известных законов физики. Эмпирических формул за истекшие СТО лет от дней открытия этого таинственного числа было предложено немало. Но эмпирические формулы не объясняют физической сути, стоящей за ними. Экспериментальное значение данной постоянной равно 1/137,03604 = 0,007297350390452 и отличается от значения 1/137… Тайна его откроется, когда наступит тому время» [4].

Обращаю внимание читателя на отрезок LO (Рис.3). Его длина равна:

LO = АL – AO ≈ 0,6180339r – 0,5r ≈ 0,1180339r. Если учесть то, что некая изначальная мера Платоновой «порождающей модели» бытия порождает иерархию фрактальной геометрии и фрактальной физики, то геометрически можно с высокой точностью вычислить безразмерную величину постоянной тонкой структуры или постоянной электромагнитной связи.

Если фрактальный отрезок будет равен 10 -1 LO, тогда

1,6180339r : 0,01180339r ≈ 137,08213 – безразмерная физическая константа тонкой структуры или электромагнитной связи α = 1 :137,08213 ≈ 0,0072948…

Построенная геометрическая «порождающая модель» тонкой структуры отличается от экспериментальной физической безразмерной константы на (137,08213 – 137,03604) ≈ 0,04609.

Таким образом, полученные данные, проведенных мной исследований, дают основание предполагать, что реально существуют и более тонкие лучевые (волновые) структуры по сравнению с электромагнитными.

Наступило время и тайна приоткрылась.

ЛИТЕРАТУРА:

Платон. Собр. соч. в 4-х т. «Мысль», М., 1994. Т.3, с. 436-437.
Платон. Собр. соч. в 4-х т. «Мысль», М., 1994. Т.3, с. 457-458.
Сергиенко П.Я. Триалектика: новое понимание мира. Пущино – 1995., с.19-30.
Сергиенко П.Я. Триалектика. О мерах мудрости и мудрости мер. 82 с. Пущино – 2001.с. 75 – 76.
Сергиенко П.Я. Синтетическая геометрия триалектики. 27с. Пущино – 2003
Сергиенко П.Я. Начала. Триалектика сакральной геометрии. 32с. Пущино – 2005

Содержание

Золотое и серебряное сечение: в чем различия?
Серебрянное сечение: что это такое, чем отличается от золотого.
Исследование золотых фигур
История золотого сечения.
ЗОЛОТОЙ ПРЯМОУГОЛЬНИК.
ЗОЛОТОЙ ТРЕУГОЛЬНИК И ЕГО ИССЛЕДОВАНИЕ.
Применение золотого треугольника при решении задач.
ЗОЛОТАЯ ПИРАМИДА И ЕЕ ИССЛЕДОВАНИЕ.
Исследование золотой пирамиды.
Применение золотой пирамиды при решении задач.
Золотое сечение в картине Леонардо да Винчи «Джоконда»
Золотая спираль в картине Рафаэля «Избиение младенцев»
📸 Видео

Видео:Золотой треугольник | Олимпиадная математикаСкачать

Золотое и серебряное сечение: в чем различия?

Видео:Золотой и Серебряный треугольник ( устно считать стороны в треугольнике)Скачать

Серебрянное сечение: что это такое, чем отличается от золотого.

Золотое сечение – это определенная закономерность, соотношение чисел, при котором большее число относится к меньшему так же, как сумма этих чисел к большему из них. Его можно встретить во многих арт-объектах, особенно в работах древних архитекторов, скульпторов и художников. Сегодня в художественных школах и академиях наставники сознательно рекомендуют ученикам и студентам использовать в своих работах «золотую пропорцию».

Золотое сечение применяют не только в искусстве, но и в точных науках, например в биологии, физике и математике. Возможно, вы не знали, но помимо широко известного уже упомянутого соотношения существуют и другие, так называемые «металлические» сечения, которые практически не изучены и редко применяются на практике. Можно сказать, что при повсеместном использовании золотого другие металлические соотношения отходят на задний план.

Благодаря стараниям двух сингапурских студентов-математиков постепенно все внимание мира вновь возвращается к «металлическим» константам, которые включают, кроме золотого сечения, все корни квадратного уравнения x² — nx = 1 для положительных значений n. Постепенно увеличивающиеся значения уравнения называются серебряным, бронзовым и другими «металлическими» сечениями.

Золотое сечение гораздо более известно, и мы ассоциируем его с раковиной наутилуса гораздо чаще, чем с фактическим представлением о том, что оно на самом деле воплощает. Согласно перефразированному студентами утверждению древнегреческого математика Евклида, «прямая линия обрезается в соответствии с золотым сечением, когда отношение всей линии к более длинному сегменту равно отношению более длинного сегмента к более короткому».

Другими словами, схема пропорциональных отрезков образует золотое сечение, причем «золотые» отрезки постепенно уменьшаются. В своей статье студенты предлагают ознакомиться с интерактивным графиком, где вы можно проследить зависимость спирали от изменения значений n в режиме онлайн.

Каждая пара смежных целых чисел имеет свою собственную «металлическую пропорцию», которая является собирательным названием для полного набора корней, включающих и золотое сечение. Поясним на примерах: золотое сечение – это средняя пропорция между 1 и 2, серебряное – между 2 и 3, и так вплоть до фермического (химический элемент с порядковым номером 100 в таблице Менделеева) и даже дальше.

Как мы уже говорили, золотое сечение тесно связано с эстетикой и красотой, поэтому активно используется всеми деятелями искусства – от дизайнеров интерьера до кинематографистов. Также не стоит забывать, что «золотая пропорция» переплетается со знаменитой последовательностью Фибоначчи (1, 1, 2, 3, . ), в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее равно сумме двух предыдущих чисел.

Таким образом, соотношение прогрессивных членов последовательности приближается к золотому сечению. Математики из Сингапура утверждают, что и у серебряного сечения есть собственный ряд чисел, называемый последовательностью Пелля. Фактически, можно сказать, что каждая последующая «металлическая пропорция» в свою очередь имеет собственную последовательность с соответствующими математическими закономерностями.

Точно так же, как логарифмическую спираль связывают с золотым сечением, для других металлов тоже существуют свои аналоги. Например, используя «золотое» соотношение, вы рисуете прямоугольник, затем вычеркиваете квадрат со сторонами, равными короткой стороне исходной фигуры. Оставшуюся часть вы поворачиваете на 90 градусов и получаете новый прямоугольник для деления в соответствии с «золотой пропорцией».

И так далее до самой бесконечности. Этот же прямоугольник можно разделить и с помощью других «металлических» соотношений. В каждом из случаев вы вычеркиваете необходимое количество квадратов в соответствии со значениями «металлической пропорции». Например, деля прямоугольник с помощью серебряного сечения, вы вычеркиваете два квадрата и получаете новый, уменьшенный по «серебряной» пропорции прямоугольник.

На данный момент золотое сечение является наиболее известной и широко используемой закономерностью. Однако мы не можем отрицать тот факт, что явления, связанные с «золотой пропорцией», масштабируются и по другим металлическим соотношениям. Нужно лишь немного времени на более тщательное изучение и огласку, и весь мир заговорит и о других «металлах».

Видео:Золотой треугольник, серебряный треугольникСкачать

Исследование золотых фигур

Разделы: Математика

«Хороший учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам».
Д. Пойа

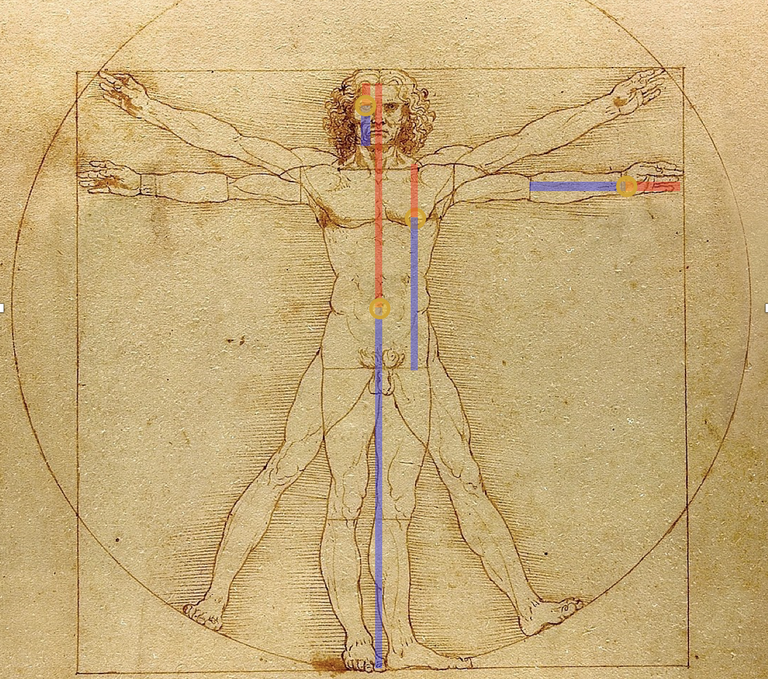
В жизни каждого человека присутствует математика. Она используется в самых разнообразных профессиях – математика нужна инженеру, военному, биологу, художнику, можно сказать, что она нужна всем. Великий художник Леонардо да Винчи был один из тех, кто заинтересовался знаменитым золотым сечением. Он много внимания уделял изучению золотого деления. Производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении; поэтому он дал этому делению название золотое сечение.

Золотое сечение интересно тем, что оно позволяет показать связь математики с другими науками, с искусством. А также помогает исследовать золотой треугольник и золотую пирамиду; рассмотреть геометрические задачи, связанные с золотыми фигурами.

Золотое сечение – это деление отрезка на две части. Таким образом, что большая его часть относится к меньшей части как весь отрезок относится к большой части.

Рис. 1.

= или , откуда

Иногда золотым сечением называют отношение, к , которое обозначают буквой φ:

Число, обратное φ обозначают Ф:

Ф=

Отметим некоторые равенства, связывающие Ф и φ , которые нам впоследствии пригодятся:

1-Ф, 1+Ф=

История золотого сечения.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне и они были известны только посвященным.

Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».

ЗОЛОТОЙ ПРЯМОУГОЛЬНИК.

Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении.

Чтобы убедиться в этом, заметим, что по теореме Пифагора

Прямоугольник АЕFD со сторонами АЕ=φАD называется золотым прямоугольником. Четырехугольник АВСD − квадрат. Нетрудно видеть, что прямоугольник ВЕFС также золотой, поскольку BC=a=φВЕ. Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕFС.

Можно ли считать, что прямоугольник с отношением сторон, равным φ, выглядит изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 или 5:7? Чтобы ответить на этот вопрос, были проведены специальные эксперименты. Результаты их не вполне убедительны, но все же свидетельствуют о некотором предпочтении, отдаваемом золотому сечению.

ЗОЛОТОЙ ТРЕУГОЛЬНИК И ЕГО ИССЛЕДОВАНИЕ.

Золотым треугольником будем называть равнобедренный треугольник, отношение основания которого к боковой стороне равно φ Одним из таких треугольников является треугольник с боковой стороной Ф и основанием 1; именно его мы в дальнейшем будем называть золотым. Проведем исследование золотого треугольника.

Углы золотого треугольника.

В треугольнике АВС выберем на стороне ВС точку D так, чтобы АD=1 (такую точку легко построить, проведя окружность с центром в точке А и радиусом АС). Из подобия треугольников АВС и АDС получаем:

или , откуда DС=

Поскольку ВС=Ф, DС=φ, то, учитывая равенство Ф=, получаем, что BD=1 и треугольник ABD равнобедренный. Значит, АD- биссектриса треугольника АВС. Теперь легко найти углы треугольника АВС:

5,

В последствии нам встретятся выражения, содержащие и , поэтому вычислим их значения и для удобства выразим через Ф:

=.

Найдем в золотом треугольнике:

медиану, проведенную к боковой стороне;
высоту, проведенную к основанию;
площадь;
высоту, проведенную к боковой стороне;

Пусть треугольник АВС − золотой. Для нахождения медианы воспользуемся формулой ,

где

Найдем высоту ВН: ВН=Ф

Площадь треугольника АВС будет равна: S=

Пусть – высота, проведенная к стороне ВС. Возьмем на стороне ВС точку так, чтобы . Треугольники АС и АВС подобны с коэффициентом подобия Ф, поэтому

Применение золотого треугольника при решении задач.

Найти длины диагоналей правильного 10-угольника со стороной, равной 1.

Решение. Правильный 10-угольник имеет 4 вида диагоналей, на рисунке показано по одному представителю этих четырех множеств. Найдем их длины. Проще всего найти длину отрезка AF. Для этого найдем величину внутреннего угла правильного 10-угольника: . Теперь легко заметить, что 10-угольник состоит из 10 золотых треугольников, которые имеют общую вершину О ─ центр 10-угольника. Значит, длина диагонали AF равна 2Ф.

Найдем длину диагонали АС. Из треугольника АВС имеем:

= 22) =2(1+)= 4= 2+Ф,

откуда АС=

Найдем длину диагонали AD. В равнобоковой трапеции АВСD углы при основании равны Нетрудно получить, что проекции отрезков АВ и СD на основании AD будут равны .

AD=.

Длину диагонали АЕ можно найти разными способами.

Способ 1. Будем искать ее из треугольника AEF. В этом треугольнике медиана ЕО равна половине стороны AF, поэтому треугольник AEF-прямоугольный. Тогда АЕ= AF

Способ 2. Заметим, что высота золотого треугольника EOF является средней линией треугольника AEF. Поскольку эта высота равна , то АЕ=

Ответ: 2Ф, ,

ЗОЛОТАЯ ПИРАМИДА И ЕЕ ИССЛЕДОВАНИЕ.

Пирамида называется золотой, если каждая её грань − золотой треугольник.

Исследование золотой пирамиды.

Различные способы нахождения объёма золотой пирамиды.

I способ: объем пирамиды находим по формуле . Для этого нам необходимо вычислить высоту пирамиды.

Пусть DABC-данная пирамида,DH − ее высота. Плоскость ADH пересекает ребро ВС в точке М, причем ВМ=СМ. Треугольник ADM − равнобедренный.

Опустим на его основание AD высоту МК. Из подобия треугольников AHD и AKM будем иметь:

.

Поставим в это равенство известные нам числа:

МК= (расстояние между ребрами AD и ВС),

АМ= (высота золотого треугольника):

DH=. А т.к. =.

II способ:

длины противоположных ребер, расстояние между ними, – угол между ними;

III способ:

Объем золотой пирамиды – это объем прямоугольного параллелепипеда минус объем четырех маленьких пирамид с ребрами длиной 1,, и , значит:

Применение золотой пирамиды при решении задач.

Найдем площадь поверхности золотой пирамиды.

= = 4

Золотое сечение в картине Леонардо да Винчи «Джоконда»

Портрет Моны Лизы привлекает тем, что композиция рисунка построена на»золотых треугольниках» (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).

Золотая спираль в картине Рафаэля «Избиение младенцев»

В отличии от золотого сечения ощущение динамики, волнения проявляется, пожалуй, сильней всего в другой простой геометрической фигуре – спирали. Многофигурная композиция, выполненная в 1509 – 1510 годах Рафаэлем, когда прославленный живописец создавал свои фрески в Ватикане, как раз отличается динамизмом и драматизмом сюжета. Рафаэль так и не довел свой замысел до завершения, однако, его эскиз был гравирован неизвестным итальянским графиком Маркантинио Раймонди, который на основе этого эскиза и создал гравюру» Избиение младенцев». На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции −точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, − вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Если естественным образом соединить эти куски кривой пунктиром, то с очень большой точностью получается . золотая спираль! Это можно проверить, измеряя отношение длин отрезков, высекаемых спиралью на прямых, проходящих через начало кривой.

Мы не знаем, рисовал ли на самом деле Рафаэль золотую спираль при создании композиции » Избиение младенцев» или только»чувствовал» её. Однако с уверенностью можно сказать, что гравер Раймонди эту спираль увидел.

Об этом свидетельствуют добавленные им новые элементы композиции, подчеркивающие разворот спирали в тех местах, где она у нас обозначена лишь пунктиром. Эти элементы можно увидеть на окончательной гравюре Раймонди: арка моста, идущая от головы женщины, − в левой части композиции и лежащее тело ребенка − в ее центре.

Нельзя не увидеть золотой треугольник и золотую пирамиду в ограненных драгоценных камнях. Многие гранильщики стараются придать бриллиантам форму тетраэдра, куба, октаэдра или икосаэдра. Но эти замечательные тела еще и потому красивы, что в основе их пропорциональных линий лежит золотая пропорция. Многие материалы, и не только драгоценные камни, состоят из мельчайших частиц, которые имеют форму многогранника. Такие вещества называются кристаллами. Соль, лед, песок, графит и т. д. состоят из кристаллов. Внутреннее устройство кристалла представляется в виде кристаллической решетки, в ячейках которых размещены по законам симметрии одинаковые мельчайшие частицы.

Литература: