Дан куб abcda1b1c1d1 указать скрещивающиеся прямые с прямой вс указать прямые параллельные прямой

Геометрия | 10 — 11 классы

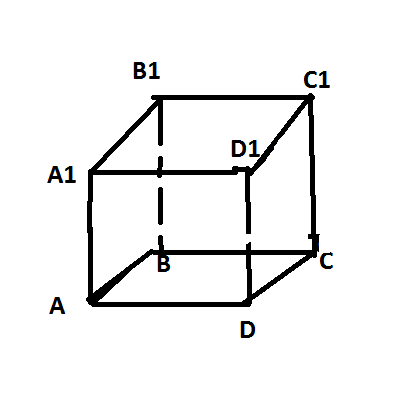
Дан куб ABCDA1B1C1D1 Укажите в кубе : 1 — прямую, скрещивающуюся с прямой BC, в каких параллельных плоскостях они лежат?

, скрещивающуюся с прямой А1С1 : найдите расстояние между ними Буквы именно в таком порядке.

1) AA1 (плоскость AA1D1D) иBC (плоскость BB1C1C) ;

DD1 (плоскость AA1D1D) иBC (плоскость BB1C1C) ;

2) BD (плоскость ABCD)иA1C1 ().

Пусть точка О — середина отрезка BD, а точка О1 — середина отрезка A1C1⇒ Расстояние между прямыми — это отрезок ОО1.

Видео:7. Скрещивающиеся прямыеСкачать

Точки A, B, C, D не лежат в одной плоскости?

Точки A, B, C, D не лежат в одной плоскости.

Среди прямых, проходящих через любые из двух данных точек, укажите прямую которая является скрещивающей.

A)с прямой AB ; b)с прямой BC.

Видео:10 класс - Геометрия - Скрещивающиеся прямыеСкачать

Прямые a и b лежат в параллельных плоскостях альфа и бета?

Прямые a и b лежат в параллельных плоскостях альфа и бета.

Могут ли эти прямые быть : а)параллельными ; б) скрещивающимися?

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

«дан куб ABCDA1B1C1D1?

«дан куб ABCDA1B1C1D1.

Укажите три прямые, проходящие : а) через точку D и скрещивающиеся с прямой AB1, б) через точку B1 и скрещивающиеся с прямой A1D.

Видео:Стереометрия для ЕГЭ: 2 - параллельные и скрещивающиеся прямыеСкачать

Помогите с задачками , не сложные ?

Помогите с задачками , не сложные .

1 В тетраэдре ABCD , укажите прямую , скрещивающуюся с прямой AB .

2 В кубе ABCD A1B1C1D1 в плоскости ABCD найдите прямые , паралельные прямой A1B1 .

3 В кубе ABCD A1B1C1D1 найдите угол между скрещивающимися прямыми AA1 и ВВ1.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

АВСДА1В1С1Д1 куб?

Найдите угол между скрещивающимися прямыми АД1 и В1С.

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Прямые А и В лежат в параллельных плоскостях а и б?

Прямые А и В лежат в параллельных плоскостях а и б.

Могут ли эти прямые быть параллельными, скрещивающимися.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Дано 2 скрещивающиеся прямые а и б сколько существует разных плоскостей которые проходят через прямую а и параллельны прямой б?

Дано 2 скрещивающиеся прямые а и б сколько существует разных плоскостей которые проходят через прямую а и параллельны прямой б.

Видео:№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать

Даны две скрещивающиеся прямые?

Даны две скрещивающиеся прямые.

Через одну из них проведите плоскость, параллельную другой.

Видео:Параллельность прямых. 10 класс.Скачать

На модели куба укажите ребра куба находящиеся на скрещивающихся прямых?

На модели куба укажите ребра куба находящиеся на скрещивающихся прямых.

Видео:Параллельность прямых. Практическая часть. 10 класс.Скачать

Прямые a и b лежат в параллельных плоскостях альфа и бета?

Прямые a и b лежат в параллельных плоскостях альфа и бета.

Могут ли эти прямые быть : а)параллельными ; б)скрещивающимися?

Вопрос Дан куб ABCDA1B1C1D1 Укажите в кубе : 1 — прямую, скрещивающуюся с прямой BC, в каких параллельных плоскостях они лежат?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 10 — 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

296. а) А = 85 и В = 95 градусов. Б) А = 45 и В = 135 градусов. 308. (см) (см).

Центр описанной около прямоугольного треугольника окружности — середина гипотенузы))) т. К. боковые ребра пирамиды равны, следовательно, и их проекции равны, т. Е. основание высоты пирамиды — середина гипотенузы))) осталось построить линейный угол ..

В треугольнике АВС угол С = 30°, АС = 10 см, ВС = 8 см. Через вершину А проведена прямая а, параллельная ВС. Найдите : а) расстояние от точки В до прямой АС ; б) расстояние между прямыми а и ВС. А) Расстояние от точки до прямой ― это длина перпенд..

Вопрос не точен. Но ето утверждение не верно.

Добрый день! Я рада Вам помочь! Решение задачи во вложенном файле.

V = 1 / 3 * Sосн. * H = 1 / 3 * 3 * 10 * 5 = 50(cм³).

ЕО = √145 см, АВ = 24 см. ОМ⊥АВ. ОМ = АВ / 2 = 12 см. В прямоугольном тр — ке ЕМО ЕМ² = ЕО² + ОМ² = 145 + 12² = 289, ЕМ = 17 см. Площадь боковой поверхности : Sб = р·l, где р — полупериметр основания, l — апофема. Sб = 3·АВ·ЕМ / 2 = 3·24·17 / 2 ..

Ответ : |Am = √13 ед. |АС| = 5 ед. Объяснение : Вектор Am равен сумме векторов АВ и Вm. Вектор AС равен сумме векторов АВ и ВС. Модуль суммы двух векторов можно вычислить, используя теорему косинусов : |Аm|² = |AB|² + |Bm|² + 2 * |AB| * |Bm| * Co..

4х + х + х = 180 градусов х = 30 градусов углы : 30 30 и 120 медиана = боковая сторона синуса синус а = 30 градусов — а это 0. 5 6 = х * 0. 5 х = 12 ответ : 12см.

Свойство вн. Угла это сумма двух углов ∆ не смежные с ним. Поэтому 47 + 72 = 119.

Видео:Скрещивающиеся прямыеСкачать

Школе NET

Register

Do you already have an account? Login

Login

Don’t you have an account yet? Register

Newsletter

Submit to our newsletter to receive exclusive stories delivered to you inbox!

• Главная 
• Вопросы & Ответы 
• Вопрос 12075926

Суррикат Мими

Видео:№194. Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащимиСкачать

выполните чертёж куба ABCDA1B1C1D1по чертежу укажите а)прямые параллельные для прямой AD б) прямые скрещивающие с прямой cc1 в) плоскости параллельные прямой AB

Видео:№39. Докажите, что если АВ и CD скрещивающиеся прямые, то AD и ВС также скрещивающиеся прямые.Скачать

РАССТОЯНИЕ И УГОЛ МЕЖДУ СКРЕЩИВАЮЩИМСЯ ПРЯМЫМИ (РЕШЕНИЕ ЗАДАЧ ГРУППЫ С 2 ЕГЭ) — презентация

Презентация была опубликована 6 лет назад пользователемПётр Красинский

Похожие презентации

Видео:№191. Дан куб ABCDA1B1C1D1. Докажите, что плоскостиСкачать

Презентация по предмету «ЕГЭ» на тему: «РАССТОЯНИЕ И УГОЛ МЕЖДУ СКРЕЩИВАЮЩИМСЯ ПРЯМЫМИ (РЕШЕНИЕ ЗАДАЧ ГРУППЫ С 2 ЕГЭ)». Скачать бесплатно и без регистрации. — Транскрипт:

1 РАССТОЯНИЕ И УГОЛ МЕЖДУ СКРЕЩИВАЮЩИМСЯ ПРЯМЫМИ (РЕШЕНИЕ ЗАДАЧ ГРУППЫ С2 ЕГЭ)

2 Основные принципы построения изображения пространственной фигуры выбор оптимального положения изображаемого тела; выбор ракурса и проекции, умение минимизировать количество изображенных линий (видимые и невидимые линии должны изображаться различным образом); умение строить сечения и проекции на плоскость; умение выделить на построенном чертеже и соответственно изобразить плоскую конфигурацию, дающую ключ к решению задачи.

3 Первый способ сводится к нахождению расстояния от точки до плоскости Идея заключается в построении: а) двух параллельных плоскостей, каждая из которых проходит через одну из скрещивающихся прямых, параллельно другой скрещивающейся прямой. Расстояние между этими плоскостями будет искомым. б) в построении плоскости, проходящей через одну из скрещивающихся прямых, параллельно другой. Расстояние от любой точки второй прямой до построенной плоскости будет искомым. Расстояние между скрещивающимся прямыми

4 Если одна из двух данных прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью. Расстояние между скрещивающимся прямыми

5 Задача 1. В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 с высотой Н и стороной основания а, найти расстояние между прямыми АА 1 и ЕD 1. Расстояние между скрещивающимся прямыми

6 З а д а ч а 2. В основании прямой призмы АВСА 1 В 1 С 1 лежит правильный треугольник со стороной а. Боковое ребро призмы равно 2 а. Точка Р — середина ребра ВВ 1, R — середина СС 1. Найдите расстояние между прямыми AR и СР. Расстояние между скрещивающимся прямыми

7 Задача 3. Основание прямого параллелепипеда ABCDA 1 B 1 C 1 D 1 – квадрат со стороной а, боковое ребро равно b. Найти расстояние между прямыми АВ 1 и ВD.

8 УГОЛ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения. Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.

9 Задача 4. В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 с высотой h и стороной основания а, найти угол между прямыми АА 1 и ЕD 1. Угол между скрещивающимся прямыми Поэтапно-вычислительный метод

10 Задача 5. В правильной шестиугольной призме АBCDEFA 1 B 1 C 1 D 1 E 1 F 1, все ребра которой равны 1, найдите угол между прямыми АВ 1 и СD 1. Угол между скрещивающимся прямыми Поэтапно-вычислительный метод

11 Задача 6. В правильной треугольной призме АВСА 1 В 1 С 1, ребра которой равны 1, найдите угол между прямыми АС 1 и В 1 С. Угол между скрещивающимся прямыми Поэтапно-вычислительный метод

12 Координатно-векторный метод вычисления углов между скрещивающимися прямыми При нахождении угла φ между прямыми а и b используют формулу или в координатной форме:, где и — векторы, параллельные прямым а и b. В частности, если прямые а и b перпендикулярны, то и

13 Задача 7. В единичном кубе АBCDA 1 B 1 C 1 D 1 найдите угол между прямыми АЕ и DF, где Е и F – точки, расположенные на ребрах CD и C 1 D 1 так, что Угол между скрещивающимся прямыми координатно-векторный метод

14 Задача 8. В правильной шестиугольной призме АBCDEFA 1 B 1 C 1 D 1 E 1 F 1,все ребра которой равны 1, найдите угол между прямыми АВ 1 и ВЕ 1. Угол между скрещивающимся прямыми

17 Нахождение расстояния и угла между скрещивающимися прямыми на основе метода ортогонального проектирования. Расстояние между скрещивающимися прямыми от точки, являющейся проекцией одной из данных прямых на перпендикулярную ей плоскость, до проекции другой прямой на эту плоскость. Угол между второй прямой и указанной ей проекцией дополняет до 90° угол между данными скрещивающимися прямыми.

18 Если ортогональная проекция на плоскость переводит прямую a в точку A, а прямую b в прямую b, то расстояние AB между прямыми a и b равно расстоянию AB от точки A до прямой B.

19 Ортогональное проектирование – это проектирование вдоль прямой, перпендикулярной плоскости проекции. Свойства ортогонального проектирования: 1. Проекцией фигуры, лежащей на плоскости проекции, является сама эта фигура. 2. Проекцией прямой (отрезка) является прямая (отрезок). 3. Отношение длин параллельных отрезков равно отношению длин их проекций. 4. Площадь ортогональной проекции многоугольника равна площади этого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекции: Sпр = Scosφ.

20 Задача 9. Сторона основания правильной четырехугольной призмы равна 15, высота равна 20. Найдите кратчайшее расстояние от стороны основания до не пересекающей ее диагонали призмы.

21 Задача 10. Дан куб ABCDA 1 B 1 C 1 D 1 с ребром а. Точка К — середина ВС. Найдите расстояние между прямыми АС и С 1 К.

22 Задача 11. Найти расстояние между скрещивающимися диагоналями соседних граней куба с ребром 1.

23 Задача 12. В основании пирамиды SАВС лежит равносторонний треугольник АВС, длина стороны которого равна. Боковое ребро перпендикулярно плоскости основания и имеет длину 2. Найти величину угла и расстояние между скрещивающимися прямыми, одна из которых проходит через точку S и середину ребра ВС, а другая – через точку С и середину ребра АВ.

24 Задача 13. В правильной треугольной призме АВСА 1 В 1 С 1, все ребра которой равны 1, найдите расстояние между прямыми АВ и СВ 1.

25 Задача 14. В правильной четырехугольной пирамиде SАВСD, все ребра которой равны 1, найдите расстояние между прямыми SB и AD.

26 Задача 15. В пирамиде DABC известны длины ребер DB= 8, AC = 24, АВ = ВС = DA = DC = 13. Найдите расстояние между прямыми DB и АС.

27 Задача 16. К диагонали А 1 С куба АВСDA 1 B 1 C 1 D 1 провели перпендикуляры из вершин А и В. Найдите угол между этими перпендикулярами.

28 Задача 17. К диагонали А 1 С куба АВСDA 1 B 1 C 1 D 1 провели перпендикуляры из середин ребер АВ и АD. Найдите угол между этими перпендикулярами.

29 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и B 1 C 1.

30 Ответ:. Решение. Продолжим стороны B 1 C 1 и A 1 F 1 до пересечения в точке G. Треугольник A 1 B 1 G равносторонний. Его высота A 1 H является искомым общим перпендикуляром, длина которого равна.

31 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и C 1 D 1.

32 Ответ:. Решение. Искомым общим перпендикуляром является отрезок A 1 C 1. Его длина.

33 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BC 1.

34 Ответ:. Решение. Искомым расстоянием является расстояние между параллельными плоскостями ADD 1 и BCC 1. Расстояние между ними равно.

35 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CD 1.

36 Ответ:. Решение. Искомым общим перпендикуляром является отрезок AC. Его длина равна.

37 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и DE 1.

38 Ответ:. Решение. Искомым общим перпендикуляром является отрезок A 1 E 1. Его длина равна.

39 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BD 1. Решение. Искомым общим перпендикуляром является отрезок AB. Его длина равна 1. Ответ: 1.

40 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CE 1.

41 Ответ:. Решение. Искомым расстоянием является расстояние между прямой AA 1 и плоскостью CEE 1. Оно равно.

42 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BE 1.

43 Ответ:. Решение. Искомым расстоянием является расстояние между прямой AA 1 и плоскостью BEE 1. Оно равно.

44 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CF 1.

45 Ответ:. Решение. Искомым расстоянием является расстояние между прямой AA 1 и плоскостью CFF 1. Оно равно.

46 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите угол между прямыми: AB 1 и DE 1. Ответ:. Решение. Искомым расстоянием является расстояние между параллельными плоскостями ABB 1 и DEE 1. Расстояние между ними равно.

47 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите угол между прямыми: AB 1 и CF 1.

48 Ответ: Решение. Искомым расстоянием является расстояние между прямой AB 1 и плоскостью CFF 1. Оно равно.

49 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите угол между прямыми: AB 1 и BC 1.

50 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BC 1. Решение. Пусть O, O 1 –центры граней призмы. Плоскости AB 1 O 1 и BC 1 O параллельны. Плоскость ACC 1 A 1 перпендикулярна этим плоскостям. Искомое расстояние d равно расстоянию между прямыми AG 1 и GC 1. В параллелограмме AGC 1 G 1 имеем AG = ; AG 1 =. Высота, проведенная к стороне AA 1 равна 1. Следовательно, d =. Ответ:

51 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BD 1.

52 Решение. Рассмотрим плоскость A 1 B 1 HG, перпендикулярную BD 1. Ортогональная проекция на эту плоскость переводит прямую BD 1 в точку H, а прямую AB 1 – в прямую GB 1. Следовательно искомое расстояние d равно расстоянию от точки H до прямой GB 1. В прямоугольном треугольнике GHB 1 имеем GH = 1; B 1 H =.Следовательно, d =. Ответ:

53 В правильной 6-й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BE 1.

54 Решение. Рассмотрим плоскость A 1 BDE 1, перпендикулярную AB 1. Ортогональная проекция на эту плоскость переводит прямую AB 1 в точку G, а прямую BE 1 оставляет на месте. Следовательно искомое расстояние d равно расстоянию GH от точки G до прямой BE 1. В прямоугольном треугольнике A 1 BE 1 имеем A 1 B = ; A 1 E 1 =. Следовательно, d =. Ответ:

💥 Видео

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

№36. Прямая с пересекает прямую а и не пересекает прямую b, параллельную прямой а.Скачать

Стереометрия 10 класс. Часть 2 | Математика | TutorOnlineСкачать

Готовимся к ЕГЭ. Стереометрия. Базовые задачи. Угол между прямыми. КубСкачать

В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и В1D1. Ответ дайте в градусах.Скачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать