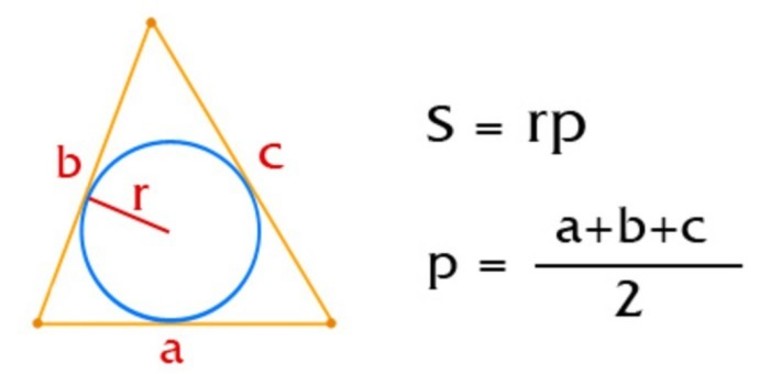- Фигура с тремя сторонами
- Вписанный в окружность треугольник
- Пересечение медиатрис
- Типы фигур и точка O
- Формулы для определения площади
- Решение задач
- Формулы для вычисления площадей различных треугольников. 10-й класс
- Презентация к уроку
- I. Организационная часть:
- II. Повторение материала, решение задач, знакомство с новыми формулами.
- III. Домашнее задание. Приложение 2.
- IV. Итог урока.
- Как найти площадь треугольника
- Основные понятия
- Формула площади треугольника
- Общая формула
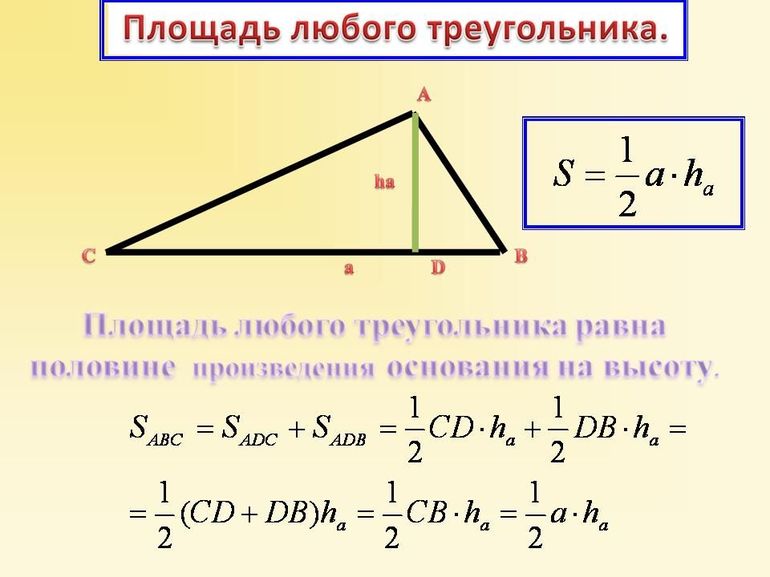
- 1. Площадь треугольника через основание и высоту
- 2. Площадь треугольника через две стороны и угол между ними
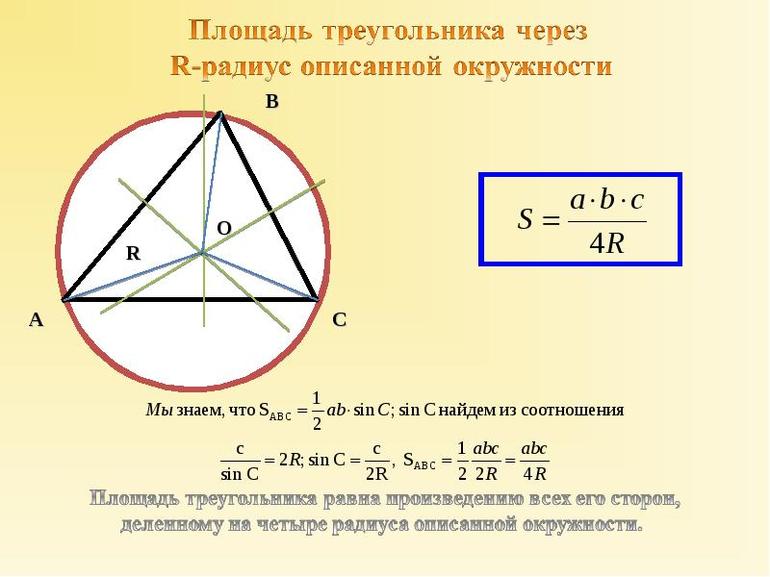
- 3. Площадь треугольника через описанную окружность и стороны
- 4. Площадь треугольника через вписанную окружность и стороны
- 5. Площадь треугольника по стороне и двум прилежащим углам
- 6. Формула Герона для вычисления площади треугольника
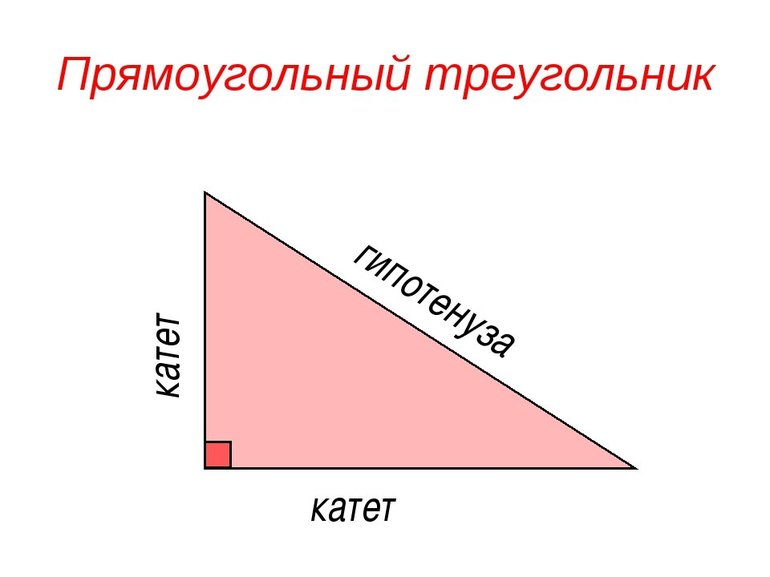
- Для прямоугольного треугольника
- Площадь треугольника с углом 90° по двум сторонам
- Площадь треугольника по гипотенузе и острому углу
- Площадь прямоугольного треугольника по катету и прилежащему углу
- Площадь треугольника через гипотенузу и радиус вписанной окружности
- Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
- Площадь прямоугольного треугольника по формуле Герона
- Для равнобедренного треугольника
- Вычисление площади через основание и высоту
- Поиск площади через боковые стороны и угол между ними
- Площадь равностороннего треугольника через радиус описанной окружности
- Площадь равностороннего треугольника через радиус вписанной окружности
- Площадь равностороннего треугольника через сторону
- Площадь равностороннего треугольника через высоту
- Таблица формул нахождения площади треугольника
- 💥 Видео
Видео:Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Фигура с тремя сторонами
Чтобы понять, как рассчитывать площадь треугольника, вписанного в окружность, необходимо иметь четкое представление о рассматриваемой фигуре. Каждый школьник знает о геометрическом объекте, который ограничен тремя отрезками. Основными элементами треугольника являются следующие:
- Стороны, которых у фигуры три. Они могут быть равны по длине или отличаться друг от друга. При этом всегда справедливым остается тот факт, что длина любой стороны меньше суммы длин двух других.
- Вершины — это три точки, которые образованы на пересечении соответствующих сторон. Каждая из них характеризуется определенным значением угла. Для трех углов треугольника справедливо следующее равенство: ∠A + ∠B + ∠C = 180 °, где латинскими буквами названы соответствующие вершины.
Помимо вершин и сторон, треугольник характеризуется дополнительными отрезками, которые часто используются для доказательства теорем и решения геометрических задач. К имеющим специальное название отрезкам относятся такие:
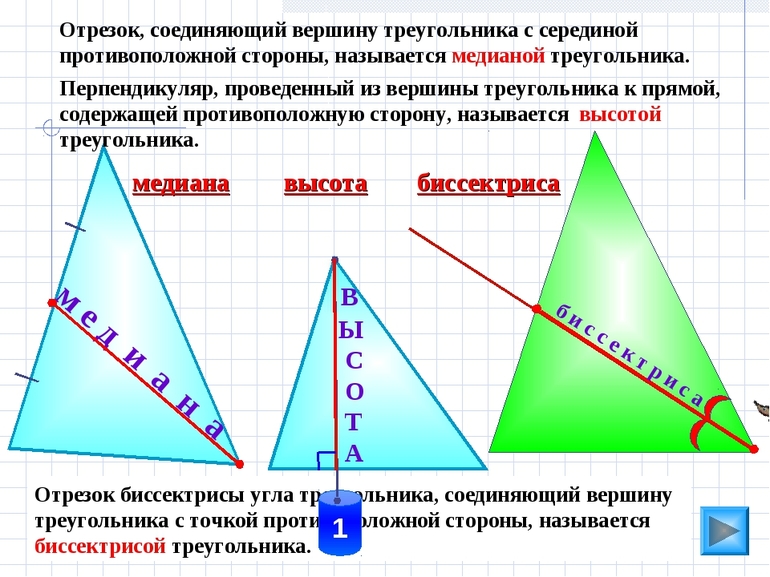
- Медиана — делящий треугольник на две фигуры с одинаковой площадью отрезок. Он проходит через вершину и середину противоположной стороны. Все три медианы пересекаются в одной точке, которая является массовым центром рассматриваемого геометрического объекта.
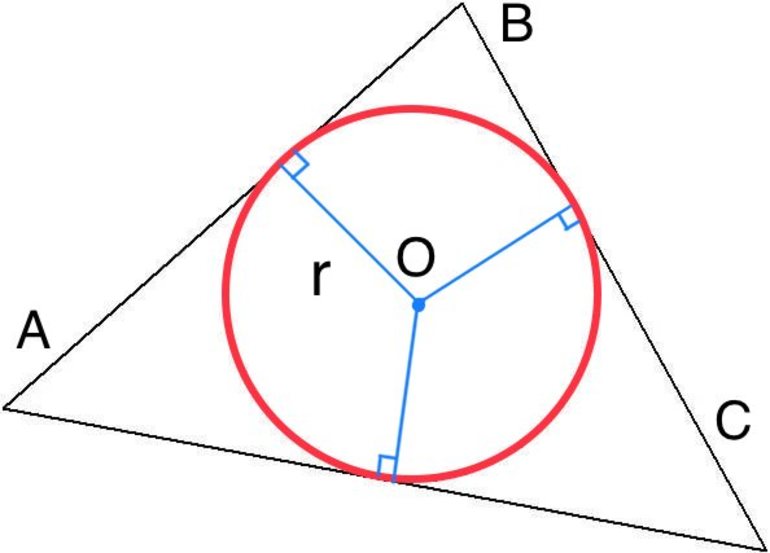
- Биссектриса — отрезок, который делит пополам угол при вершине. Все три биссектрисы, как и медианы, пересекаются в одной точке, которая является центром вписанной в треугольник окружности.
- Высота — перпендикуляр, который через вершину опускается на противоположную сторону. Высоты часто используются при вычислении площадей.
- Средняя линия — проходящая через середины двух сторон линия, которая является параллельной третьей. Обе стороны отсекают отрезок, длина которого составляет половину от длины противоположной стороны.
- Медиатриса или серединный перпендикуляр — это прямая линия, которая пересекает под углом 90 ° сторону треугольника. Важным свойством медиатрис является тот факт, что точка из пересечения — это центр описанной вокруг фигуры окружности.
Видео:Площадь треугольника через радиус описанной окружности: ОГЭ - ЕГЭСкачать

Вписанный в окружность треугольник
Чтобы уметь вычислять площадь описанного треугольника, следует понимать, о каком взаимном расположении многоугольника и окружности идет речь. Согласно определению, если через все вершины полигона проходит окружность, значит, он считается вписанным в нее. Это простое определение не всегда выполняется для произвольного многоугольника, однако, для любой правильной фигуры оно будет справедливым, например, для квадрата или прямоугольника.
Касательно треугольника следует отметить, что он является единственным многоугольником, для которого всегда можно найти центр и радиус описывающей его окружности. Причем независимо от того, какой тип фигуры рассматривается.
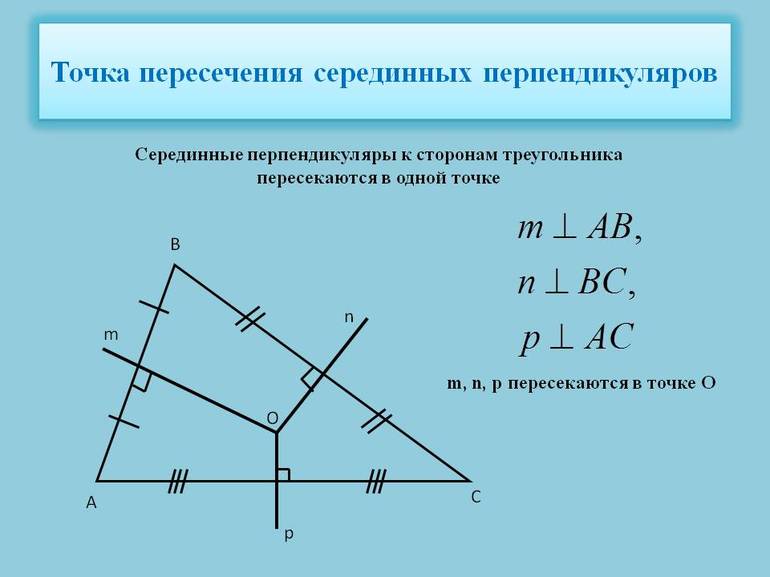
Пересечение медиатрис
В рассматриваемой фигуре имеется три разных медиатрисы. Каждую из них построить несложно для любой из сторон. Для построения следует выполнить последовательность действий:
- Выбрать сторону.
- Установить циркуль в один из концов стороны и провести дугу окружности, которая будет пересекать сторону дальше, чем посередине.
- Пункт 2 выполнить, установив циркуль во второй конец стороны.
- Соединить точки пересечения дуг в одну линию. Она является медиатрисой.
Из проделанных построений следует один важный факт для всех треугольников: точка пересечения их медиатрис является центром описывающей фигуру окружности. Доказать это утверждение легко. Например, имеется треугольник ABC. Пусть проведена медиатриса m к стороне AB. Любая из точек, принадлежащих прямой m, находится на одинаковом расстоянии от вершин A и B.
Пусть проведена еще одна медиатриса n к стороне BC. Прямые m и n пересекаются в точке O. Поскольку O принадлежит обеим медиатрисам, то она, с одной стороны, находится на одном расстоянии от A и B, с другой стороны, она находится на одинаковой дистанции от вершин B и C. Этот факт дает право сделать вывод о том, что расстояния OA, OB и OC равны. Если их обозначить буквой R, то можно говорить, что R — радиус окружности с центром в точке O, которая проходит через три вершины треугольника, то есть описывается его.
Очевидно, что третья медиатриса также пройдет через O. В противном случае будут существовать три разные точки, которые одновременно будут находиться на одинаковом расстоянии от трех вершин треугольника и будут лежать в одной плоскости с ним, а это невозможно из свойств двумерного пространства.
Типы фигур и точка O
Поскольку для треугольника любого типа можно провести описывающую его окружность, то представляет интерес рассмотреть вопрос положения ее центра O. В общем случае существуют три типа рассматриваемого многоугольника:
- С острыми углами, то есть все они менее 90 °. К этим треугольникам относятся равносторонние. Для них центр описанной окружности всегда расположен внутри фигуры.
- С одним тупым углом и двумя острыми. Это может быть либо равнобедренный треугольник, либо фигура общего типа. Для нее точка O всегда расположена вне области, ограниченной сторонами многоугольника, то есть за его пределами.
- Прямоугольный. Для такого типа треугольников центр описанной окружности расположен точно посередине гипотенузы. Это свойство треугольника, которое доказывается просто, если рассмотреть точку пересечения двух средних линий, проведенных относительно катетов. Поскольку O лежит посередине гипотенузы, то последняя является диаметром описанной окружности. Любой треугольник, который опирается на диаметр одной из своих сторон, и третья вершина которого лежит на окружности, является прямоугольным.
Очевидно, что если треугольник является полностью вырожденным, то провести описывающую его окружность нельзя, поскольку такая фигура обращается в прямой отрезок.
Формулы для определения площади
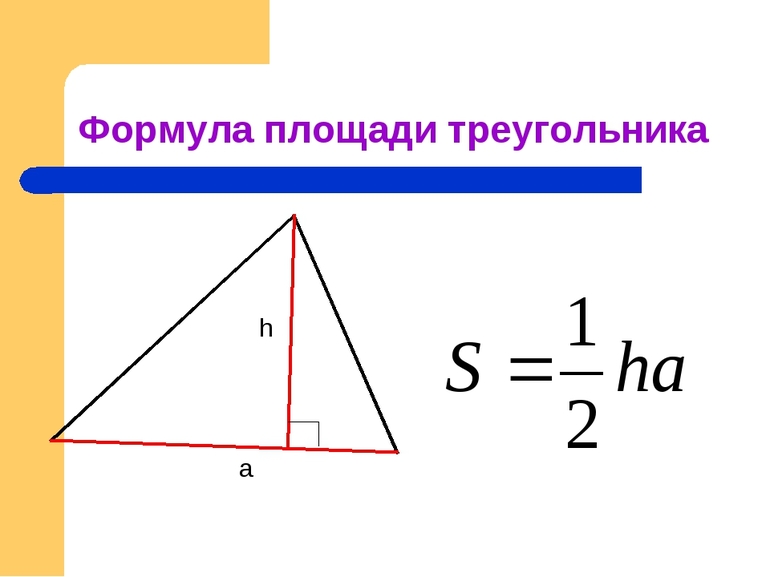
Как известно, площадь треугольника произвольного типа может быть рассчитана, как половина произведения высоты h на длину основания a: S = ½*h*a. Существует также еще одно универсальное выражение для определения S — это половина модуля векторного произведения направляющих отрезков, образующих любые две стороны.
Что касается формул площади треугольника, описанного около окружности, то нужно отметить, что известны несколько из них. Соответствующие равенства имеют следующий вид:
Где a, b, c — длины соответствующих сторон треугольника, ha, hb, hc — высоты, проведенные к a, b и c, соответственно. Видно, что все три формулы требуют знание минимум 4 параметров для рассматриваемой фигуры (радиус и три высоты или три длины сторон).
Полезно также привести формулу для расчета радиуса R:
Здесь p = (a+b+c)/2 — полупериметр треугольника. Следует отметить, что знаменатель в выражении для радиуса является не чем иным, как формулой Герона для расчета площади S фигуры.
Видео:Задание 24 Площадь описанного треугольникаСкачать

Решение задач
Как правило, прямое использование формул площади треугольника через окружность описанную является невозможным для типичных геометрических задач. Для их решения необходимо внимательно проанализировать условие и использовать все имеющиеся знания для определения неизвестных в выражениях для S через R.
Для некоторых задач может потребоваться использование уравнений прямых, которые на плоскости в векторной форме имеют вид:
(x, y) = (x0, y0) + α*(v1, v2).
Здесь (x, y) и (x0, y0) — координаты произвольной и известной точек прямой, соответственно, (v1, v2) — координаты направляющего вектора, α — числовой параметр.
Для закрепления полученных знаний полезно решить одну простую задачу. Известно, что один из острых углов в прямоугольном треугольнике составляет 30 °. Чему равна площадь этой фигуры, если радиус описанной окружности для нее составляет 12 см.
Для решения задачи воспользуемся следующим выражением через радиус окружности, описанной около треугольника, для площади:
Пусть c — это гипотенуза, тогда c = 2*R = 24 см. Катеты a и b можно связать с гипотенузой функциями синуса и косинуса:
- a = c*cos (α) = 24*3 0,5 /2 = 20,7846 см;
- b = c*sin (α) = 24*½ = 12 см.
Подставляя полученные значения в формулу для S через R, можно получить ответ:
S = a*b*c/(4*R) = 20,7846*12*24/(4*12) ≈ 124,71 см 2 .
Важно понимать, что формулы расчета площади рассматриваемого многоугольника через радиус описанной окружности используются редко, поскольку они могут быть заменены аналогичными более простыми выражениями, как в случае с высотой и основанием. В решенной задаче, например, можно было не применять указанную для S формулу, а просто рассчитать полупроизведение катетов:
S = ½*a*b = ½*20,7846*12 ≈ 124,71 см 2 .
Таким образом, вокруг каждого треугольника можно описать окружность радиуса R, центр которой расположен в точке пересечения его серединных перпендикуляров (медиатрис). Существует несколько формул для вычисления площади фигуры через радиус R, однако, все они требуют знания либо сторон, либо высот треугольника, и в большинстве случаев могут быть заменены более простыми выражениями при решении задач.
Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Формулы для вычисления площадей различных треугольников. 10-й класс
Класс: 10
Презентация к уроку
Цель урока:
- Образовательная цель: обеспечить в ходе урока сознательное повторение формул для вычисления площади треугольника, которые изучаются в школьной программе. Показать необходимость знания II формулы Герона, формулы площади треугольника, заданного в прямоугольной системе координат. Обеспечить сознательное усвоение и применение этих формул при решении задач. Показать формулу площади треугольника через радиусы вписанной и вневписанных окружностей. Учиться получать следствия из формул и показать это на некоторых выводах.
- Воспитательная цель: воспитывать сознательное отношение к учебе повышение интереса к математике, к истории математики, к научно-исследовательской работе.
- Развивающая цель: развивать логическое мышление, математическую речь. умение сравнивать и делать выводы; совершенствовать навыки работы с формулами, учиться получать из них следствия.
Методы и приёмы: словесный и наглядный.
По типу: урок обобщения и систематизации знаний.
Наглядность к уроку и раздаточный материал:
- презентация;
- памятки с рисунками, где учащиеся будут записывать формулы (приложение 1);
- задания для практической работы (приложение 2);
- учебник.
Ход урока
I. Организационная часть:
- Приветствие.
- Подготовка учащихся к уроку.
- Получение сведений об отсутствующих.
II. Повторение материала, решение задач, знакомство с новыми формулами.
Сегодня у нас обобщающий урок повторения по теме «Формулы для вычисления площадей различных треугольников». Зная формулы для вычисления площади треугольника, можно посчитать площадь любого многоугольника, предварительно разбив его на треугольники. Эта тема является одной из важнейших тем геометрии.
Мы повторим те формулы, которые вы знаете. Я вам покажу ещё несколько формул, знать которые необходимо для успешной сдачи ЕГЭ. И применим эти формулы при решении задач.
Запишите тему урока. Прежде чем приступить непосредственно к формулам давайте вспомним две теоремы геометрии, которые используются при их доказательствах — это теорема синусов и теорема косинусов.
1. 


2. 

Напишите эту формулу для a 2 , b 2 .
Какие же формулы для вычисления площади треугольника вы знаете?
Площадь прямоугольного треугольника. S=
Площадь любого треугольника. S= 




Слайд 4. Площадь треугольника по двум сторонам и углу между ними.
S=½·ab·sinα. Запишите формулу (приложение 1).
Площадь треугольника через радиус вписанной окружности. S = 
Здесь уместно вспомнить, как строится вписанная окружность. Запишите формулу (приложение 1).
Площадь треугольника через R-радиус описанной окружности.

Здесь также можно вспомнить, как строится описанная окружность.
I Формула Герона.
S =
Доказательство первой формулы Герона. Запишите формулу (приложение 1).
Формула площади треугольника по трём сторонам была открыта Архимедом в III в до н.э. Однако соответствующая работа до наших дней не дошла. Эта формула содержится в «Метрике» Герона Александрийского (I в н. э.) и названа в его честь. Герон интересовался треугольниками с целочисленными сторонами, площади которых также являются целыми. Такие треугольники носят название героновых треугольников. Простейшим Героновым треугольником является египетский треугольник
Как посчитать площадь треугольника. если хотя бы одна сторона выражена квадратным корнем? II Формула Герона. Применяя предыдущую формулу, получим следующую.
S= 
Её называют II формулой Герона. И если стороны треугольника а,b,с , то записать ее можно в виде:
S=
Запишите формулу (приложение 1) (см. учебник Атанасяна Л. С. «Геометрия 10-11», 2010 год, стр. 200).
Рассмотрим решение задачи на применение этой формулы.
А вот при решении следующей задачи нам необходимо вспомнить формулы нахождения медиан треугольника. Запишите формулы (приложение 1).
Формулы медиан треугольника (см. учебник Атанасяна Л. С. «Геометрия 10-11», 2010 год, стр. 195).
ma= 
mb=
mc= 
Давайте решим одну замечательную задачу на применение данных формул. (Условие задачи с рисунком на листочках выдаётся каждому ученику. Здесь же они пишут решение. Каждый пункт решения проверяется с использованием слайда). Приложение 2.
А как посчитать площадь треугольника в системе координат? Рассмотрим это на примере. Можно вычислить стороны треугольника, а затем его площадь по II формулой Герона. Но здесь громоздкие вычисления и без калькулятора не обойтись. А нет ли ещё какой-нибудь формулы для вычисления площади треугольника?
Такая формула существует. S= 
Доказательство этой формулы очень громоздкое и мы не будем на нём подробно останавливаться. Если оно вас заинтересует, то можно разобрать его после урока.
Давайте попробуем применить эту формулу при решении задачи, текст которой у вас на тех же листочках. (Приложение 2).
Задача: А(0;0), В(5:7), С(4:-2). Найти площадь треугольника. Отв.19.
Итак, теперь мы знаем 8 формул для нахождения площади треугольника.
Но оказывается это не все формулы.
Существуют ещё формулы и следствия из предыдущих формул.
Вычисление площади треугольника по стороне и прилежащим к ней углам.

Вычисление площади треугольника по стороне и прилежащим к ней углам. Эту формулу можно получить из предыдущей, используя тригонометрическую формулу синуса суммы.
Вычисление площади треугольника через все углы и радиус описанной окружности.

Вычисление площади треугольника через все углы и одну из сторон треугольника.

Вычисление площади треугольника через радиусы вневписанных окружностей. Эту формулу не используют в школе. Но в материалах группы С ЕГЭ встречаются задачи, где можно быстро найти ответ, применив эту формулу.
Итак, мы теперь знаем 13 формул. Но это ещё не предел. С таким же успехом можно получить ещё новые формулы, например, через тригонометрические формулы половинного угла, двойного угла. Такие исследования могут стать стартовой площадкой для написания научно-исследовательской работы.
Слайд 24.
Интернет-ресурсы. На этом слайде вы видите сайт, где есть программа вычисления площадей треугольников по первым семи формулам для самых ленивых. Недостаток этой программы в том, что считает она приближённо в десятичных дробях.
III. Домашнее задание. Приложение 2.
1. А(2;3), В(5:-4), С(-1;-3). Найти площадь треугольника АВС.
2. В ∆АВС a=6, b = 

4) R (радиус описанной окружности).
IV. Итог урока.
Объявить оценки за работу на уроке.
Какие формулы вы сегодня повторили?
Какие формулы вы узнали только сегодня?
Те листочки, на которых вы записали формулы, пусть послужат вам справочным материалом при решении задач на уроке, дома и при подготовке к ЕГЭ.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Видео:Геометрия Площадь треугольника равна 84 см2 а его периметр 72 см Найдите радиус окружности вписаннойСкачать

Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
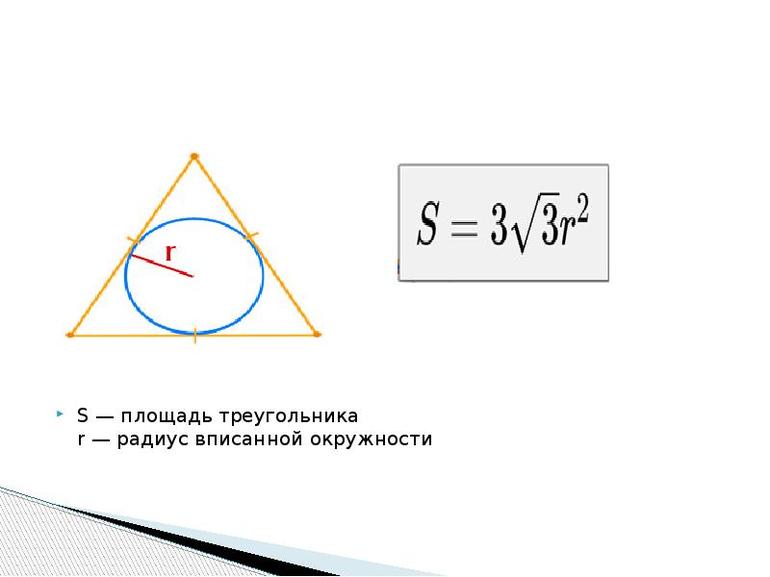
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
💥 Видео
Геометрия Доказательство Площадь треугольника равна произведению его полупериметра и радиусаСкачать

Радиус описанной окружностиСкачать

Площадь треугольника через периметр и радиусСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

Площадь треугольника через радиус вписанной окружностиСкачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать