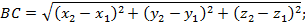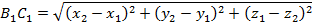Зеркальная симметрия треугольника построение

Вы будете перенаправлены на Автор24

В данной статье мы будем рассматривать понятие зеркальной симметрии в трехмерном пространстве. Но вначале нам надо рассмотреть такие понятия как отображение и движение в пространстве.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Понятие движения

Перед тем, как ввести понятие движения в пространстве, надо ввести определение отображения пространства на себя.

Отображением пространства на себя будем называть такое соответствие любой точке данного пространства какой-либо точке этого же пространства, в котором участвуют все точки из этого пространства.

Введем теперь, непосредственно, определение движения.

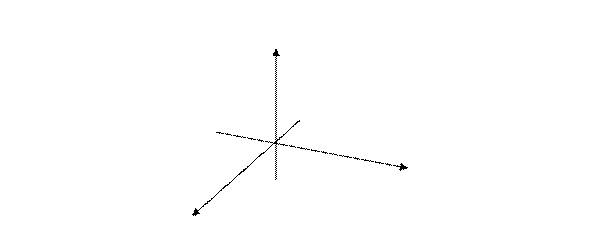
Движением пространства будем называть отображением пространства на себя, которое сохраняется расстояния между соответствующими точками.

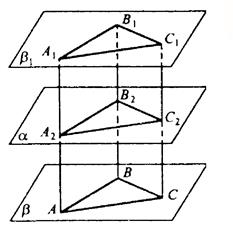
Пример – рисунок 1.

Введем теперь несколько теорем, связанных с понятием движения без доказательства.

При движении отрезок будет отображаться на ему же равный отрезок.

При движении треугольник будет отображаться на равный ему же треугольник.

При движении пирамида будет отображаться на равную ей пирамиду.

Видео:Осевая симметрия. 6 класс.Скачать

Зеркальная симметрия

Перед тем, как определить понятие зеркальной симметрии, введем понятие симметричности точки относительно какой-либо плоскости.

Готовые работы на аналогичную тему

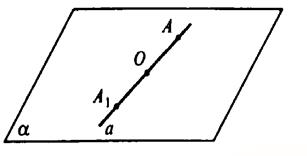
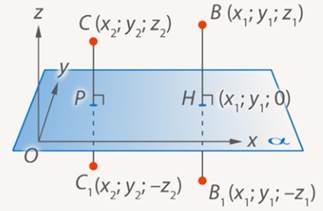
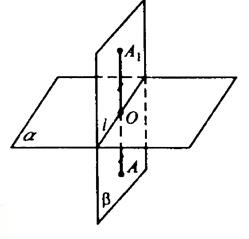
Точки $P$ и $P’$ будем называть симметричными относительно какой-либо плоскости $a$, если прямая $(PP’)$ будет перпендикулярна плоскости $a$ и, при этом, плоскость $a$ будет делить отрезок $[PP’]$ пополам (рис. 2).

Зеркальной симметрией фигуры относительно плоскости будем называть отображение, при котором получается фигура, составленная из точек, симметричных относительно этой плоскости каждой точке начальной фигуры.

Введем следующую теорему:

Зеркальная симметрия – движение.

Пусть нам даны две точки $Z$ и $Z’$ – симметричные относительно плоскости $l$. Построит систему координат $O_$, где плоскость $Oxy$ – это плоскость $l$. Пусть точка $Z$ в этой системе координат имеет координаты $(α,β,γ)$, а точка $Z’$ имеет координаты $(α’,β’,γ’)$. Так как эти точки симметричны относительно плоскости $Oxy$, то эта плоскость будет делить отрезок $[ZZ’]$ пополам, то есть

Так как плоскость $Oxy$ совпадает с нашей плоскостью симметрии, то $α=α’$, $β=β’$.

Возьмем две произвольные точки $X$ и $Y$ с координатами $(α_1,β_1,γ_1)$ и $(α_2,β_2,γ_2)$, соответственно. Расстояние между ними равно

По формулам выше, получим, что симметричные им точки $X’$ и $Y’$ имеют координаты $(α_1,β_1,-γ_1)$ и $(α_2,β_2,-γ_2)$, соответственно. Расстояние между ними равно

То есть зеркальная симметрия сохраняет расстояния, что и доказывает нашу теорему.

С понятием зеркальной симметрии также связано понятие симметричной фигуры:

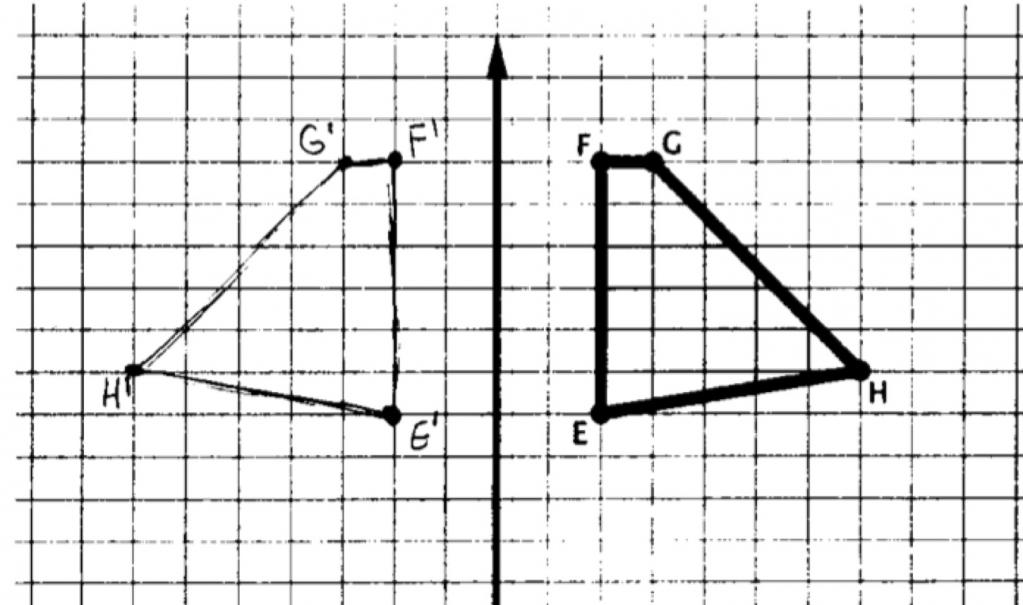
Фигуру будем называть симметричной относительно какого-либо своего сечения, если при такой зеркальной симметрии фигура перейдет в себя (рис. 3).

Видео:11 класс, 11 урок, Зеркальная симметрияСкачать

Пример задачи

Постройте зеркальную симметрию тетраэдра, относительно плоскости $l$, изображенных на рисунке 4.

Для построения такой зеркальной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет перпендикулярна к плоскости $l$ (рис. 5).

Далее, для построения будем использовать определение 3. Точка $A$ перейдет в такую точку $A’$, которая будет принадлежать прямой $a$. Точка $B$ перейдет в такую точку $B’$, которая будет принадлежать прямой $b$. Точка $C$ перейдет в такую точку $C’$, которая будет принадлежать прямой $c$. Аналогично, и точка $D$ перейдет в такую точку $D’$, которая будет принадлежать прямой $d$. Причем, при этом первоначальная плоскость $l$ делит отрезки $[AA’]$, $[BB’]$, $[CC’]$, $[DD’]$ пополам.

Таким образом, зеркальная симметрия этого тетраэдра изображена на рисунке 6.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 17 07 2021

Видео:Геометрия 8 класс (Урок№7 - Осевая и центральная симметрия.)Скачать

Тема: Центральная и зеркальная симметрия

Выполнила ученица 11 А класса Ковалева Дарья

Учитель Багирян Нонна Александровна

· определение и основные свойства

· фигуры, обладающие центральной симметрией

· применение в жизни

· определение и построение

· фигуры, обладающие зеркальной симметрией

· зеркальная симметрия в реальной жизни

Центральной симметрией называют преобразование пространства относительно точки A , переводящее точку X в такую точку X′, что A — середина отрезка XX′. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре.Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.

Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.

· Центральная симметрия является движением;

· Любая прямая при центральной симметрии преобразуется в прямую. Причем, прямая, проходящая через центр, преобразуется в себя. Прямая, не проходящая через центр, преобразуется в параллельную ей прямую. (доказано в задаче 2)

· Центральная симметрия сохраняет расстояния между точками.

· Центральная симметрия переводит отрезки в отрезки, лучи в лучи.

Докажем, что центральная симметрия является движением.

Обозначим буквой O центр симметрии и введем в прямоугольную систему координат Oxyz с началом в точке О. Установим связь между координатами двух точек M (x; y; z) и M₁ (x₁; y₁; z₁), симметричных относительно точки О.

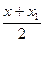
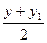
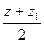
Если точка М не совпадает с центром О, то О – середина отрезка ММ₁. По формулам координат середины отрезка получаем = 0, = 0, =0, откуда x₁ = -x, y₁= -y, z₁ = -z.

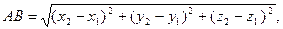
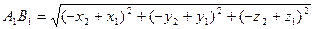
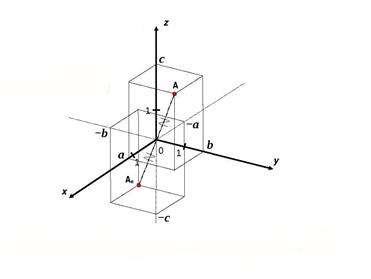
Рассмотрим теперь две точки А (x₁; y₁; z₁) и В (x₂; y₂; z₂) и докажем, что расстояние между симметричными им точкам А₁ и В₁ равно АВ. Точки А₁ и В₁ имеют координаты А₁ (-x₁; -y₁; -z₁ ) и В₁ (-x₂; -y₂; -z₂). По формуле расстояния между двумя точками находим: . Из этих соотношений ясно, что АВ=А₁В₁, что и требовалось доказать.

Построим точку А₀ симметричную точке А относительно точки О.

Пусть А (a; b; c). Тогда координаты A₀ (-a; -b; -c).

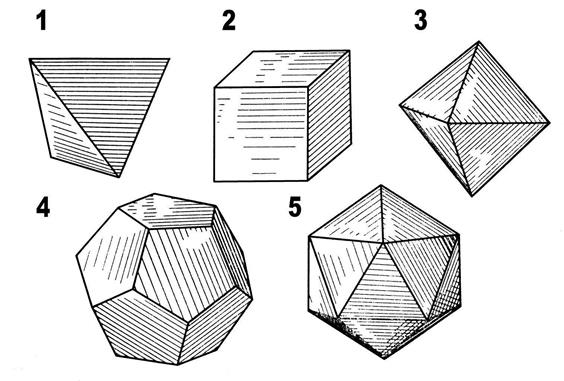
Фигуры, обладающие центральной симметрией.

1. – тетраэдр 2. – куб 3. – октаэдр 4. – додекаэдр 5. – икосаэдр

Применение центральной симметрии в жизни.

В архитектуре центральная симметрия используется реже осевой. Она присуща античным круглым храмам, используется в колоннах.

Колизей Пирамиды в Египте

Башни церквей, замков, колонны проектировались с учетом центральной симметрии. Такие сооружения предавали зданиям массивности. Башни одинаково роскошно выглядели с любой плоскости города.

Центральная симметрия в природе. Она присутствует в снежинках, листьях деревьев и трав, насекомых, цветах, животных.

Центральная симметрия прослеживается в

костюмах казанских татар

№ 1. Найдите координаты точек, в которые переходят точки А (0; 1; 2), В (3; -1; 4), С (1; 0; -2) при центральной симметрии относительно начала координат.

При центральной симметрии относительно начала координат знаки координат искомых точек меняются на противоположные.

А (0; 1; 2) → А₁ (0; -1; -2)

В (3; -1; 4) → В₁ (-3; 1; -4)

С (1; 0; -2) → С₁ (-1; 0; 2)

№ 2. Докажите, что при центральной симметрии: а) прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую; б) прямая, проходящая через центр симметрии, отображается на себя.

а)

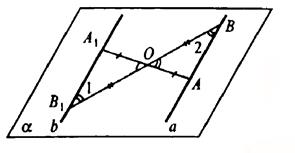
Через центр симметрии и данную прямую можно провести единственную плоскость. Пусть О — центр симметрии, а — данная прямая, α — плоскость, проведенная через О и а. Пусть А ∈ а, построим отрезок ОА.

Продолжим ОА за точку О на расстояние ОА₁=АО. Получим точку А₁, симметричную А.

Пусть В ∈ а, построим отрезок ОВ. Продолжим ОВ за точку О на расстояние ОВ₁=ОВ. Получим точку B₁, симметричную точке В.

Через А₁ и В₁ проведем прямую b. Рассмотрим ΔAОВ и ΔА₁ОВ₁⋅AО=А₁О, ВО=ОВ₁, ΔАОВ=ΔА₁ОВ₁ как вертикальные, следовательно, ΔAОВ=ΔА₁ОВ₁.

Тогда, ∠1=∠2 и а || b.

Пусть А ∈ а. Симметричная ей точка А₁ тоже принадлежит прямой а; АО=ОА₁.

Точка А произвольна, следовательно, любая точка прямой, а также симметричная точка относительно центра О лежат на прямой а, следовательно, прямая а переходит сама в себя при условии, что проходит через центр симметрии.

Зеркальной симметрией (симметрией относительно плоскости α) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М₁ относительно плоскости α.

Докажем, что зеркальная симметрия является движением.

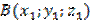
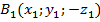
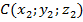
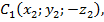
Для этого введем прямоугольную систему координат Оxyz так, чтобы плоскость Oxy совпала с плоскостью симметрии, и установим связь между координатами точек и , и симметричных относительно плоскости Oxy

Найдем длину отрезков BC и B₁C₁ по формуле расстояния между точками:

Отсюда BC = B₁C₁, значит, зеркальная симметрия является движением.

Отсюда следует, что зеркальная симметрия обладает следующими свойствами:

· переводит прямые в прямые

· полупрямые – в полупрямые

· отрезки – в отрезки

· плоскости – в плоскости

· сохраняет углы между прямыми.

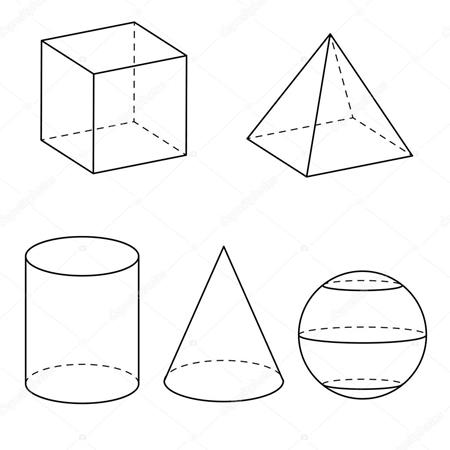
Фигуры, обладающие зеркальной симметрией

(слева на право) – куб, пирамида, цилиндр, конус, сфера

Зеркальная симметрия в жизни

Наиболее распространена вархитектуре зеркальная симметрия.

Эйфелева башня Тадж Махал

Зеркальная симметрия в природе может быть представлена отражением изображения в воде.

Животные, растения, и человек тоже могут послужить примерами зеркальной симметрии. Однако назвать их идеальными примерами сложно, ведь даже лицо человека, которое на первый взгляд может показаться симметричным, таковым не является.

№ 1. Найдите координаты точек, в которые переходят точки А (0; 1; 2), В (3; -1; 4), С (1; 0; -2) при зеркальной симметрии относительно координатных плоскостей.

Если плоскость симметрии — плоскость Оxy, то меняем значение координаты z на противоположную (т.к. ось Оz перпендикулярна плоскости Оxy, О – точка их пересечения)

А (0; 1; 2) → А₁ (0; 1; -2)

В (3; -1; 4) → B₁ (3; -1; -4)

С (1; 0; -2) → C₁ (1; 0; 2)

Аналогично решение с другими плоскостями.

Если плоскость симметрии — плоскость Оyz, то меняем значение координаты x.

А (0; 1; 2) → А₁ (0; 1; 2)

В (3; -1; 4) → B₁ (-3; -1; 4)

С (1; 0; -2) → C₁ (-1; 0; -2)

Если плоскость симметрии — плоскость Оxz, то меняем значение координаты y.

А (0; 1; 2) → А₁ (0; -1; 2)

В (3; -1; 4) → B₁ (3; 1; 4)

С (1; 0; -2) → C₁ (1; 0; -2)

№ 2. При зеркальной симметрии относительно плоскости α плоскость β отображается на плоскость β₁. Докажите, что если: а) β || α, то β₁ || α; б) β ┴ α, то β₁ совпадает с β.

а) Выберем три точки в плоскости А, В, С, не лежащие на одной прямой. Проведем АА₂⊥α, ВВ₂ ⊥α, СС₂ ⊥α. Продолжим эти отрезки за точки А₁, B₁, C₁ так, что А₂А₁=АА₂, B₂B₁=BB₂, C₂C₁=CC₂.

Плоскость β₁ проходит через точки А₁, В₁ и C₁, она — единственная.

Если две пересекающиеся прямые (ВА и ВС) одной плоскости (β) параллельны двум прямым (B₁A₁ и В₁С₁) другой плоскости (β₁), то эти плоскости параллельны: β₁ || β.

б)

Пусть α⊥β. Возьмем произвольную точку А ∈ β и построим АО перпендикулярно плоскости α. Продолжим отрезок за точку О на расстояние ОА₁=АО.

Две плоскости взаимно перпендикулярны и к одной из них проведен перпендикуляр, имеющий общую точку с другой плоскостью, тогда этот перпендикуляр весь лежит в этой плоскости, т.е.

АО⊂β, следовательно, и АА₁ ⊂β.

Таким образом, каждая точка плоскости β отображается в точку, ей симметричную, которая тоже принадлежит плоскости β. тогда, плоскость β отображается сама на себя, или β₁ совпадает с β.

Видео:ВПР 6 класс. 12 задание. Фигура симметиичная данной относительно оси.Скачать

Зеркальная симметрия: определение и примеры

Какие примеры зеркальной симметрии можно встретить в повседневном мире и всегда ли это красиво? Что это такое? Какие характеристики ее определяют? Отражательную симметрию можно найти в геометрических фигурах, математике, природе и искусственном мире.

Видео:Центральная симметрия. 6 класс.Скачать

Что такое рефлексивная симметрия?

Какое можно дать определение? Зеркальная симметрия возникает, если при разделении объекта или формы пополам, каждая половина будет отражать другую. Иногда объекты или формы имеют более одной линии симметрии. Возьмем, к примеру, букву H. Сколько линий симметрии она имеет? Если вы ответили две, вы правы. Есть два способа сделать линию, чтобы каждая половина отражала другую половину.

Видео:Осевая симметрия, как начертить треугольники симметричноСкачать

Можно ли считать человеческое лицо симметричным?

Что, если вы посмотрите на собственный снимок, особенно фотографию как в паспорте, и нарисуете линию прямо посередине вашего лица, от лба до подбородка? Что бы вы заметили? Разве не казалось бы, что одна сторона вашего лица является отражением другой? Например, с каждой стороны будет глаз. Обе половины ваших губ выглядели бы почти одинаково. Если нет шрамов от какой-либо травмы, обе половины вашего носа выглядели бы одинаково. В идеале ваша гипотетическая фотография паспорта — всего лишь один из примеров зеркальной симметрии, также известной как двусторонняя или линейная симметрия. Линия, которую вы нарисовали, чтобы разделить ваше лицо, называется линией симметрии.

Однако, поскольку люди имеют неконтролируемые различия, наши лица не всегда могут рассматриваться как идеальные примеры. Например, у некоторых из нас может быть одна сторона лица красивее, чем вторая. Если вы внимательно посмотрите в зеркало, вы можете заметить, что один из ваших глаз немного меньше другого, одна скула шире, чем другая, и так далее. Многие аспекты человеческого облика могут искажать понятие истинной рефлексивной симметрии, поэтому истинная зеркальная симметрия должна удовлетворять определенным условиям.

Видео:Осевая и центральная симметрия, 6 классСкачать

Примеры рефлексивной симметрии

Многие буквы алфавита имеют зеркальную симметрию. Некоторые используют вертикальную линию; некоторые используют горизонтальную линию. Какие есть примеры зеркальной симметрии в геометрии? Формы также могут демонстрировать рефлексивную симметрию, такую ​​как круги и квадраты, которые имеют четыре линии симметрии. В зависимости от типа треугольника можно иметь нулевую, одну или три линии.

Поскольку мы все больше и больше изучаем нашу окружающую среду и наше окружение, мы видим, что природа может быть описана математически. Красота цветка, величие дерева, даже скалы могут проявлять зеркальную симметрию в природе. Есть и другие примеры, которые можно найти в кристаллографии или даже на микроскопическом уровне. Кажется, что везде, куда мы сейчас смотрим, наши глаза сначала обращаются к существующим образцам симметрии.

Видео:Построение треугольника, симметричного данному относительно точки, принадлежащей его сторонеСкачать

Существуют разные виды симметрии

• Радиальная симметрия — это вращательная симметрия вокруг неподвижной точки, известной как центр. Радиальная симметрия может быть классифицирована как циклическая или двугранная. Примеры в природе: морская звезда, медузы, цветы, змеи, насекомые, соты пчел. Восточная белая сосна имеет интересную симметрию на стволе. Каждый год по мере роста дерева он развивает новое кольцо ветвей.
• Диэдральные симметрии отличаются от циклических тем, что они имеют симметрию отражения в дополнение к вращательной симметрии.

Видео:6 класс, 26 урок, СимметрияСкачать

В математике

Зеркальная симметрия является симметрией относительно отражения. То есть фигура, которая не изменяется при отражении, имеет рефлекторную симметрию. Если бы форму нужно было сгибать пополам по оси, две половины были бы одинаковыми: две половины — зеркальные изображения друг друга. Таким образом, квадрат имеет четыре оси симметрии, поскольку существует четыре разных способа свернуть его и согласовать края. Круг имеет бесконечно много осей симметрии.

Симметричные геометрические фигуры 2D-формы с отражательной симметрией, равнобедренная трапеция, шестигранники. восьмиугольники — это все примеры зеркальной симметрии в геометрии. Треугольники с симметрией отражения являются равнобедренными. Все односторонние многоугольники имеют две простые отражающие формы: одну с линиями отражений через вершины и одну по краям.

Видео:Ось симметрииСкачать

В природе

Многие животные являются симметричными. Такие организмы имеют отражательную симметрию в сагиттальной плоскости, которая разделяет тело вертикально на левую и правую половинки с одним из каждого органа чувств и пары конечностей с обеих сторон. Большинство животных имеют двустороннюю симметричность, вероятно, потому что это поддерживает движение вперед и баланс.

Видео:ЭТИ Правила Работают на 100.Бесценные Советы Черниговской о том, как сохранить Ясный Ум до старостиСкачать

В архитектуре

Зеркальная симметрия часто используется в архитектуре. Она также встречается в дизайне древних сооружений, таких как Стоунхендж. Симметрия была и является по сей день ключевым элементом в некоторых стилях архитектуры, так как считается символом красоты, гармонии и совершенства. В архитектуре симметрия — это отражение общих форм, форм или углов по центральной линии или точке, называемой осью. В принципе, компоненты, которые отражают друг друга по оси, являются симметричными. Это один из старейших и наиболее постоянно используемых принципов в архитектуре.

Симметрия помогает связать различные элементы структуры вместе в единое целое. Она также широко используется для создания чувства рационального порядка и спокойной логики, предпочтительной эстетики древних греков и римлян. Мы можем смотреть на симметрию во многих масштабах, от отношения между отдельными деталями, до макета полной структуры и даже до всех городских центров, построенных на симметричной сетке.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Основополагающий принцип устройства мира

Симметрия – везде, и поэтому она является эффективным методом познания природы. В природе она обеспечивает устойчивость, равновесие, надежность и прочность. Симметричные формы более устойчивы к различным воздействиям. Существует бесчисленное множество видов симметрии, однако, для живой и неживой природы также является вполне естественной определенная асимметрия.

Для организации всех живых структур свойственно геометрическое подобие. например, кленовые листочки похожи друг на друга, лист березы подобен листу березы и так далее. Что бы ни происходило в процессе жизнедеятельности живой клетки, которая принадлежит целому организму и выполняет функцию его воспроизведения в новый отдельный субъект, она является все лишь отправной точкой. В результате деления эта маленькая ячейка преображается и формируется в объект, схожий по всем показателям первоначальному.

Живым организмам симметрия оказывает неоценимую услугу, в первую очередь, это равновесие при передвижении и функционировании. Это можно наблюдать и в растительном мире. Симметричное расположение ветвей обеспечивает стволам деревьев определенную устойчивость тем, что регулирует распределение силы тяжести. Интересен то факт, что большинство деревьев и имеют конусообразную вершину. С чем это связано? Все в природе хорошо продумано: форма конуса дает возможность не только верхним, но и нижним листьям получать достаточное количество солнечных лучей, не говоря уже об установлении центра тяжести, от которого зависит устойчивость растения.

Симметрия вместе с асимметрией успешно сосуществуют в нашем мире, и та и другая нашли свое отражение в генах живых организмов, они гармонично дополняют друг друга.

💥 Видео

Геометрия 8 Осевая и центральная симметрияСкачать

Неравномерная темперация и биения центра объектовСкачать

Центральная симметрияСкачать

Симметрия относительно точки (центральная симметрия). Пример 2Скачать

Центральная и осевая симметрии. Геометрия 7 класс.Скачать

48. Осевая и центральная симметрииСкачать

Зеркальная симметрияСкачать