Вневписанная окружность в треугольнике ортоцентр

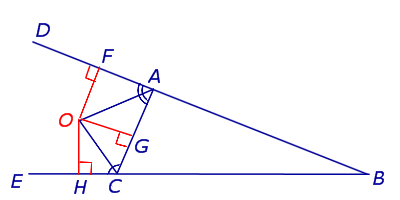
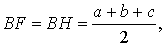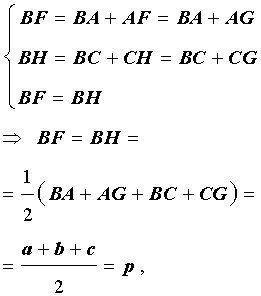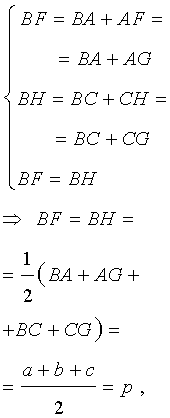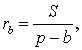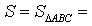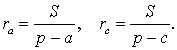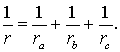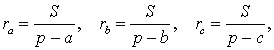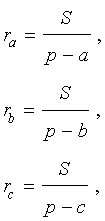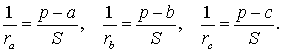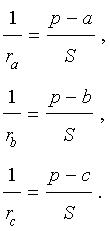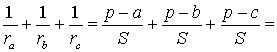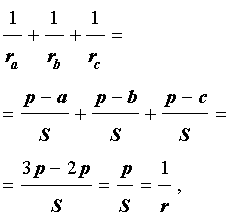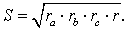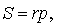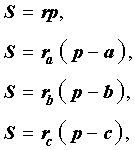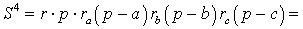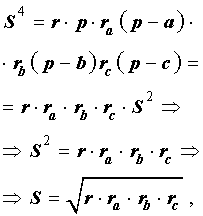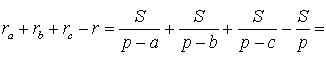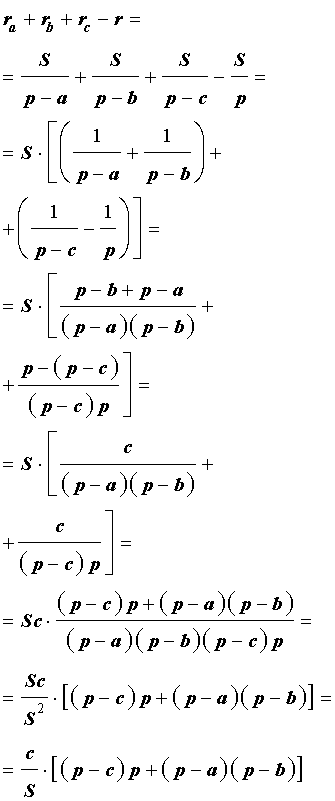Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.

Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).

Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:

Следовательно, справедливо равенство

Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства

откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .

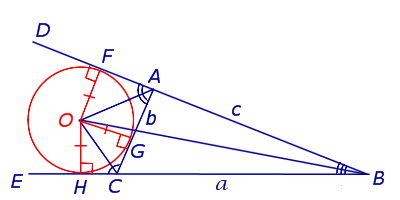
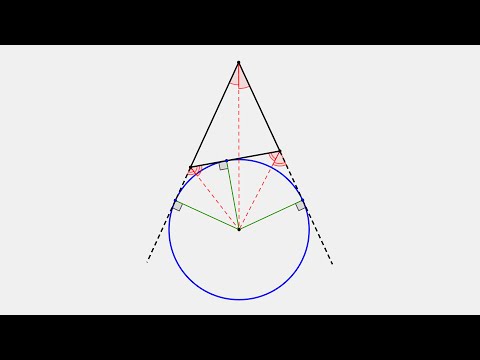
Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).

Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.

Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом r_b .

Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.

Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство

где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:

где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.

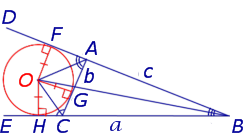
Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле

где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .

Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства

Следовательно, справедливо равенство

что и требовалось доказать.

Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:

Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:

Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности

,

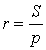
что и требовалось доказать.

Теорема 5 . Площадь треугольника можно вычислить по формуле

Доказательство . Перемножим формулы

что и требовалось доказать.

Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:

Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим

Преобразуем выражение, стоящее в квадратной скобке:

Видео:Вневписанная окружностьСкачать

Вневписанная окружность треугольника.

Определение.

Окружность, касающаяся стороны треугольника и продолжения двух других его сторон, называется вневписанной окружностью треугольника.

Теорема 1.

Центр окружности, вневписанной в треугольник, есть точка пересечения биссектрис двух внешних и одного внутреннего угла треугольника.

Доказательство.

BF — биссектриса ∠JBG, следовательно F равноудалена от сторон данного угла.

СF — биссектриса ∠JСH, следовательно F равноудалена от сторон данного угла.

Следовательно, точка F равноудалена от сторон ∠BAC.

Таким образом, точка F — центр окружности, касающейся стороны BC и продолжения сторон AB и AC. По определению данная окружность называется вневписанной окружностью треугольника.

Теорема 2.

Отрезок, соединяющий вершину треугольника с точкой касания вневписанной окружности и противолежащей стороны, делит треугольник на два треугольника равного периметра.

Доказательство.

BJ=BG, GC=CH и AJ=AH (свойство отрезков касательных, проведенных из одной точки к окружности).

P_ΔABC=AB+ BC +AC=AB+ BG + GC +AC=AB+ BJ + AC +CH=AJ+AH.

Так как AJ=AH, то P_ΔABC/2=AJ=AH и P_ΔABC/2+AG=AJ+AG=AH+AG=AB+BG+GA=AC+CG+GA.

Следовательно, отрезок AG поделил треугольник ABC на два треугольника равного периметра P_ΔABC/2+AG.

Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Вневписанная окружность в треугольнике ортоцентр

Предметом нашего исследования являются ортоцентрические треугольники и их свойства.

Цель – изучение свойств ортоцентрических треугольников и исследование путей их использования для решения задач.

1) выяснить, что такое ортотреугольник;

2) изучить и проанализировать свойства ортотреугольников;

3) рассмотреть возможное применение

этих свойств для решения задач.

4) подвести итоги.

Во время выполнения поставленных задач нами был использован описательный метод исследования, изучение и обобщение.

Практическая значимость: результаты проведенного исследования могут стать опорой для решения олимпиадных задач, задач ЕГЭ и ОГЭ с использованием свойств отроцентрических треугольников.

Глава 1. Исторические сведения и свойства

§ 1. Что такое ортоцентрический треугольник?

Ортотреуго́льник (ортоцентрический треугольник) — это треугольник ΔA_1B1C₁, вершины которого являются основаниями высот треугольника ∆ABC. Для ортотреуго́льника (для ортоцентрического треугольника) ΔA_1B1C₁ сам треугольник ∆ABC является треугольником трёх внешних биссектрис. То есть отрезки AB, BC и CA являются тремя внешними биссектрисами треугольника ΔA_1B1C₁.

§ 2. Исторические сведения

В начале 18 века итальянский инженер и математик Фаньяно дей Тоски поставил перед собой такую задачу: вписать в остроугольный треугольник АВС треугольник наименьшего периметра так, чтобы на каждой из сторон данного треугольника лежала одна вершина вписанного. Аналитическое решение этой задачи было опубликовано в 1755 году. Было доказано, что существует единственный треугольник наименьшего периметра KMN, его вершина K – основание высоты CK. Искомым треугольником всегда будет ортотреугольник KMN.

§ 3.Свойства ортотреугольников

1.Теорема о подобии треугольников. Ортотреугольник отсекает треугольники, подобные данному.

В остроугольном треугольнике проведены высоты , . Найдем углы треугольника , если , а .

Прямоугольные треугольники и имеют общий угол при вершине С, они подобны, поэтому .

Из этого равенства следует, что в треугольниках и стороны, прилежащие к общему углу при вершине С, пропорциональны. Следовательно, по второму признаку подобия треугольников подобен . В подобных треугольниках против соответственных сторон лежат равные углы, поэтому угол , .

Аналогично можно доказать подобие треугольников и ; и , если провести высоту CC₁. При этом , и .

Как следствие данной теоремы, верно следующее утверждение:

Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.

Среди всех треугольников, вписанных в данный треугольник, только ортотреугольник обладает указанным свойством.

І. Ортоцентрический треугольник H₁H₂H₃ В остроугольном треугольнике ABC соединим отрезками основания высот H₁,H₂,H₃ (рис. 1). Получим

треугольник H₁H₂H₃. Рассмотрим некоторые свойства этого треугольника, которые используют при решении задач.

Свойство 1. Стороны ортоцентрического треугольника H₁H₂H₃ антипараллельны сторонам треугольника ABC.

Доказательство. Обозначим точку H — точку пересечения высот треугольника ABC (ортоцентр). Опишем окружность около четырёхугольника AH₂HH₃. Тогда ∠AH₂H₃ = ∠AHH₃ = ∠ABC, значит, сторона H₂H₃ антипараллельна стороне BC. Аналогично доказывается антипараллельность двух других сторон треугольника

Свойство 2. Высоты треугольника ABC являются биссектрисами внутренних углов треугольника H₁H₂H₃.

Свойство 3. Отрезок OA перпендикулярен отрезку H₂H₃.

Доказательство. Действительно, если описать окружность около треугольника H₁H₂H₃, дуги, на которые опираются углы ∠H₂H₁A и ∠AH₁H₃, равны, а значит, OA⊥H₂H₃ (рис. 2).

Свойство 4. Вершины треугольника ABC являются центрами вневписанных окружностей ортоцентрического треугольника H₁H₂H₃ (рис. 3).

Доказательство. Поскольку отрезок AH₂ перпендикулярен биссектрисе H₂B, а AH₃⊥CH_3, то пересечение отрезков AH₂ и AH₃, — точка A есть центр вневписанной окружности, касающейся стороны H₂H₃.

Свойство 5. Имеет место формула p_H = h_asinA, где p_H — полупериметр треугольника H₁H₂H₃, h_a — высота AH₁.

Доказательство. Из точки A опустим перпендикуляр AF на прямую H₁H₃ (рис.3). Поскольку∠H₁AF = ∠H₃H₁B (углы с взаимно перпендикулярными сторонами), то ∠HAF = ∠A и H₁F = h_asinA (из треугольника H A1 F), или p_H = h_asinA.

Свойство 6. Имеет место формула S = Rp_H, где S — площадь треугольника ABC, R — радиус окружности, описанной около треугольника ABC.

Доказательство. Действительно, поскольку p_H = h_asinA, то

p_H= sinA, и S = Rp_H(a — длина стороны BC).

Свойство 7. Окружность Леонарда Эйлера.

Доказательство. Опишем окружность около треугольника H₁H₂H₃. Докажем, что окружности (обозначим её γ_e), кроме точек H₁, H₂, H₃, принадлежат середины отрезков AH, BH, CH (их называют точками Эйлера и обозначают E₁, E₂, E₃), ещё три точки M₁, M₂, M₃ — середины сторон BC, AC, AB. Начнём с точек Эйлера. Заметим, что доказательство нестандартно (рис. 4).

Поскольку прямая H H1 (рис. 4) принадлежит биссектрисе угла ∠H₂H₁H₃, то точка её пересечения с окружностью γ_e, описанной

около треугольника H₁H₂H₃, будет серединой дуги H₂H₃, то есть точкой W₁ треугольника H₁H₂H₃, а точка A — центром вневписанной

окружности (свойство 4).

По теореме Мансиона ( IW₁ = W₁I_a = W₁B = W₁C): AE₁ = E₁H. Значит, точка совпадает с серединой отрезка IW₁ для треугольника H₁H₂H₃ с точкой E₁. Поскольку точки B и C также центры вневписанных окружностей, то утверждение относительно середин отрезков AH, BH и CH доказано. Докажем, что середины AC, BC и AB (точки M₁, M₂, M₃) принадлежат окружности γ_e.

Воспользуемся свойством вневписанных окружностей с центрами Ib и I_c. Пусть W₁ A — точка, диаметрально противоположная точке W₁. Тогда W₁ A — середина отрезка IbI_c. Пусть окружность γ_e пересекает сторону BC в точке X (рис. 4). Поскольку ∠E₁H₁X₁ = 90°, то точки X и E₁ диаметрально противоположны, а поскольку точка E₁ есть точкой W₁ окружности, то точка X совпадает с серединой отрезка BC (точки B и C — центры вневписанных окружностей). Теорема об окружности Эйлера для треугольника ABC доказана новым способом.

ІІ. Ортоудвоенный треугольник

Высоты AH₁, BH₂, CH₃ продолжим до пересечения с описанной окружностью (рис. 5).

Получим треугольник N_1N2N3, который назовём ортоудвоенным. Поскольку HH₁ = H_1N1, HH₂ = H_2N2, HH₃ = H_3N3, то этот треугольник гомотетичен треугольнику H₁H₂H₃ с центром гомотетии — серединой отрезка OE ( E — центр окружности Эйлера) и коэффициентом гомотетии k =

Свойство 1. Вершины треугольника ABC делят дуги N_2N3, N_3N1, N_1N2 пополам.

Доказательство. Действительно, ∠ N_2N1A = ∠ N_3N1A.

Свойство 2. Высоты треугольника ABC принадлежат биссектрисам внутренних углов треугольника N_1N2N3.

Доказательство. Действительно, это следует из свойства 1.

Свойство 3. Радиус OA перпендикулярен отрезкам N_2N3 и H₂H₃.

Доказательство. Действительно, это следует из свойства 1.

Свойство 4. Точка, симметричная ортоцентру H относительно середины M₁ отрезка BC принадлежит окружности, описанной около треугольника

Доказательство. Проведём диаметр AA₁ (рис.6) и найдём точку X, гомотетичную точке A₁. Поскольку A₁X = XH, то отрезок OX — средняя линия треугольника

AA₁H. Значит, он параллелен AH и равен

AH, то есть OX = OM₁ и точка X совпадает с точкой M₁ — серединой отрезка BC.

Свойство 5. Прямая Эйлера. Центроид M треугольника ABC принадлежит отрезку OH.

Доказательство. Проведём отрезок AM₁ (рис. 6). Он пересечёт OH в точке Y. Поскольку то M₁M : AM = 1 : 2, а значит, точка Y совпадает с точкой M₁.

Окружность девяти точек

Около треугольника H₁H₂H₃ опишем окружность γ_e. Её центр делит пополам отрезок OH (точка E). Середины отрезков AH, BH, CH (точки E₁, E₂, E₃) гомотетичны точкам A, B и C и принадлежат окружности γ_e.

Докажем, что точки M₁, M₂, M₃ принадлежат окружности γ_e.

Доказательство. Действительно, точки A₁ и H симметричны относительно точки B. Кроме того, точки A₁ и M₁ гомотетичны, а значит, точка M₁ принадлежит окружности γ_e.

ІІІ. Ортоцентрический треугольник Q₁Q₂Q₃

Опишем окружность около треугольника ABC и построим точки W₁,W₂, W₃ (середины дуг BC, AC, AB) (рис. 7).

Точку пересечения хорд W₂W₃ и AW₁ обозначим Q₁. Аналогично получим точки Q₁ и Q₃. По теореме «листа трилистника» имеем: IW₁ = W₁C. Поскольку ∪ AW₂ = ∪ W₂C, то

а значит, треугольник Q₁Q₂Q₃ — ортоцентрический треугольник треугольника W₁W₂W₃. В равнобедренном треугольнике IW₁C IQ₃ = Q₃C. Аналогично, IQ₁ = Q₁A, следовательно, стороны треугольника Q₁Q₂Q₃ вдвое меньше соответственных сторон треугольника ABC. Поэтому (применяем формулу S = Rp_H ) площадь треугольника W₁W₂W₃ . (1°)

Поскольку окружность, описанная около треугольника Q₁Q₂Q₃, есть окружность Эйлера треугольника W₁W₂W₃, то девять точек принадлежат одной окружности: середины отрезков W₁W₃, W₂W₃, W₁W₂, IW₁, IW₂, IW₃, IA, IB, IC.

ІV. Ортоцентрический треугольник ABC Рассмотрим треугольник, вершины которого — центры вневписанных окружностей I_a, Ib, I_c (рис.8).

Ортоцентрическим треугольником этого

треугольника будет треугольник ABC, так как

каждая из его вершин есть пересечение внутренней и внешней биссектрис. Поскольку радиус окружности, описанной около треугольника ABC будет R, то радиус окружности, описанной около треугольника I_aIbI_c будет 2R, а площадь S_IaIbIc=2R⋅p.

Поскольку окружность, описанная около треугольника ABC, является окружностью Эйлера треугольника I_aIbI_c, то девять точек принадлежат одной окружности: вершины треугольника ABC, точки W₁, W₂, W₃, середины

V. Треугольник, подобный ортоцентрическому треугольнику H₁H₂H₃

Через вершины A, B и C проведём касательные к окружности, описанной около треугольника ABC. Получим треугольник T₁T₂T₃ (рис. 9).

тангенциальным) вычисляют по формуле:

S_T=R⋅p_T, где R — радиус окружности, вписанной в треугольник T₁T₂T₃.

Глава 2. Применение.

§ 1 Применение свойств ортотреугольника для решения задач

Задача 1.

Пусть и – высоты треугольника АВС. Докажите, что треугольник подобен треугольнику АВС. Чему равен коэффициент подобия?

подобен треугольнику АВС по теореме 1. Коэффициент подобия . В прямоугольных треугольниках и , . Значит, .

Следствием данной задачи будет следующее утверждение: каждая сторона ортотреугольника равна произведению противолежащей стороны на косинус противолежащего угла исходного треугольника.

Задача 2.

Треугольник АВС остроугольный, и угол ВАС равен α. На стороне ВС как на диаметре построена полуокружность, пересекающая стороны АВ и АС в точках Р и Q соответственно. Найдите отношение площадей треугольников АВС и APQ.

Поскольку и — высоты треугольника , треугольник подобен с коэффициентом подобия , поэтому

Задача 3

В остроугольном треугольнике АВС проведены высоты АD, ВЕ и СF. Докажите, что pR=Pr, где p-периметр треугольника EDF, Р – периметр треугольника АВС.

Решение(без применения свойств):

1. Т.к. и согласно задаче 1 , то . ,

Пусть О – центр описанной окружности , R – ее радиус. Тогда Т.к. по т. синусов , то после подстановки, получаем .

Аналогично и , т.е. . Поскольку и , то , что и требовалось доказать.

Решение(без применения свойств):

По свойству 6 . , тогда , что и требовалось доказать.

Задача 4

Треугольник АВС остроугольный, и . Определите углы высотного треугольника.

1. Строим высоты , , .

Задача 5.

Т.к. — равнобедренный, то — высота, медиана, биссектриса ;.

4. Т.к. подобен , то; .

5. ||, а это значит, что подобен .

7. По т. Пифагора .

Задача 6

В равнобедренном треугольнике ABC(AB = BC)проведены высоты AA₁,

Т.к. подобен , то и (1)

по гипотенузе и острому углу, т.к рассматриваемые треугольники прямоугольные, .

Т.к. и , отсекая пропорциональные отрезки, то ||.

Известно, что , , поэтому, подставив данные в (1), получим ,

Глава 3. Анкетирование учащихся

Всем ученикам 10 и 11 классов я задала по 4 вопроса:

Знаете ли вы об ортоцентрических треугольниках?

Применяли ли вы свойства ортоцентрических треугольников при решении задач?

Как вы считаете, можно ли облегчить решение задач, используя эти свойства?

Хотели бы вы научиться решать задачи на применение свойств ортоцентрических треугольников?

Подсчитав ответы «да», я получила следующие результаты:

💥 Видео

ЕГЭ-2020. №16. Вневписанная окружность🚀 Ортоцентр. Теорема Карно, Бланшета, Чевы, Менелая🔥Скачать

✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать

Это будет на ЕГЭ 2020 по математике. Вписанная и вневписанная окружности.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

ВСЕ свойства ортоцентра для №16 на ЕГЭ 2023 по математикеСкачать

№16 ЕГЭ 2023 по математике. Свойство ортоцентра за 5 минут. Четко и без водыСкачать

✓ Красивый факт про ортоцентр | Осторожно, спойлер! | Борис ТрушинСкачать

Вневписанная окружностьСкачать

№16 из ЕГЭ2022 и олимпиады. Красивое доказательство свойства ортоцентра остроугольного треугольникаСкачать

Вневписанная окружность | Теоремы об окружностях - 3Скачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

М2112. Ортоцентр и середины сторон треугольника, параллелограммСкачать

Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Вневписанная окружность. Теория | Профильная математика в онлайн - школе СОТКАСкачать

Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать

Вебинар 3. Лемма о трезубце. Теорема Менелая, Чевы, Ван - Обеля. Свойства ортоцентра.Скачать