Замечательное свойство окружности.

ОКРУЖНОСТЬ

i. 1. Окружность.Окружностью называется геометрическое место точек плоскости, удаленных от данной точки, называемой центром окружности, на одно и то же положительное расстояние.

ii. Свойства окружности.

1) Диаметр, перпендикулярный хорде, делит ее пополам.

2) Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.

3) Серединный перпендикуляр к хорде проходит через центр окружности.

5) Равные хорды удалены от центра окружности на равные расстояния.

6) Хорды окружности, удаленные от центра на равные расстояния, равны.

7) Окружность симметрична относительно любого своего диаметра.

8) Дуги окружности, заключенные между параллельными хордами, равны.

9) Из двух хорд больше та, которая менее удалена от центра.

10) Диаметр есть наибольшая хорда окружности.

Замечательное свойство окружности.

1) Геометрическое место точек M, из которых отрезок AB виден под прямым углом (ÐAMB =90 0 ), есть окружность с диаметром AB без точек A и B.

2) Геометрическое место точек M, из которых отрезок AB виден под острым углом (ÐAMB 0 ) есть внешность круга с диаметром АВ без точек прямой AB.

3) Геометрическое место точек M, из которых отрезок AB виден под тупым углом (ÐAMB > 90 0 ), есть внутренность круга с диаметром АВ без точек отрезка AB.

3.Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде.

4.Центр окружности, описанной около прямоугольного треугольника — середина гипотенузы.

5. Касательная к окружности.Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности.

1) Касательная перпендикулярна радиусу, проведенному в точку касания.

2) Если прямая l, проходящая через точку на окружности, перпендикулярна радиусу, проведенному в эту точку, то прямая l — касательная к окружности.

3) Если прямые, проходящие через точку M, касаются окружности в точках A и B, то MA=MB (Касательные, проведенные к окружности из одной точки, равны).

4) Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

5) Теорема о биссектрисах треугольника.Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.

6.Радиус окружности, вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c, равен .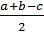

7.Если M — точка касания со стороной AC окружности, вписанной в треугольник ABC, то AM=p−BC, где p — полупериметр треугольника.

8.Окружность касается стороны BC треугольника ABC и продолжений сторон AB и AC. Тогда расстояние от вершины A до точки касания окружности с прямой AB равно полупериметру треугольника ABC.

9.Окружность, вписанная в треугольник ABC, касается сторон AB, BC и AC соответственно в точках K, L и M. Если ÐBAC = α, то ÐKLM = 90 0 − .

10.Даны окружности радиусов r и R (R > r). Расстояние между их центрами равно a (a>R + r). Тогда отрезки общих внешних и общих внутренних касательных, заключенные между точками касания, равны соответственно a 2 −(R−r) 2 и a 2 −(R+r) 2 .

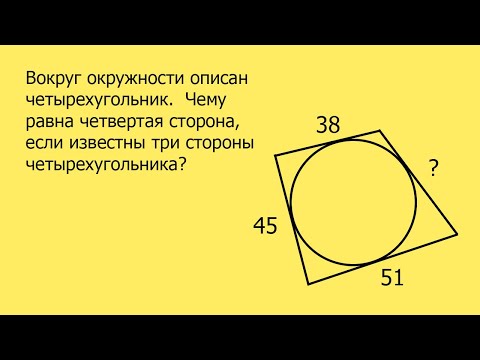
11.Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.

12. Касающиеся окружности.Говорят, что две окружности касаются, если они имеют единственную общую точку (точка касания).

1) Точка касания двух окружностей лежит на их линии центров.

2) Окружности радиусов rиRс центрами O₁ и O₂ касаются внешним образом тогда и только тогда, когда R + r = O₁O₂.

Содержание

math4school.ru
Свойства и признаки окружности
«Уникальные» свойства окружности
«Не уникальные» свойства окружности
Доказательство признака 2
Доказательство признака 6
Окружность
Основные термины
Касательная
Свойства касательной
Хорда
Свойства хорд
Свойства окружности
Теорема о касательной и секущей
Теорема о секущих
Углы в окружности
Свойства углов, связанных с окружностью
Длины и площади
Вписанные и описанные окружности
Окружность и треугольник
Окружность и четырехугольники
📹 Видео

Видео:Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать

math4school.ru

Видео:Уроки геометрии. Одно замечательное свойство четырехугольника, описанного вокруг окружности.Скачать

Свойства и признаки окружности

Хорошо известно определение окружности как геометрического места точек, равноудаленных от некоторой фиксированной точки .

Однако определить окружность можно и многими другими способами. Приведем несколько примеров.

1. Окружность есть геометрическое место точек, сумма квадратов расстояний от которых до двух заданных точек постоянна и больше половины квадрата расстояния между этими точками.

2. Окружность есть геометрическое место точек, отношение расстояний от которых до двух данных точек А и В постоянно и не равно 1.

Такая окружность называется окружностью Аполлония точек А и В .

3. Окружность диаметра AB – это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом.

Окружность обладает многими красивыми свойствами, доказательство которых не представляет труда. Сложнее определить, являются ли эти свойства также и признаками окружности, т.е. существуют ли другие кривые, обладающие ими. Перечислим сначала некоторые из свойств окружности, не присущие никаким другим кривым.

«Уникальные» свойства окружности

1. Два угла с вершинами на окружности, опирающиеся на одну и ту же дугу, равны.

2. Касательные к окружности, проведенные из одной точки, равны.

3. Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.

4. Из всех замкнутых кривых, для которых длины всех хорд не превосходят заданной величины, окружность ограничивает область максимальной площади.

5. Любые две дуги окружности равной длины можно совместить.

Это свойство называется самоконгруэнтностью. На плоскости им, кроме окружности, обладает только прямая. Если кривая может не лежать в плоскости, оно задает также винтовую линию.

Однако замкнутых самоконгруэнтных кривых, отличных от окружности, не существует. Благодаря этому свойству меч, имеющий форму дуги окружности, можно вставлять и вынимать из ножен той же формы.

6. При любом расположении двух равных окружностей на плоскости они имеют не больше двух общих точек.

7. Любая прямая, проходящая через центр окружности, является ее осью симметрии.

Для некоторых из перечисленных свойств доказательства того, что они определяют окружность, а значит являются ее признаками, совсем элементарны. Для других, напротив, весьма сложны. Наиболее интересны доказательства признаков 2 и 6. (Попробуйте найти их самостоятельно; если не получится – смотрите ниже.)

А теперь приведем два красивых свойства окружности, которыми обладают и другие кривые.

«Не уникальные» свойства окружности

1. Окружность является кривой постоянной ширины.

Это значит, что если провести к окружности две параллельные касательные, то расстояние между ними не зависит от их направления.

Как ни странно, этим свойством обладают многие кривые, в том числе довольно сильно отличающиеся от окружности. Наиболее простая из них, так называемый треугольник Рело , изображена на следующем рисунке.

Он состоит из трех дуг окружностей, центры которых расположены в вершинах правильного треугольника, а радиусы равны его стороне. Если изготовить несколько катков, поперечные сечения которых являются кривыми постоянной ширины, то можно перевозить на них плоскую платформу, и она не будет перемещаться вверх и вниз.

Отметим также, что все кривые данной постоянной ширины имеют одну и ту же длину .

2. Любая прямая, которая делит пополам периметр окружности, делит пополам и площадь ограниченного ею круга.

Разумеется, помимо окружности этим свойством обладают любые кривые, имеющие центр симметрии. Гораздо интереснее то, что обладать им могут и не центрально-симметричные кривые, в том числе и выпуклые. Вот изображение одной из таких фигур:

Ее можно задать следующими уравнениями:

Доказательство признака 2

Пусть дана выпуклая гладкая кривая, касательные к которой из любой точки равны. Возьмем произвольную точку А вне кривой и проведем касательные АВ’ и АС’ . Докажем, что для всех точек А’ , лежащих на дуге В’С’ (одной и той же), углы В’А’С’ совпадают.

Проведем через А’ касательную к кривой и найдем точки В и С ее пересечения с АС’ и АВ’ .

По условию треугольники В’А’С’ и C’A’B’ равнобедренные, следовательно:

∠ C’A’B’ = π – ∠ BA’C’ – ∠ CA’B’ = ½ · (∠ CBA – ∠ ACB) = ½ · (π – ∠ BAC) .

Таким образом угол, под которым видна хорда В’С’ , не зависит от выбора точки на дуге. Для второй дуги доказательство аналогично. По первому признаку, из приведенных выше, кривая является окружностью.

Доказательство признака 6

Прежде всего, отметим, что в любую замкнутую кривую можно вписать правильный треугольник. Действительно, возьмем на кривой произвольную точку А и повернем кривую вокруг А на π /3. Точка пересечения старого и нового положения кривой, отличная от А будет второй вершиной треугольника.

Итак пусть правильный треугольник с центром О вписан в нашу кривую. Повернем ее вокруг О на угол 2 π /3. Старое и новое положение кривой пересекаются, по крайней мере, в трех точках (вершинах треугольника) и, значит, совпадают, т.е. О является центром симметрии 3 порядка. Рассмотрим теперь поворот кривой вокруг О на произвольный угол φ . Если старое и новое положение кривой не совпадают, то число точек их пересечения кратно 3 (в силу симметрии) и не равно 0 (иначе одна кривая лежала бы целиком внутри другой, что для конгруэнтных кривых невозможно). Следовательно, кривая переходит в себя при любом повороте вокруг О , т.е. является окружностью.

Источники: А. Заславский. Свойства и признаки окружности. («Квант», №6, 2001), Википедия.

Окружность

Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.

Часть плоскости, ограниченная окружностью называется кругом.

Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.

Видео:Доказательство замечательного свойства трапеции при помощи метода параллельной проекцииСкачать

Основные термины

Касательная

Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойства касательной

Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Хорда

Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.

Свойства хорд

Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

Дуги, заключенные между параллельными хордами, равны.

Если две хорды окружности, AB и CD пересекаются в точке M , то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Свойства окружности

Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку ( касательная ); иметь с ней две общие точки ( секущая ).
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на линии, соединяющей их центры.

Теорема о касательной и секущей

Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC 2 = MA•MB .

Теорема о секущих

Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Углы в окружности

Центральным углом в окружности называется плоский угол с вершиной в ее центре.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.

Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.

Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Свойства углов, связанных с окружностью

Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.

Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на диаметр, равен 90°.

Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Длины и площади

Длина окружности C радиуса R вычисляется по формуле:

Площадь S круга радиуса R вычисляется по формуле:

Длина дуги окружности L радиуса R с центральным углом ,измеренным в радианах, вычисляется по формуле:

Площадь S сектора радиуса R с центральным углом в радиан вычисляется по формуле:

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанные и описанные окружности

Окружность и треугольник

центр вписанной окружности — точка пересечения биссектристреугольника, ее радиус r вычисляется по формуле:

где S — площадь треугольника, а — полупериметр;

центр описанной окружности — точка пересечения серединных перпендикуляров, ее радиус R вычисляется по формуле:

здесь a, b, c — стороны треугольника, — угол, лежащий против стороны a , S — площадь треугольника;

центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы;

центр описанной и вписанной окружностей треугольника совпадают только в том случае, когда этот треугольник — правильный.

Окружность и четырехугольники

около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°:

в четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон:

около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником;
около трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная; центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне;
в параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.