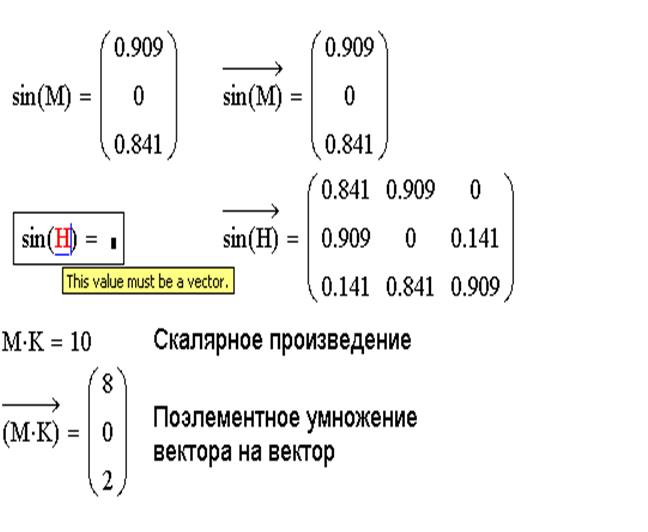
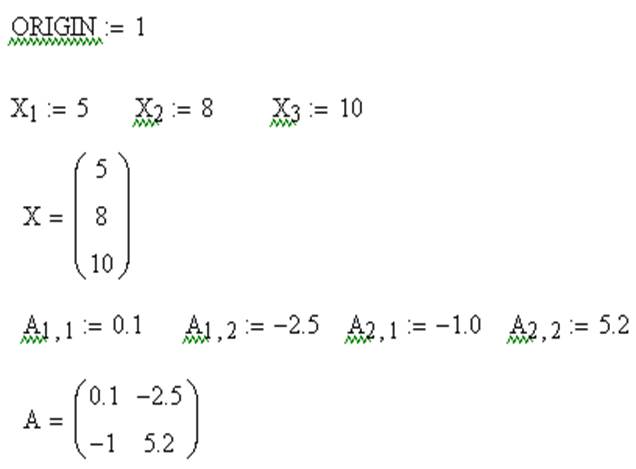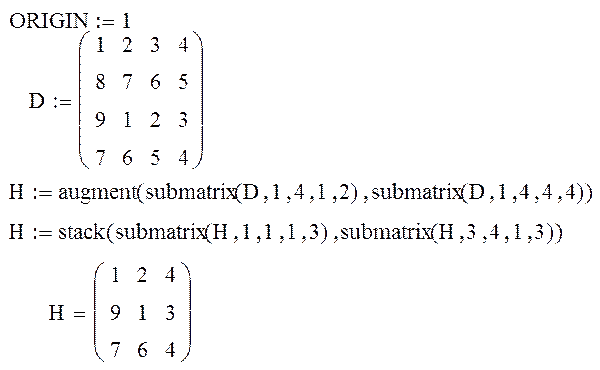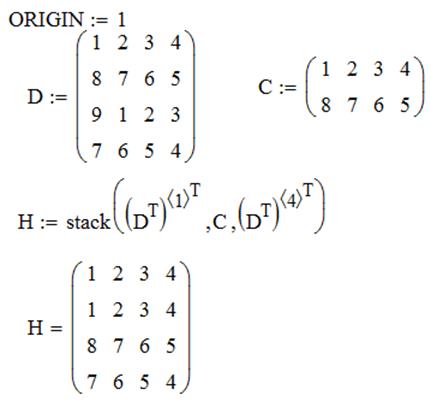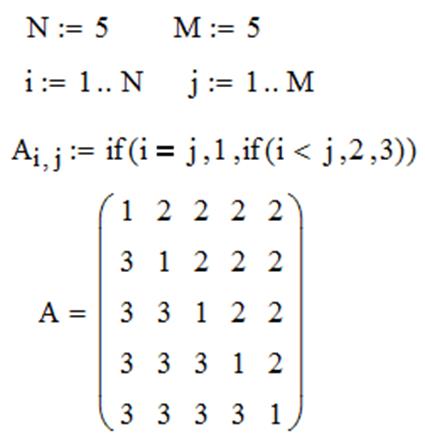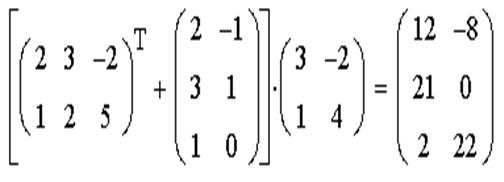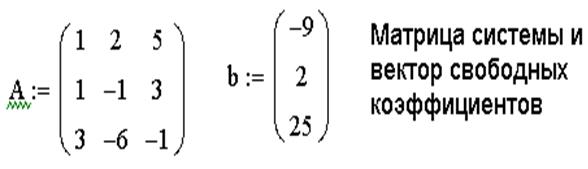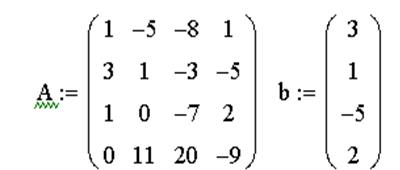Задать вектор случайных чисел mathcad (2 видео)

Задать вектор случайных чисел mathcad

Mathcad поставляется с рядом функций для генерирования случайных чисел, имеющих разнообразные распределения вероятностей. Функциональные формы распределений, связанных с приведенными ниже функциями даны в подразделе “Распределения вероятности”.

Mathcad PLUS поставляется со всеми функциями, перечисленными в этом разделе. Если Вы не используете Mathcad PLUS, Вы будете иметь все генераторы случайных чисел, связанные со следующими законами распределения вероятностей: нормальным, хи-квадрат, t-распределением Стьюдента, F, биномиальным, Пуассона и равномерным.

Е rbeta (m, s₁, s₂)	Возвращает вектор m случайных чисел, имеющих бэта-распределение. s₁, s₂ > 0 есть параметры формы.
rbinom (m, n, p)	Возвращает вектор m случайных чисел, имеющих биномиальное распределение. 0 p 1. n есть натуральное число.
Е rcauchy (m, l, s)	Возвращает вектор m случайных чисел, имеющих распределение Коши. s > 0 есть параметр масштаба. l — параметр расположения.
rchisq (m, d)	Возвращает вектор m случайных чисел, имеющих распределение хи-квадрат. d > 0 есть число степеней свободы.
Е rexp (m, r)	Возвращает вектор m случайных чисел, имеющих экспоненциальное распределение. r > 0 — параметр распределения.
rF (m, d₁, d₂)	Возвращает вектор m случайных чисел, имеющих F -распределение. d₁, d₂ > 0 есть числа степеней свободы.
Е rgamma (m, s)	Возвращает вектор m случайных чисел, имеющих гамма- распределение, s > 0 есть параметр формы.
Е rgeom (m, p)	Возвращает вектор m случайных чисел, имеющих геометрическое распределение. 0 Е rlnorm (m, m , s )	Возвращает вектор m случайных чисел, имеющих логнормальное распределение, в котором m я вляется натуральным логарифмом среднего значения, а s > 0 есть натуральный логарифм среднеквадратичного отклонения.
Е rlogis (m, l, s)	Возвращает вектор m случайных чисел, имеющих логистическое распределение, в котором l является п а раметром расположения, а s > 0 есть параметр масштаба.
Е rnbinom (m, n, p)	Возвращает вектор m случайных чисел, имеющих отрицательное биномиальное распределение. 0 m , s )	Возвращает вектор m случайных чисел, имеющих нормальное распределение. s > 0.
rpois (m, l )	Возвращает вектор m случайных чисел, имеющих распределение Пуассона. l > 0.
rt (m, d)	Возвращает вектор m случайных чисел, имеющих t-распределение Стьюдента. d > 0.
runif (m, a, b)	Возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором b и a являются граничными точками интервала. a Е rweibull (m, s)	Возвращает вектор m случайных чисел, имеющих распределение Вейбулла, в котором s > 0 является параметром формы.

Каждый раз, когда повторно вычисляется выражение, содержащее одну из этих функций, Mathcad генерирует новые случайные числа. Чтобы заставить Mathcad генерировать новые случайные числа, щёлкните мышью на выражении, содержащем функцию, и нажмите [F9]. Рисунок 3 показывает пример того, как использовать генератор случайных чисел Mathcad. Рисунок 4 показывает, как создать большой вектор случайных чисел, имеющих заданное распределение.

Каждая из этих функций в действительности создаёт последовательность псевдослучайных чисел, связанную с некоторым задаваемым стартовым значением. Каждое нажатие [F9] заставляет функцию выдать новое значение из этой последовательности. Одно и то же стартовое значение производит одинаковые последовательности чисел. Изменение стартового значения приводит к смене последовательности случайных чисел, выдаваемых функцией.

Чтобы изменить стартовое значение, выберите Генератор случайных чисел. из меню Математика и измените стартовое значение в диалоговом окне. Убедитесь, что введено целое число.

Чтобы перезапустить генератор случайных чисел Mathcad, не изменяя стартового значения, выберите Генератор случайных чисел. из меню Математика и нажмите “OK”, чтобы принять текущее значение. Затем щёлкните мышью на выражении с функцией, генерирующей случайное число, и нажмите [F9].

Рисунок 3: Равномерно распределенные случайные числа. Так как генератор случайных чисел производит каждый раз различные числа, маловероятно, что удастся в точности воспроизвести этот пример.

Рисунок 4: Вектор случайных чисел, распределенных по нормальному закону.

Так как генератор случайных чисел был сброшен, Mathcad будет производить те же самые случайные числа, которые производились бы после перезапуска Mathcad.

Если нужно несколько раз использовать одну и ту же последовательность случайных чисел, сбросьте генератор случайных чисел между вычислениями, как описано выше.

Чтобы получить новый набор случайных чисел, измените стартовое значение, как описано выше. Это заставит Mathcad генерировать набор случайных чисел, отличный от того, который создаётся после перезапуска Mathcad. Каждый раз при необходимости получить новую последовательность случайных чисел следует переустанавливать стартовое значение, как описано выше.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Создание матриц в MathCAD 14 (18/34)Скачать

Задать вектор случайных чисел mathcad

Глава 7. Математическая статистика

7.3 Генераторы случайных чисел

Для каждого закона распределения в MathCAD имеется функция-генератор случайных чисел, что позволяет выполнять моделирование методами Монте – Карло. Простейшая из них, функция rnd ( N ), возвращает одно случайное число, лежащее в интервале от 0 до N . Все другие функции-генераторы случайных чисел создают вектор чисел, распределенных по выбранному закону. Например, runif ( M , a , b ) создает вектор из М чисел, равномерно распределенных в интервале от a до b . Примеры работы генератора случайных чисел приведены на рис. 7.7 и 7.8.

создать одно случайное число, равномерно распределенное между 0 и х

(сотрите знак равенства и введите его вновь — число поменяется) rnd(x)

одно число вектор

Опустите вниз оно из выражений V

сортировка вектора по росту и обратно

среднее арифметическое

дисперсия

среднее квадратическое отклонение

медиана

Рис. 7.7 Работа генератора случайных чисел

Формирование массива случайных чисел

Для всех функций, кроме rnd

поменяйте генератор

Для функции rnd

Рис. 7.8 Работа генератора случайных чисел (продолжение)

Видео:Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать

Векторы и матрицы в MathCAD

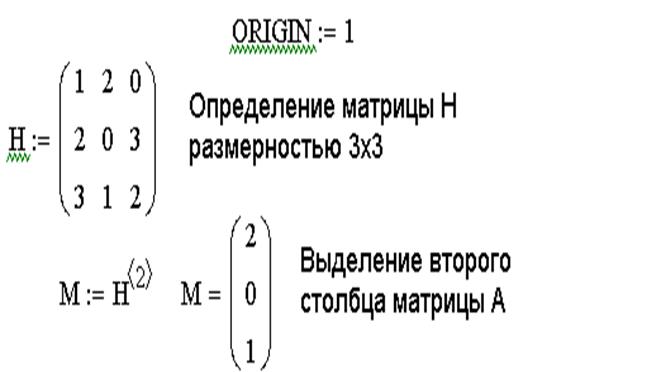
Нижняя граница индексации в MathCAD определена системной переменной ORIGIN. По умолчанию ORIGIN=0. Значение переменной можно переопределить. Например, ORIGIN=1.

Векторы и матрицы в MathCAD можно задавать путем ввода их элементов. Для ввода индекса элемента массива используется символ – [.

Поэлементный ввод массива Х

Вводимые символы	Отображаемые символы
X [ 1 Shift+: 5	X₁:=5
X [ 2 Shift+: 8	X₂:= 8
X [ 3 Shift+: 10	X₃:= 10

Поэлементный ввод матрицы А

Вводимые символы	Отображаемые символы
A [ 1,1 Shift+: 0.1	A₁₁ := 0.1
A [ 1,2 Shift+: -2.5	A₁₂ := -2.5
A [ 2,1 Shift+: -1.0	A₂₁ := -1.0
A [ 2,2 Shift+: 5.2	A₂₂ := 5.2

Для операций с матрицами и векторами предназначена панель Matrix, которая открывается щелчком по кнопке в панели математических инструментов.

ПанельMatrix содержит следующие кнопки:

– определение размеров матрицы;

– ввод элемента массива ;

– вычисление матрицы, обратной к данной ;

– вычисление определителя матрицы ;

– оператор векторизации (поэлементные операции с векторами и матрицами) ;

– определение столбца матрицы ;

– транспонирование матрицы ;

– определение ранжированной переменной;

– вычисление скалярного произведения векторов;

– вычисление векторного произведения векторов;

– вычисление суммы компонент вектора.

– визуализация цифровой информации.

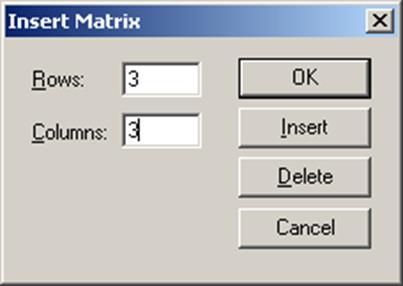
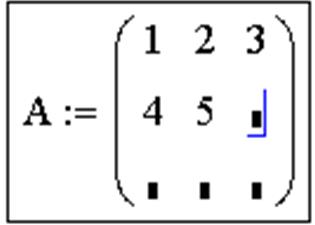
Действия, которые необходимо выполнить, чтобы ввести матрицу в рабочий документ при помощи кнопки панели Matrix:

1. Ввести с клавиатуры имя матрицы и знак присваивания;

2. Щелчком по кнопке открыть окно диалога:

3. Определить число строк (Rows) и число столбцов (Columns) будущей матрицы;

4. Закрыть окно диалога, щелкнув по кнопке OK;

5. Ввести элементы матрицы, установив курсор в поле ввода, которое появится справа от знака присваивания:

Функции определения матриц и операции с блоками матриц:

matrix(m,n,f) – создает и заполняет матрицу A=<a_ij> размерности m на n, каждый элемент которой a_ij равен значению функции f(i,j);

diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;

identity(n) – создает единичную матрицу порядка n;

augment(A,B) – из матриц А и В формируется третья матрица, первые столбцыкоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число строк);

stack(A,B) – из матриц А и В формируется третья матрица, первые строкикоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число столбцов);

submatrix(A,l,k,p,r) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с l по k и в столбцах с p по r (l T , где А — квадратная, симметричная, положительно определенная матрица, L – треугольная матрица;

sort(v) – сортировка элементов вектора v в порядке возрастания их значений;

reverse(v) – перестановка элементов вектора v в обратном порядке;

csort(A,n) – перестановка строк матрицы А таким образом, чтобы отсортированным оказался n-й столбец;

rsort(A,n) – перестановка столбцов матрицы А таким образом, чтобы отсортированной оказалась n-я строка.

ЗАДАЧА 1. Сформировать матрицу H из элементов матрицы D, исключив третий столбец и вторую строку.

ЗАДАЧА 2. Сформировать матрицу H следующим образом. Первая и последняя строки равны строкам матрицы D, остальные совпадают с матрицей C.

ЗАДАЧА 3. Сформировать матрицу таким образом, чтобы элементы на главной диагонали были равны 1, выше главной диагонали – 2, а ниже – 3.

ЗАДАЧА 4. Элементы матрицы формируются по формуле 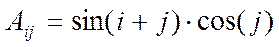. Сформировать вектор из максимальных элементов столбцов матрицы А. Найти сумму элементов матрицы, расположенных в четных строках.

ЗАДАЧА 5. Выполнить действия над матрицами А, В, С:

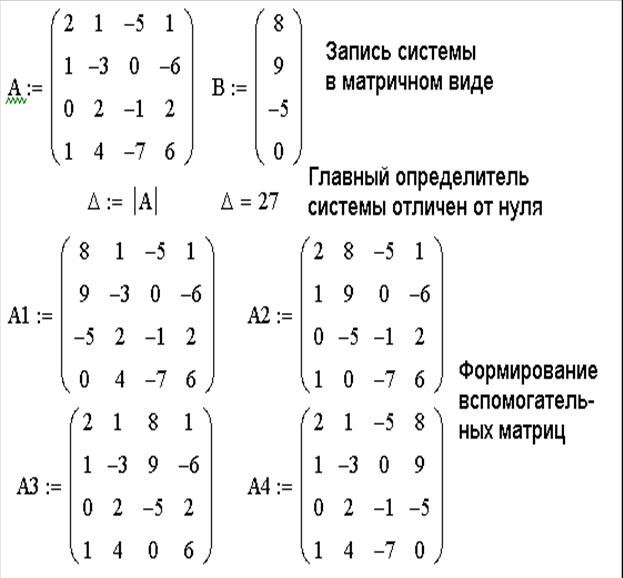
ЗАДАЧА 6. Решить систему линейных уравнений при помощи правила Крамера:

Для решения поставленной задачи необходимо выполнить следующие действия:

1. Сформировать матрицу системы А и вектор правых частей b.

2. Вычислить главный определитель ∆.

3. Сформировать вспомогательные матрицы (удобно скопировать матрицу А несколько раз и последовательно заменять в ней столбцы на вектор b) для вычисления определителей ∆_i;

4. Вычислить определители ∆_i;

5. Найти решение системы по формуле x_i=∆_i/∆.

ЗАДАЧА 7. Решить систему линейных уравнений методом обратной матрицы.

1. Сформировать матрицу коэффициентов и вектор свободных членов системы.

2. Решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы и вектора свободных членов.

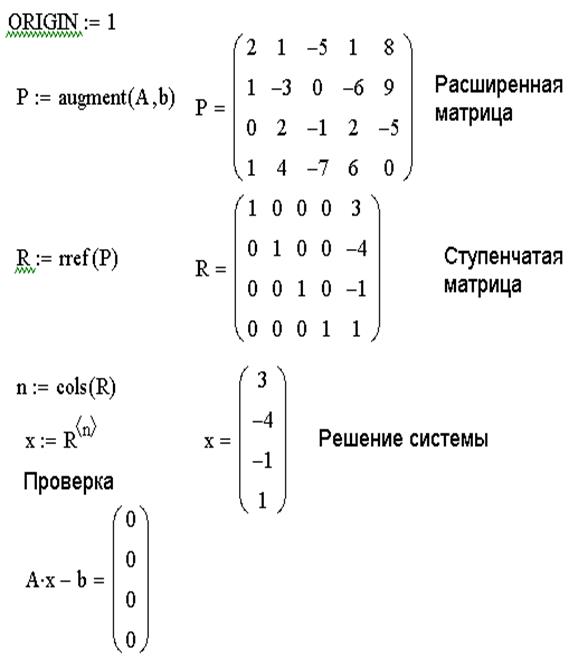
ЗАДАЧА 8. Решить систему линейных уравнений методом Гаусса.

Порядок решения задачи:

1. Сформировать матрицу коэффициентов и вектор свободных членов заданной системы.

2. Сформировать расширенную матрицу системы при помощи функции augment(A,b);

3. Используя функцию rref(A), привести расширенную матрицу к ступенчатому виду.

4. Получить решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте.

5. Выполнить проверку Ax-B=0.

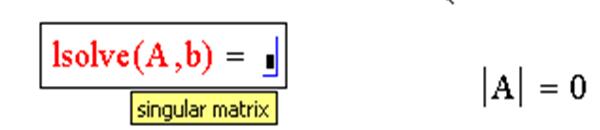
ЗАДАЧА 9. Решить систему при помощи функции lsolve:

Пример системы, которая не имеет решений:

Пример системы, которая имеет бесконечное множество решений

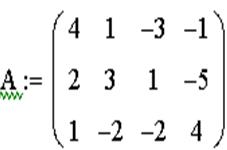
ЗАДАЧА 10. Решить систему при помощи решающего блока.

Решающий блок начинается с ключевого слова Given (Дано), которое необходимо ввести с клавиатуры.

Правее и ниже ключевого слова записываются уравнения системы.

Знак равенства в уравнениях вводится при помощи клавиш Ctrl+= или выбирается на панели инструментов Boolean.

Правее и ниже последнего уравнения системы вводится функция Find(x1,x2,…xn) (Найти), в скобках перечисляются имена переменных, значения которых нужно найти.

Численное решение системы можно получить, поставив знак равенства после функции Find(x1,x2,…xn).

Символьное решение получится, если после функции Find(x1,x2,…xn) указать знак стрелки, который находится в панели инструментов Symbolic (Ctrl+.).